COMPUTER SECURITY UNIT5 BASE NUMBER THEORY PUBLIC KEY

COMPUTER SECURITY UNIT-5: BASE NUMBER THEORY, PUBLIC KEY ENCRYPTION, RSA 1

INTRODUCTION TO NUMBER THEORY Modular Arithmetic Given any positive integer n and any integer a, if we divide a by n, we get an integer quotient q and an integer remainder r that obey the following relationship: a = qn + r Example: a = 11; a = -11; n = 7; 2 11 = 1 * 7 + 4; -11 = (-2) * 7 + 3; r=4 r=3

INTRODUCTION TO NUMBER THEORY Two integers a and b are said to be congruent modulo n, if (a mod n) = (b mod n) This is written as a ≡ b mod n Example: a = 23, b = 8, n = 5 23 mod 5 = 8 mod 5 We can write for the formula 23 ≡ 8 mod 5 3

Properties of the Modulo Operator The modulo operator have the following properties: a ≡ b mod n if n| (a-b). a ≡ b mod n implies b ≡ a mod n. a ≡ b mod n and b ≡ c mod n imply a ≡ c mod n. Example: a ≡ b mod n if n|a-b 23 ≡ 8 mod 5 �(23 -8)/5 = 15/5 = 3 a ≡ b mod n if (a-b/n) � a mod n �b mod n 4

Example: 23 ≡ 8 mod 5 if (23 -8)/5 23 mod 5 ≡ 8 mod 5 if 15/5 3 3 3 Example 2: a ≡ b mod n implies b ≡ a mod n � a mod n ≡ b � b ≡ a mod n 5
![Modular arithmetic exhibits the following properties: 1. [(a mod n) + (b mod n)] Modular arithmetic exhibits the following properties: 1. [(a mod n) + (b mod n)]](http://slidetodoc.com/presentation_image_h2/ec9cb39591b4d48158b8fa58467f145c/image-6.jpg)
Modular arithmetic exhibits the following properties: 1. [(a mod n) + (b mod n)] mod n = (a + b) mod n 2. [(a mod n) - (b mod n)] mod n = (a - b) mod n 3. [(a mod n) * (b mod n)] mod n = (a * b) mod n Examples of the three properties: Ex: 11 mod 8 = 3; 15 mod 8 = 7 1. [(11 mod 8) + (15 mod 8)] mod 8 = (11 + 15) mod 8 2. [(11 mod 8) (15 mod 8)] mod 8 = (11 15) mod 8 3. [(11 mod 8) (15 mod 8)] mod 8 = (11 15) mod 8 6

we demonstrate the first property. Define (a mod n) = ra and (b mod n) = rb. Then we can write a = ra + jn for some integer j and b = rb + kn for some integer k. Then (a + b) mod n = (ra + jn + rb + kn) mod n = (ra + rb + (k + j)n) mod n = (ra + rb) mod n = [(a mod n) + (b mod n)] mod n 7

Define the set Zn as the set of nonnegative integers less than n: Zn = {0, 1… (n-1)} This is referred to as the set of residues, or residue classes modulo n. to be more precise, each integer in Zn represents a residue class. However, if we take a = 5 and n = 8, whose only common factor is 1, Z 8 0 1 2 3 4 5 6 7 Multiply by 5 0 5 10 15 20 25 30 35 Residues 0 5 2 7 4 1 6 3 The line of residues contains all the integers in Z 8, in a different order. 8

Euclid’s Algorithm One of the basic techniques of number theory is Euclid’s algorithm, which is a simple procedure for determining the greatest common divisor of two positive integers. Greatest Common Divisor We will use the notation gcd(a, b) to mean the greatest common divisor of a and b. Definition is the following: gcd(a, b) = max[k, such that k|a and k|b] gcd(60, 24) = 12 9

also, because all nonzero integers divide 0, we have gcd(a, 0) = |a|. we stated that two integers a and b are relatively prime if their only common positive integer factor is 1. This is equivalent to saying that a and b are relatively prime if gcd(a, b) = 1. 10

8 and 15 are Relatively Prime because the positive divisors of 8 are 1, 2, 4, and 8, and the positive divisors of 15 are 1, 3, 5, and 15, so 1 is the only integer on both lists. 11

Finding the Greatest Common Divisor ( GCD ) Euclid’s algorithm is based on the following theorem: for any nonnegative integer a and any positive integer b, gcd(a, b) = gcd(b, a mod b) ---- (1) gcd(55, 22) = gcd(22, 55 mod 22) = gcd(22, 11) = 11 Euclid’s algorithm made repeated use of Equation (1) to determine the greatest common divisor, as follows. The algorithm assumes a > b > 0. It is acceptable to restrict the algorithm to positive integers because gcd(a, b) = gcd(|a|, |b|). 12

EUCLID(a, b) 1. A �a; B �b 2. if B = 0 3. R = A mod B 4. A �B 5. B �R 6. goto step 2 13 return a

It is easy to determine the greatest common divisor of two positive integers if we express each integer as the product of power of primes. 300 = 22 * 31 * 52 18 = 21 * 32 gcd(18, 300) = 21 * 31 * 50 = 6 14

Two theorems that play important roles in public-key cryptography are Fermat’s theorem and Euler’s theorem. 1. Fermat’s Theorem Fermat’s theorem states the following: If p is prime and a is a positive integer not divisible by p, then ap-1 ≡ 1 mod p ……………. 15 (1)

Proof: From the above, we know that if all of the elements of Zp, where Zp is the set of integers {0, 1… p-1}, are multiplied by a, modulo p, the result consists of all of the elements of Z p in some sequence. Then {a mod p, 2 a mod p, 3 a mod p, …, (p-1)a mod p} = {1, 2… p-1} (in some order) multiplying the numbers in both sets (a mod p) * (2 a mod p) * …*((p-1) a mod p) = 1*2*3* … * (p-1) taking mod p on both sides [ (a mod p) * (2 a mod p) * …*((p-1) a mod p)] mod p = [1*2*3* … * (p-1)] mod p 16
![now from the rule [(a mod p) * (b mod p)] mod p = now from the rule [(a mod p) * (b mod p)] mod p =](http://slidetodoc.com/presentation_image_h2/ec9cb39591b4d48158b8fa58467f145c/image-17.jpg)
now from the rule [(a mod p) * (b mod p)] mod p = (a * b) mod p we can write it as [a*2 a*3 a* … *(p-1)a] mod p = [1*2* … *(p-1)] mod p ap-1 (p-1)! ≡ (p-1)! mod p ap-1 ≡ 1 mod p [we cancel (p-1)! on both sides according to the formula if a * b ≡ a*c mod n then b ≡ c mod n if a is relatively prime to n. ] An alternative form of theorem is also useful: if p is prime and a is any positive integer then ap ≡ a mod p 17

p a ≡ a mod p P = 5, a = 3, 35 = 243 ≡ 3 mod 5 P = 5, a = 10, 105 = 100000 ≡ 10 mod 5 ≡ 0 mod 5 Example: a = 7, p = 19 72 = 49 ≡ 11 mod 19 [try to write it in mod 19 format] 4 2 2 7 = 7 * 7 = 49 * 49 ≡ 11 mod 19 * 11 mod 19 ≡ 11 * 11 mod 19 ≡ 121 mod 19 ≡ 7 mod 19 8 4 4 7 = 7 * 7 ≡ 7 mod 19 * 7 mod 19 ≡ 49 mod 19 ≡ 11 mod 19 716 = 78 * 78 ≡ 11 mod 19 * 11 mod 19 ≡ 11 *11 mod 19 ≡ 121 mod 19 ≡ 7 mod 19 18 16 2 7 = 7 * 7 ≡ 7 mod 19 * 11 mod 19 ≡ 77 mod 19 ≡ 1 mod 19 � 718 ≡ 1 mod 19 �ap-1 ≡ 1 mod p 18 [from formula]

Euler’s Totient Function Calculate relatively prime numbers below the given number. n-number, Φ(n) –Relatively primes below the n. If n is a prime number, Φ(n) = n-1. If n is not a prime number Φ(n) = Φ(pq) [here p, q are prime numbers] Φ(n) = (p-1) * (q-1) Determine Φ(37) and Because 37 is prime all of the +ve integers from 1 to 36 are relatively prime to 37. Thus Φ(37) = 36. 19

To determine Φ(35), we list all of the positive integers less than 35 that are relatively prime to it. 1, 2, 3, 4, 6, 8, 9, 11, 12, 13, 16, 17, 18, 19, 22, 23, 24, 26, 27, 29, 31, 32, 33, 34. There are 24 numbers on the list, so Φ(35) = 24. Example: Φ(21) = (3 -1) * (7 -1) = 2 * 6 = 12 Where the 12 integers are {1, 2, 4, 5, 8, 10, 11, 13, 16, 17, 19, 20} 20

2 Euler’s theorem states that for every a and n that are relatively prime: aΦ(n) ≡ 1 mod n 21

Euler’s theorem states that for every a and n that are relatively prime: aΦ(n) ≡ 1 mod n Proof: The above equation is true if n is prime, because in that case Φ(n) = n-1 and Fermat’s theorem holds. however, it also holds for any integer n. Recall that Φ(n) is the number of +ve integers less than n that are relatively prime to n. Consider the set of such integers, labeled as follows: R = { x 1 , x 2 , … } 22

now multiply each element by a, modulo n: S = { (ax 1 mod n), (ax 2 mod n), … (a mod n) } = { x 1, x 2, … } (in some order) because a is relatively prime to n and xi is relatively prime to n. so, axi must also be relatively prime to n. Thus all the members of S are integers less than n that are relatively prime to n. Multiply both the set elements and take mod n then [(ax 1 mod n)*(ax 2 mod n)* … *a mod n)] mod n = [ x 1* x 2* …* ] mod n �[ax 1*ax 2* … *a ] mod n = [x 1* x 2* …* ] mod n �[ax 1*ax 2* … *a ] ≡ [x 1* x 2* …* ] mod n �aΦ(n) ≡ 1 mod n. 23

Example: a = 3; n = 10; aΦ(n) ≡ 1 mod n. 34 = 81 ≡ 1 mod 10 [here Φ(10) = 4] (2) a=2 n = 11 Φ(n) = (11 -1) = 10 210 = 1024 ≡ 1 mod 11 24

Public key cryptography 25
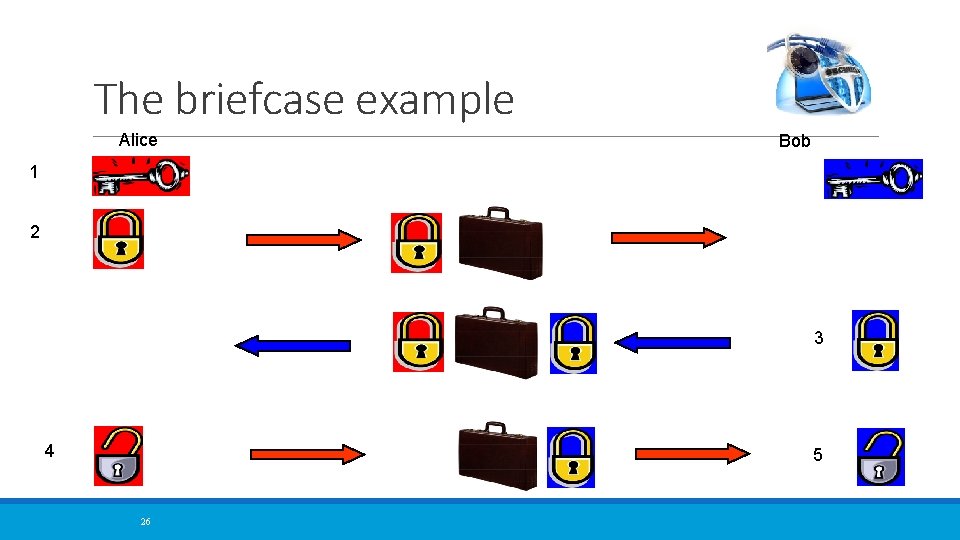
The briefcase example Alice Bob 1 2 3 4 5 26

The briefcase example Properties: 1. There is only one key for each padlock 2. The padlocks are so strong that they cannot be removed by force Problems: 3. You have no way of being sure that it is the correct person who finally gets your message 4. The briefcase has to be sent back and forward three times, which seems pretty inefficient. 27

Desirable properties Use the properties and problems for the briefcase example to come up with a specification of four properties that are desirable for any cipher system that is to be used between two entities who do not already share a symmetric key. 28

Public key blueprint The keys used to encrypt and decrypt are different. Anyone who wants to be a receiver needs to “publish” an encryption key, which is known as the public key. Anyone who wants to be a receiver needs a unique decryption key, which is known as the private key. It should not be possible to deduce the plaintext from knowledge of the ciphertext and the public key. Some guarantee needs to be offered of the authenticity of a public key. 29

Example A popular implementation of public-key encryption is the Secure Sockets Layer (SSL). Originally developed by Netscape, SSL is an Internet security protocol used by Internet browsers and Web servers to transmit sensitive information. SSL has become part of an overall security protocol known as Transport Layer Security (TLS). In your browser, you can tell when you are using a secure protocol, such as TLS, in a couple of different ways. You will notice that the "http" in the address line is replaced with "https, " and you should see a small padlock in the status bar at the bottom of the browser window. When you're accessing sensitive information, such as an online bank account or a payment transfer service like Pay. Pal or Google Checkout, chances are you'll see this type of format change and know your information will most likely pass along securely. TLS and its predecessor SSL make significant use of certificate authorities. Once your browser requests a secure page and adds the "s" onto "http, " the browser sends out the public key and the certificate, checking three things: 1) that the certificate comes from a trusted party; 2) that the certificate is currently valid; and 3) that the certificate has a relationship with the site from which it's coming. 30
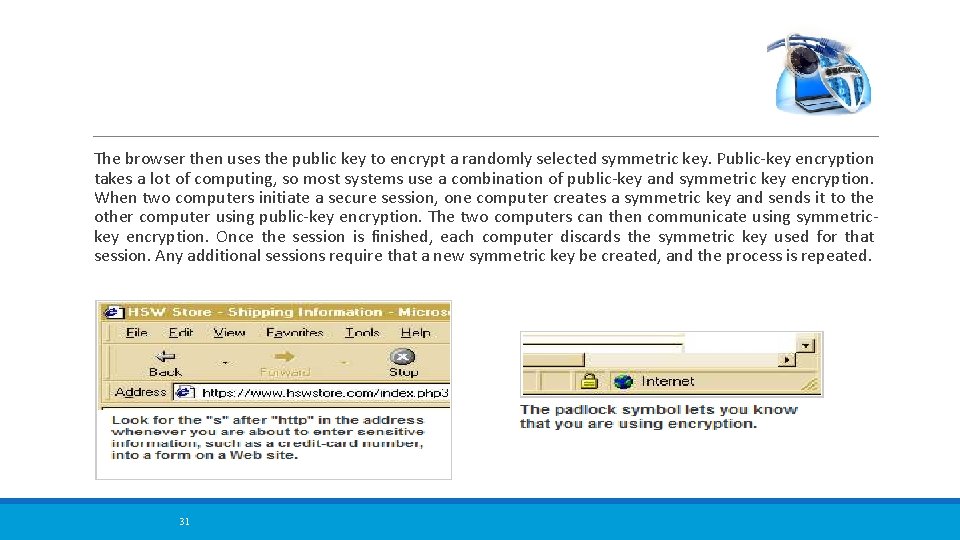
The browser then uses the public key to encrypt a randomly selected symmetric key. Public-key encryption takes a lot of computing, so most systems use a combination of public-key and symmetric key encryption. When two computers initiate a secure session, one computer creates a symmetric key and sends it to the other computer using public-key encryption. The two computers can then communicate using symmetrickey encryption. Once the session is finished, each computer discards the symmetric key used for that session. Any additional sessions require that a new symmetric key be created, and the process is repeated. 31

Design of a public key algorithm In a public key system, if everyone knows everything necessary: • the encryption algorithm and • the encryption key to determine the ciphertext then how is it possible that they cannot then work out what the plaintext (decryption key) is from this information? 32

One way functions A one-way function is a function that is “easy” to compute and “difficult” to reverse. How might we express this notion of a one way function informally in complexity theoretic terms? 33

OWF: Multiplying two primes It is easy to take two prime numbers and multiply them together. If they are fairly small we can do this in our heads, on a piece of paper, or on a calculator. As they get bigger and bigger it is fairly easy to write a computer program to compute the product. Multiplication runs in polynomial time. Multiplication of two primes is easy. 34

OWF: Multiplying two primes Multiplication of two prime numbers is believed to be a one-way function. We say believed because nobody has been able to prove that it is hard to factorise. Maybe one day someone will find a way of factorising efficiently. 35

OWF: Modular exponentiation The process of exponentiation just means raising numbers to a power. Raising a to the power b, normally denoted ab just means multiplying a by itself b times. In other words: ab = a x a x … x a Modular exponentiation means computing ab modulo some other number n. We tend to write this as ab mod n. Modular exponentiation is “easy”. 36

OWF: Modular exponentiation However, given a, b, and ab mod n (when n is prime), calculating b is regarded by mathematicians as a hard problem. This difficult problem is often referred to as the discrete logarithm problem. In other words, given a number a and a prime number n, the function f(b) = ab mod n is believed to be a one-way function. 37

Suitable OWFs We have seen that the encryption process of a public key cipher system requires a one way function. 38

RSA 39

RSA The RSA public key encryption algorithm was the first practical implementation of public key encryption discovered. It remains the most used public key encryption algorithm today. It is named after the three researchers Ron Rivest, Adi Shamir and Len Adleman who first published it. Make sure you are familiar with the concepts of modular arithmetic, prime numbers, the Euclidean Algorithm and the method of Repeated Squares. 40

Setting up RSA Let n be the product of two large primes p and q ◦ By “large” we typically mean at least 512 bits. Select a special number e ◦ greater than 1 and less than (p-1)(q-1). The precise mathematical property that e must have is that there must be no numbers that divide neatly into e and into (p-1)(q-1), except for 1. Publish the pair of numbers (n, e) Compute the private key d from p, q and e 41

Computing the private key The private key d is computed to be the unique inverse of e modulo (p-1)(q-1). In other words, d is the unique number less than (p-1)(q-1) that when multiplied by e gives you 1 modulo (p-1)(q-1). Written mathematically: ed = 1 mod (p-1)(q-1) The Euclidean Algorithm is the process that you need to follow in order to compute d. 42

Computing the private key 43 1. Who is capable of running the Euclidean Algorithm to find the private key? 2. How efficient is this process?

Choosing e Let’s consider p=3 and q=7. What choices of e are acceptable? In this case (p-1)(q-1) = 2 x 6 = 12. Any suitable choice of e must have the property that there are no numbers that neatly divide into e and 12 except for 1. Let’s just try them all out: e=2: this is no good, since 2 divides both e and 12. In fact this will be true for all multiples of 2 as well, so e=4, e=6, e=8 and e=10 are also not possible. e=3: this is no good, since 3 divides both e and 12. In fact this will be true for all multiples of 3 as well, so e=6 and e=9 are also not possible. The remaining choices are e=5, e=7 and e=11. Since in each case there is no number that divides into them and 12 other than 1, all these choices of e are possible. 44

Setting up RSA: example Step 1: Let p = 47 and q = 59. Thus n = 47 x 59 = 2773 Step 2: Select e = 17 Step 3: Publish (n, e) = (2773, 17) Step 4: (p-1) x (q-1) = 46 x 58 = 2668 Use the Euclidean Algorithm to compute the modular 2668. The result is d = 157 << Check: 17 x 157 = 2669 = 1(mod 2668) >> Public key is (2773, 17) Private key is 157 45 inverse of 17 modulo

Encryption and decryption The first job is to represent the plaintext as a series of numbers modulo n. The encryption process to obtain the ciphertext C from plaintext M is very simple: C = Me mod n The decryption process is also simple: M = Cd mod n 46

Encryption and decryption: example Public key is (2773, 17) Private key is 157 Plaintext block represented as a number: M = 31 Encryption using Public Key: C = 3117 (mod 2773) = 587 Decryption using Private Key: M = 587157 (mod 2773) = 31 47

Choose an integer e < n that is relatively prime to f(n). Find a second integer d such that ed mod f(n) = 1. The public key is (e, n), and the private key is d. Let m be a message. Then: c = me mod n and m = cd mod n 48

Example - RSA Let p = 7 and q = 11. Then n = 77 and f(n) = 60. Alice chooses e = 17, so her private key is d = 53. In this cryptosystem, each plaintext character is represented by a number between 00 (A) and 25 (Z); 26 represents a blank. Bob wants to send Alice the message "HELLO WORLD. " Using the representation above, the plaintext is 07 04 11 11 14 26 22 14 17 11 03. Using Alice's public key, the ciphertext is 0717 mod 77 = 28 0417 mod 77 = 16 1117 mod 77 = 44. . . 0317 mod 77 = 75 or 28 16 44 44 42 38 22 42 19 44 75. In addition to confidentiality, RSA can provide data and origin authentication. If Alice enciphers her message using her private key, anyone can read it, but if anyone alters it, the (altered) ciphertext cannot be deciphered correctly. 49

Example Suppose Alice wishes to send Bob the message "HELLO WORLD" in such a way that Bob will be sure that Alice sent it. She enciphers the message with her private key and sends it to Bob. As indicated above, the plaintext is represented as 07 04 11 11 14 26 22 14 17 11 03. Using Alice's private key, the ciphertext is 0753 mod 77 = 35 0453 mod 77 = 09 1153 mod 77 = 44. . . 0353 mod 77 = 05 or 35 09 44 44 93 12 24 94 04 05. In addition to origin authenticity, Bob can be sure that no letters were altered. ◦ Providing both confidentiality and authentication requires enciphering with the sender's private key and the recipient's public key. 50

Example: Suppose Alice wishes to send Bob the message "HELLO WORLD" in confidence and authenticated. Again, assume that Alice's private key is 53. Take Bob's public key to be 37 (making his private key 13). The plaintext is represented as 07 04 11 11 14 26 22 14 17 11 03. The encipherment is (0753 mod 77)37 mod 77 = 07 (0453 mod 77)37 mod 77 = 37 (1153 mod 77)37 mod 77 = 44. . . (0353 mod 77)37 mod 77 = 47 or 07 37 44 44 14 59 22 14 61 44 47. ◦ The recipient uses the recipient's private key to decipher the message and the sender's public key to authenticate it. 51

Example Bob receives the ciphertext above, 07 37 44 44 14 59 22 14 61 44 47. The decipherment is (0713 mod 77)17 mod 77 = 07 (3713 mod 77)17 mod 77 = 04 (4413 mod 77)17 mod 77 = 11. . . (4713 mod 77)17 mod 77 = 03 or 07 04 11 11 14 26 22 14 17 11 03. This corresponds to the meessage "HELLO WORLD" from the preceding example. 52

Security of RSA We will look at two different strategies for trying to “break” RSA: 1. Trying to decrypt a ciphertext without knowledge of the private key 2. Trying to determine the private key 53

Decrypting ciphertext without the key The encryption process in RSA involves computing the function C = Me mod n, which is regarded as being easy. An attacker who observes this ciphertext, and has knowledge of e and n, needs to try to work out what M is. Computing M from C, e and n is regarded as a hard problem. 54

RSA security summary There are two one-way functions involved in the security of RSA. One-way function Encryption function Multiplication of two primes 55 Description The encryption function is a trapdoor one-way function, whose trapdoor is the private key. The difficulty of reversing this function without the trapdoor knowledge is believed (but not known) to be as difficult as factoring. The difficulty of determining an RSA private key from an RSA public key is known to be equivalent to factoring n. An attacker thus cannot use knowledge of an RSA public key to determine an RSA private key unless they can factor n. Because multiplication of two primes is believed to be a one-way function, determining an RSA private key from an RSA public key is believed to be very difficult.
- Slides: 55