Computer Security Modular Arithmetic RSA Analysis SSLTLS Page

Computer Security Modular Arithmetic RSA Analysis SSL/TLS Page 1

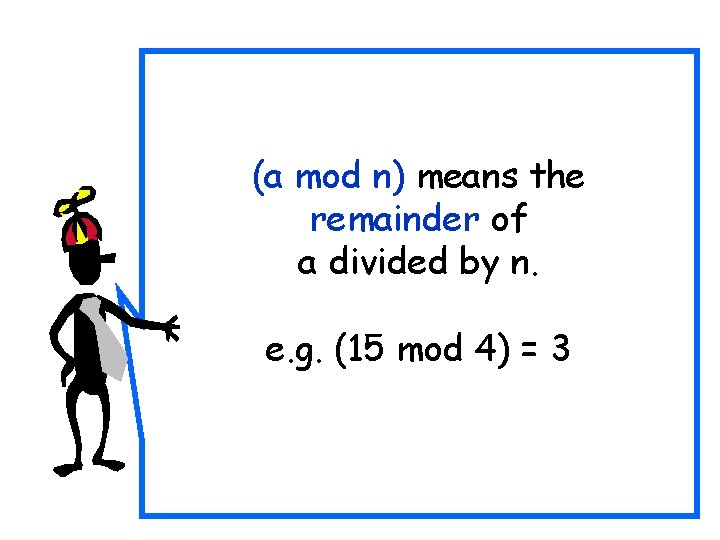
(a mod n) means the remainder of a divided by n. e. g. (15 mod 4) = 3

Definition: Modular equivalence of integers a and b a b [mod n] (a mod n) = (b mod n) a = b + kn for some integer k e. g. , 15 7 [mod 4] Also written as a n b, and spoken “a is congruent to b modulo n” or “a and b are equivalent modulo n”

n induces a natural partition of the integers into n classes. a and b are said to be in the same “residue class” or “congruence class” exactly when a n b.

Fundamental lemma of plus, minus, and times modulo n: If (x y) and (a n b). Then 1) x + a n y + b 2) x - a n y - b 3) x * a n y * b n

A Unique Representation System Modulo n: We pick exactly one representative from each residue class. We do all our calculations using these representatives.

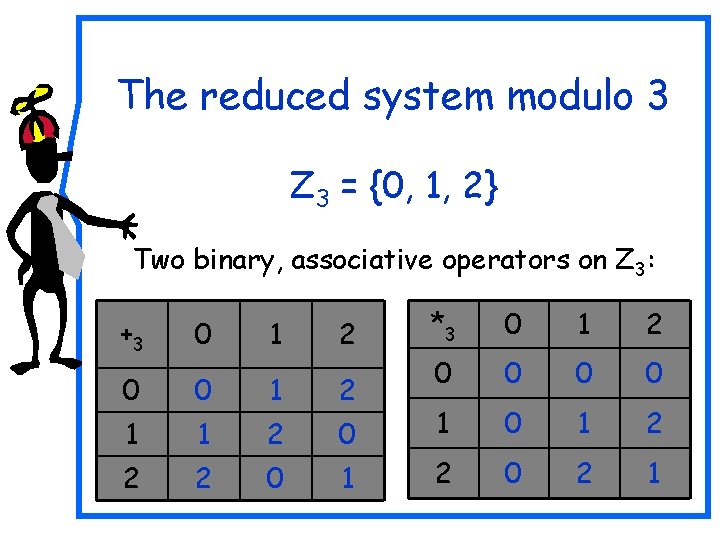
Perhaps the most convenient set of representatives: The reduced system modulo n: Zn = {0, 1, 2, …, n-1} Define operations +n and *n: a +n b = (a+b mod n) a *n b = (a*b mod n)

The reduced system modulo 3 Z 3 = {0, 1, 2} Two binary, associative operators on Z 3: 1 *3 0 1 2 0 0 0 1 2 1 2 0 2 1 +3 0 2 0 0 1 2 1 1 2 2 2 0

Is there a fundamental lemma of division modulo n? cx n cy x n y ? This statement holds if c has a multiplicative inverse. cx n cy c-1 cx n c-1 cy x n y

When doesn’t c have an inverse? If GCD(c, n) > 1 (i. e. , c shares a factor p>1 with n), then c does not have an inverse. c = k 1 p, n = k 2 p Proof by contradiction: Suppose that c has an inverse c-1. Then c*c-1= 1 + kn for some integer k. k 1 pc-1= 1 + kk 2 p p(k 1 c-1 -kk 2) = 1 But no multiple of p can be equal to 1.

Fundamental lemma of division modulo n. If GCD(c, n)=1, then ca n cb a n b Consider the set Zn* = {x Zn | GCD(x, n) =1} (multiplicative group of integers mod n) Multiplication over this set Zn* will have the cancellation property.

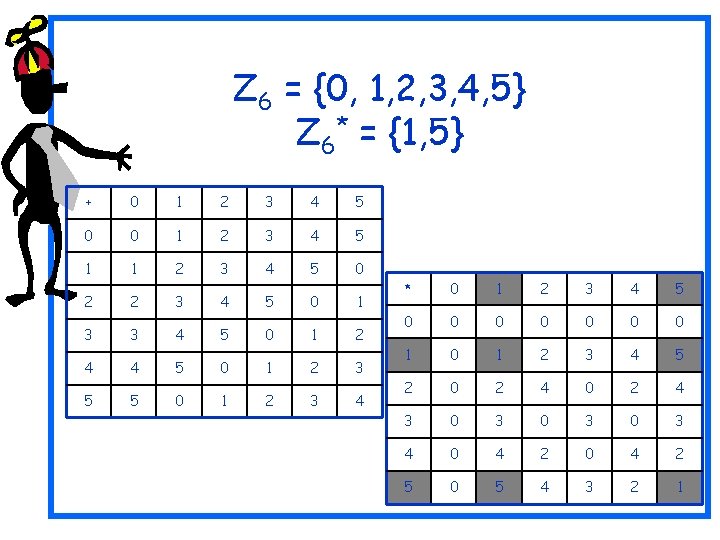
Z 6 = {0, 1, 2, 3, 4, 5} Z 6* = {1, 5} + 0 1 2 3 4 5 0 0 1 2 3 4 5 1 1 2 3 4 5 0 2 2 3 4 5 0 1 3 3 4 5 0 1 2 4 4 5 0 1 2 3 5 5 0 1 2 3 4 * 0 1 2 3 4 5 0 0 0 0 1 2 3 4 5 2 0 2 4 3 0 3 0 3 4 0 4 2 5 0 5 4 3 2 1

Z 12* = {0 ≤ x < 12 | gcd(x, 12) = 1} = {1, 5, 7, 11} *12 1 5 7 11 1 1 5 7 11 5 5 1 11 7 7 7 11 1 5 11 11 7 5 1

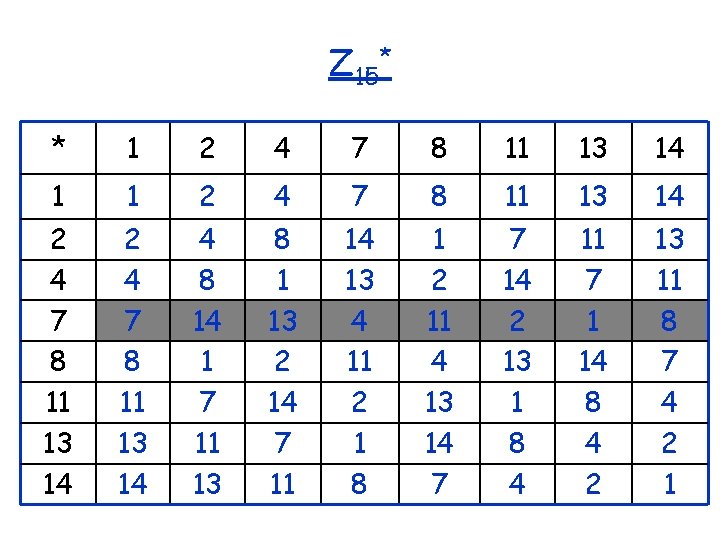
Z 15* * 1 2 4 7 8 11 13 14 1 1 2 4 7 8 11 13 14 4 8 14 1 7 11 13 8 1 13 2 14 7 11 14 13 4 11 2 1 8 1 2 11 4 13 14 7 7 14 2 13 1 8 4 11 7 1 14 8 4 2 13 11 8 7 4 2 1

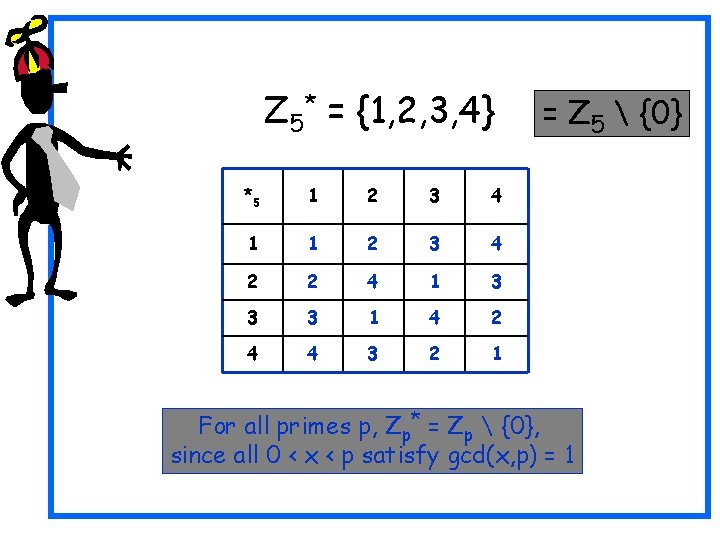
Z 5* = {1, 2, 3, 4} *5 1 2 3 4 1 1 2 3 4 2 2 4 1 3 3 3 1 4 2 4 4 3 2 1 = Z 5 {0} For all primes p, Zp* = Zp {0}, since all 0 < x < p satisfy gcd(x, p) = 1

Euler Phi Function (n) Define (n) = size of Zn* = number of 1 ≤ k < n that are relatively prime to n. p prime Zp*= {1, 2, 3, …, p-1} (p) = p-1

Z 12* = {0 ≤ x < 12 | gcd(x, 12) = 1} = {1, 5, 7, 11} (12) = 4 *12 1 5 7 11 1 1 5 7 11 5 5 1 11 7 7 7 11 1 5 11 11 7 5 1

Theorem: if p, q distinct primes then (pq) = (p-1)(q-1) pq = # of numbers from 1 to pq p = # of multiples of q up to pq q = # of multiples of p up to pq 1 = # of multiple of both p and q up to pq (pq) = pq – p – q + 1 = (p-1)(q-1)

Fundamental lemma of powers? If (a n b) Then xa n xb ? NO! (2 3 5) , but it is not the case that: 22 3 25 Notice that in xa, a is an integer indicating how many times to apply the multiplication operation, whereas x is an element in a multiplicative group. These are objects of different types.

Euler’s Theorem a Zn*, a (n) n 1 Fermat’s Little Theorem (special case) p prime, a Zp* ap-1 p 1

Fundamental lemma of powers. Suppose x Zn*, and a, b, n are naturals. If a (n) b Then xa n xb

RSA Invented by Rivest, Shamir and Adleman in 1978 Based on difficulty of factoring. Used to hide the size of a group Zn* since: Factoring has not been reduced to RSA – an algorithm that generates m from c does not give an efficient algorithm for factoring On the other hand, factoring has been reduced to finding the private-key. – there is an efficient algorithm for factoring given one that can find the private key. Page 23

RSA Public-key Cryptosystem What we need: • p and q, primes of approximately the same size • n = pq (n) = (p-1)(q-1) • e Z (n) • d = inv. of e in Z (n) i. e. , d = e-1 mod (n) Public Key: (e, n) Private Key: d Encode : m Zn E(m) = me mod n Decode : D(c) = cd mod n Page 24

RSA continued Why it works: D(c) = cd mod n = med mod n = m 1 + k(p-1)(q-1) mod n = m 1 + k (n) mod n = m(m (n))k mod n = m mod n =m (by Euler’s Theorem, if m and n are relatively prime, then m (n) mod n = 1 mod n) But wait… Page 25

What if m and n share a factor? Euler’s theorem doesn’t guarantee that mk (n) = 1 mod n Answer 1: It should be difficult to find an m that shares a factor with n, because this allows you to factor n using Euclid’s GCD algorithm! Answer 2: Special case, still works. Chinese Remainder Theorem: Suppose that n=pq, where p and q are relatively prime. Then for any integers a and b, there is a unique x (mod n) such that x = a mod p and x = b mod q. Special Case: If a=b, so that x = a mod p and x = a mod q, then x = a mod pq. Why? x = a mod pq satisfies both x = a mod p and x = a mod q, and there is only one such a! Page 26

What if m and n share a factor? Lemma: med = m mod p. If m = 0 mod p, then med = 0 = m mod p. Otherwise, if m ≠ 0 mod p, then where by Fermat’s Little Theorem mp− 1 = 1 mod p Similarly, med = m mod q. Therefore med = m mod pq CPS 290 Page 27

RSA computations To generate the keys, we need to – Find two primes p and q. Generate candidates and use primality testing to filter them. -1 e – Pick e such that GCD(e, (p-1)(q-1)) = 1. Find mod (p-1)(q-1)using Euclid’s algorithm. Takes time log 2(n) To encode and decode – Take me or cd. Use the power method. Takes time log(e) log 2(n) and log(d) log 2(n). In practice e is selected to be small so that encoding is fast. CPS 290 Page 28

Security of RSA Warning: – Do not use this or any other algorithm naively! Possible security holes: – Need to use “safe” primes p and q. In particular p 1 and q-1 should have large prime factors. – p and q should not have the same number of digits. Can use a middle attack starting at sqrt(n). – e cannot be too small – Don’t use same n for different e’s. – You should always “pad” CPS 290 Page 29

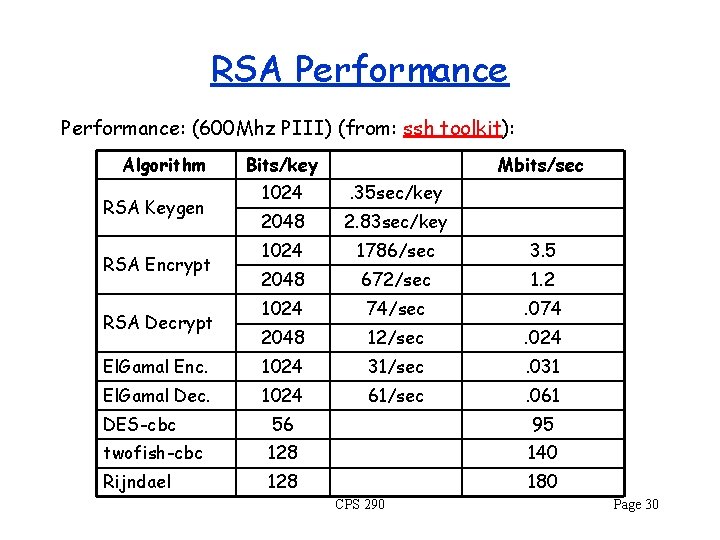
RSA Performance: (600 Mhz PIII) (from: ssh toolkit): Algorithm Bits/key Mbits/sec 1024 . 35 sec/key 2048 2. 83 sec/key 1024 1786/sec 3. 5 2048 672/sec 1. 2 1024 74/sec . 074 2048 12/sec . 024 El. Gamal Enc. 1024 31/sec . 031 El. Gamal Dec. 1024 61/sec . 061 RSA Keygen RSA Encrypt RSA Decrypt DES-cbc 56 95 twofish-cbc 128 140 Rijndael 128 180 CPS 290 Page 30

Factoring in the Real World Quadratic Sieve (QS): – Used in 1994 to factor a 129 digit (428 -bit) number. 1600 Machines, 8 months. Number field Sieve (NFS): – Used in 1999 to factor 155 digit (512 -bit) number. 35 CPU years. At least 4 x faster than QS – Used in 2003 -2005 to factor 200 digits (663 bits) 75 CPU years ($20 K prize) CPS 290 Page 31

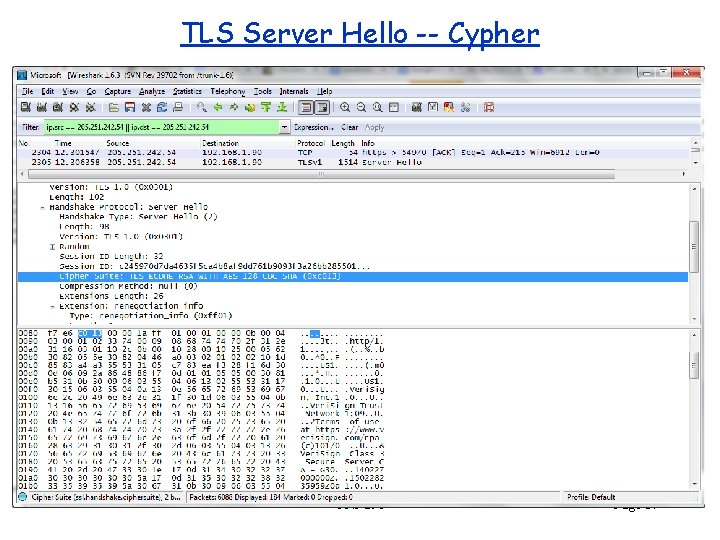
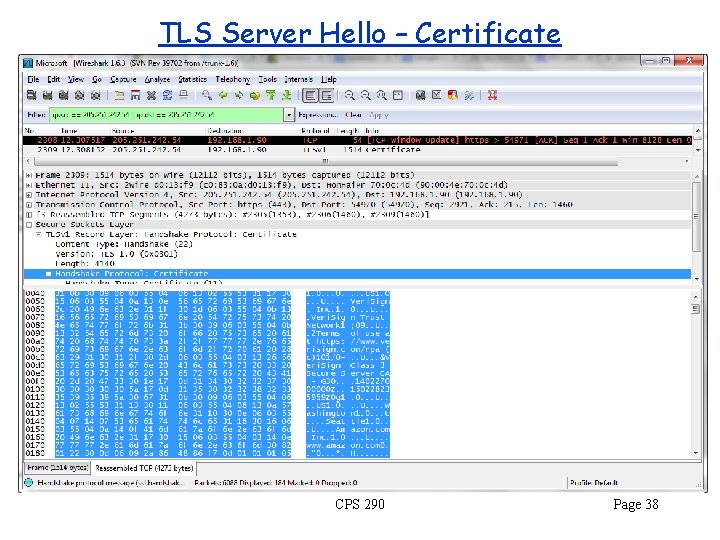
Example of SSL (3. 0) SSL (Secure Socket Layer) is the standard for the web (https ). Protocol (somewhat simplified): Bob -> amazon. com B->A: client hello: protocol version, acceptable Cipher. Suites A->B: server hello: Cipher. Suite, session ID, |amazon. com|verisign hand. B->A: key exchange, {masterkey}amazon’s public key A->B: server finish: ([amazon, prev-messages, masterkey])key 1 shake B->A: client finish : ([bob, prev-messages, masterkey])key 2 A->B: server message: (message 1, [message 1])key 1 data B->A: client message: (message 2, [message 2])key 2 |h|issuer = Certificate = Issuer, <h, h’s public key, time stamp>issuer’s private key <…>private key = Digital signature {…}public key = Public-key encryption [. . ] = Secure Hash (…)key = Private-key encryption key 1 and key 2 are derived from random masterkey and session ID CPS 290 Page 32

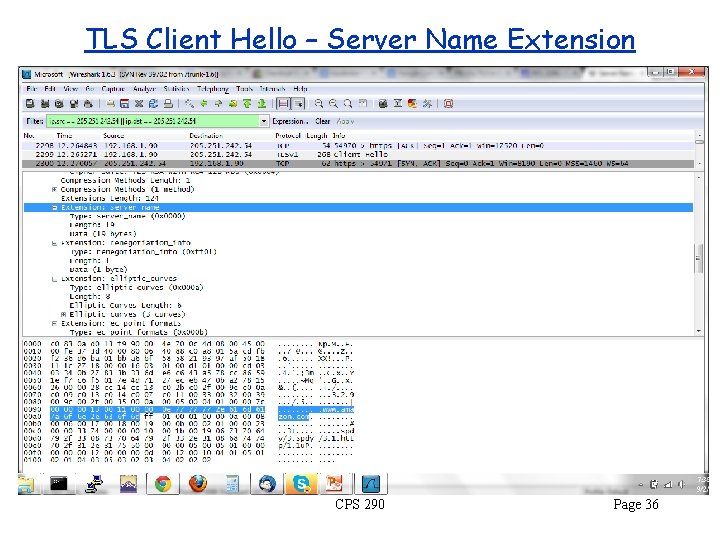
Server Name Issue The client expects the server to send a certificate matching the domain of the requested Web site. But the client doesn’t tell the server which Web site it is requesting -- not a problem if server hosts only one site. For servers hosting multiple secure Web sites, the “solution” is to assign multiple IP addresses to the network interface, one for each certificate. Akamai uses approximately 13 M IPv 4 addresses for this purpose. Better solution: “server name” extension in successor to SSL, TLS CPS 290 Page 33

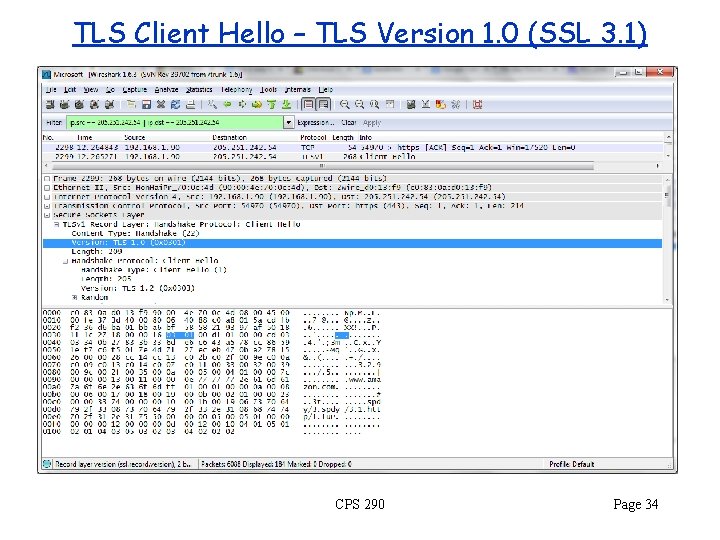
TLS Client Hello – TLS Version 1. 0 (SSL 3. 1) CPS 290 Page 34

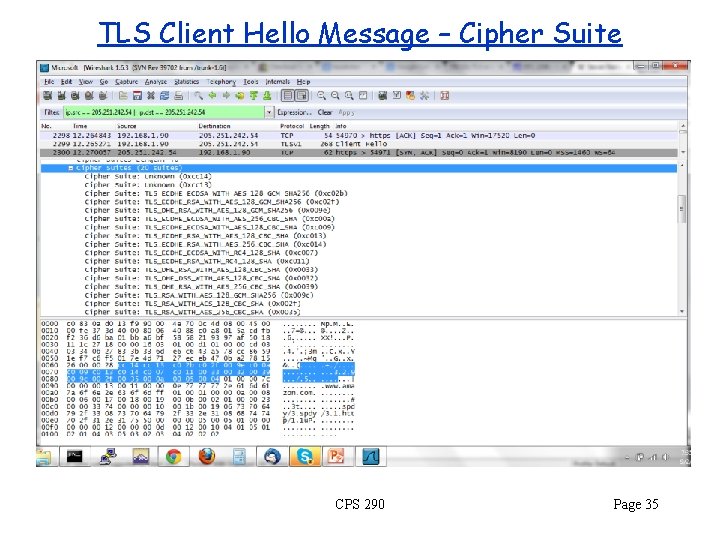
TLS Client Hello Message – Cipher Suite CPS 290 Page 35

TLS Client Hello – Server Name Extension CPS 290 Page 36

TLS Server Hello -- Cypher CPS 290 Page 37

TLS Server Hello – Certificate CPS 290 Page 38