Computer Security Key Management Introduction We distinguish between

Computer Security Key Management

Introduction We distinguish between a session key and a interchange key (long term key). The session key is associated with a session; the long term key with a principal.

Basic key exchange C = trusted third party • A C: {request for ksession for Bob}k. A • C A: {ksession}k. A, {ksession}k. B • A B: {ksession}k. B Now A and B share ksession.

Basic key exchange -- problems With whom is Bob sharing a key? Replay attacks: Eve may highjack a session.

Classical cryptography key exchange C = trusted third party • A C: { A||B|| rand 1 } • C A: { A||B||rand 1||ksession , {A ||ksession}k. B } k. A • A B: {A ||ksession}k. B • B A: {rand 2}ksession • A B: {rand 2 -1}ksession rand 1 and rand 2 are called nonces.

Classical cryptography key exchange Discussion on attacks. Intercept & highjack sessions, Use of Timestamps.

Kerberos Ticket : TAB = B || { A||A’s address||valid time||k. AB||t}k. B t is a timestamp, k. B is a key that B shares with an authentication server, AAB = { A||generation time}k. AB is an authenticator for A. 1. A C: A || B 2. C A: {k. AB}k. A || TAB 3. A B: G || AAB || TAB 4. B A: A || {k. AG}k. AB || TAG

Kerberos Discussion. How are principals (Alice, Bob) authenticated?

Key exchange with Public Key Cryptography First try. § A B: { ksession }e. B

Key exchange with Public Key Cryptography A fix § A B: A, { { ksession }d. A }e. B where d. A is the private key of A. Bob decrypts the received and uses the public key of A to obtain ksession from { ksession }d. A. But how does B get to know A’s key?

A man-in-the-middle attack The attacker E succeeds in convincing A that B’s public key is e. E and not e. B. . 1. A C: request for B’s public key – intercepted by E 2. E C: request for B’s public key 3. C E: e. B 4. E A: e. E 5. A B: {ksession}e. E -- intercepted by E 6. E B: {k }e

Public Key Infrastructures the X. 509 Authentication Framework X. 509 is based on certificate signature chains. Certificates are digitally signed by Certifying authorities and link a Public key to its owner. See textbook for details on X. 509 v 3 certificates.

Public Key Infrastructures Certificate signature chains Let X<<Y>> represent a certificate that X generated for the subject Y, eg X authenticated (digitally signed) the Public Key of Y. X<<Y>> represents the explicit trust that X has in (the public key of) Y (he wouldn’t otherwise certify it!).

Public Key Infrastructures Certificate signature chains A certificate chain: X 1<< X 2 >> || X 2<< X 3 >> ||. . . || Xn-1<< Xn >> represents the implicit trust of X 1 in Xn: X 1 trusts X 2, who in turn trusts X 3, . . . , and Xn-1 trusts Xn. PKI’s are based on implicit trust.

The structure of a PKI trust graphs A PKI is determined by its: § Certifying Authorities (CAs) § Subjects § Implicit trust relationships. The trust graph of a PKI is the graph whose nodes are the CAs and the subjects and whose edges are the explicit trust relationships. Implicit trust relationships are represented by paths

The structure of a PKI Trust graphs § The trust graph for the X. 509 PKI is essentially a graph tree, with leafs the subjects. § The root CA is called the Root of the PKI. § The X. 509 PKI is scalable: the length of a trust certificate chain is logarithmic in the size of the graph.

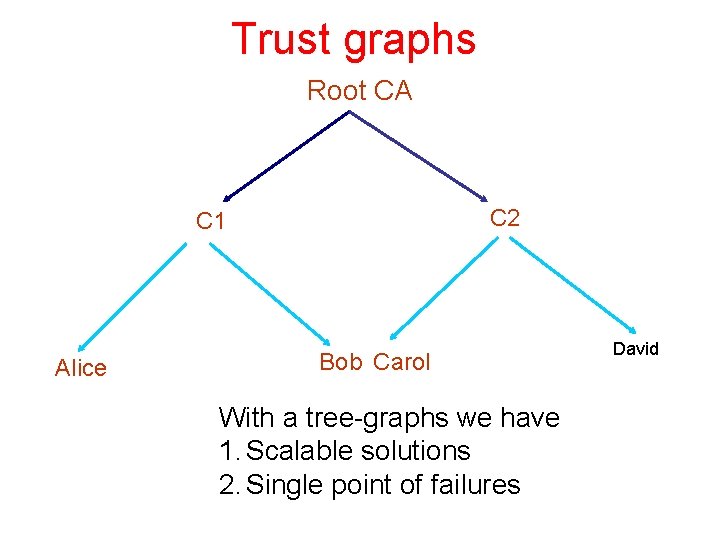
Trust graphs Root CA C 2 C 1 Alice Bob Carol With a tree-graphs we have 1. Scalable solutions 2. Single point of failures David

PKIs § Forest – cross-certifying Root CAs § Other graph solutions § PGPs § Merkle Authentication Tree

PGP certificate chains Provides privacy for electronic mail. The public key of an entity B is certified by “friends” who know him, say E, F, G. PGP certificate for A: E, F, G <<B>>PGP Suppose we have the following chain: A, J <<J>>PGP || K, J, E <<E>>PGP || E, H <<H>>PGP || I, H, G <<G>>PGP || E, F, G, B <<B>>PGP ||

Merkle Authentication Tree Time stamping § Certificates can be kept as data in files, § This reduces the problem of forging certificates to the problem of data integrity.

Merkle Authentication Tree Let Yi be an identifier and its associated public key. f : D D D a function that maps pairs of bit strings to a bit string, where D is the set of bit strings. h: N N D be a cryptographic hash function, where N is the set of natural numbers. h(i, j) = f (h (i, i+j /2 ) , h ( i+j /2 +1 , j) if i < j f (Yi , Yij) otherwise.

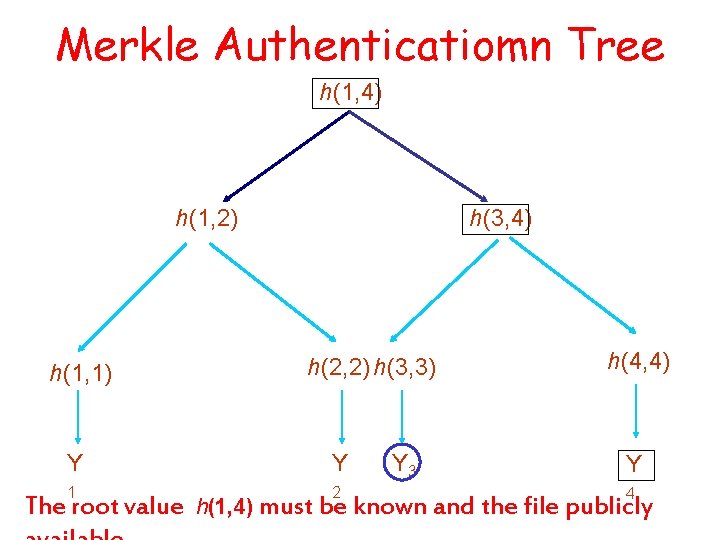
Merkle Authenticatiomn Tree h(1, 4) h(1, 2) h(1, 1) h(3, 4) h(2, 2) h(3, 3) Y Y 1 2 The root value Y 3 h(4, 4) Y 4 h(1, 4) must be known and the file publicly

Merkle Authenticatiomn Tree Suppose that Y 1, Y 2 , …, Yn are in a file, and that user 3 wants to validate Y 3. Compute: • • • h(3, 3) = f (Y 3, Y 3), h(3, 4) = f (h(3, 3), h(4, 4)), (assume that h(4, 4) is available) h(1, 4) = f (h(1, 2), h(3, 4)). (assume that h(1, 2) is available) If h(1, 4) is stored in a public file then. Y 3 can be validated

Merkle Authentication Tree The hashes needed to validate a certificate for Yi are called the authentication path of that certificate. The authentication path for Y 3 is: C 3 = {Y 3, h(4, 4), h(1, 2))}.