Computer Sciences for Engineers September 17 2020 Approximation

Computer Sciences for Engineers September 17, 2020 Approximation of solving nonlinear equations: the interval halving method dr. Nagy Noémi

Approximation of the solution of nonlinear equations

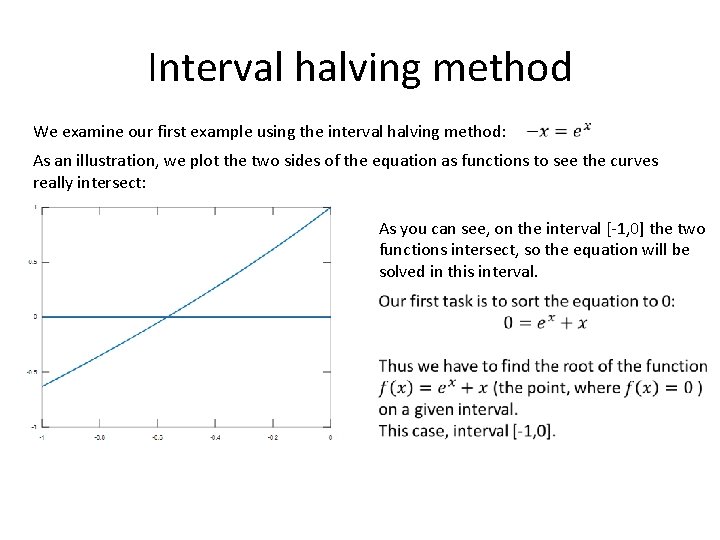
Interval halving method We examine our first example using the interval halving method: As an illustration, we plot the two sides of the equation as functions to see the curves really intersect: As you can see, on the interval [-1, 0] the two functions intersect, so the equation will be solved in this interval.

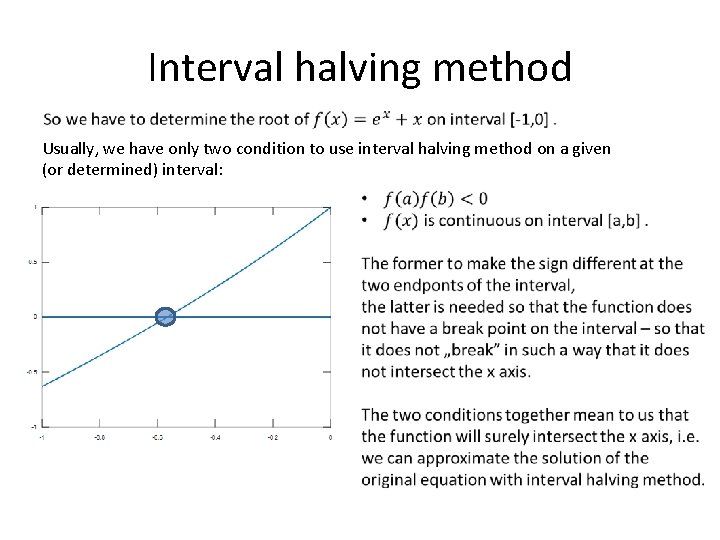
Interval halving method Usually, we have only two condition to use interval halving method on a given (or determined) interval:

Interval halving method Our next step is to verify the conditions. To do this, we substitute the lower and upper endpoints of the interval:

Interval halving method If there is a predefined error for which we eant a more accurate approximatin, we can determine how many steps we will need:

Interval halving method So If there in 5 steps, is a predefined the error will errorbefor below which 0. 05 we eant a more accurate approximatin, we can determine how many steps we will need:

Interval halving method So in 5 steps, the error will be below 0. 05 The simlest to summarize the interval halving method is using tabular form: + n ak bk xk=(ak-bk)/2 f(xk) ε=(bk-ak)/2 1 -1 0 - 0. 5 0. 1065 > 0 0. 5 2 -1 - 0. 5 - 0. 75 - 0. 2776 < 0 0. 25 3 - 0. 75 - 0. 625 - 0. 0897 < 0 0. 125 4 - 0. 625 - 0. 5625 0. 0073 > 0 0. 0625 5 - 0. 625 - 0. 59375 0. 03125 Above n We is the determine calculate the number the table, the lower the it of error, isvalue steps and worth as upper ofhalf writing the endpoints of function the what length the at ofthe value of midpoint. the current ofinterval. thechange. interval function was originally at the lower Obviously, thethe other endpoint interval not Finally, we need to midpoint decide wheter of the interval. the midpoint will be the lower the upper endpoint ofthe We continue algorithm until the last line isdoes reached: here it isor sufficient to determine and upper endpoints, will not change during the approximations. the interval: The sign as of this the value taken in the midpoint s shows that in the first step we have midpoint. to thesee, midpoint on is the positive column. Aswrite we can the error alredy below 0. 05, and the midpoint is a good approximation of the exact solution.