Computer Sciences for Engineers November 19 2020 Approximation

Computer Sciences for Engineers November 19, 2020 Approximation of the eigenvalue and its eigenvector: the power iteration dr. Nagy Noémi

Power iteration The equation is satisfy by λ and v. These are the eigenvalues of the matrix A and the corresponding eigenvector. These are quite difficult to determine for large matrices. . However, the approximation of the largest (and smallest) absolute eigenvalue and its associated eigenvector can be solved using the power iteration (and inverse power iteration): Let our matrix be the following, whose predominant eigenvalue (highest absolute value) and its eigenvector are approximated: The eigenvalues of the matrix and the corresponding eigenvectors can also be obtained by the previously studied method: Vectors v 1 and v 3 were normalized – divided by the infinite norm to compare the result obtained.

Power iteration

Power iteration

Power iteration
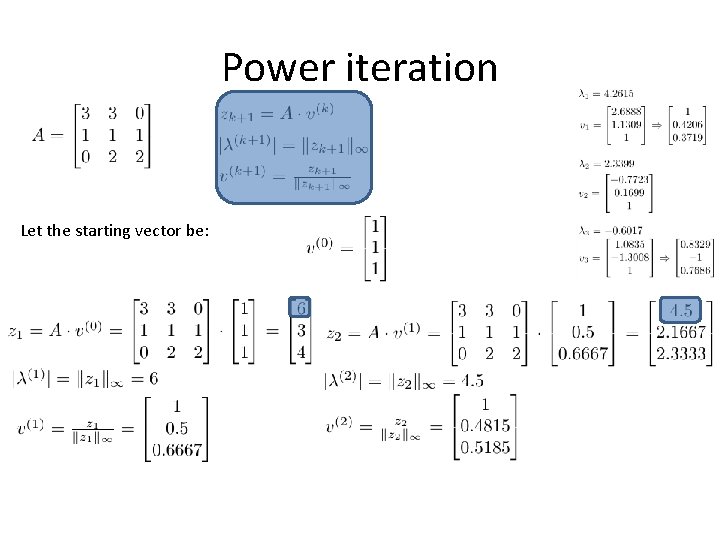
Power iteration Let the starting vector be:
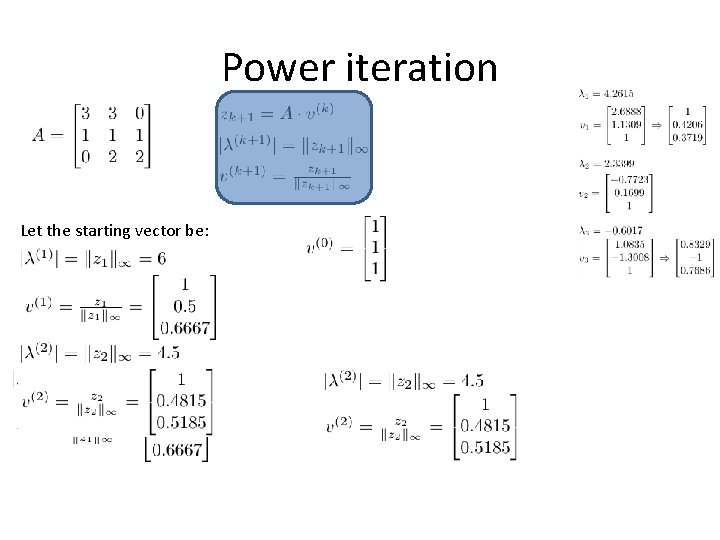
Power iteration Let the starting vector be:
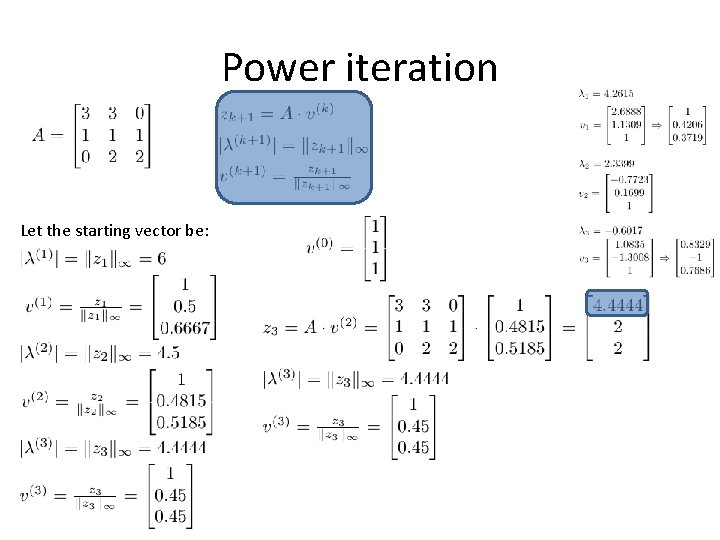
Power iteration Let the starting vector be:
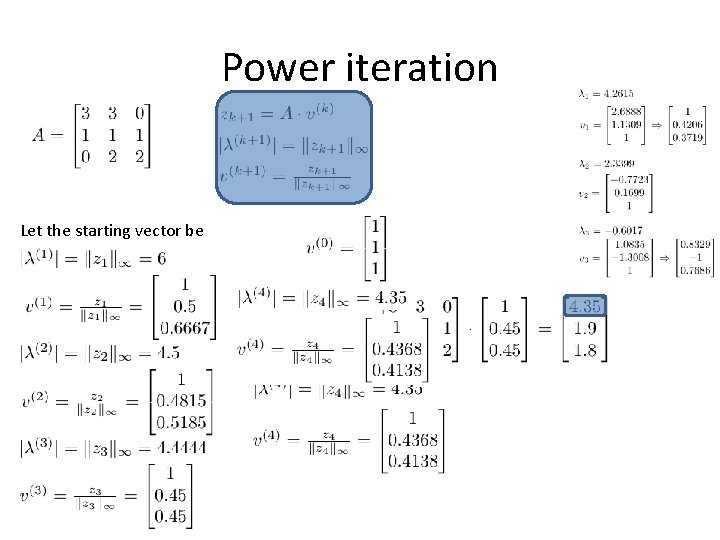
Power iteration Let the starting vector be
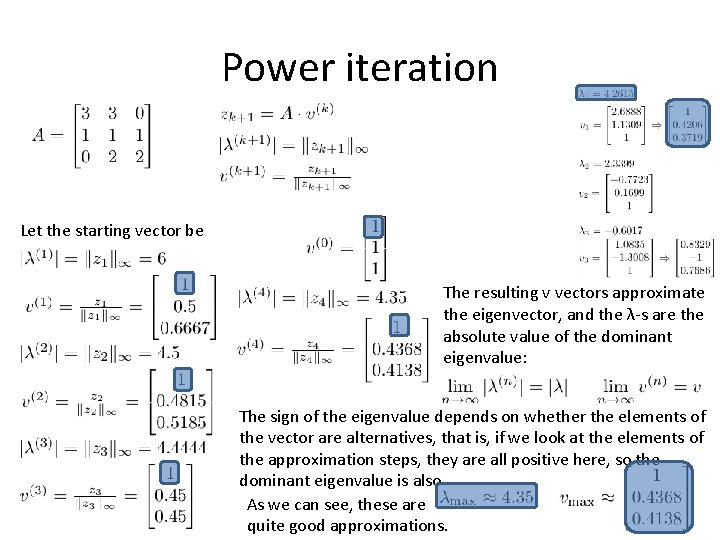
Power iteration Let the starting vector be The resulting v vectors approximate the eigenvector, and the λ-s are the absolute value of the dominant eigenvalue: The sign of the eigenvalue depends on whether the elements of the vector are alternatives, that is, if we look at the elements of the approximation steps, they are all positive here, so the dominant eigenvalue is also As we can see, these are quite good approximations.

The error of the iteration The error of the method can be calculated in several ways: It is the best to use the last two approximations: We can think of the error of the approximation as the difference of the last two λ approximations or as the norm of the difference of the last two approximation vectors.
- Slides: 11