Computer Science 3 03 ASearching Sean P Strout

Computer Science 3 03 A-Searching Sean P. Strout (sps@cs. rit. edu) 2/26/2021 CS 3 - 03 A - Searching (v 1. 01) 1

Sequential Search • A sequential search runs in linear time 0 1 10 7 2 9 3 4 5 6 7 8 9 10 11 4 12 2 5 8 1 6 3 11 • Best Case: search for 10 – O(1) • Average Case: search for 2 – O(6) = O(n/2) • Worst Case: search for 11, 99 – O(12) = O(n) • If collection size doubles, the search time doubles 2/26/2021 CS 3 - 03 A - Searching (v 1. 01) 2

Sequential Search • What happens to the search times if the data is now ordered? – For elements in the array, i. e. 59 – For elements not in the array, i. e. : 0, 31, 99 2/26/2021 0 1 2 3 4 5 6 7 8 9 10 11 5 10 12 15 22 26 32 36 40 44 59 64 CS 3 - 03 A - Searching (v 1. 01) 3

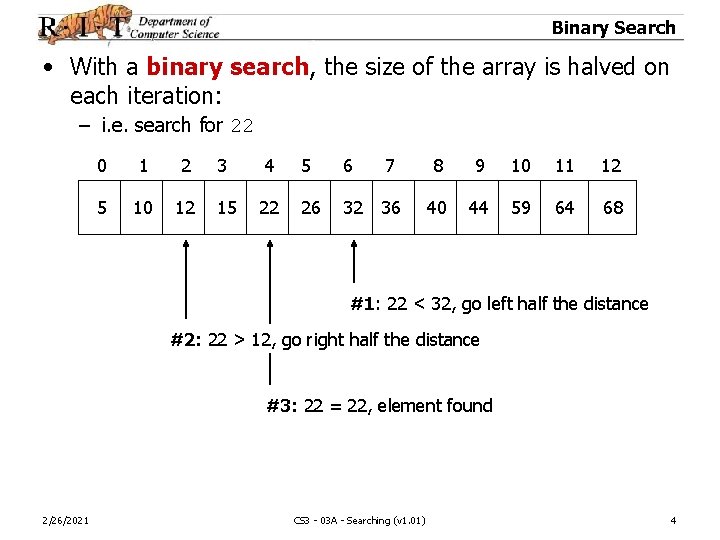
Binary Search • With a binary search, the size of the array is halved on each iteration: – i. e. search for 22 0 1 2 3 4 5 6 7 8 9 10 11 12 5 10 12 15 22 26 32 36 40 44 59 64 68 #1: 22 < 32, go left half the distance #2: 22 > 12, go right half the distance #3: 22 = 22, element found 2/26/2021 CS 3 - 03 A - Searching (v 1. 01) 4

Binary Search • What happens when an element is not found? – i. e. search for 11 0 1 2 3 4 5 6 7 8 9 10 11 12 5 10 12 15 22 26 32 36 40 44 59 64 68 #1: 11 < 32, go left half the distance #2: 11 < 12, go left half the distance #3: 11 > 5, go right half the distance #4: 11 > 10 can’t go right half the distance, element not found 2/26/2021 CS 3 - 03 A - Searching (v 1. 01) 5

Binary Search • The search algorithm uses three indexes to mark the start, middle and end positions – i. e. search for 22 0 1 2 3 4 5 6 7 8 9 10 11 12 5 10 12 15 22 26 32 36 40 44 59 64 68 start middle end • If the middle element is greater than the target, the end moves to middle - 1 and new middle = (start + end)/2 0 1 2 3 4 5 6 7 8 9 10 11 12 5 10 12 15 22 26 32 36 40 44 59 64 68 start 2/26/2021 middle end CS 3 - 03 A - Searching (v 1. 01) 6

Binary Search • If the middle element is greater than the value, the start moves to middle + 1 and new middle = (start + end)/2 0 1 2 3 4 5 6 7 8 9 10 11 12 5 10 12 15 22 26 32 36 40 44 59 64 68 start middle end • If the middle element equals the value, the search stops and the element is found 2/26/2021 CS 3 - 03 A - Searching (v 1. 01) 7

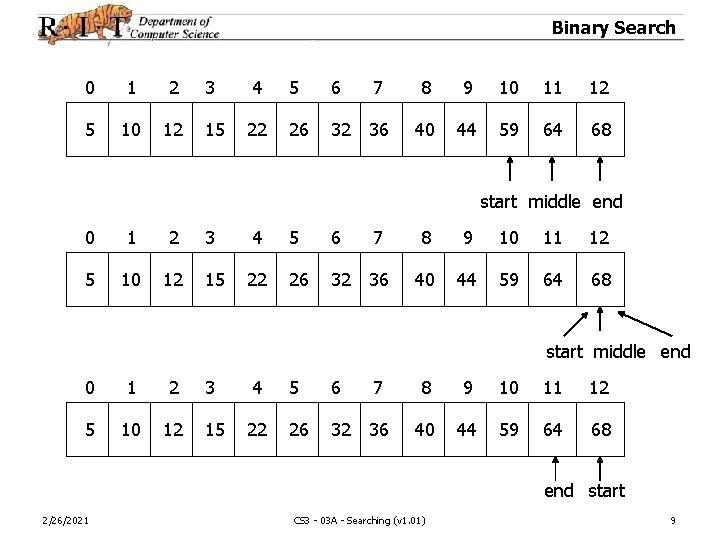
Binary Search • If the element is not in the collection, the start index will eventually exceed the end index – i. e. search for 65 0 1 2 3 4 5 6 7 8 9 10 11 12 5 10 12 15 22 26 32 36 40 44 59 64 68 start middle end 0 1 2 3 4 5 6 7 8 9 10 11 12 5 10 12 15 22 26 32 36 40 44 59 64 68 start 2/26/2021 CS 3 - 03 A - Searching (v 1. 01) middle end 8

Binary Search 0 1 2 3 4 5 6 7 8 9 10 11 12 5 10 12 15 22 26 32 36 40 44 59 64 68 start middle end 0 1 2 3 4 5 6 7 8 9 10 11 12 5 10 12 15 22 26 32 36 40 44 59 64 68 end start 2/26/2021 CS 3 - 03 A - Searching (v 1. 01) 9

Binary Search • Given the follow collection using a binary search: 0 1 2 3 4 5 6 7 8 9 10 11 12 5 10 12 15 22 26 32 36 40 44 59 64 68 • How many accesses will it take to locate element: – – 2/26/2021 32 44 5 99 CS 3 - 03 A - Searching (v 1. 01) 10

Binary Search • A binary search happens in logarithmic time – Best Case: O(1) – Average Case: O(log 2 n) – Worst Case: O(log 2 n) • x=log 2 n, where x is the power we raise 2 to, to get n – – log 21 log 22 log 24 log 28 = = 0 1 2 3 (20 (21 (22 (23 = = 1) 2) 4) 8) • O(log 2 n) grows slower than O(n) but the collection must be sorted first 2/26/2021 CS 3 - 03 A - Searching (v 1. 01) 11

Binary Search - Testing Your Understanding • Write a sample program, Test. Search. java, which demonstrates a binary search of your Instrumented. Array from lab 2 • The main method should: – Read in a single argument which is the Integer to search for – Create an Instrumented. Array with the following Integer values: 1 -128 – Call the search method: // Returns the position of the target in the // array, or -1 if is not present public static int binary. Search(Instrumented. Array array, int target); 2/26/2021 CS 3 - 03 A - Searching (v 1. 01) 12

Binary Search - Testing Your Understanding • main method continued: – Print out the results of the search. Position = -1 if not found. Array accessed # times. Value i at position #. • Verify the algorithm is O(log 2128)= 7 – Search for 0, 1, 63, 64, 65 and 128 – Search for elements not in the collection – What elements give an access time of 3? • I have a perl script which will run all the tests and print results/statistics. Copy it to your local directory to run: cp /usr/local/pub/sps/courses/cs 3/search/Binary. Search/run. pl. 2/26/2021 CS 3 - 03 A - Searching (v 1. 01) 13

Indexed Binary Search • Consider the binary search time when N=1000 0 1 1 2 2 3 . . . 998 999 . . . 999 1000 • O(log 2 N) = O(log 21000) = ~9. 97 accesses • The search time on a large data set can be improved by building an index table for looking up the subset range for the target value 2/26/2021 CS 3 - 03 A - Searching (v 1. 01) 14

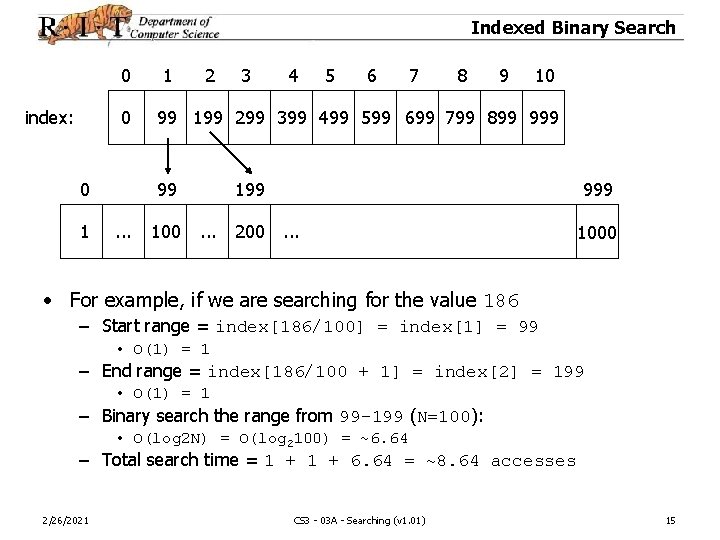
Indexed Binary Search 0 index: 0 0 1 1 2 4 5 6 7 8 9 10 99 199 299 399 499 599 699 799 899 99. . . 3 100 199. . . 200 999. . . 1000 • For example, if we are searching for the value 186 – Start range = index[186/100] = index[1] = 99 • O(1) = 1 – End range = index[186/100 + 1] = index[2] = 199 • O(1) = 1 – Binary search the range from 99 -199 (N=100): • O(log 2 N) = O(log 2100) = ~6. 64 – Total search time = 1 + 6. 64 = ~8. 64 accesses 2/26/2021 CS 3 - 03 A - Searching (v 1. 01) 15

Indexed Binary Search • Given the following indexed collection using a binary search: 0 index: 0 0 1 1 2 4 5 6 7 8 9 10 99 199 299 399 499 599 699 799 899 99. . . 3 100 199. . . 200 299. . . 300 999. . . 1000 • How many accesses will it take to find the element: – – – 2/26/2021 250 275 262 256 251 CS 3 - 03 A - Searching (v 1. 01) 16

Ternary Search • A ternary search builds on the idea of binary search by splitting the search space into thirds (vs. halves) third = (end - start) / 3 0 1 2 3 4 5 6 7 8 9 10 11 12 5 10 12 15 22 26 32 36 40 44 59 64 68 start probe = start + third end • For each iteration, compute third & probe and compare element at the probe: – If target is less than, move end to probe - 1 – If target is greater than, move start to probe + 1 and recompute probe as end - third. Compare the element at probe: • If less than, end = probe - 1 • If greater than, start = probe + 1 2/26/2021 CS 3 - 03 A - Searching (v 1. 01) 17

Ternary Search • Trace through a search for 44 and 12 : 0 1 2 3 4 5 6 7 8 9 10 11 12 5 10 12 15 22 26 32 36 40 44 59 64 68 • The ternary search time is O(log 3 N) 2/26/2021 CS 3 - 03 A - Searching (v 1. 01) 18

ACME Project • For part 1, an echo server for simulating the bank is being provided for you: – /usr/local/pub/sps/courses/cs 3/projects/ACME/Echo. Bank. java • To run you must specify an unused port: % java Echo. Bank 9125 Echo. Bank listening on port 9125 • When a client successful connects to the echo server: Accepted socket[addr=/#. #, port=####, localport=9125] • When a client closes the socket to the echo server: ATM has terminated the connection 2/26/2021 CS 3 - 03 A - Searching (v 1. 01) 19

ACME Project • The echo server will continuously read Banking. Message objects from the client: Received message VALIDATE 12345 0 • The echo server will always send back a Banking. Message object to the client indicating the operation was successful: Sent message SUCCESS_RESPONSE 12345 100000 • The echo server can only accept one client connection at a time, and must be terminated manually • Eclipse: Running ATM and Echo. Server and selecting their console output 2/26/2021 CS 3 - 03 A - Searching (v 1. 01) 20

Revision History • Revision History – 2/26/2021 v 1. 00, 3/14/05 12: 38 PM, sps Initial revision. CS 3 - 03 A - Searching (v 1. 01) 21