Computer Science 112 Fundamentals of Programming II Searching

Computer Science 112 Fundamentals of Programming II Searching, Sorting, and Complexity Analysis

Things to Desire in a Program • Correctness • Robustness • Maintainability • Efficiency

Measuring Efficiency • Empirical - use clock to get actual running times for different inputs • Problems: – Different machines have different running times – Some running times are so long that it is impractical to check them

Measuring Efficiency • Analytical - use pencil and paper to determine the abstract amount of work that a program does for different inputs • Advantages: – Machine independent – Can predict running times of programs that are impractical to run

Complexity Analysis • Pick an instruction that will run most often in the code • Determine the number of times this instruction will be executed as a function of the size of the input data • Focus on abstract units of work, not actual running time

Example: Search for the Minimum def our. Min(lyst): min. So. Far = lyst[0] for item in lyst: min. So. Far = min(min. So. Far, item) return min. So. Far We focus on the assignment (=) inside the loop and ignore the other instructions. for a list of length 1, one assignment for a list of length 2, 2 assignments. for a list of length n, n assignments

Big-O Notation • Big-O notation expresses the amount of work a program does as a function of the size of the input • O(N) stands for order of magnitude N, or order of N for short • Search for the minimum is O(N), where N is the size of the input (the length of a list, the magnitude of a number, etc. )

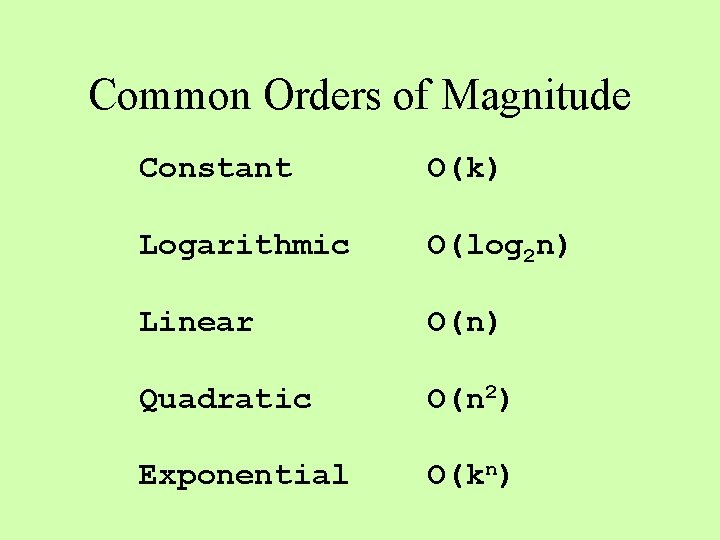
Common Orders of Magnitude Constant O(k) Logarithmic O(log 2 n) Linear O(n) Quadratic O(n 2) Exponential O(kn)

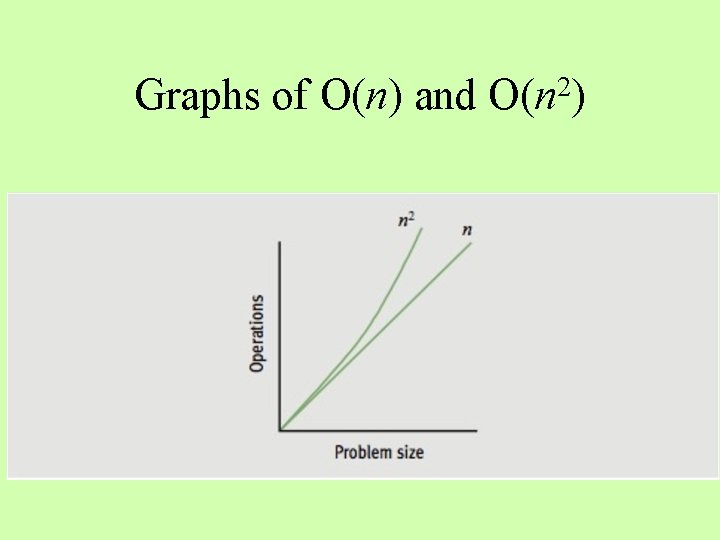
Graphs of O(n) and 2 O(n )

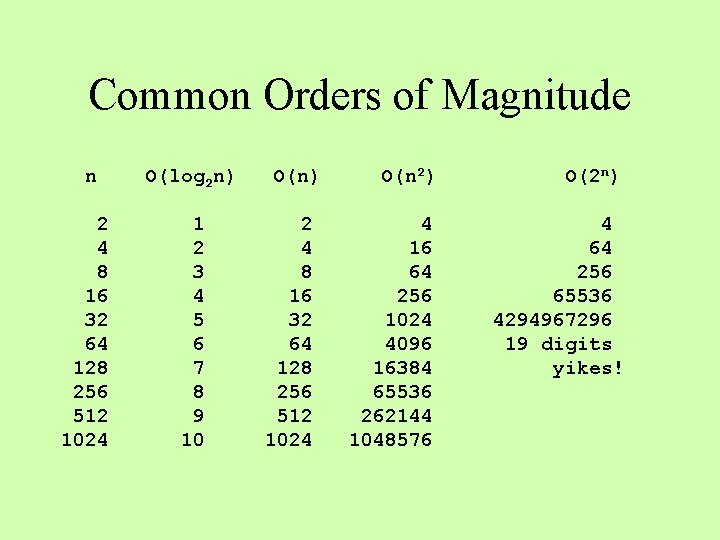
Common Orders of Magnitude n O(log 2 n) 2 4 8 16 32 64 128 256 512 1024 1 2 3 4 5 6 7 8 9 10 O(n) 2 4 8 16 32 64 128 256 512 1024 O(n 2) O(2 n) 4 16 64 256 1024 4096 16384 65536 262144 1048576 4 64 256 65536 4294967296 19 digits yikes!

Approximations • Suppose an algorithm requires exactly 3 N + 3 steps • As N gets very large, the difference between N and N + K becomes negligible (where K is a constant) • As N gets very large, the difference between N and N / K or N * K also becomes negligible • Use the highest degree term in a polynomial and drop the others (N 2 – N)/2 N 2

Example Approximations n 2 4 8 16 32 64 128 256 512 1024 O(n) + 2 O(n 2) 4 4 6 16 10 64 18 256 34 1024 66 4096 130 16384 258 65536 514 262144 1026 1048576 O(n 2) + n 6 20 72 272 1056 5050 16512 65792 262656 1049600

Example: Sequential Search def our. In(target, lyst): for item in lyst: if item == target: return True return False # Found target # Target not there Which instruction do we pick? How fast is its rate of growth as a function of n? Is there a worst case and a best case? An average case?

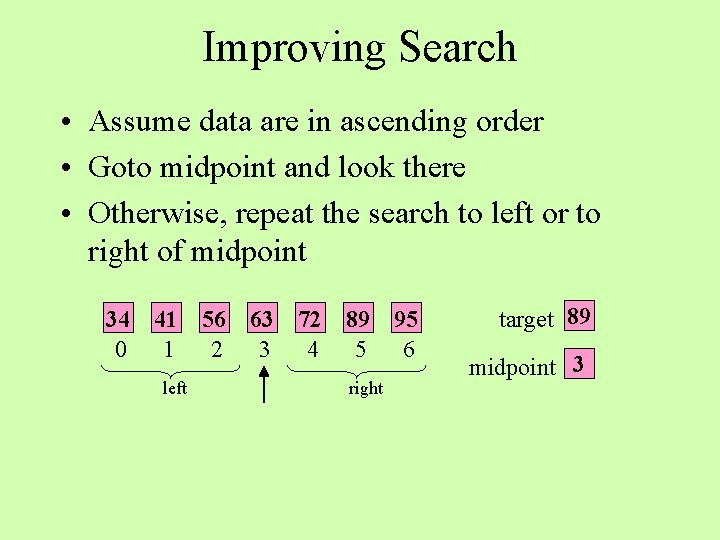
Improving Search • Assume data are in ascending order • Goto midpoint and look there • Otherwise, repeat the search to left or to right of midpoint 34 0 41 1 left 56 2 63 3 72 4 89 5 right 95 6 target 89 midpoint 3

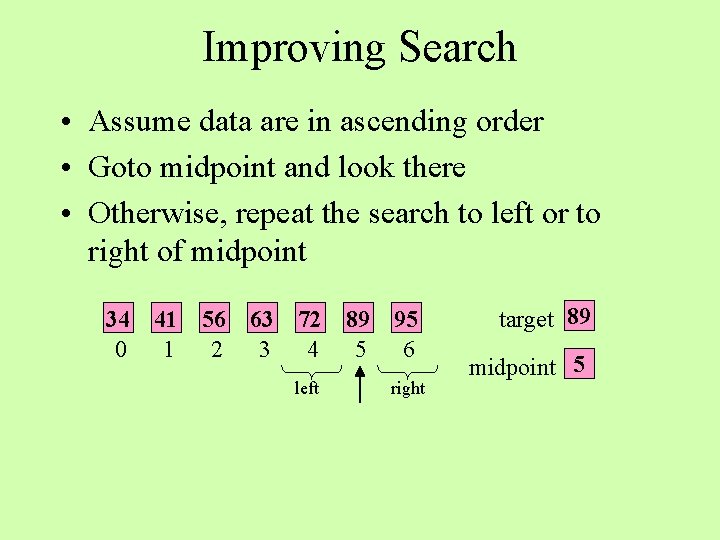
Improving Search • Assume data are in ascending order • Goto midpoint and look there • Otherwise, repeat the search to left or to right of midpoint 34 0 41 1 56 2 63 3 72 4 left 89 5 95 6 right target 89 midpoint 5

Example: Binary Search def fast. Our. In(target, sorted. Lyst): left = 0 right = len(sorted. Lyst) - 1 while left <= right: midpoint = (left + right) // 2 if target == sorted. Lyst[midpoint]: return True elif target < sorted. Lyst[midpoint]: right = midpoint - 1 else: left = midpoint + 1 return False

Analysis while left <= right: midpoint = (left + right) // 2 if target == sorted. Lyst[midpoint]: return True elif target < sorted. Lyst[midpoint]: right = midpoint - 1 else: left = midpoint + 1 How many times will == be executed in the worst case?

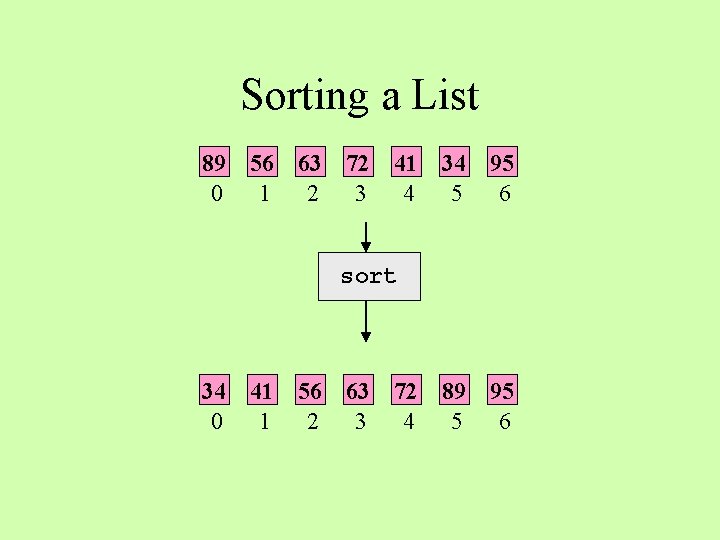
Sorting a List 89 0 56 1 63 2 72 3 41 4 34 5 95 6 89 5 95 6 sort 34 0 41 1 56 2 63 3 72 4

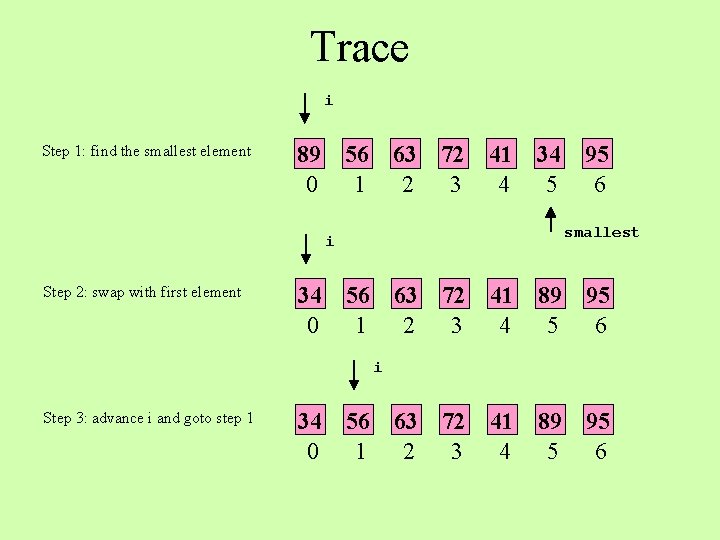
Selection Sort • For each position i in the list – Select the smallest element from i to n - 1 – Swap it with the ith one

Trace i Step 1: find the smallest element 89 0 56 1 63 2 72 3 41 4 34 5 smallest i Step 2: swap with first element 34 0 95 6 56 1 63 2 72 3 41 89 4 5 95 6 i Step 3: advance i and goto step 1 34 0 56 1

Design of Selection Sort for each i from 0 to n - 1 min. Index = min. In. Range(lyst, i, n) if min. Index != i swap(lyst, i, min. Index) • min. In. Range returns the index of the smallest element • swap exchanges the elements at the specified positions

Implementation def selection. Sort(lyst): n = len(lyst) for i in range(n): min. Index = min. In. Range(lyst, i, n) if min. Index != i: swap(lyst, i, min. Index)

Implementation def selection. Sort(lyst): n = len(lyst) for i in range(n): min. Index = min. In. Range(lyst, i, n) if min. Index != i: swap(lyst, i, min. Index) def min. In. Range(lyst, i, n): min. Value = lyst[i] min. Index = i for j in range(i, n): if lyst[j] < min. Value: min. Value = lyst[j] min. Index = j return min. Index

Implementation def selection. Sort(lyst): n = len(lyst) for i in range(n): min. Index = min. In. Range(lyst, i, n) if min. Index != i: swap(lyst, i, min. Index) def min. In. Range(lyst, i, n): min. Value = lyst[i] min. Index = i for j in range(i, n): if lyst[j] < min. Value: min. Value = lyst[j] min. Index = j return min. Index def swap(lyst, i, j): lyst[i], lyst[j] = lyst[j], lyst[i]

Analysis of Selection Sort • The main loop runs approximately n times • Thus, the function min. In. Range runs n times • Within the function min. In. Range, a loop runs n - i times

Analysis of Selection Sort Overall, the number of comparisons performed in function min. In. Range is n - 1 + n - 2 + n - 3 +. . + 1 = (n 2 – n) / 2 n 2

The Fibonacci Series 1 1 2 3 5 8 13. . . fib(n) = 1, when n = 1 or n = 2 fib(n) = fib(n – 1) + fib(n – 2) otherwise def fib(n): if n == 1 or n == 2: return 1 else: return fib(n – 1) + fib(n – 2)

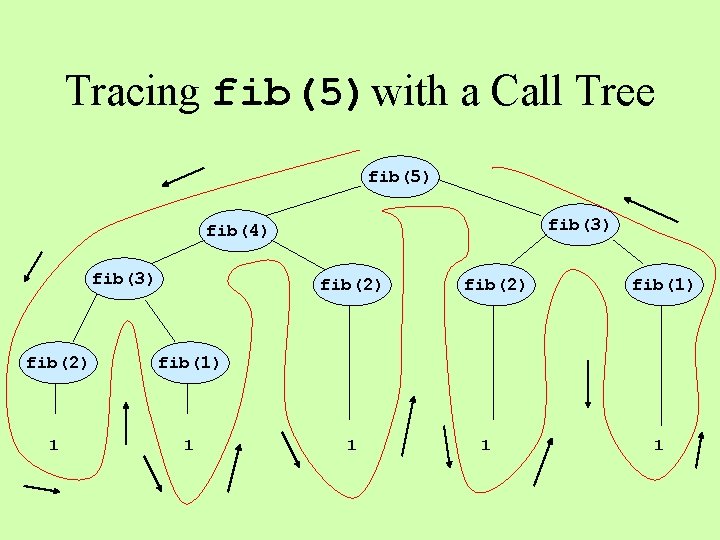
Tracing fib(5)with a Call Tree fib(5) fib(3) fib(4) fib(3) fib(2) fib(1) 1 1 1 fib(2) 1 fib(1) 1

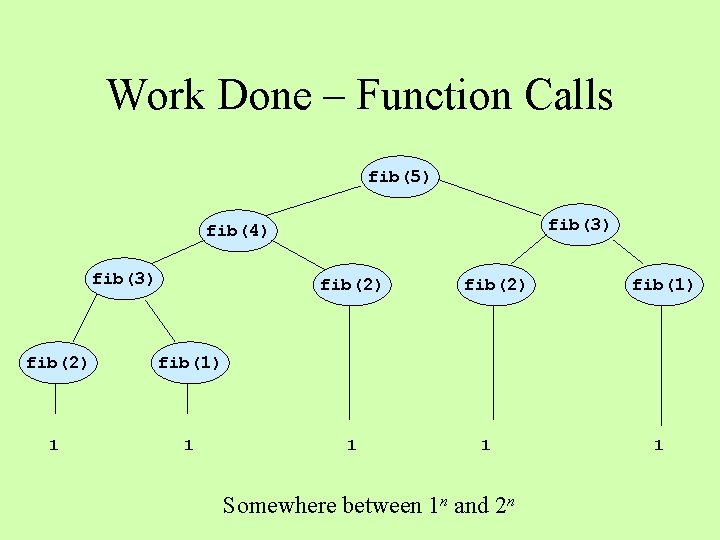
Work Done – Function Calls fib(5) fib(3) fib(4) fib(3) fib(2) fib(1) 1 1 1 fib(2) 1 Somewhere between 1 n and 2 n fib(1) 1

For Wednesday Finding Faster Algorithms