Computer Science 112 Fundamentals of Programming II Introduction

Computer Science 112 Fundamentals of Programming II Introduction to Trees

Categories of Collections • Unordered (bags, sets, dictionaries) • Linear (stacks, queues, lists) • Hierarchical (trees) • Graphs

Why Trees? • Organization charts • Decision flow charts • Logarithmic searching • Language processing

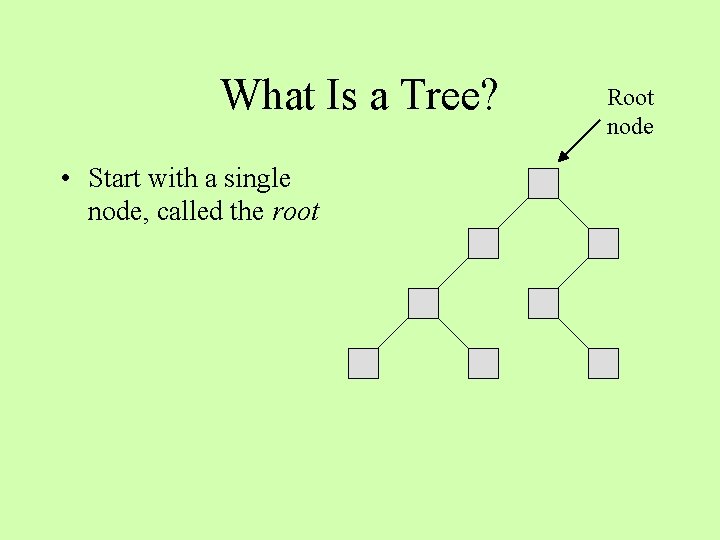
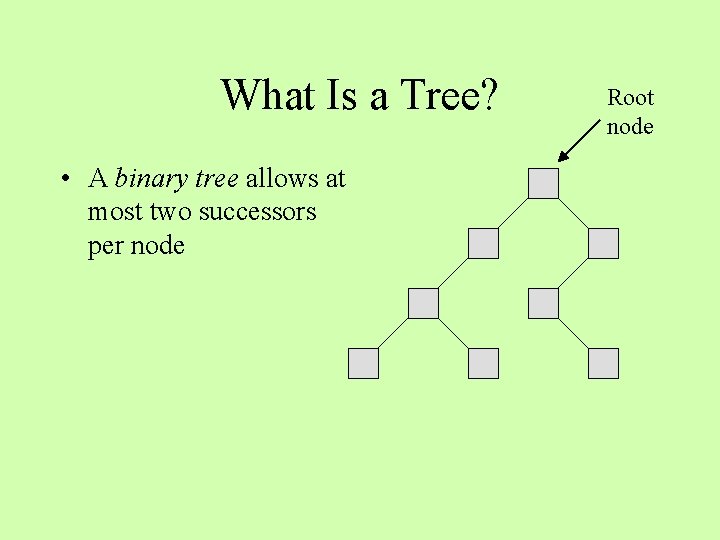
What Is a Tree? • Each item has at most one predecessor • Each item can have many successors

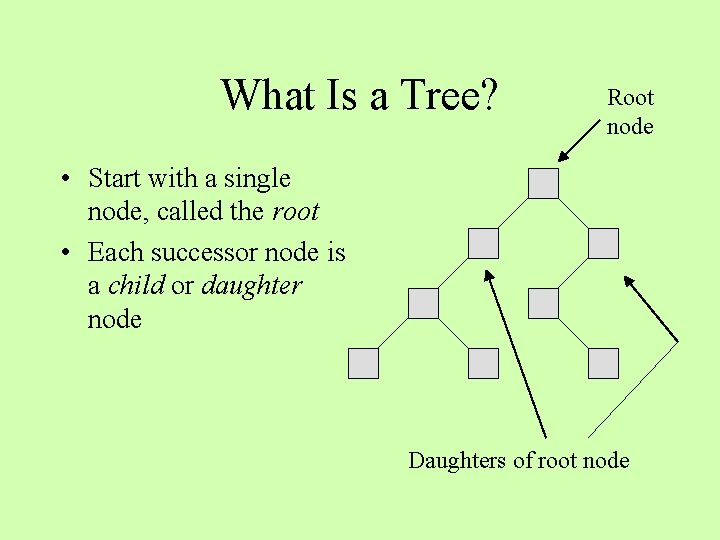
What Is a Tree? • Start with a single node, called the root Root node

What Is a Tree? Root node • Start with a single node, called the root • Each successor node is a child or daughter node Daughters of root node

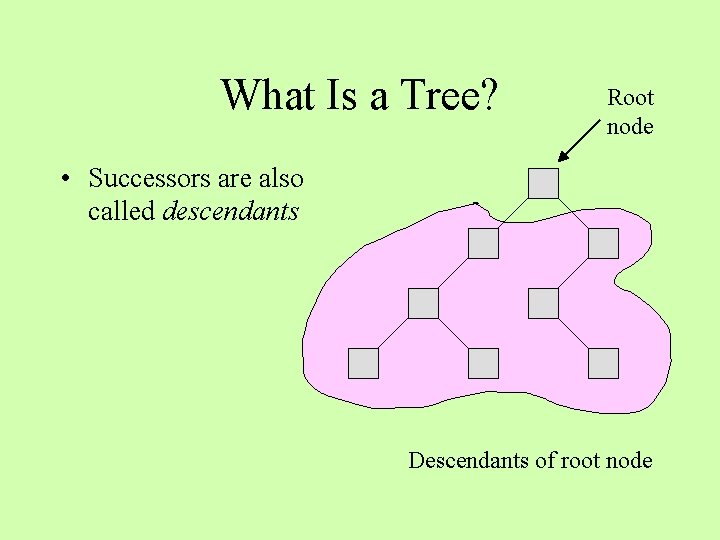
What Is a Tree? Root node • Successors are also called descendants Descendants of root node

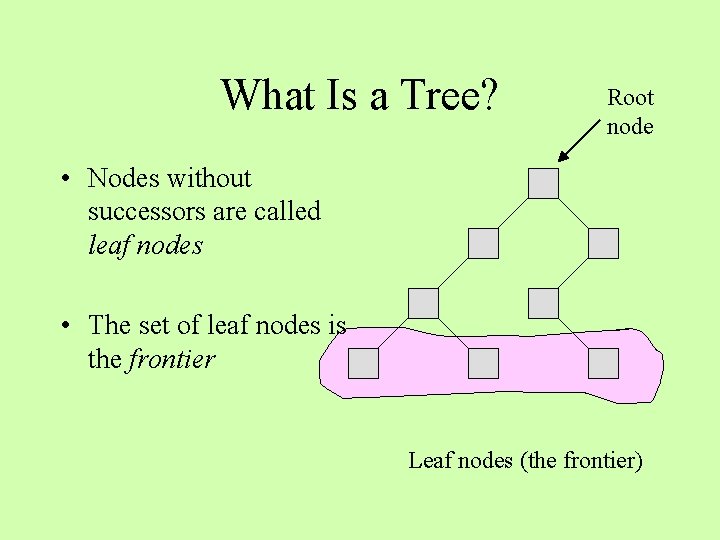
What Is a Tree? Root node • Nodes without successors are called leaf nodes • The set of leaf nodes is the frontier Leaf nodes (the frontier)

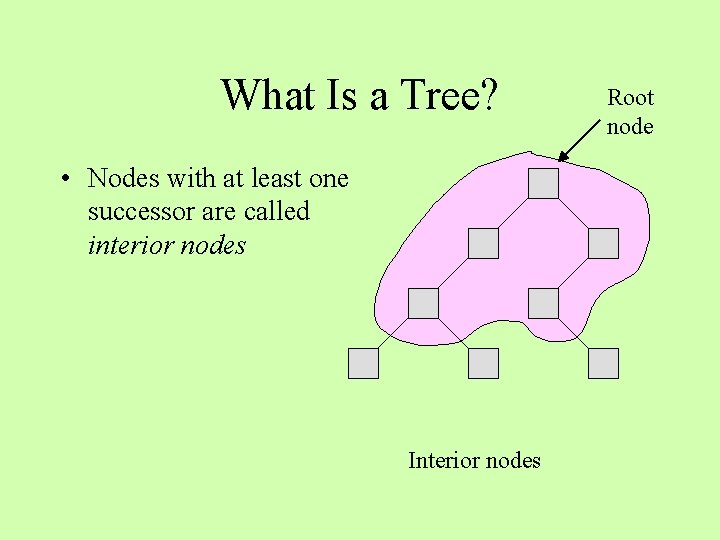
What Is a Tree? • Nodes with at least one successor are called interior nodes Interior nodes Root node

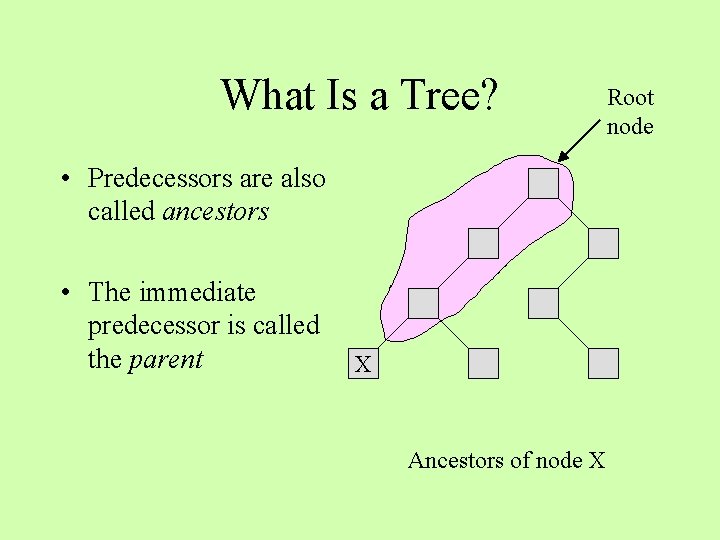
What Is a Tree? • Predecessors are also called ancestors • The immediate predecessor is called the parent X Ancestors of node X Root node

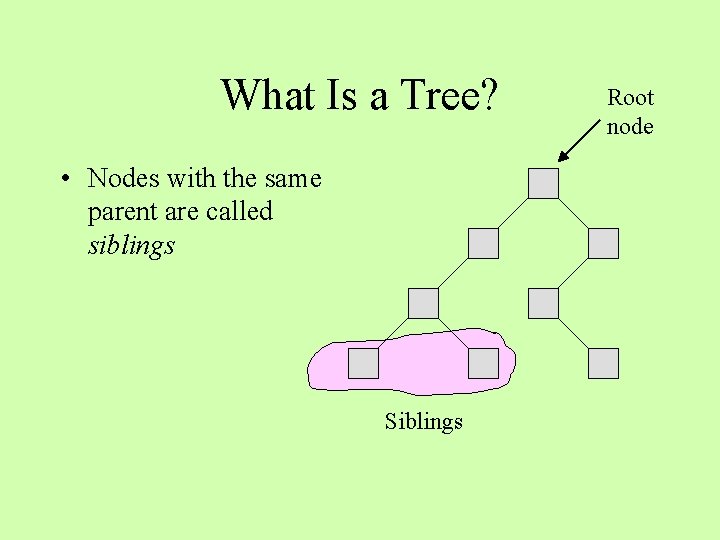
What Is a Tree? • Nodes with the same parent are called siblings Siblings Root node

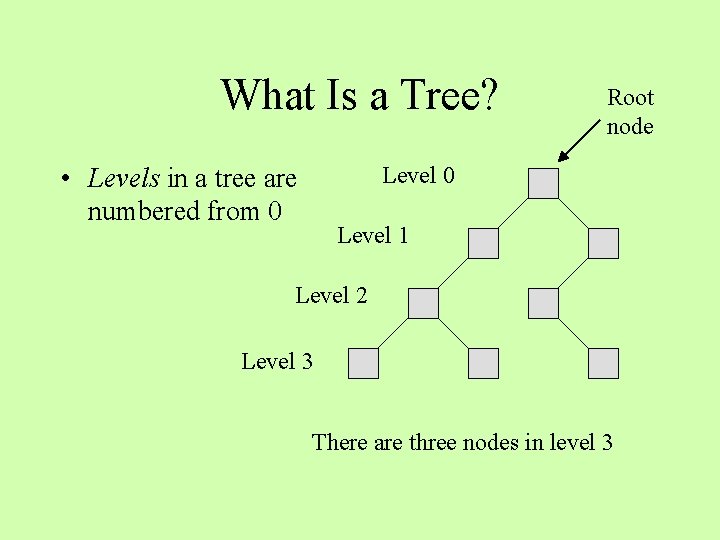
What Is a Tree? • Levels in a tree are numbered from 0 Root node Level 0 Level 1 Level 2 Level 3 There are three nodes in level 3

What Is a Tree? • A binary tree allows at most two successors per node Root node

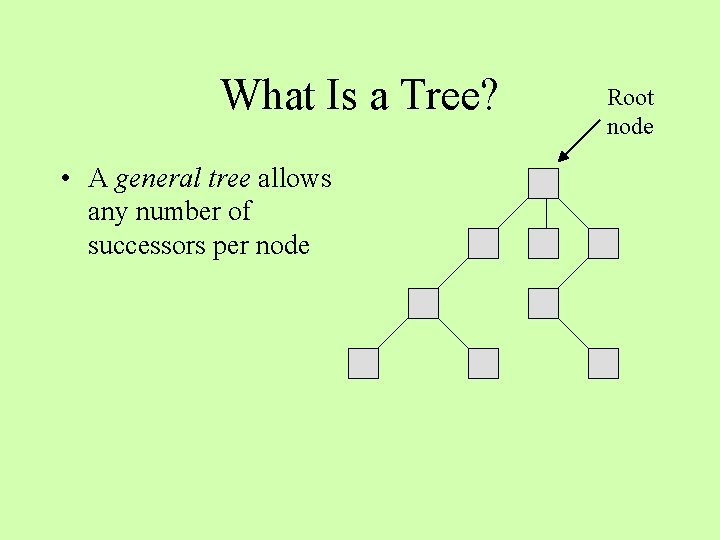
What Is a Tree? • A general tree allows any number of successors per node Root node

Trees as Recursive Data Structures • A tree is either – empty, or – consists of a node containing • a datum • one or more subtrees Each subtree is itself another tree

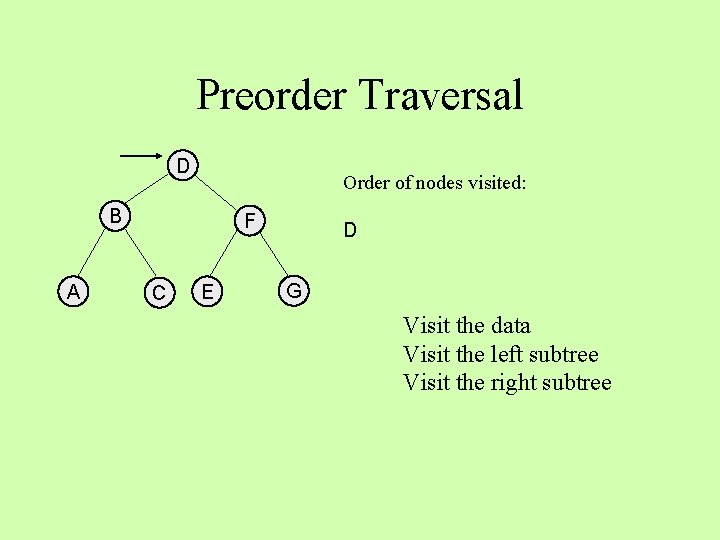
Tree Traversals • We’d like to visit each data item in a tree • Are the items randomly ordered, as in a bag or set? • Think of visiting the data in a node, and its left and right subtrees, in some order

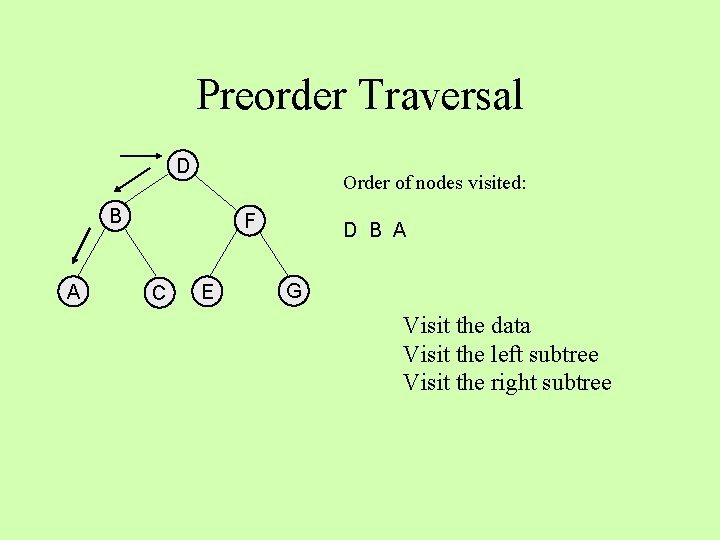
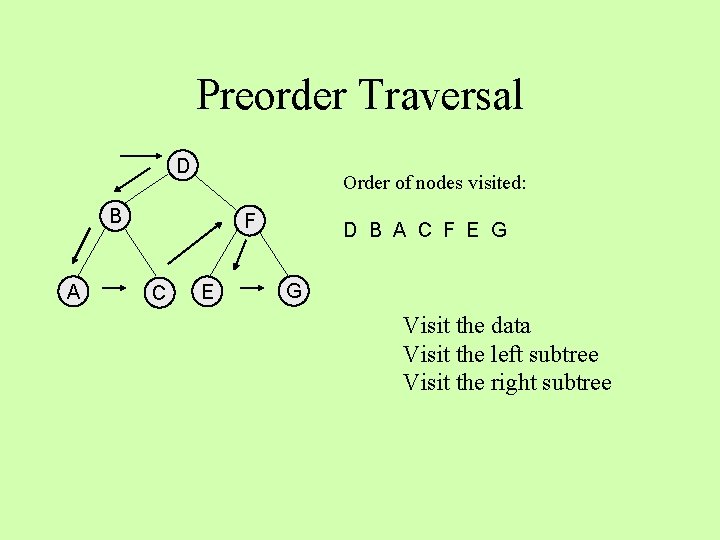
Preorder Traversal D Order of nodes visited: B A F C E D G Visit the data Visit the left subtree Visit the right subtree

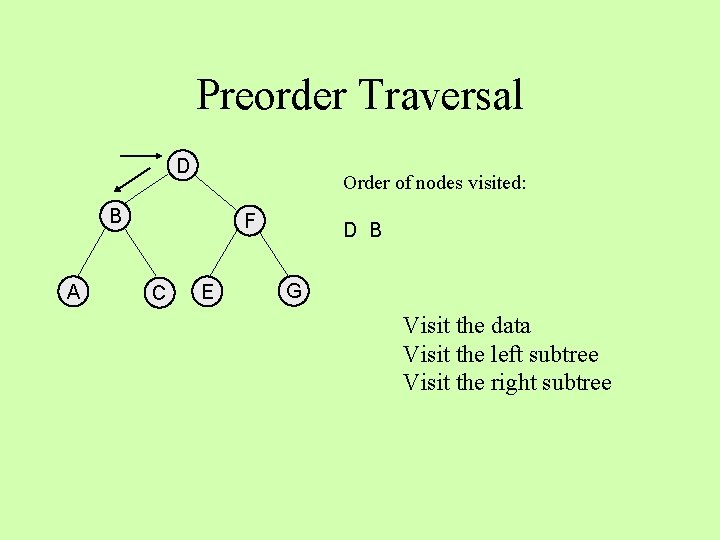
Preorder Traversal D Order of nodes visited: B A F C E D B G Visit the data Visit the left subtree Visit the right subtree

Preorder Traversal D Order of nodes visited: B A F C E D B A G Visit the data Visit the left subtree Visit the right subtree

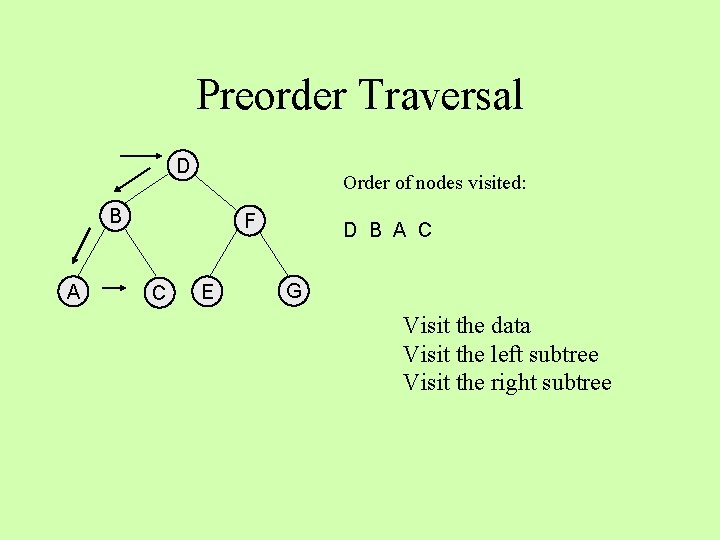
Preorder Traversal D Order of nodes visited: B A F C E D B A C G Visit the data Visit the left subtree Visit the right subtree

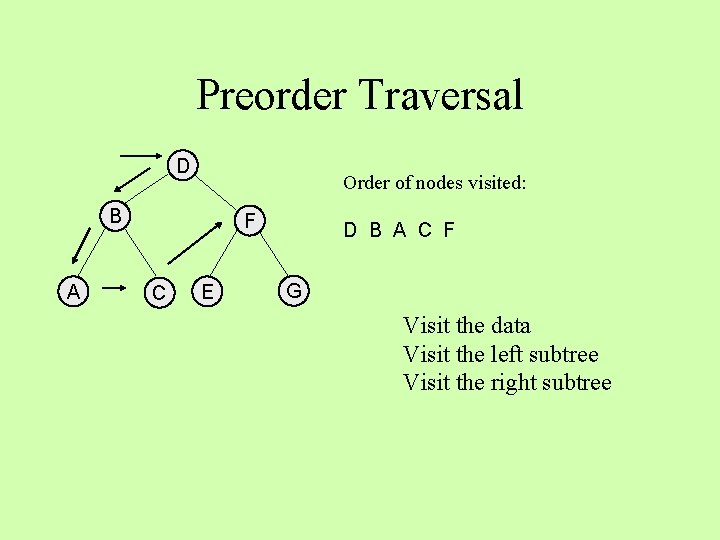
Preorder Traversal D Order of nodes visited: B A F C E D B A C F G Visit the data Visit the left subtree Visit the right subtree

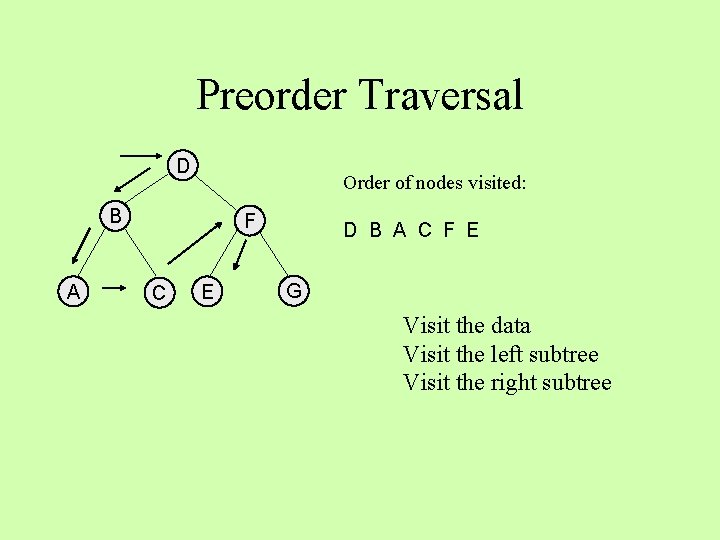
Preorder Traversal D Order of nodes visited: B A F C E D B A C F E G Visit the data Visit the left subtree Visit the right subtree

Preorder Traversal D Order of nodes visited: B A F C E D B A C F E G G Visit the data Visit the left subtree Visit the right subtree

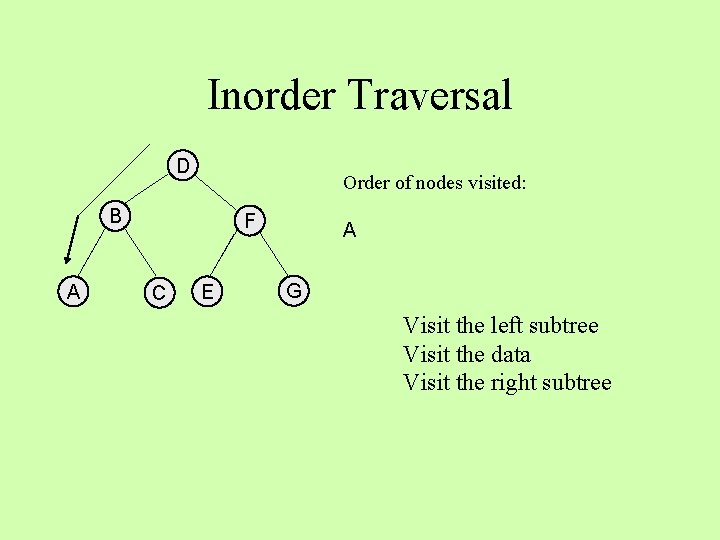
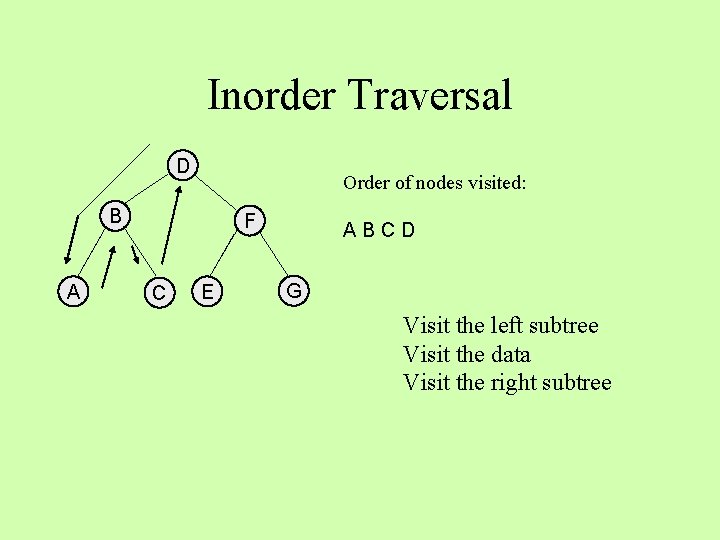
Inorder Traversal D Order of nodes visited: B A F C E A G Visit the left subtree Visit the data Visit the right subtree

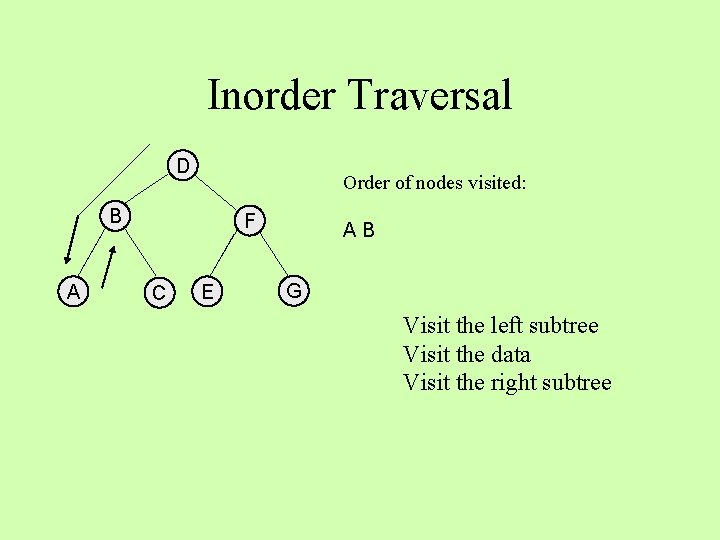
Inorder Traversal D Order of nodes visited: B A F C E AB G Visit the left subtree Visit the data Visit the right subtree

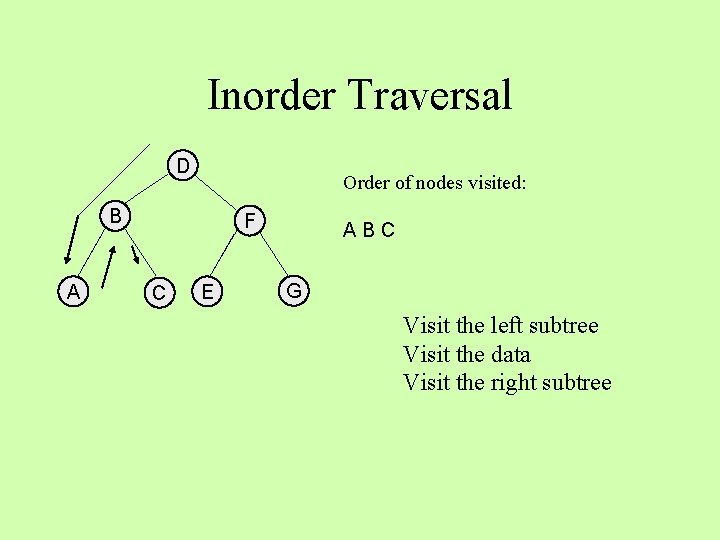
Inorder Traversal D Order of nodes visited: B A F C E ABC G Visit the left subtree Visit the data Visit the right subtree

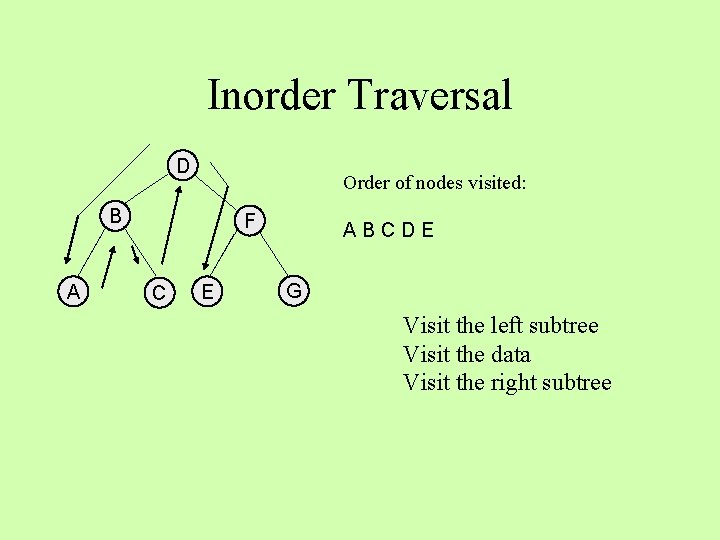
Inorder Traversal D Order of nodes visited: B A F C E ABCD G Visit the left subtree Visit the data Visit the right subtree

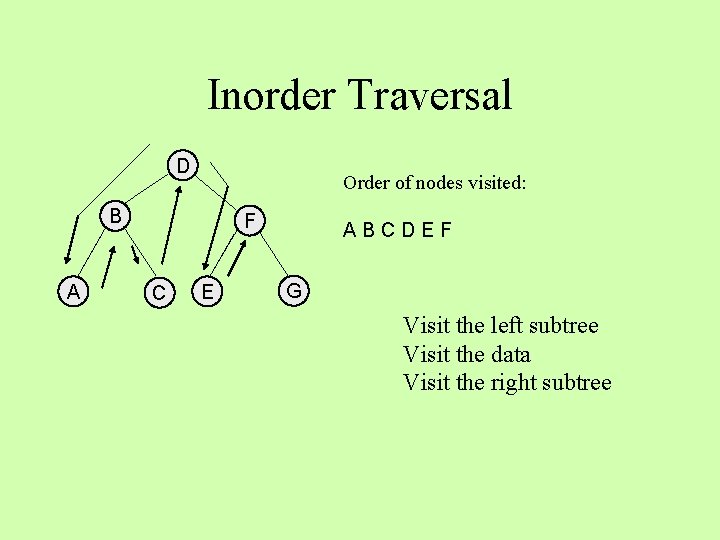
Inorder Traversal D Order of nodes visited: B A F C E ABCDE G Visit the left subtree Visit the data Visit the right subtree

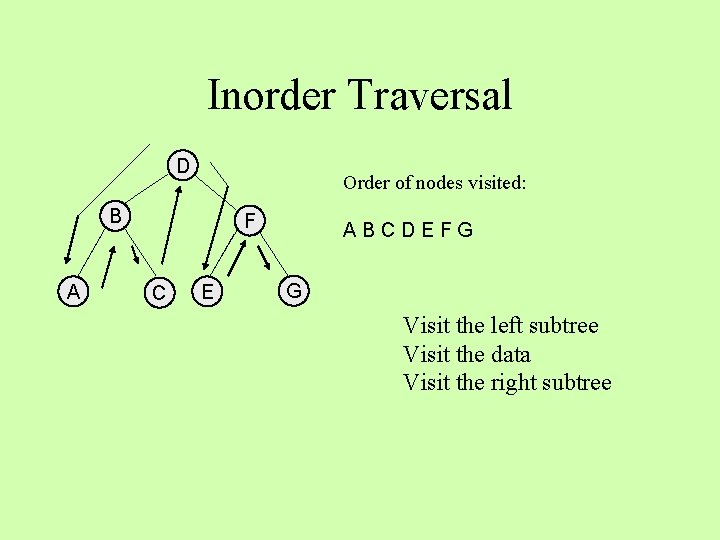
Inorder Traversal D Order of nodes visited: B A F C E ABCDEF G Visit the left subtree Visit the data Visit the right subtree

Inorder Traversal D Order of nodes visited: B A F C E ABCDEFG G Visit the left subtree Visit the data Visit the right subtree

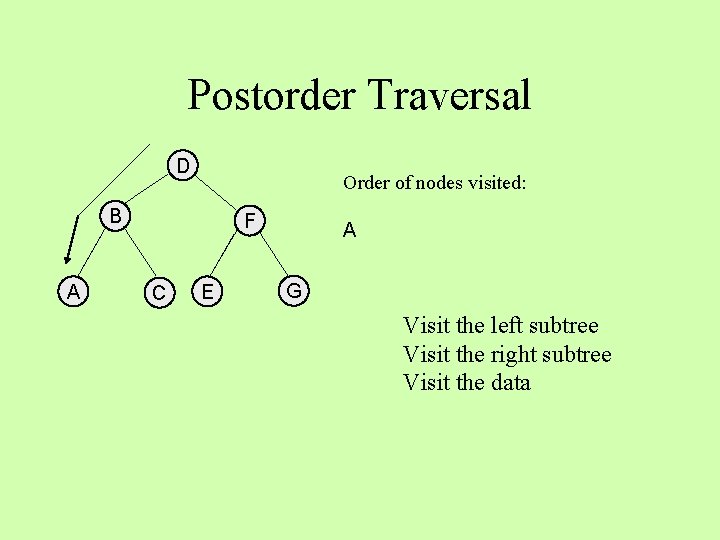
Postorder Traversal D Order of nodes visited: B A F C E A G Visit the left subtree Visit the right subtree Visit the data

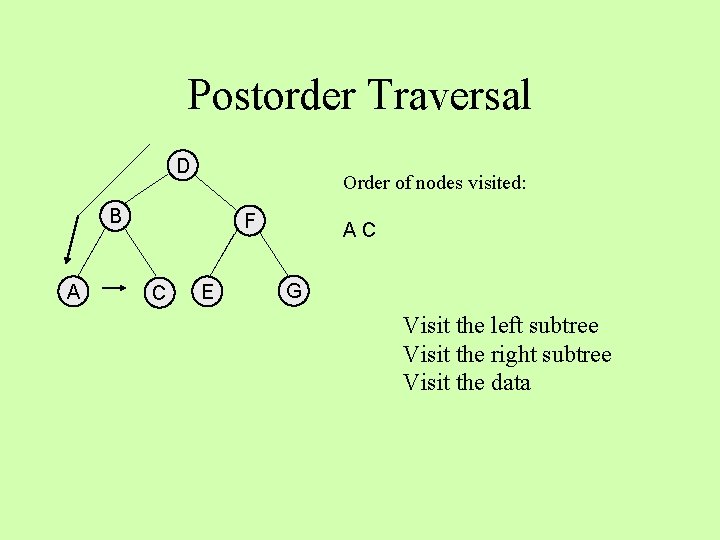
Postorder Traversal D Order of nodes visited: B A F C E AC G Visit the left subtree Visit the right subtree Visit the data

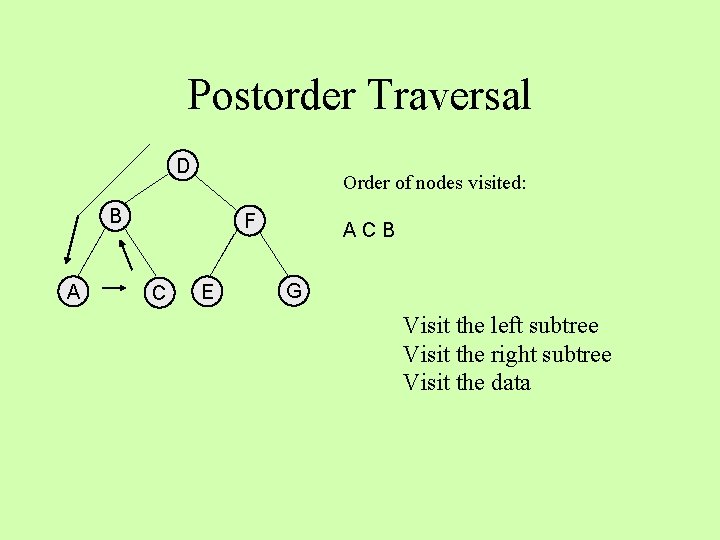
Postorder Traversal D Order of nodes visited: B A F C E ACB G Visit the left subtree Visit the right subtree Visit the data

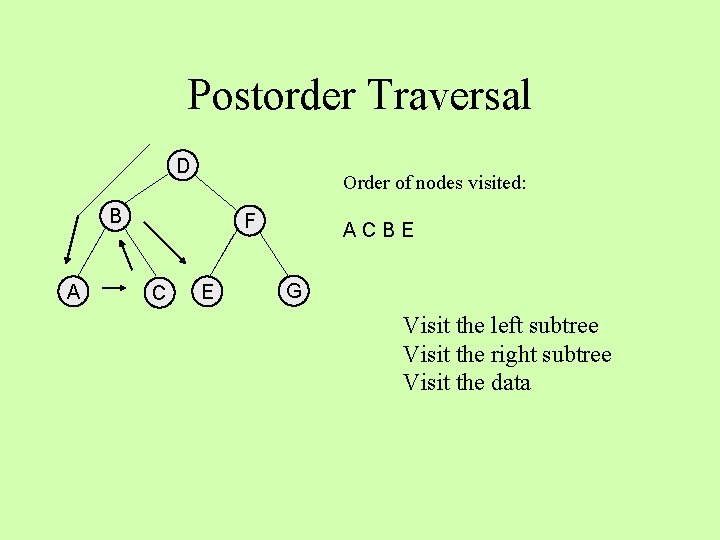
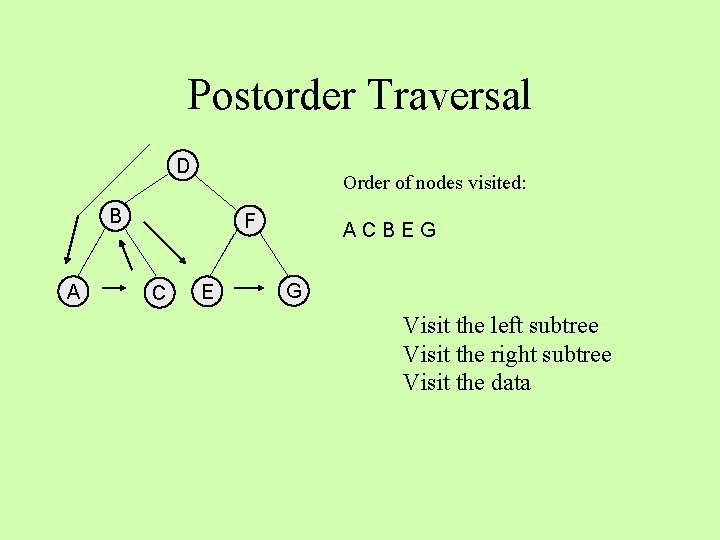
Postorder Traversal D Order of nodes visited: B A F C E ACBE G Visit the left subtree Visit the right subtree Visit the data

Postorder Traversal D Order of nodes visited: B A F C E ACBEG G Visit the left subtree Visit the right subtree Visit the data

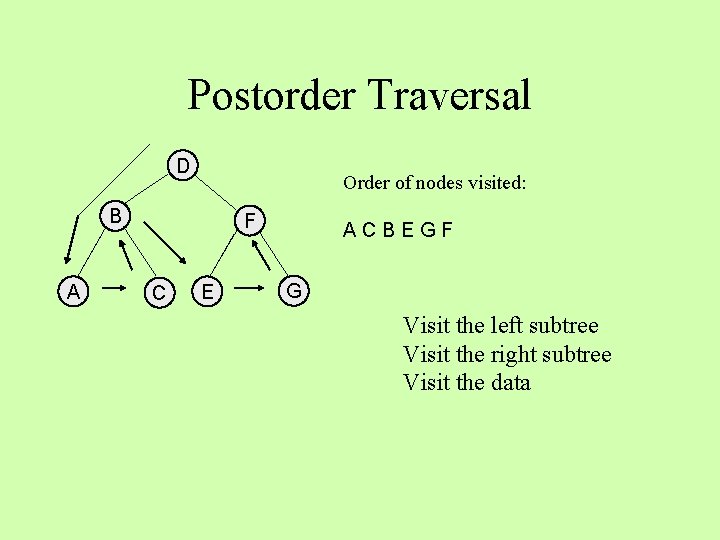
Postorder Traversal D Order of nodes visited: B A F C E ACBEGF G Visit the left subtree Visit the right subtree Visit the data

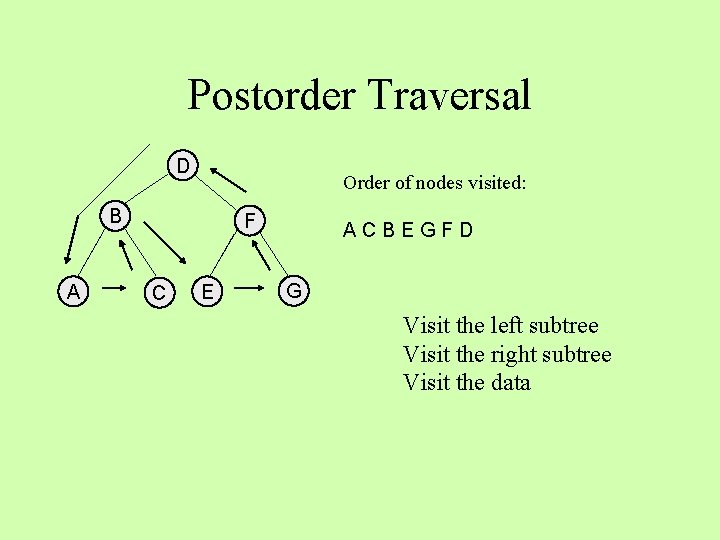
Postorder Traversal D Order of nodes visited: B A F C E ACBEGFD G Visit the left subtree Visit the right subtree Visit the data

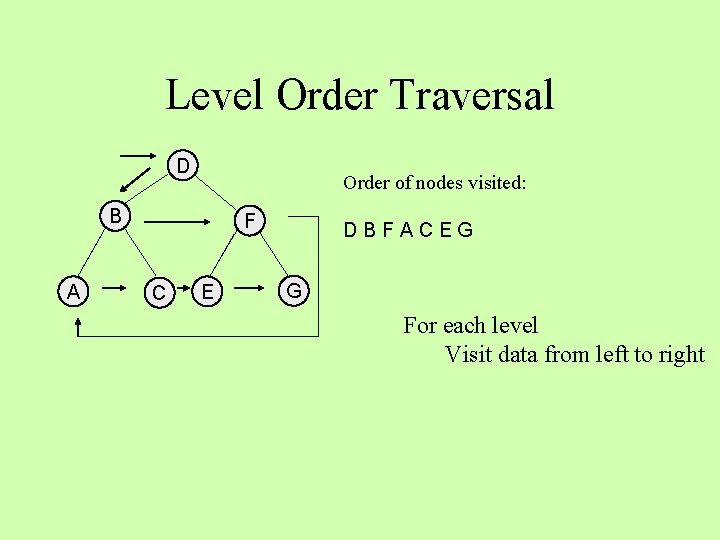
Level Order Traversal D Order of nodes visited: B A F C E DBFACEG G For each level Visit data from left to right

Tree Applications • File directories • Processing sentences (computer programs or natural languages) • Searchable data structures • Heaps (implement heap sort, priority queues)

For Monday Binary Search Trees