Computer Organization Design 5 th Chapter 3 Arithmetic

Computer Organization & Design 5 th. Chapter 3 Arithmetic for Computers 電腦之算術運算 ROBERT CHEN SHU-TE UNIVERSITY CSIE DEPT. 3 -1

Computer Organization & Design 5 th. Outlines • • • Signed and Unsigned Numbers(有號數與無號數) Addition and Subtraction(加法與減法)) Multiplication(乘法) Division(除法) Floating Point(浮點數) SHU-TE UNIVERSITY CSIE DEPT. 3 -2

Computer Organization & Design 5 th. Signed and Unsigned Numbers • Numbers can be presented in any base(基底) – A n-bit number: an-1 an-2…a 1 a 0, base is d, then its decimal value is: an-1× d n-1+ an-2 × d n-2 + … + a 1 × d n-1 + a 0 × d 0 (10) Where a 0 called the Least Significant Bit (LSB最低有效位元), an-1 called the Most Significant Bit (LSB最高有效位元) [Ex] 1011 two = ten ? [Ans] (1 × 23) + (0 × 22) + (1 × 21) + (1 × 20) = (1 × 8) + (0 × 4) + (1 × 2) + (1 × 1) = 8 + 0 + 2 + 1 = 11 ten SHU-TE UNIVERSITY CSIE DEPT. 3 -3

Computer Organization & Design 5 th. Signed and Unsigned Numbers • Negative Number Representation (負數表示法) – Sign-magnitude – 1’s complement – 2’s complement (adopted by all now-a-day computers) • For a n-bit binary number – The Most Significant Bit (MSB) represents the sign : 0 : positive, 1: negative – The rest (n-1) bits represents the magnitude Method comparison SM 1’s 2’s Positive number(正數) sm sm sm Negative number(負數 ) sm sm’ s(m’+1) -(2 n-1 -1) ~ +(2 n-1 -1) -(2 n-1) ~ +(2 n-1 -1) Range Zero representation +0, -0 +0 快速求法：欲求某負數之2’s complement表示法，可先求其正數，再取補數後加 1，注意位元數目 ！ SHU-TE UNIVERSITY CSIE DEPT. 3 -4

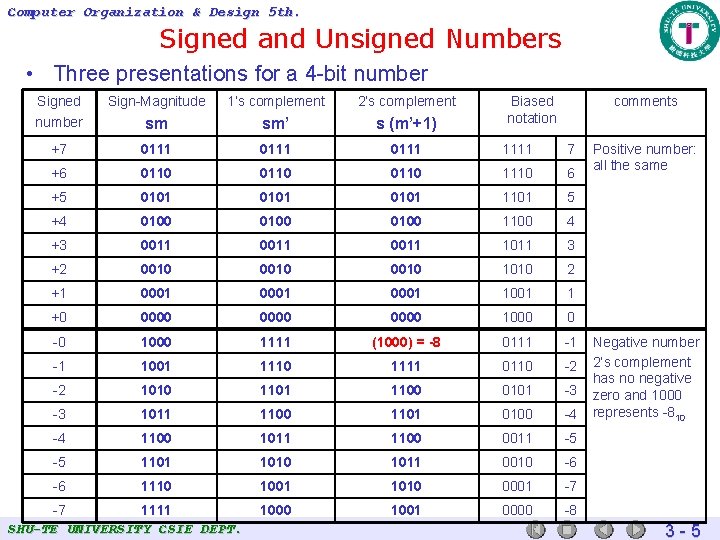
Computer Organization & Design 5 th. Signed and Unsigned Numbers • Three presentations for a 4 -bit number Signed number Sign-Magnitude 1’s complement 2’s complement sm sm’ s (m’+1) +7 0111 1111 7 +6 0110 1110 6 +5 0101 1101 5 +4 0100 1100 4 +3 0011 1011 3 +2 0010 1010 2 +1 0001 1 +0 0000 1000 0 -0 1000 1111 (1000) = -8 0111 -1 -1 1001 1110 1111 0110 -2 -2 1010 1101 1100 0101 -3 -3 1011 1100 1101 0100 -4 -4 1100 1011 1100 0011 -5 -5 1101 1010 1011 0010 -6 -6 1110 1001 1010 0001 -7 1000 1001 0000 -8 -7 1111 SHU-TE UNIVERSITY CSIE DEPT. Biased notation comments Positive number: all the same Negative number 2’s complement has no negative zero and 1000 represents -810 3 -5

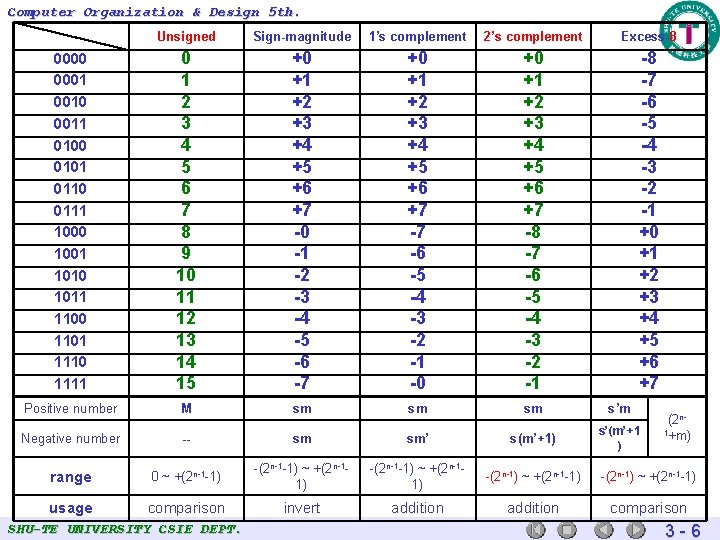
Computer Organization & Design 5 th. Unsigned Sign-magnitude 1’s complement 2’s complement Excess-8 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 +0 +1 +2 +3 +4 +5 +6 +7 -0 -1 -2 -3 -4 -5 -6 -7 +0 +1 +2 +3 +4 +5 +6 +7 -7 -6 -5 -4 -3 -2 -1 -0 +0 +1 +2 +3 +4 +5 +6 +7 -8 -7 -6 -5 -4 -3 -2 -1 +0 +1 +2 +3 +4 +5 +6 +7 Positive number M sm sm sm s’(m’+1 ) (2 n 1+m) Negative number -- sm sm’ s(m’+1) range 0 ~ +(2 n-1 -1) -(2 n-1 -1) ~ +(2 n-11) -(2 n-1) ~ +(2 n-1 -1) usage comparison invert addition comparison SHU-TE UNIVERSITY CSIE DEPT. 3 -6

Computer Organization & Design 5 th. Signed and Unsigned Numbers • 2’s complement binary number to decimal conversion an-1× (-d n-1)+ an-2 × d n-2 + … + a 1 × d n-1 + a 0 × d 0 (10) [Ex] what is the decimal number of the 32 -bit binary pattern? 1111 1111 11002 [Ans] (1×-231) + (1× 230) + (1× 229) + … + (1× 22) + (0× 21) + (0× 20) = - 231 + 230 + 229 + … + 22 + 0 = - 214748364810 + 214748364410 = - 410 [Ex] Find -210 2’s complement representation (1) Find 210 = 0000 0000 00102 (2) Complement : 1111 1111 11012 ＋ (3) Add 1 : 1 2 1111 1111 11102 SHU-TE UNIVERSITY CSIE DEPT. 3 -7

Computer Organization & Design 5 th. Signed and Unsigned Numbers [Ex] Show that a 2’s-complement number can be converted to a representation with more bits by sign extension. That is, given an n-bit 2’s-complement number X, show that the m-bit 2’s-complement representation of X, where m > n, can be obtained by appending m-n copies of X’s sign bit to the left of thze n-bit r e p r e s e n t a t i o n o f X. [ 8 4清 大 電 機] [Ans] 若假設X為n-bit正數，欲做sign extension成A (m-bit)，則將bit n~(m-1)補 0，則 （因為am-1 ~ an-1皆為 0） 若假設X為n-bit負數，欲做sign extension成A (m-bit)， 因為轉換後的A=原來的X值，所以 SHU-TE UNIVERSITY CSIE DEPT. 明顯地，ai(n-1 i m-2)必須全為 1，亦 即將an-1=1做sign extension m-1 n-1 m-n bits 0 n bits 3 -8

Computer Organization & Design 5 th. Signed and Unsigned Numbers [Ex] Let A=an-1 an-2…a 1 a 0 be a two’s complement integer. Show that [Ans] (1)若A為正數，則an-1=0，A=an-1 an-2…a 1 a 0(2)=0 an-2…a 1 a 0(2)= (2)若A為負數，則an-1=1，A=an-1 an-2…a 1 a 0(2)=1 an-2…a 1 a 0(2) 由(1), (2)得證 SHU-TE UNIVERSITY CSIE DEPT. 3 -9

Computer Organization & Design 5 th. Signed and Unsigned Numbers • Sign extension (符號擴展) – Converting n-bit numbers into numbers with more than n bits – copy the most significant bit (the sign bit) into the other bits 0010 -> 0000 0010 1010 -> 1111 1010 • MIPS “data transfer” instruction (load/store) Load word lw $s 1, 100($s 2) $s 1 = M[$s 2+100] Mem. Reg. Store word sw $s 1, 100($s 2) M[$s 2+100] = $s 1 Reg. Mem. Load unsigned half word lhu $s 1, 100($s 2) $s 1 = M[$s 2+100] Mem. Reg. Store half word sh $s 1, 100($s 2) M[$s 2+100] = $s 1 Reg. Mem. Load unsigned byte lbu $s 1, 100($s 2) $s 1 = M[$s 2+100] Mem. Reg. Store byte sb $s 1, 100($s 2) M[$s 2+100] = $s 1 Reg. Mem. Load upper half word immediate lui $s 1, 100 $s 1 = 100 * 216 Mem. Reg. SHU-TE UNIVERSITY CSIE DEPT. 3 -

Computer Organization & Design 5 th. Signed and Unsigned Numbers • Signed vs. unsigned number $s 0 = 1111 11112 $s 1 = 0000 0000 00012 sltu $t 0, $s 1 # signed number comparison $t 1, $s 0, $s 1 # unsigned number comparison After executing the above instructions, $t 0 = 1, $t 1 = 0. Why? • Range detection [Ex] If ($a 1>$a 2) or ($a 1< 0) then jump to Index. Out. Of. Bounds sltu $t 0, $a 1, $t 2 # temp reg $t 0=0, if k>=length or k<0 beq $t 0, zero, Index. Out. Of. Bounds # if exceed, then jump SHU-TE UNIVERSITY CSIE DEPT. 3 -

Computer Organization & Design 5 th. Signed and Unsigned Numbers [Ex 1] Write all 4 -bit numbers using the above representations. (1) according the decimal number (2) according the 0000 ~ 1111 (3) compare their range and zero representation, max/min number [Ex 2] Show -18 using the above representations with (1) 8 bits (2) 16 bits. [Ans] sign-magnitude: 1’s complement: 2’s complement: 10010010 11101101 1110 1000 0001 0010 1111 1110 1101 1111 1110 [Ex 3] Why 2’s complement representation is better than the others in computer architecture? [Ans] 1. One representation of zero 2. Arithmetic works easily 3. Negating is fairly easy [Ex 4] What is overflow ? How to judge whether an overflow happens or not? Cin Cout =1 [Ex 5] Express +69 and -69 with 8 bits using signed-magnitude, 1’s complement, 2’s complement and excess code representations. [Ans] sign-magnitude 0100 01011100 0101 1’s complement 0100 01011011 1010 2’s complement 0100 01011011 excess-128 code 1100 01010011 1011 SHU-TE UNIVERSITY CSIE DEPT. 3 -

Computer Organization & Design 5 th. Effects of Overflow • An exception (interrupt) occurs – Control jumps to predefined address for exception – Interrupted address is saved for possible resumption • Don't always want to detect overflow – addu, addiu, subu do NOT cause exceptions on overflow note: addiu still sign-extends! note: sltu, sltiu for unsigned comparisons – add, addi, sub cause exceptions on overflow • MIPS C compiler 總是產生無號數之算術指令所以會忽略溢位， 但MIPS FORTRAN compiler則會依據運算元型態產生適當的 算術指令 • 自行研究課本p. 173, 174之程式 SHU-TE UNIVERSITY CSIE DEPT. 3 -

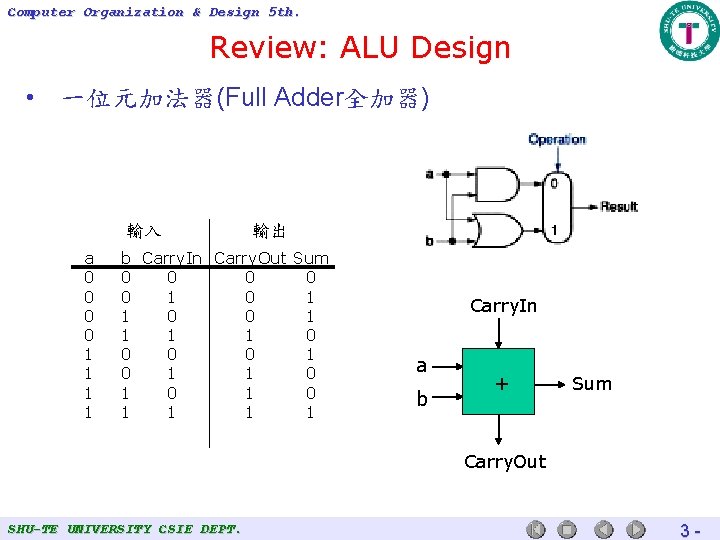
Computer Organization & Design 5 th. Review: ALU Design • 一位元加法器(Full Adder全加器) 輸入 a 0 0 1 1 輸出 b Carry. In Carry. Out Sum 0 0 0 1 1 0 0 1 0 1 0 1 1 1 1 Carry. In a b + Sum Carry. Out SHU-TE UNIVERSITY CSIE DEPT. 3 -

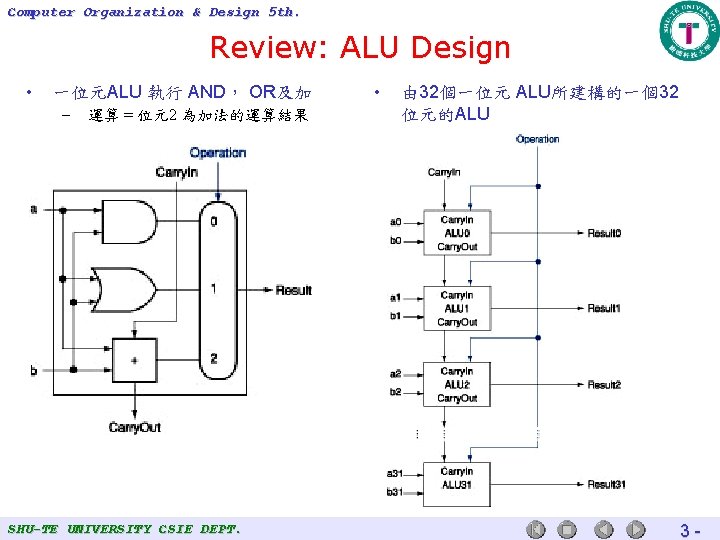
Computer Organization & Design 5 th. Review: ALU Design • 一位元ALU 執行 AND， OR及加 – 運算 = 位元2 為加法的運算結果 SHU-TE UNIVERSITY CSIE DEPT. • 由 32個一位元 ALU所建構的一個32 位元的ALU 3 -

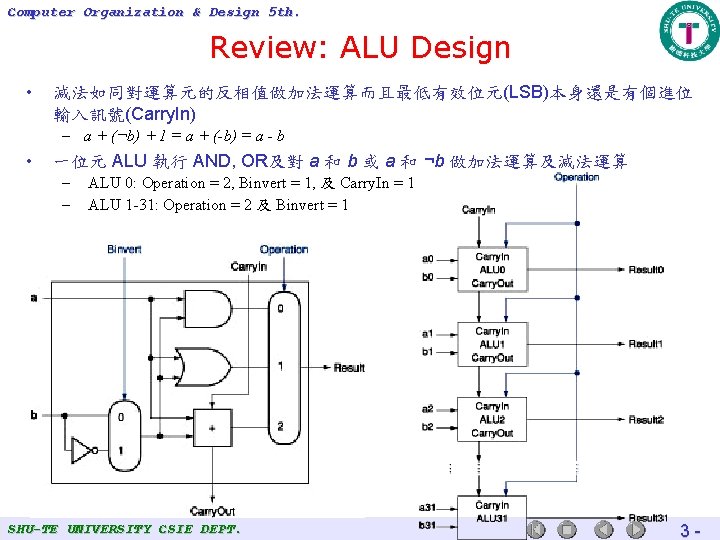
Computer Organization & Design 5 th. Review: ALU Design • 減法如同對運算元的反相值做加法運算而且最低有效位元(LSB)本身還是有個進位 輸入訊號(Carry. In) – a + (¬b) + 1 = a + (-b) = a - b • 一位元 ALU 執行 AND, OR及對 a 和 b 或 a 和 ¬b 做加法運算及減法運算 – ALU 0: Operation = 2, Binvert = 1, 及 Carry. In = 1 – ALU 1 -31: Operation = 2 及 Binvert = 1 SHU-TE UNIVERSITY CSIE DEPT. 3 -

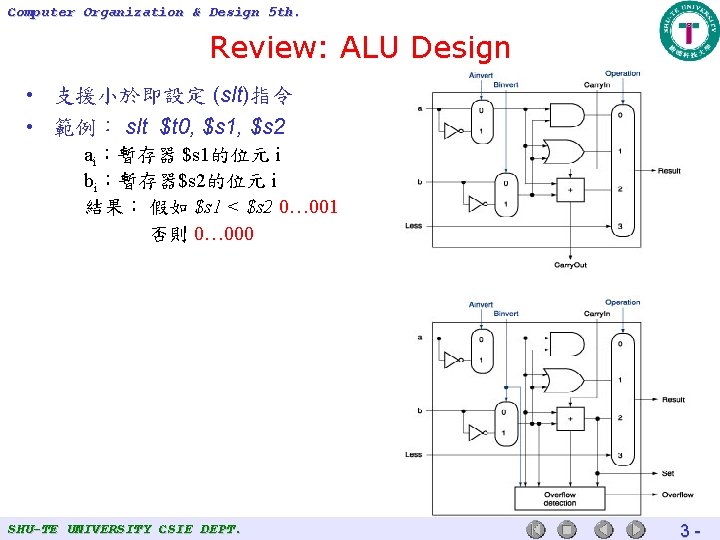
Computer Organization & Design 5 th. Review: ALU Design • 支援小於即設定 (slt)指令 • 範例： slt $t 0, $s 1, $s 2 ai：暫存器 $s 1的位元 i bi：暫存器$s 2的位元 i 結果： 假如 $s 1 < $s 2 0… 001 否則 0… 000 SHU-TE UNIVERSITY CSIE DEPT. 3 -

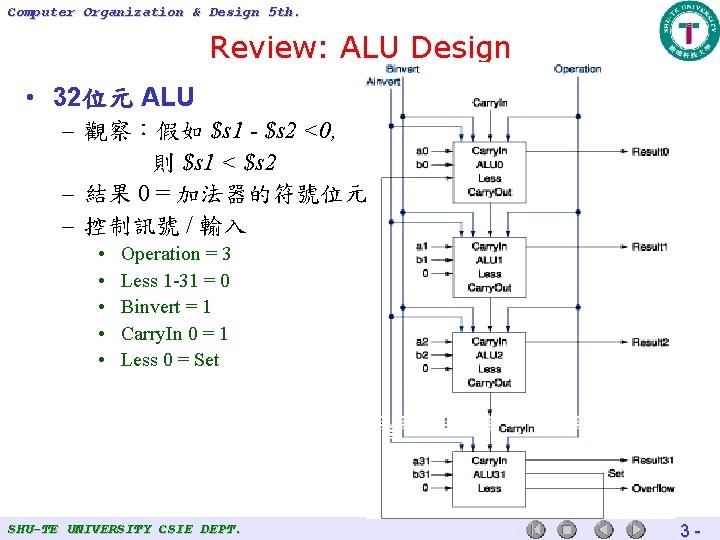
Computer Organization & Design 5 th. Review: ALU Design • 32位元 ALU – 觀察：假如 $s 1 - $s 2 <0, 則 $s 1 < $s 2 – 結果 0 = 加法器的符號位元 – 控制訊號 / 輸入 • • • Operation = 3 Less 1 -31 = 0 Binvert = 1 Carry. In 0 = 1 Less 0 = Set SHU-TE UNIVERSITY CSIE DEPT. 3 -

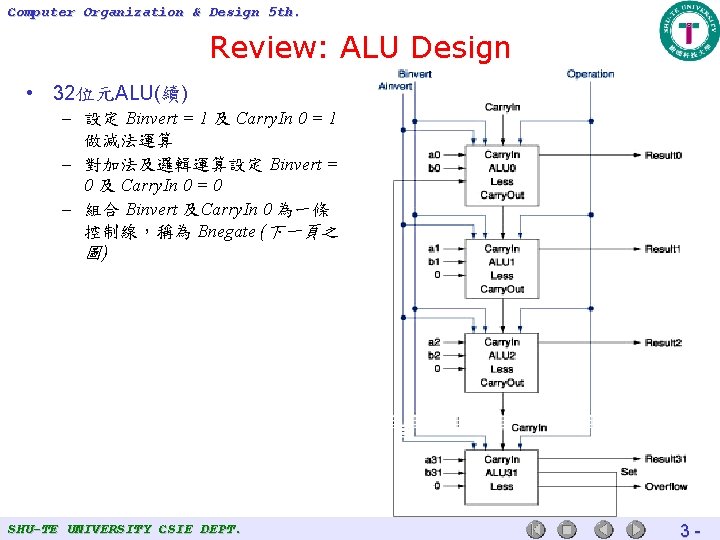
Computer Organization & Design 5 th. Review: ALU Design • 32位元ALU(續) – 設定 Binvert = 1 及 Carry. In 0 = 1 做減法運算 – 對加法及邏輯運算設定 Binvert = 0 及 Carry. In 0 = 0 – 組合 Binvert 及Carry. In 0 為一條 控制線，稱為 Bnegate (下一頁之 圖) SHU-TE UNIVERSITY CSIE DEPT. 3 -

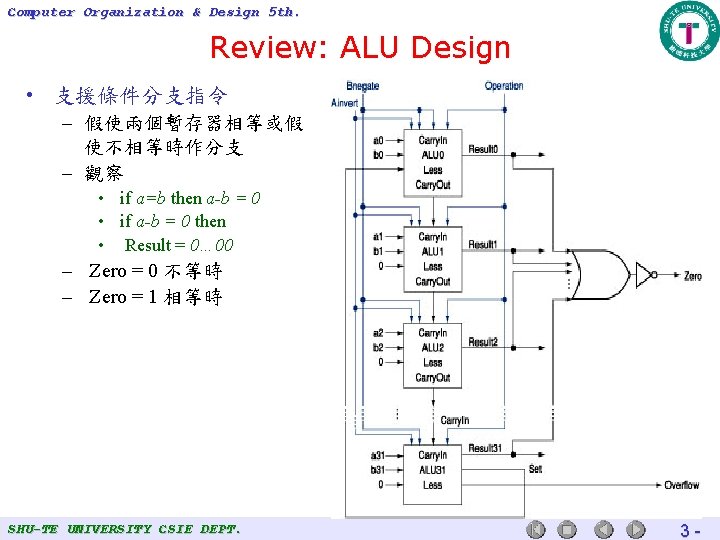
Computer Organization & Design 5 th. Review: ALU Design • 支援條件分支指令 – 假使兩個暫存器相等或假 使不相等時作分支 – 觀察 • if a=b then a-b = 0 • if a-b = 0 then • Result = 0… 00 – Zero = 0 不等時 – Zero = 1 相等時 SHU-TE UNIVERSITY CSIE DEPT. 3 -

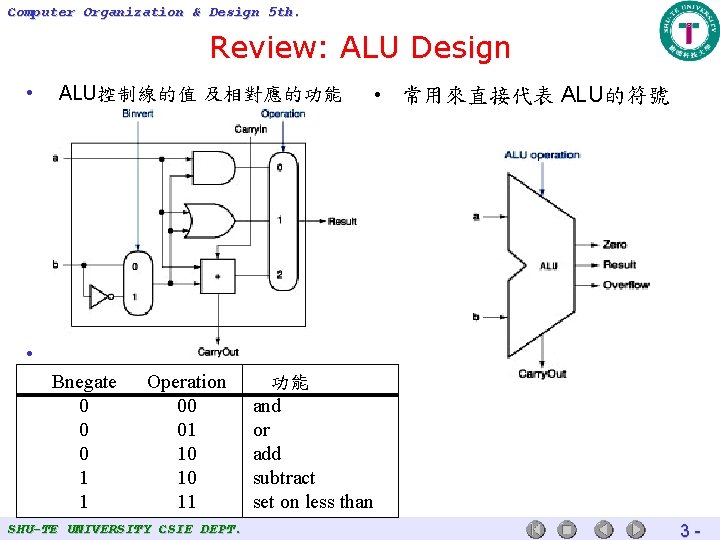
Computer Organization & Design 5 th. Review: ALU Design • ALU控制線的值 及相對應的功能 • 常用來直接代表 ALU的符號 • Bnegate 0 0 0 1 1 Operation 00 01 10 10 11 SHU-TE UNIVERSITY CSIE DEPT. 功能 and or add subtract set on less than 3 -

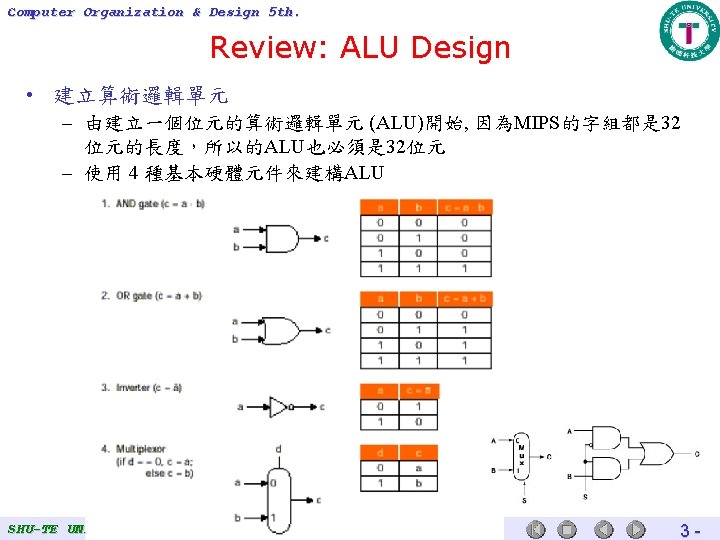
Computer Organization & Design 5 th. Review: ALU Design • We can build an ALU to support the MIPS instruction set – key idea: use multiplexer (MUX) to select the output we want – efficiently perform subtraction using two’s complement – replicate a 1 -bit ALU to produce a 32 -bit ALU • Important points about hardware – all of the gates are always working – the speed of a gate is affected by the number of inputs to the gate – the speed of a circuit is affected by the number of gates in series (on the “critical path” or the “deepest level of logic”) SHU-TE UNIVERSITY CSIE DEPT. 3 -

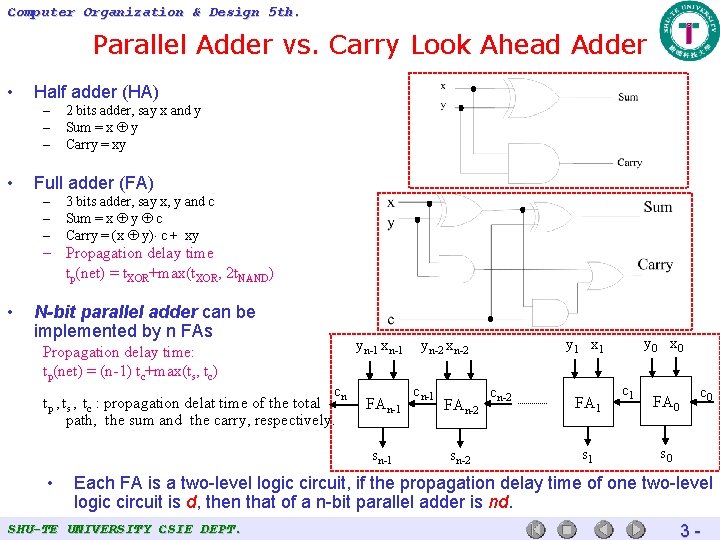
Computer Organization & Design 5 th. Parallel Adder vs. Carry Look Ahead Adder • Half adder (HA) – – – • 2 bits adder, say x and y Sum = x y Carry = xy Full adder (FA) – – – 3 bits adder, say x, y and c Sum = x y c Carry = (x y) c + xy – Propagation delay time tp(net) = t. XOR+max(t. XOR, 2 t. NAND) • N-bit parallel adder can be implemented by n FAs Propagation delay time: tp(net) = (n-1) tc+max(ts, tc) c tp , ts , tc : propagation delat time of the total n path, the sum and the carry, respectively. yn-1 xn-1 FAn-1 sn-1 • cn-1 FAn-2 sn-2 y 0 x 0 y 1 x 1 yn-2 xn-2 cn-2 FA 1 s 1 c 1 FA 0 c 0 s 0 Each FA is a two-level logic circuit, if the propagation delay time of one two-level logic circuit is d, then that of a n-bit parallel adder is nd. SHU-TE UNIVERSITY CSIE DEPT. 3 -

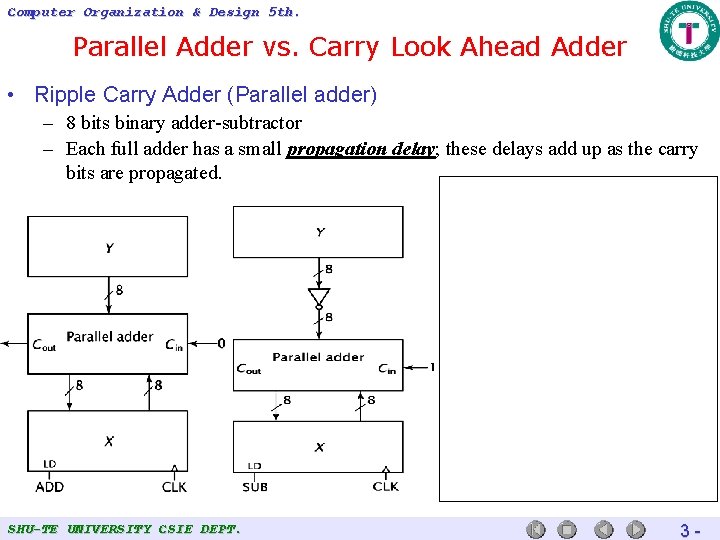
Computer Organization & Design 5 th. Parallel Adder vs. Carry Look Ahead Adder • Ripple Carry Adder (Parallel adder) – 8 bits binary adder-subtractor – Each full adder has a small propagation delay; these delays add up as the carry bits are propagated. SHU-TE UNIVERSITY CSIE DEPT. 3 -

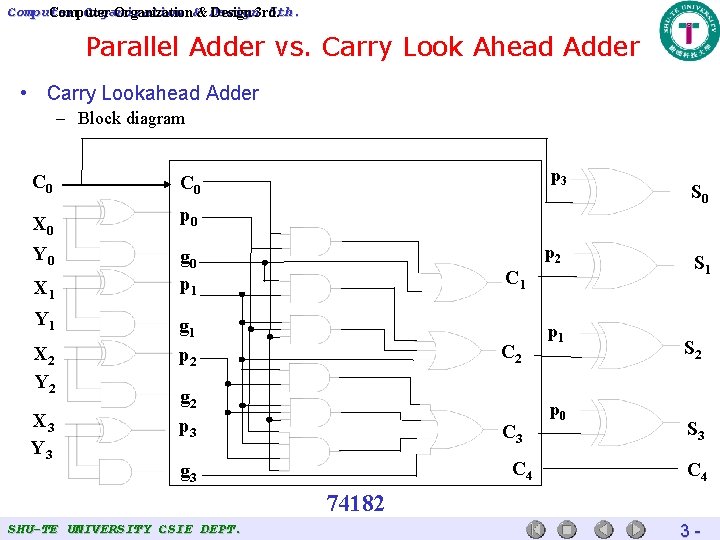
Computer Organization 5 th. Computer Organization&& Design 3 rd. Parallel Adder vs. Carry Look Ahead Adder • Carry Lookahead Adder (4 bits) – One solution to the delay problem – The generate part , g, g = X Y (carry generator) – The second part is the propagate, p, p = X Y (carry propagation) – In general, this can be expressed by the equation Si = P i C i Ci+1 = gi + pi. Ci – For the 4 -bit adder, these values are SHU-TE UNIVERSITY CSIE DEPT. 3 -

Computer Organization 5 th. Computer Organization&& Design 3 rd. Parallel Adder vs. Carry Look Ahead Adder • Carry Lookahead Adder – Block diagram C 0 X 0 Y 0 p 0 X 1 Y 1 X 2 Y 2 X 3 Y 3 p 2 g 0 p 1 C 1 g 1 p 2 C 2 g 2 p 3 C 4 g 3 p 1 p 0 S 1 S 2 S 3 C 4 74182 SHU-TE UNIVERSITY CSIE DEPT. 3 -

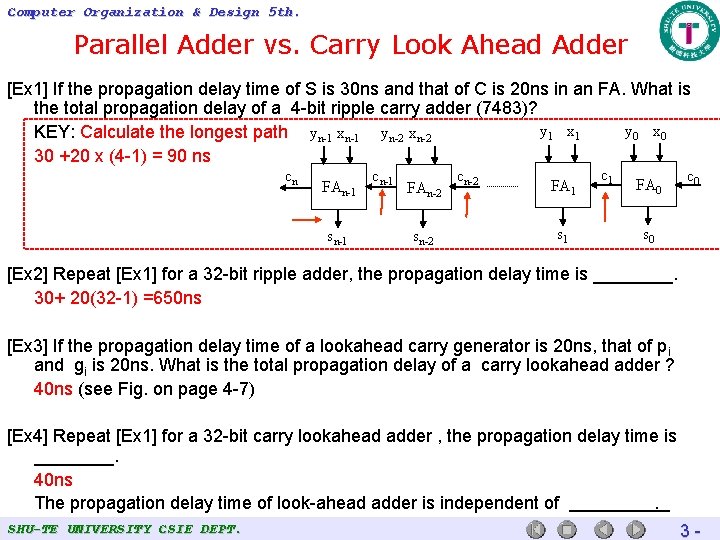
Computer Organization & Design 5 th. Parallel Adder vs. Carry Look Ahead Adder [Ex 1] If the propagation delay time of S is 30 ns and that of C is 20 ns in an FA. What is the total propagation delay of a 4 -bit ripple carry adder (7483)? y 0 x 0 y 1 x 1 KEY: Calculate the longest path yn-1 xn-1 yn-2 xn-2 30 +20 x (4 -1) = 90 ns cn FAn-1 sn-1 cn-1 FAn-2 sn-2 cn-2 FA 1 s 1 c 1 FA 0 c 0 s 0 [Ex 2] Repeat [Ex 1] for a 32 -bit ripple adder, the propagation delay time is ____. 30+ 20(32 -1) =650 ns [Ex 3] If the propagation delay time of a lookahead carry generator is 20 ns, that of p i and gi is 20 ns. What is the total propagation delay of a carry lookahead adder ? 40 ns (see Fig. on page 4 -7) [Ex 4] Repeat [Ex 1] for a 32 -bit carry lookahead adder , the propagation delay time is ____. 40 ns The propagation delay time of look-ahead adder is independent of. SHU-TE UNIVERSITY CSIE DEPT. 3 -

Computer Organization & Design 5 th. Multiplication • Unsigned Integer multiplication(無號整數相乘) • 範例 ． (1000)10 x (1011)10: 1000 x 1011 1000_ 0000__ 1000___ 1011000 SHU-TE UNIVERSITY CSIE DEPT. • Example. (0010)2 x (0011)2: multiplicand被乘數 multiplier乘數 0010 x 0011 0010_ 0000___ 0000110 3 -

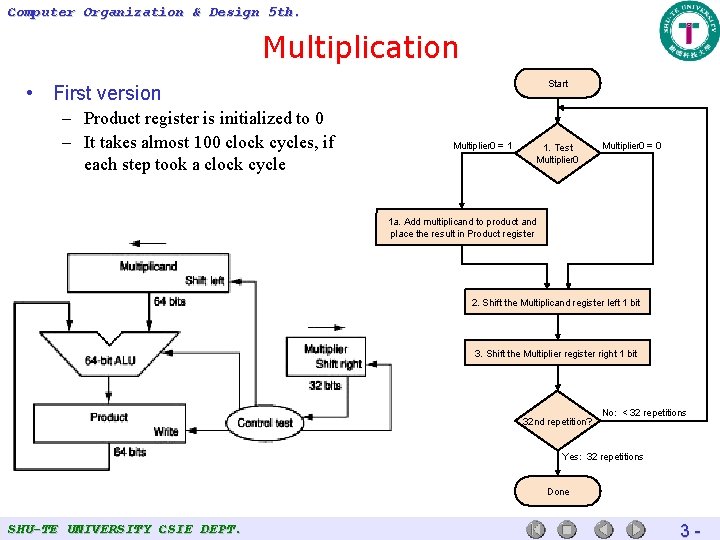
Computer Organization & Design 5 th. Multiplication Start • First version – Product register is initialized to 0 – It takes almost 100 clock cycles, if each step took a clock cycle Multiplier 0 = 1 1. Test Multiplier 0 = 0 1 a. Add multiplicand to product and place the result in Product register 2. Shift the Multiplicand register left 1 bit 3. Shift the Multiplier register right 1 bit 32 nd repetition? No: < 32 repetitions Yes: 32 repetitions Done SHU-TE UNIVERSITY CSIE DEPT. 3 -

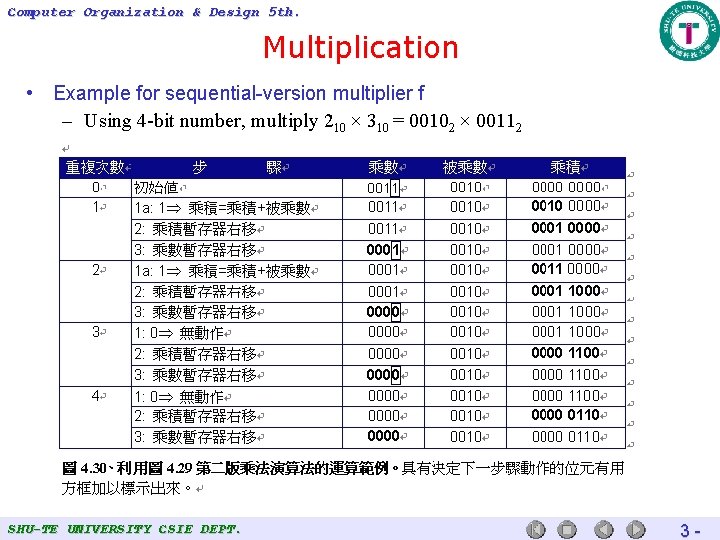
Computer Organization & Design 5 th. Multiplication • Example for first-version multiplier f – Using 4 -bit number, multiply 210 × 310 = 00102 × 00112 SHU-TE UNIVERSITY CSIE DEPT. 3 -

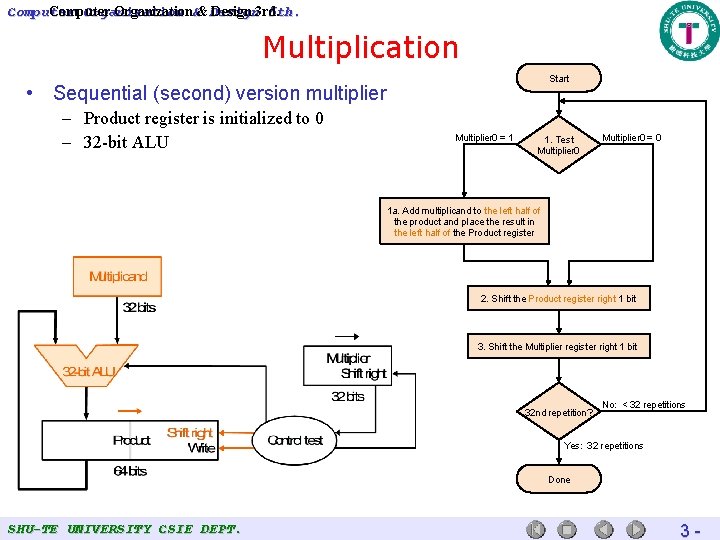
Computer Organization 5 th. Computer Organization&& Design 3 rd. Multiplication Start • Sequential (second) version multiplier – Product register is initialized to 0 – 32 -bit ALU Multiplier 0 = 1 1. Test Multiplier 0 = 0 1 a. Add multiplicand to the left half of the product and place the result in the left half of the Product register 2. Shift the Product register right 1 bit 3. Shift the Multiplier register right 1 bit 32 nd repetition? No: < 32 repetitions Yes: 32 repetitions Done SHU-TE UNIVERSITY CSIE DEPT. 3 -

Computer Organization & Design 5 th. Multiplication • Example for sequential-version multiplier f – Using 4 -bit number, multiply 210 × 310 = 00102 × 00112 SHU-TE UNIVERSITY CSIE DEPT. 3 -

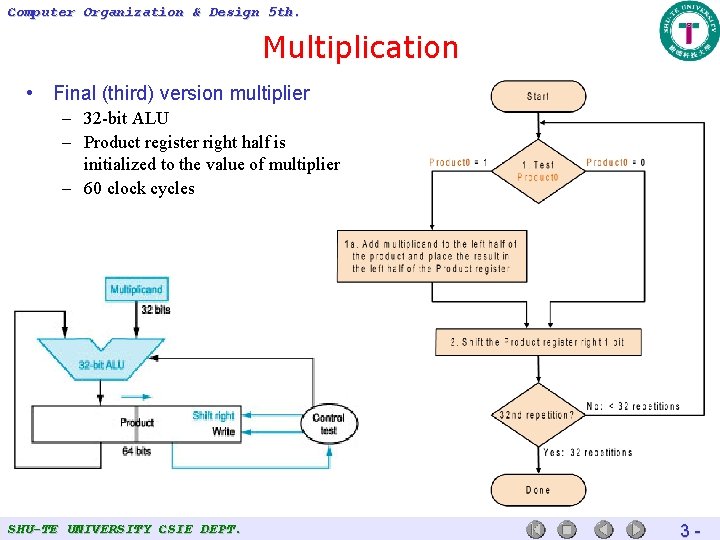
Computer Organization & Design 5 th. Multiplication • Final (third) version multiplier – 32 -bit ALU – Product register right half is initialized to the value of multiplier – 60 clock cycles SHU-TE UNIVERSITY CSIE DEPT. 3 -

Computer Organization 5 th. Computer Organization&& Design 3 rd. Multiplication • Signed Multiplication(有號數乘法) – Convert the multiplier and multiplicand to positive numbers and remember the original signs. – Shifting steps need to extend the sign of the product – Negate the product if the original signs disagree. [NOTE] 有號數乘法：利用第三版乘法器先做前面 31位元的運算，再比較乘 數及被乘數的符號(第 32位元)是否相同 – A more elegant method: Booth’s algorithm • 對有連續1的乘數可加速處理 • 碰到第一個1加法變減法 SHU-TE UNIVERSITY CSIE DEPT. 3 -

Computer Organization 5 th. Computer Organization&& Design 3 rd. Booth’s Algorithm • Classifying groups of bits into the beginning, the middle or the end of a run of 1 s Middle of Run End of Run 0 1 1 1 0 Beginning of Run • Take a look at 2 -bit groups SHU-TE UNIVERSITY CSIE DEPT. 3 -

Computer Organization 5 th. Computer Organization&& Design 3 rd. Booth’s Algorithm • Depending on the current and previous bits, do one of the following: – 00: no arithmetic operation – 01: End of a string of 1 s, so add multiplicand to the left half of the product – 10: Beginning of a strings of 1 s, so subtract the multiplicand from the left half of the product – 11: no arithmetic operation • Shift the Product register right 1 bit. SHU-TE UNIVERSITY CSIE DEPT. 3 -

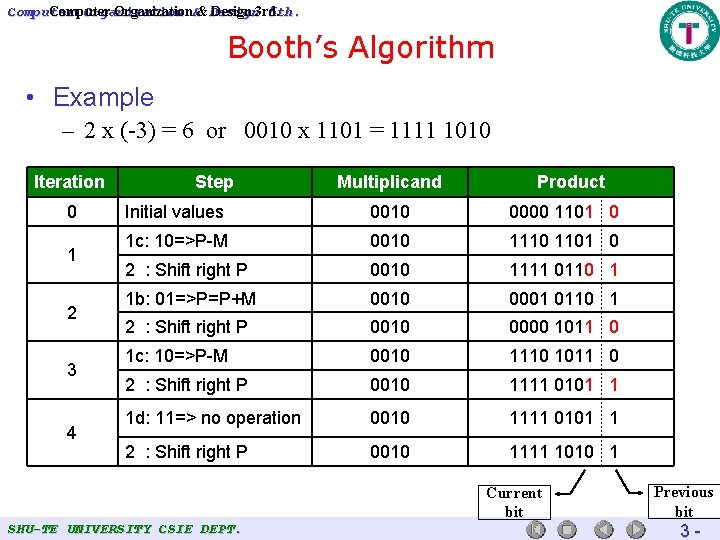
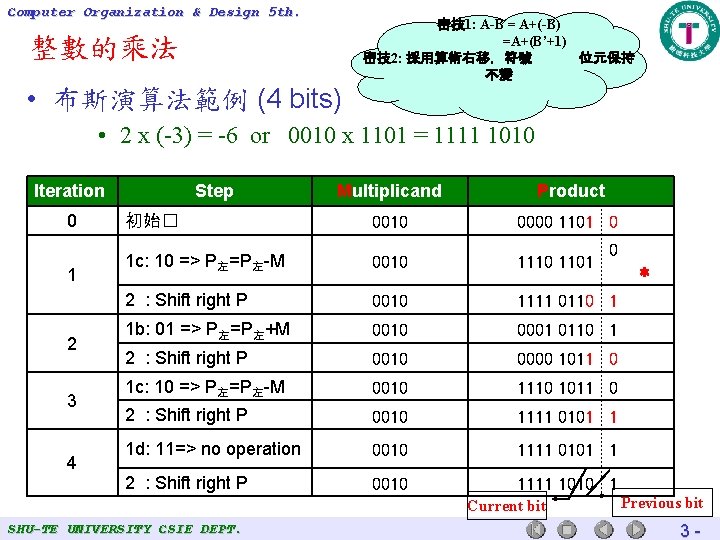
Computer Organization 5 th. Computer Organization&& Design 3 rd. Booth’s Algorithm • Example – 2 x (-3) = 6 or 0010 x 1101 = 1111 1010 Iteration 0 1 2 3 4 Step Multiplicand Product Initial values 0010 0000 1101 0 1 c: 10=>P-M 0010 1101 0 2 : Shift right P 0010 1111 0110 1 1 b: 01=>P=P+M 0010 0001 0110 1 2 : Shift right P 0010 0000 1011 0 1 c: 10=>P-M 0010 1110 1011 0 2 : Shift right P 0010 1111 0101 1 1 d: 11=> no operation 0010 1111 0101 1 2 : Shift right P 0010 1111 1010 1 Current bit SHU-TE UNIVERSITY CSIE DEPT. Previous bit 3 -

Computer Organization & Design 5 th. Booth’s Algorithm • Multiply by 2 i via shift – Shift left by one bit --> multiply by 2 – Shift left by n bit --> multiply by 2 n – Proof of Booth’s Algorithm • Why does it work for 2’s complement signed number? • In other words, if (ai-1 - ai) – = 0 do nothing – = 1 add b – = -1 subtract b • Booth’s algorithm can be written as: (a-1 - a 0) x b x 2 0 + (a 0 - a 1) x b x 2 1 +… +(a 30 -a 31)x b x 2 31 = … = b x a SHU-TE UNIVERSITY CSIE DEPT. 3 -

Computer Organization & Design 5 th. 密技1: A-B = A+(-B) =A+(B’+1) 密技2: 採用算術右移，符號 位元保持 不變 整數的乘法 • 布斯演算法範例 (4 bits) • 2 x (-3) = -6 or 0010 x 1101 = 1111 1010 Iteration 0 1 2 3 4 Step Multiplicand Product 初始� 0010 0000 1101 0 1 c: 10 => P左=P左-M 0010 1101 2 : Shift right P 0010 1111 0110 1 1 b: 01 => P左=P左+M 0010 0001 0110 1 2 : Shift right P 0010 0000 1011 0 1 c: 10 => P左=P左-M 0010 1110 1011 0 2 : Shift right P 0010 1111 0101 1 1 d: 11=> no operation 0010 1111 0101 1 2 : Shift right P 0010 1111 1010 1 Current bit SHU-TE UNIVERSITY CSIE DEPT. 0 ＊ Previous bit 3 -

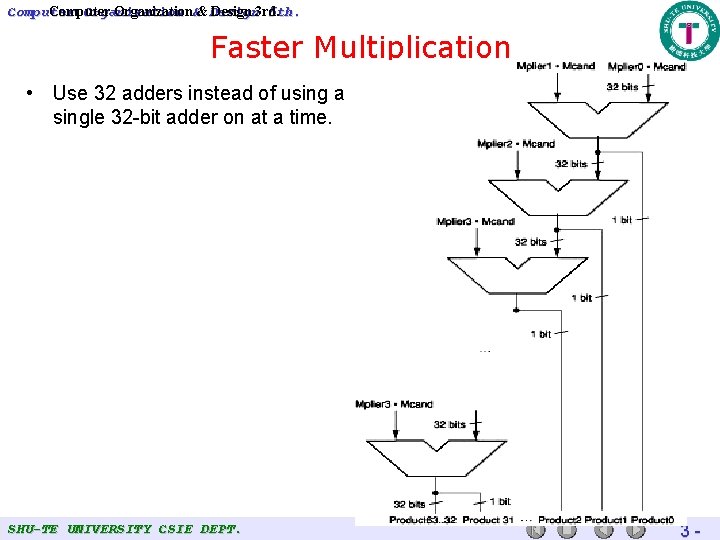
Computer Organization 5 th. Computer Organization&& Design 3 rd. Faster Multiplication • Use 32 adders instead of using a single 32 -bit adder on at a time. SHU-TE UNIVERSITY CSIE DEPT. 3 -

Computer Organization 5 th. Computer Organization&& Design 3 rd. Division • Some definitions: – Dividend(被除數), Divisor(除數), Quotient(商數), Remainder(餘數) – Dividend = Quotient × Divisor + Remainder • Example: 1001010 divided by 1000 Divisor 1000 SHU-TE UNIVERSITY CSIE DEPT. 1001 Quotient(商) 1001010 Dividend(被除數) – 1000 10 1010 – 1000 10 Remainder (or Modulo result) 3 -

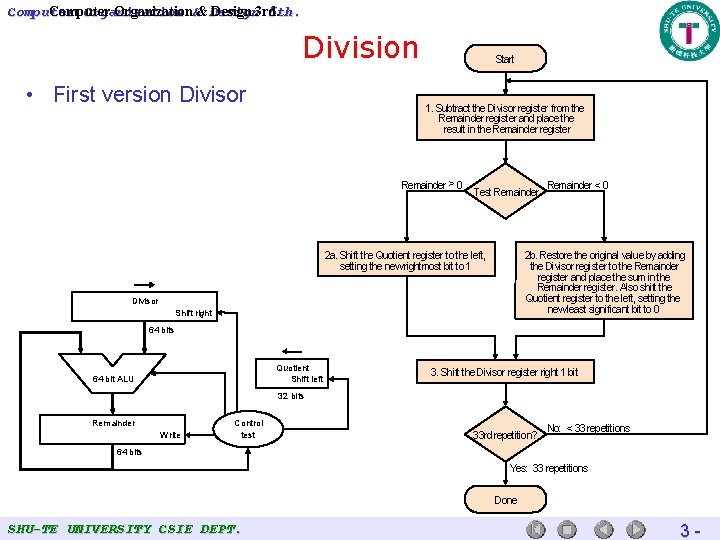
Computer Organization 5 th. Computer Organization&& Design 3 rd. Division • First version Divisor Start 1. Subtract the Divisor register from the Remainder register and place the result in the Remainder register Remainder > 0 Test Remainder 2 a. Shift the Quotient register to the left, setting the new rightmost bit to 1 Remainder < 0 2 b. Restore the original value by adding the Divisor register to the Remainder register and place the sum in the Remainder register. Also shift the Quotient register to the left, setting the new least significant bit to 0 Divisor Shift right 64 bits Quotient Shift left 64 -bit ALU 3. Shift the Divisor register right 1 bit 32 bits Remainder Write Control test 33 rd repetition? No: < 33 repetitions 64 bits Yes: 33 repetitions Done SHU-TE UNIVERSITY CSIE DEPT. 3 -

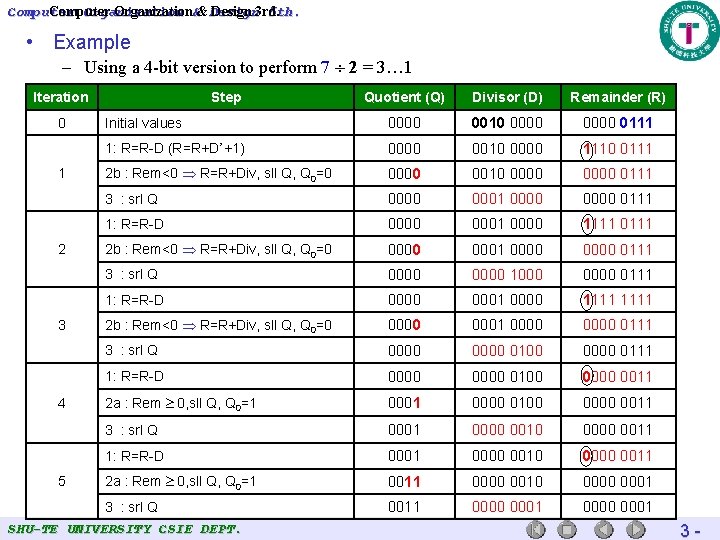
Computer Organization 5 th. Computer Organization&& Design 3 rd. • Example – Using a 4 -bit version to perform 7 2 = 3… 1 Iteration 0 1 2 3 4 5 Step Quotient (Q) Divisor (D) Remainder (R) Initial values 0000 0010 0000 0111 1: R=R-D (R=R+D’+1) 0000 0010 0000 1110 0111 2 b : Rem<0 R=R+Div, sll Q, Q 0=0 0000 0010 0000 0111 3 : srl Q 0000 0001 0000 0111 1: R=R-D 0000 0001 0000 1111 0111 2 b : Rem<0 R=R+Div, sll Q, Q 0=0 0001 0000 0111 3 : srl Q 0000 1000 0111 1: R=R-D 0000 0001 0000 1111 2 b : Rem<0 R=R+Div, sll Q, Q 0=0 0001 0000 0111 3 : srl Q 0000 0100 0000 0111 1: R=R-D 0000 0100 0011 2 a : Rem 0, sll Q, Q 0=1 0000 0100 0011 3 : srl Q 0001 0000 0010 0000 0011 1: R=R-D 0001 0000 0010 0000 0011 2 a : Rem 0, sll Q, Q 0=1 0011 0000 0010 0001 3 : srl Q 0011 0000 0001 SHU-TE UNIVERSITY CSIE DEPT. 3 -

Computer Organization & Design 5 th. Division • Observations on the first version of the division hardware – 1/2 bits in divisor always 0 • 1/2 of 64 -bit adder is wasted • 1/2 of divisor is wasted – Instead of shifting divisor to right, shift remainder to left? – 1 st step cannot produce a 1 in quotient bit (otherwise too big) • switch order to shift first and then subtract, can save 1 iteration SHU-TE UNIVERSITY CSIE DEPT. 3 -

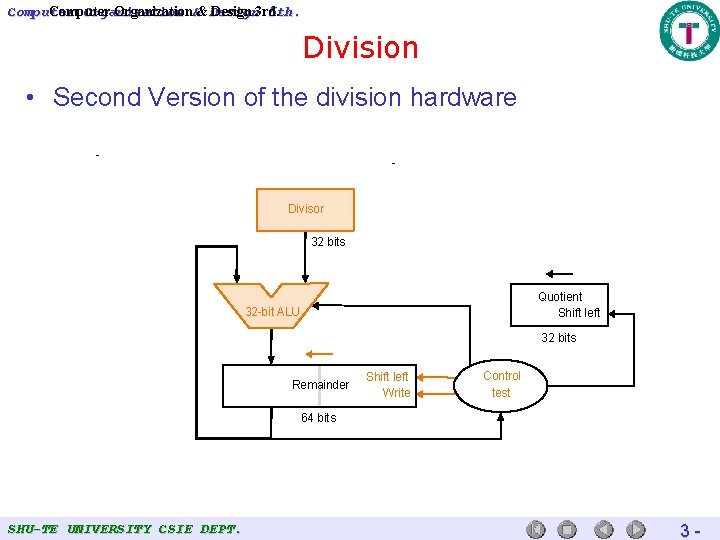
Computer Organization 5 th. Computer Organization&& Design 3 rd. Division • Second Version of the division hardware Divisor 32 bits Quotient Shift left 32 -bit ALU 32 bits Remainder Shift left Write Control test 64 bits SHU-TE UNIVERSITY CSIE DEPT. 3 -

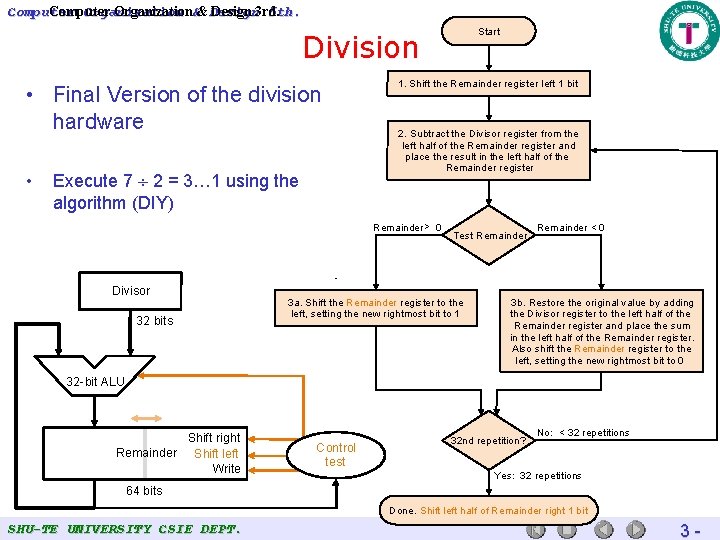
Computer Organization 5 th. Computer Organization&& Design 3 rd. Start Division • Final Version of the division hardware • Execute 7 2 = 3… 1 using the algorithm (DIY) 1. Shift the Remainder register left 1 bit 2. Subtract the Divisor register from the left half of the Remainder register and place the result in the left half of the Remainder register Remainder > 0 Divisor 32 bits Test Remainder 3 a. Shift the Remainder register to the left, setting the new rightmost bit to 1 Remainder < 0 3 b. Restore the original value by adding the Divisor register to the left half of the Remainder register and place the sum in the left half of the Remainder register. Also shift the Remainder register to the left, setting the new rightmost bit to 0 32 -bit ALU Shift right Remainder Shift left Write Control test 32 nd repetition? No: < 32 repetitions Yes: 32 repetitions 64 bits Done. Shift left half of Remainder right 1 bit SHU-TE UNIVERSITY CSIE DEPT. 3 -

Computer Organization 5 th. Computer Organization&& Design 3 rd. Division • Signed Division(有號數除法) – Dividend = Quotient * Divisor + Remainder – Consider the signs of dividend and divisor : 7 2 • • +7 +2 = +3 … +1 -7 +2 = (-3) … (-1) +7 -2 = (-3) … +1 -7 -2 = +3 … (-1) 7 = (+3) × 2 + 1 - 7 = (-3) × 2 + (-1) 7 = (-3) × (-2) + 1 - 7 = (+3) × (-2) + (-1) – Correctly signed division algorithm • If the signs of the operands are opposite – negative the Quotient – make the sign of the nonzero Remainder match the Dividend • 除法運算元異號時，商數取負號，非零餘數與除數同號 SHU-TE UNIVERSITY CSIE DEPT. 3 -

Computer Organization 5 th. Computer Organization&& Design 3 rd. Floating Point • IEEE 754 – 表示形式：(-1)s × (1. m) * 2 e – 格式： Single precision (單精度): 4 bytes : (S, E, M) = (1, 8, 23) , 指數: 超27 -1 Double precision (倍精度): 8 bytes : (S, E, M) = (1, 11, 52) , 指數: 超210 -1 ？？ precision (雙倍精度): 16 bytes : (S, E, M) = (1, 15, 112) , 指數: 超214 -1 – 轉換步驟(單精度) • 轉換成二進位數(-1)s × (1. m) * 2 e • E = e + 127 = 2 （轉成二進位，一定只有8 bits） • 寫答案(SEM) SHU-TE UNIVERSITY CSIE DEPT. 3 -

Computer Organization & Design 5 th. 浮點數範例 [範例]用IEEE 754浮點數表示-10. 0312510，格式為(S, E, M)=(1, 8, 23) 解答: 1. 一律先以正數轉換成二進位數 10. 03125 10= 1010. 000012 = 1. 01000001 23 (這時還不要加負號) m=010000010… 0 , (共 15個0) e = 3 2. E = e + (28 -1 -1) = 2 （轉成二進位，一定只有8 bits） E = 3 + 127 = 130 10 = 10000010 2 3. 寫答案(SEM)，此時才依據正負號填入S S E M 1 10000010 010000… 0 (共 12個0) 4. 轉成十六進位 110000010 010000… 0 2 = C 120800016 Youtube影片 IEEE 754轉換 SHU-TE UNIVERSITY CSIE DEPT. 3 -

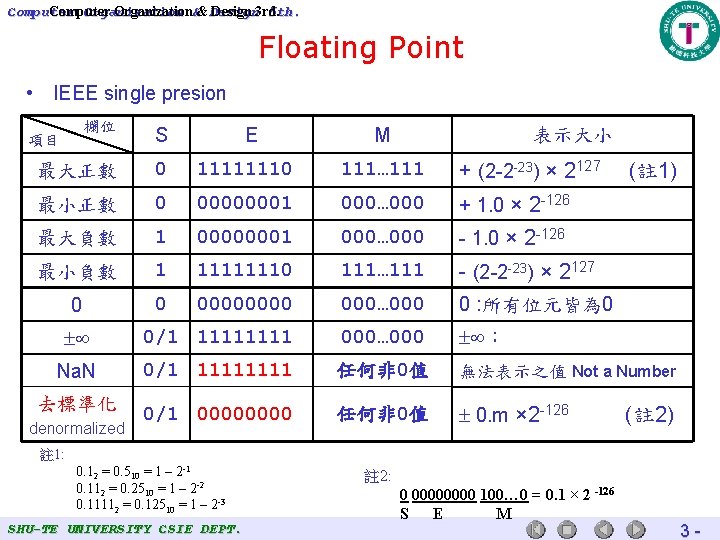
Computer Organization 5 th. Computer Organization&& Design 3 rd. Floating Point • IEEE single presion 欄位 S 最大正數 0 11111110 111… 111 + (2 -2 -23) × 2127 最小正數 0 00000001 000… 000 + 1. 0 × 2 -126 最大負數 1 00000001 000… 000 - 1. 0 × 2 -126 最小負數 1 11111110 111… 111 - (2 -2 -23) × 2127 0 0 0000 000… 000 0 : 所有位元皆為 0 0/1 1111 000… 000 ： Na. N 0/1 1111 任何非 0值 無法表示之值 Not a Number 去標準化 0/1 0000 任何非 0值 0. m × 2 -126 項目 denormalized E M 表示大小 (註 1) (註 2) 註 1: 0. 12 = 0. 510 = 1 – 2 -1 0. 112 = 0. 2510 = 1 – 2 -2 0. 11112 = 0. 12510 = 1 – 2 -3 SHU-TE UNIVERSITY CSIE DEPT. 註 2: 0 0000 100… 0 = 0. 1 × 2 -126 S E M 3 -

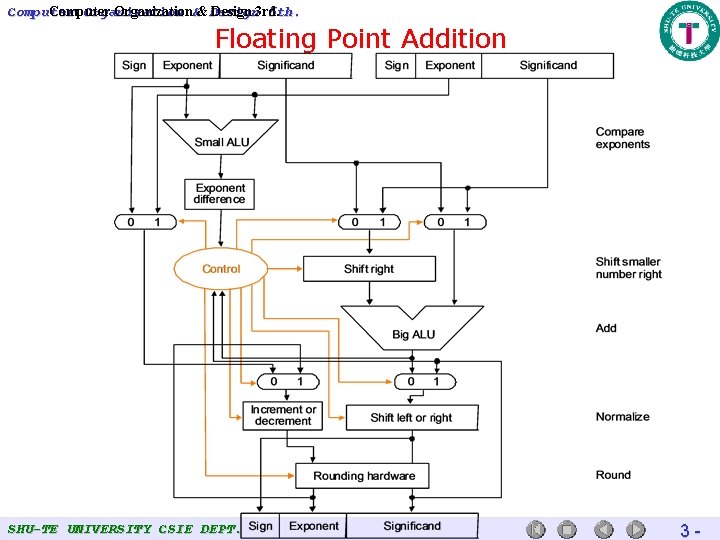
Computer Organization 5 th. Computer Organization&& Design 3 rd. Floating Point Addition • Decimal example: 9. 999 x 101 + 1. 610 x 10 -1 – Assume 4 decimal digits of significand (有效數字) and two of exponent • Algorithm – – Step 1: Align the decimal point (of the number of the smaller exponent) Step 2: Add significands Step 3: Convert to normalized form, check for underflow or overflow Step 4: Round the resulting significand SHU-TE UNIVERSITY CSIE DEPT. 3 -

Computer Organization 5 th. Computer Organization&& Design 3 rd. Floating Point Addition [Ex] 0. 5(10) + (-0. 4375)(10) [ANS] 0. 5 = 1. 000 × 2 -1 -0. 4375 = -1. 110 × 2 -2 Step 1: align the smaller number -1. 110 × 2 -2 = -0. 110 × 2 -1 Step 2: add the significands 1. 000 × 2 -1 + (-0. 110 × 2 -1) = 0. 001 × 2 -1 Step 3. normalize the sum, check O/U? (1) 0. 001 × 2 -1 = 1. 000 × 2 -4 (2) 127 -4 -126 No O/U Step 4: round the sum 1. 000 × 2 -4 = 0. 000100002 = 0. 062510 SHU-TE UNIVERSITY CSIE DEPT. 3 -

Computer Organization 5 th. Computer Organization&& Design 3 rd. Floating Point Addition SHU-TE UNIVERSITY CSIE DEPT. 3 -

Computer Organization 5 th. Computer Organization&& Design 3 rd. Floating Point Multiplication • Algorithm – Step 1: Add the exponent (then -127 since bias is counted twice) – Step 2: Multiply the two significands – Step 3: Normalized the result, check for underflow or overflow – Step 4: Round the resulting significand – Step 5: Determine the sign SHU-TE UNIVERSITY CSIE DEPT. 3 -

Computer Organization 5 th. Computer Organization&& Design 3 rd. Floating Point Multiplication [Ex] 0. 5(10) × (-0. 4375)(10) [ANS] 0. 5 = 1. 000 × 2 -1 -0. 4375 = -1. 110 × 2 -2 Step 1: add the exponents (-1) + (-2) = -3 E = -3 +127 = 124 = Step 2: multiply the significands 1. 000 × 1. 110 = 1. 110000 × 2 -3 Step 3. normalize the product, check O/U? (1) 1. 110 × 2 -3 (2) 127 -3 -126 No O/U Step 4: round the product 1. 110 × 2 -3 Step 5: check the signs of operands different -1. 110 × 2 -3 = -0. 00111 = -0. 21875 SHU-TE UNIVERSITY CSIE DEPT. 3 -

Computer Organization 5 th. Computer Organization&& Design 3 rd. Floating Point Rounding(捨位) • 計算浮點運算，其結果通常不等於真實結果。例如，0. 1001 × 0. 1101 = 0. 01110101。但是當精確度只有5位時，則結果將為 0. 01110或 0. 01111。該如何選擇即為「捨位法」 • Round to nearest – 如上例，若選 0. 01110，則誤差為 0. 000000101 – 若選 0. 01111，則誤差為 0. 00000011 • 若誤差相同時 – Choose the ‘even’ result. (IEEE standard!!) • Round to nearest or even!! SHU-TE UNIVERSITY CSIE DEPT. 3 -

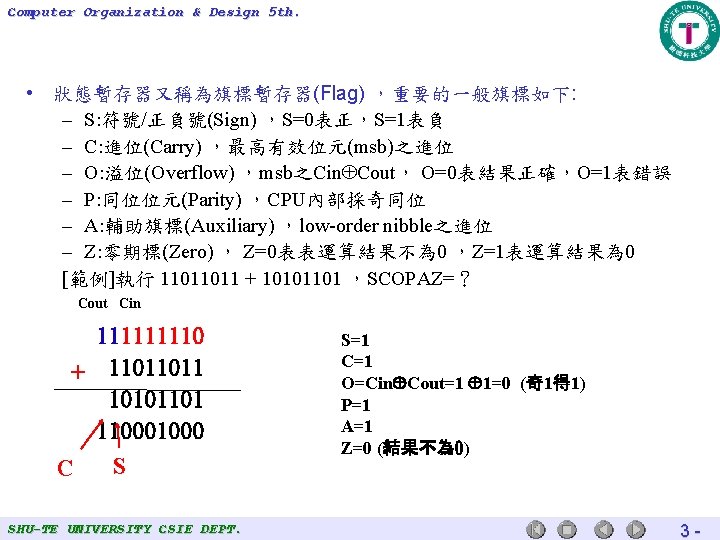
Computer Organization & Design 5 th. • 狀態暫存器又稱為旗標暫存器(Flag) ，重要的一般旗標如下: – S: 符號/正負號(Sign) ，S=0表正，S=1表負 – C: 進位(Carry) ，最高有效位元(msb)之進位 – O: 溢位(Overflow) ，msb之Cin Cout， O=0表結果正確，O=1表錯誤 – P: 同位位元(Parity) ，CPU內部採奇同位 – A: 輔助旗標(Auxiliary) ，low-order nibble之進位 – Z: 零期標(Zero) ， Z=0表表運算結果不為 0 ，Z=1表運算結果為 0 [範例]執行 11011011 + 10101101 ，SCOPAZ=？ Cout Cin 11110 11011011 10101101 11000 S C SHU-TE UNIVERSITY CSIE DEPT. S=1 C=1 O=Cin Cout=1 1=0 (奇1得 1) P=1 A=1 Z=0 (結果不為 0) 3 -