Computer Organization and Architecture Chapter 8 Computer Arithmetic

Computer Organization and Architecture Chapter 8 Computer Arithmetic 1

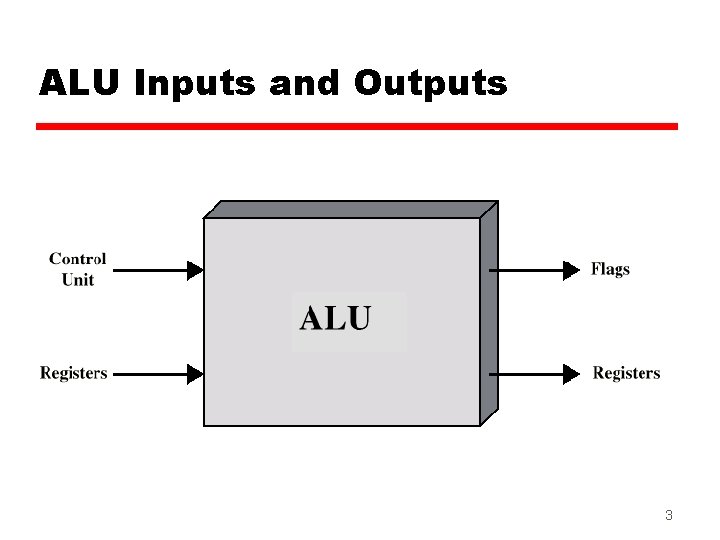
Arithmetic & Logic Unit z Does the calculations z Everything else in the computer is there to service this unit z Handles integers z May handle floating point (real) numbers z May be separate FPU (maths co-processor) z May be on chip separate FPU (486 DX +) 2

ALU Inputs and Outputs 3

Integer Representation z Only have 0 & 1 to represent everything z Positive numbers stored in binary ye. g. 41=00101001 z No minus sign z No period z Sign-Magnitude z Two’s compliment 4

Sign-Magnitude z Left most bit is sign bit z 0 means positive z 1 means negative z +18 = 00010010 z -18 = 10010010 z Problems y. Need to consider both sign and magnitude in arithmetic y. Two representations of zero (+0 and -0) 5

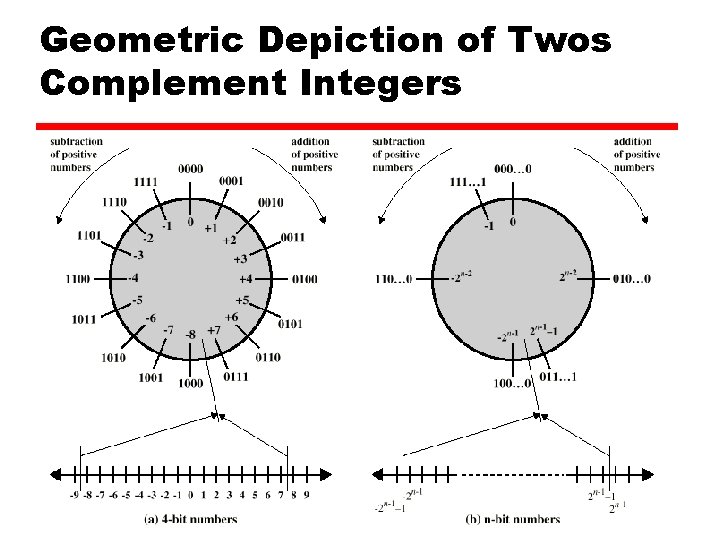
Two’s Compliment z +3 = 00000011 z +2 = 00000010 z +1 = 00000001 z +0 = 0000 z -1 = 1111 z -2 = 11111110 z -3 = 11111101 6

Benefits z One representation of zero z Arithmetic works easily (see later) z Negating is fairly easy y 3 = 00000011 y. Boolean complement gives 11111100 y. Add 1 to LSB 11111101 7

Geometric Depiction of Twos Complement Integers 8

Negation Special Case 1 z 0= 0000 z Bitwise not 1111 z Add 1 to LSB +1 z Result 1 0000 z Overflow is ignored, so: z- 0 = 0 9

Negation Special Case 2 z -128 = 10000000 z bitwise not 01111111 z Add 1 to LSB +1 z Result 10000000 z So: z -(-128) = -128 X z Monitor MSB (sign bit) z It should change during negation 10

Range of Numbers z 8 bit 2 s compliment y+127 = 01111111 = 27 -1 y -128 = 10000000 = -27 z 16 bit 2 s compliment y+32767 = 011111111 = 215 - 1 y -32768 = 100000000 = -215 11

Conversion Between Lengths z Positive number pack with leading zeros z +18 = 00010010 z +18 = 0000 00010010 z Negative numbers pack with leading ones z -18 = 10010010 z -18 = 1111 10010010 z i. e. pack with MSB (sign bit) 12

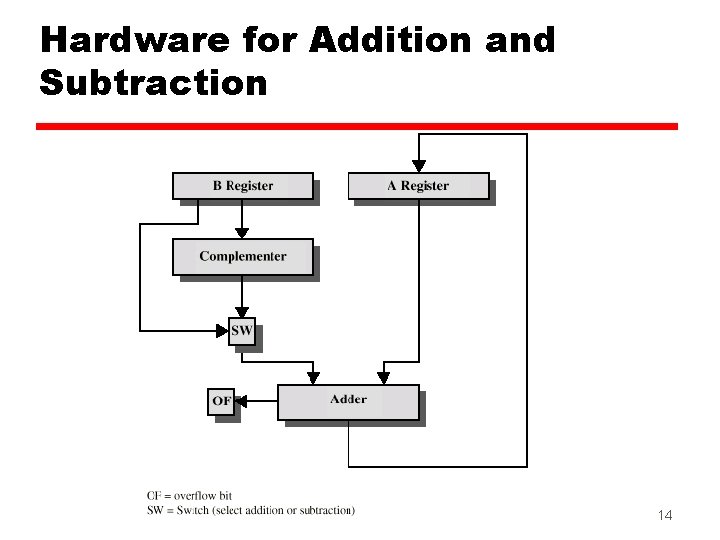
Addition and Subtraction z Normal binary addition z Monitor sign bit for overflow z Take twos compliment of substahend add to minuend yi. e. a - b = a + (-b) z So we only need addition and complement circuits 13

Hardware for Addition and Subtraction 14

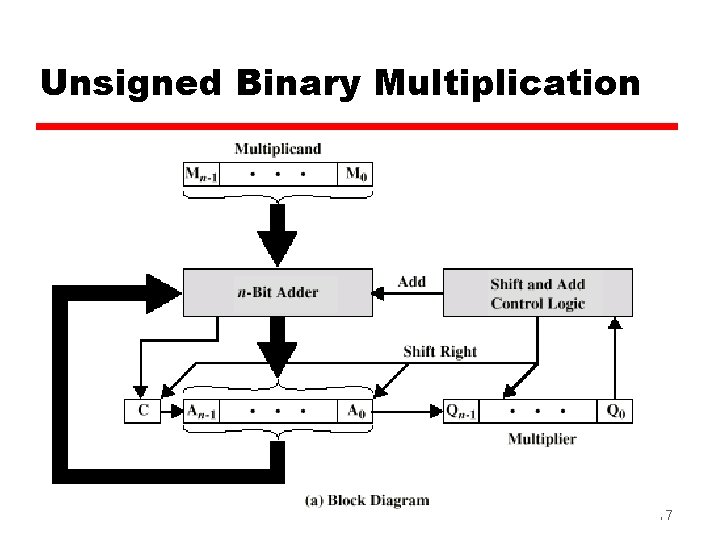
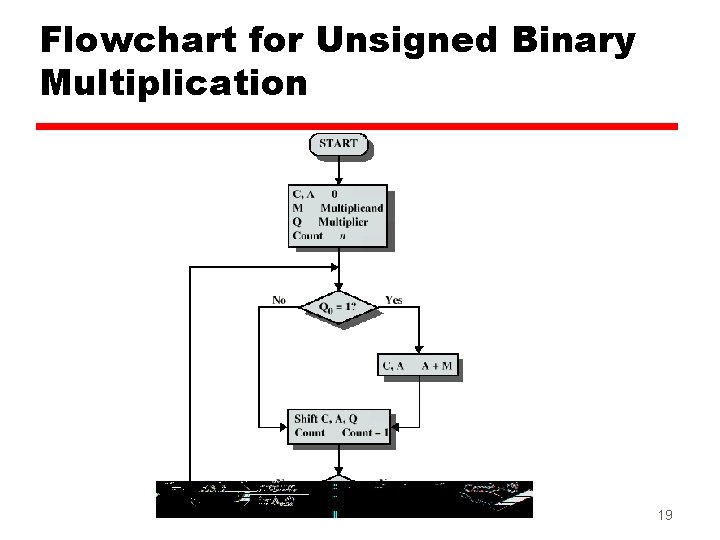
Multiplication z Complex z Work out partial product for each digit z Take care with place value (column) z Add partial products 15

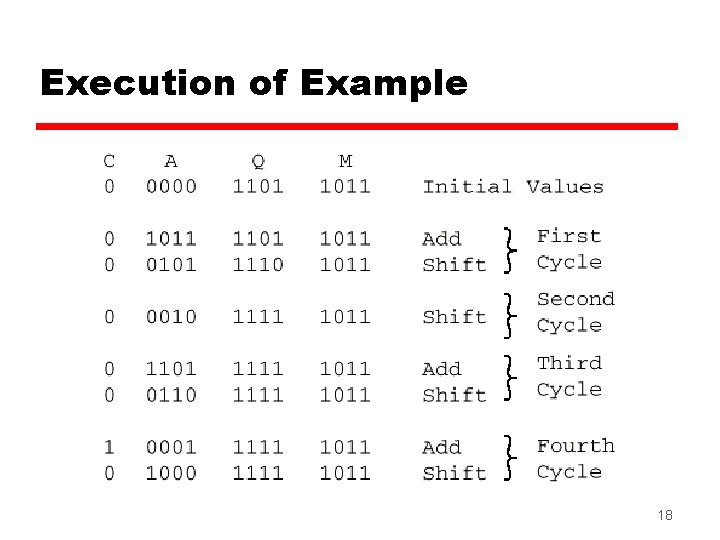
Multiplication Example z 1011 z 1101 z 1011 z 0000 z 1011 z 10001111 z Note: need Multiplicand (11 dec) Multiplier (13 dec) Partial products Note: if multiplier bit is 1 copy multiplicand (place value) otherwise zero Product (143 dec) double length result 16

Unsigned Binary Multiplication 17

Execution of Example 18

Flowchart for Unsigned Binary Multiplication 19

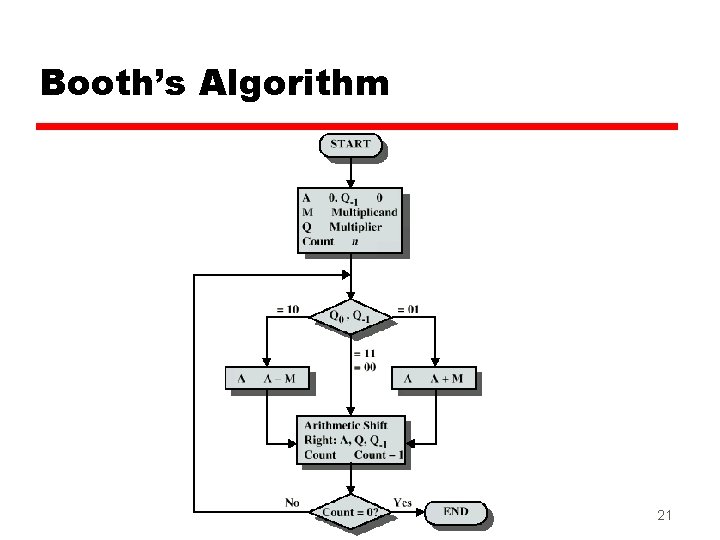
Multiplying Negative Numbers z This does not work! z Solution 1 y. Convert to positive if required y. Multiply as above y. If signs were different, negate answer z Solution 2 y. Booth’s algorithm 20

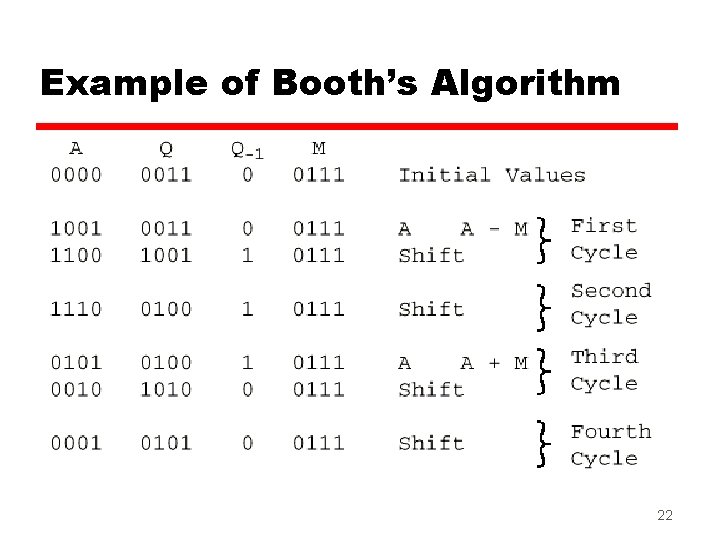
Booth’s Algorithm 21

Example of Booth’s Algorithm 22

Division z More complex than multiplication z Negative numbers are really bad! z Based on long division 23

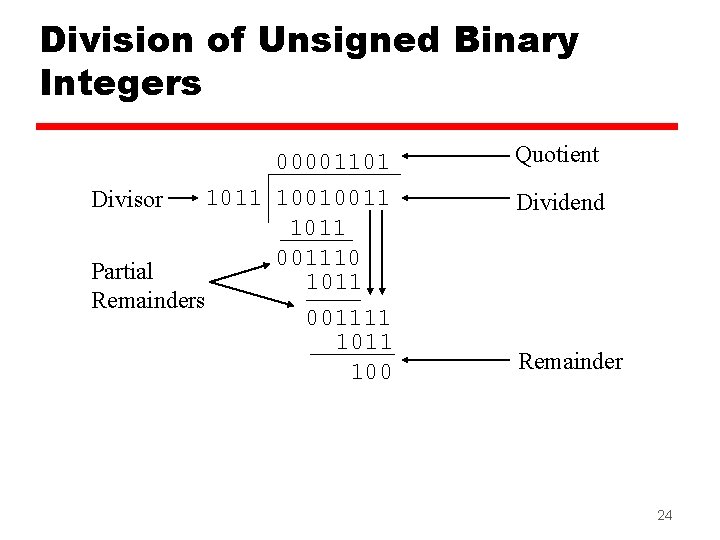
Division of Unsigned Binary Integers 00001101 1011 10010011 Divisor 1011 001110 Partial 1011 Remainders 001111 100 Quotient Dividend Remainder 24

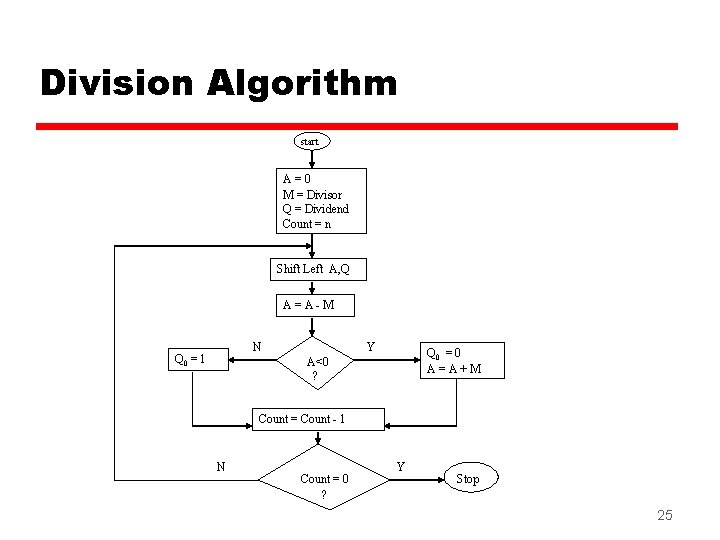
Division Algorithm start A=0 M = Divisor Q = Dividend Count = n Shift Left A, Q A=A-M N Q 0 = 1 Y Q 0 = 0 A=A+M A<0 ? Count = Count - 1 N Count = 0 ? Y Stop 25

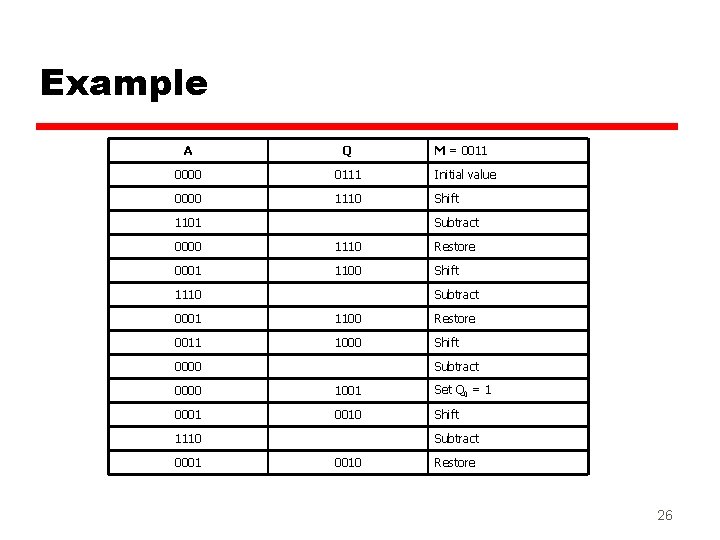
Example A Q 0000 0111 Initial value 0000 1110 Shift 1101 M = 0011 Subtract 0000 1110 Restore 0001 1100 Shift 1110 Subtract 0001 1100 Restore 0011 1000 Shift 0000 Subtract 0000 1001 Set Q 0 = 1 0001 0010 Shift 1110 0001 Subtract 0010 Restore 26

Real Numbers z Numbers with fractions z Could be done in pure binary y 1001. 1010 = 24 + 20 +2 -1 + 2 -3 =9. 625 z Where is the binary point? z Fixed? y. Very limited z Moving? y. How do you show where it is? 27

Sign bit Floating Point Biased Exponent Significand or Mantissa z +/-. significand x 2 exponent z Misnomer z Point is actually fixed between sign bit and body of mantissa z Exponent indicates place value (point position) 28

Floating Point Examples 29

Signs for Floating Point z Mantissa is stored in 2 s compliment z Exponent is in excess or biased notation ye. g. Excess (bias) 128 means y 8 bit exponent field y. Pure value range 0 -255 y. Subtract 128 to get correct value y. Range -128 to +127 30

Normalization z FP numbers are usually normalized z i. e. exponent is adjusted so that leading bit (MSB) of mantissa is 1 z Since it is always 1 there is no need to store it z (c. f. Scientific notation where numbers are normalized to give a single digit before the decimal point z e. g. 3. 123 x 103) 31

FP Ranges z For a 32 bit number y 8 bit exponent y+/- 2256 1. 5 x 1077 z Accuracy y. The effect of changing lsb of mantissa y 23 bit mantissa 2 -23 1. 2 x 10 -7 y. About 6 decimal places 32

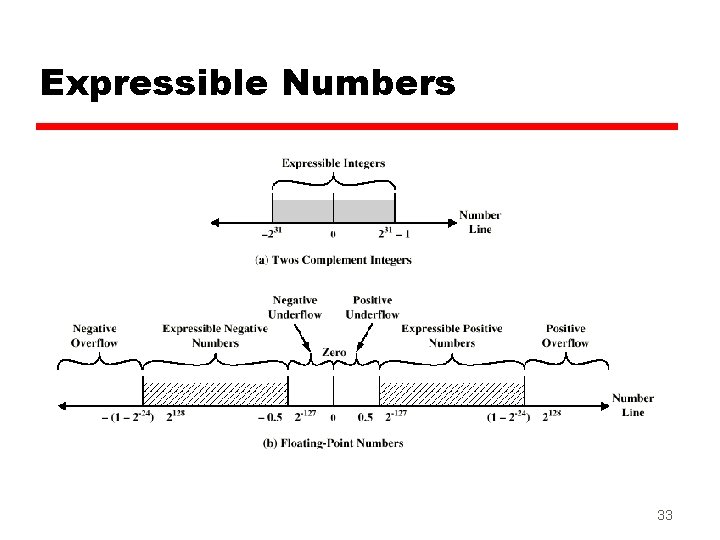
Expressible Numbers 33

IEEE 754 z Standard for floating point storage z 32 and 64 bit standards z 8 and 11 bit exponent respectively z Extended formats (both mantissa and exponent) for intermediate results 34

FP Arithmetic +/z Check for zeros z Align significands (adjusting exponents) z Add or subtract significands z Normalize result 35

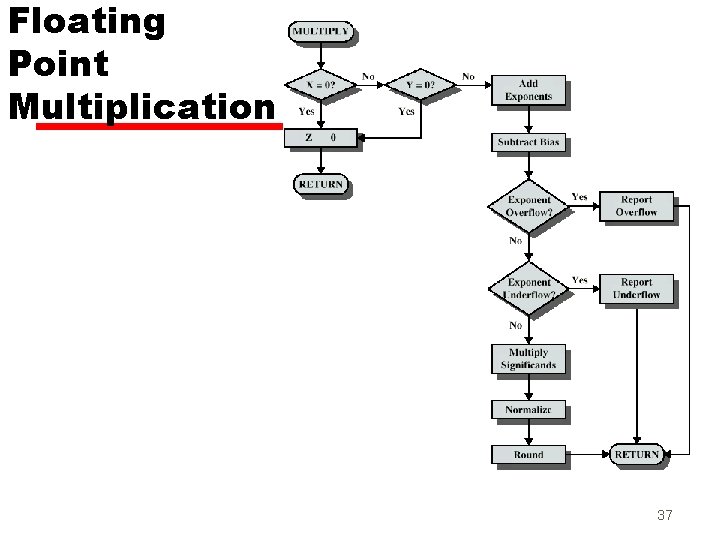
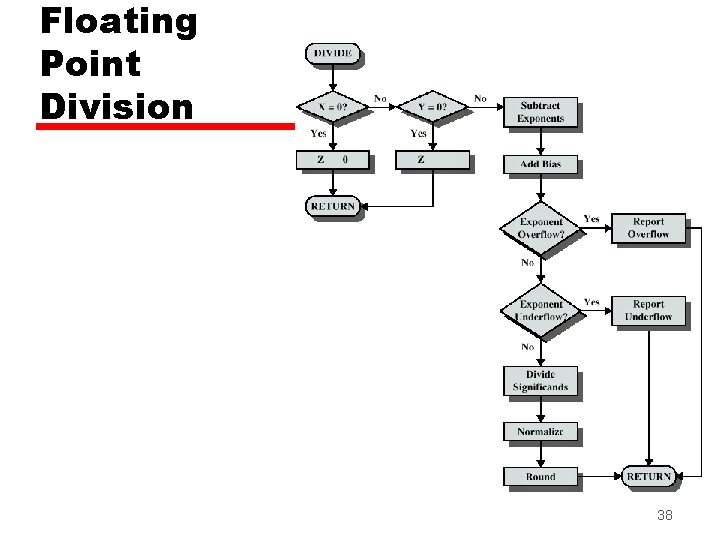
FP Arithmetic x/ z Check for zero z Add/subtract exponents z Multiply/divide significands (watch sign) z Normalize z Round z All intermediate results should be in double length storage 36

Floating Point Multiplication 37

Floating Point Division 38

Required Reading z Stallings Chapter 8 z IEEE 754 on IEEE Web site 39