Computer Number Systems Thorne Edition 2 Section 1

Computer Number Systems Thorne, Edition 2 : Section 1. 3, Appendix I (Irvine, Edition VI : Section 1. 3) SYSC 3006 1

Starting from What We Already Know … Decimal Numbers Based Number Systems : 1. Base defines set of symbols 2. Number = string of symbols 3. Interpretation rules – Digits numbered right to left, start at 0 eg. 4 -digit number d 3 d 2 d 1 d 0 – Value of digit depends on symbol and position within number – Value of number is sum of value of digits Decimal Numbers : Base-10 with symbols = { 0, 1, 2, 3, , 9} 4 -digit example: d 3 d 2 d 1 d 0 = 1436 = d 3 103 + d 2 102 + d 1 101 + d 0 100 = 1 103 + 4 102 + 3 101 + 6 100 Note : 1. Addition/Subtraction : We carry and borrow 10’s 2. Multiplication/Division by 10 : Shift right/left SYSC 3006 2

Applying Same Methods to Binary Numbers : Base-2 with symbols = { 0, 1} 4 -digit example: d 3 d 2 d 1 d 0 = 1010 b = d 3 23 + d 2 22 + d 1 21 + d 0 20 = 1 23 + 0 22 + 1 21 + 0 20 = 1 8 +0 4 +1 2 +0 1 =8+2 = 10 d Note : 1. Addition/Subtraction : We carry and borrow 2’s 2. Multiplication/Division by 2 : Shift right/left SYSC 3006 3

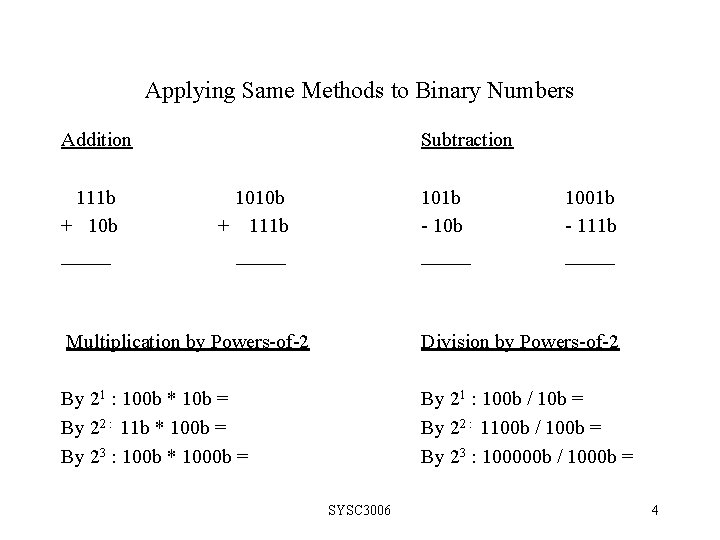
Applying Same Methods to Binary Numbers Addition 111 b + 10 b _____ Subtraction 1010 b + 111 b _____ 101 b - 10 b _____ 1001 b - 111 b _____ Multiplication by Powers-of-2 Division by Powers-of-2 By 21 : 100 b * 10 b = By 22 : 11 b * 100 b = By 23 : 100 b * 1000 b = By 21 : 100 b / 10 b = By 22 : 1100 b / 100 b = By 23 : 100000 b / 1000 b = SYSC 3006 4

4 -bit Binary Numbers you should know Binary Decimal 0000 0001 0010 0011 0100 0101 0110 0111 0 1 2 3 4 5 6 7 Binary Decimal 1000 1001 1010 1011 1100 1101 1110 1111 8 9 10 11 12 13 14 15 SYSC 3006 5

Range of Representation Within a computer, all numbers are represented in a finite-width – Registers are finite width, depending on processor – Memory cells are 8 or 16 or 32 or 64 -width Range : n-bit values can represent (at most) 2 n different counting numbers · If start representation at 0, then largest value represented is 2 n – 1 · Previous page : 4 -bit numbers Maximum number of values : 24 = 16 Range : 0. . 15 (24 – 1) Observation : Binary representation often requires lots of bits Example: 60110 = 10010110012 (10 bits!) Converting binary decimal is not so convenient SYSC 3006 6

Hexadecimal Numbers : Base 16 Why Base-16 ? 16 = 24 – Will provide us with a shortcut for working with large binary number analogous to acronyms (eg. CU, UBC, MIT) Hexadecimal Numbers : Base-16 with symbols = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F} 4 -digit example: d 3 d 2 d 1 d 0 = 12 AFh = d 3 163 + d 2 162 + d 1 161 + d 0 160 = 1 163 + 2 162 + A 161 + F 160 = 1 4096 + 2 256 + 10 16 + 15 1 = 4096 + 512 + 160 + 15 = 4783 d Addition/Subtraction : We carry and borrow 16’s · Multiplication/Division by 16 : Shift right/left SYSC 3006 7

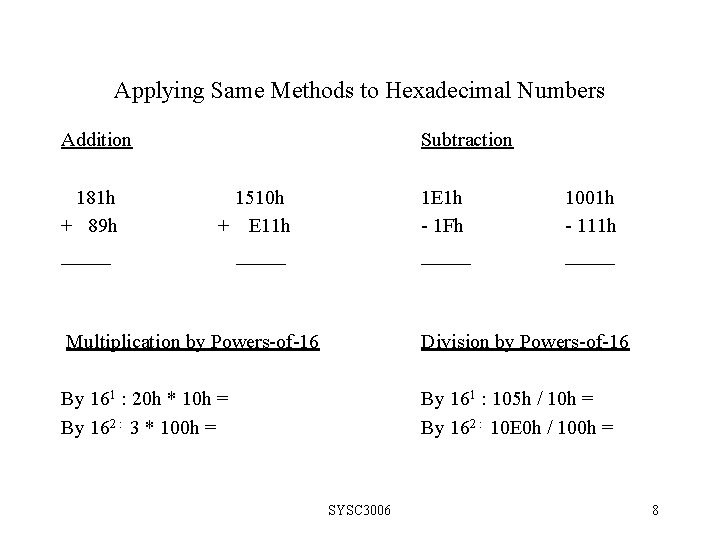
Applying Same Methods to Hexadecimal Numbers Addition 181 h + 89 h _____ Subtraction 1510 h + E 11 h _____ 1 E 1 h - 1 Fh _____ 1001 h - 111 h _____ Multiplication by Powers-of-16 Division by Powers-of-16 By 161 : 20 h * 10 h = By 162 : 3 * 100 h = By 161 : 105 h / 10 h = By 162 : 10 E 0 h / 100 h = SYSC 3006 8

Hexadecimal and Binary Numbers : 24 = 16 Converting Binary to Hexadecimal 16 -bit: 10001010011011102 (= 35, 43810) group in 4’s 1000 1010 0110 1110 replace with hex 8 A 6 E 16 10 -bit: 10010110012 (= 60110) group in 4’s 0010 0101 1001 replace with hex 2 5 9 16 Converting Hex Binary : Replace each hex digit by 4 -digit binary rep. Example : 134 h = 0001 0011 0100 b SYSC 3006 9

Common Pitfalls for Beginners 1. What do I mean when I say “ Ten hex” ? 2. Are these two the same thing ? 1010 0010 b and A 2 h 3. What are the widths of the following numbers ? 1001 0010 b 22 h 2 h 1010 b 4. Memory is always composed of bytes One byte = 8 bits Contents of a byte = 8 binary digits 0000 b … 1111 b = 2 hex digits = (2*4 bits) 00 h … FFh = 0 … 255 d SYSC 3006 10

Representing Negative Numbers For unsigned numbers (counting, whole) : – All n bits are used for the magnitude of the number – Example : 4 -bit number : 0000 b …. 1111 b For signed numbers (negative) : – One bit must be used for the sign : • Most significant bit = sign bit 0 = positive, 1 = negative – n-1 bits are used for the magnitude of the number. Encoding the magnitude portion : 2 typical approaches 1. Signed magnitude encoding : • A natural progression from unsigned numbers, but … • No good for math 2. Two’s complement encoding • Hard to understand, but • Math works SYSC 3006 11

Signed Magnitude Encoding of Signed Numbers Magnitude encoded in remaining n – 1 bits using binary number system (as for counting #s) Example : 10000001 b = -1 d magnitude = 0001 b = 1 sign bit = 1 negative number Problems 1. Two representations for 0 positive 0 (sign bit = 0) negative 0 (sign bit = 1) 2. Awkward arithmetic operations 0000 0010 b 2 + 1000 0001 b + -1 1000 0011 -3 SYSC 3006 12

Two’s Complement Encoding of Signed Numbers Magnitude of negative numbers encoded with “flip-and-add” Magnitude of positive numbers encoded as “normal” binary number Definitions : complement of one bit: b = 1 – b complement of 0 = 1 complement of 1 = 0 · 1 s’ complement of an n-bit value: complement each bit · 2’s complement of an n-bit value: complement each bit, and then add 1 (flip-and-add) · Ignore any carry out of most significant bit SYSC 3006 13

Two’s Complement Encoding of Signed Numbers Example : Find the 8 -bit 2’s complement representation of – 1. +110 0001 b 2’s complement Complement 1111 1110 b operation Add 1 + 1 – 110 1111 b = FFh Encoding of negative numbers is “weird” ! Example : Find the 8 -bit 2’s complement representation of +1. +110 0001 b = 01 h That’s it! SYSC 3006 14

Two’s Complement Encoding of Signed Numbers Example : Find the decimal value of this 2’s complement number FEh (sign bit = 1) 1111 1110 b 2’s complement Complement 0000 0001 b operation Add 1 + 1 0000 0010 b = 2 d FEh = -2 d Example : Find the decimal value of this 2’s complement number 79 h (sign bit = 0) 0111 1001 b = 64 + 32 + 16 + 8 + 1 = 121 d SYSC 3006 15

Range of Signed Representations Whether using signed magnitude or 2’s complement MSBit = sign bit magnitude = n-1 remaining bits Range : n-bit values still represent (at most) 2 n different counting numbers, but… · Use half of binary values for negative values (i. e. 2 n– 1 values) , the rest for positive (and 0) Range for negative and positive values : All negatives start with 1. -2 n – 1 …. 0 …. 2 n – 1 -1 (Total 2 n numbers) SYSC 3006 16

Why 2’Complement for Signed Numbers ? 1. Negating a negated number should give the original number – (– x) = x – 110 complement add 1 +110 1111 0000 + 1 0000 0001 2. How many representations for 0? 010 0000 complement 1111 add 1 + 1 010 0000 SYSC 3006 It works ! ignore carry out of most significant bit 17

One Special Case with 2’Complement for Signed Numbers Consider 8 -bit 2’s complement encodings: · 28 = 256, 27 = 128 · range: – 128. . + 127 (– 2 n – 1) (2 n – 1) +12710 complement add 1 – 12710 0111 1000 0000 + 1 1000 0001 SYSC 3006 18

One Special Case with 2’Complement for Signed Numbers How to get encoding for – 128 ? 1. Using math – 127 – 1 = – 128 – 12710 subtract 1 – 12810 – 1000 0001 1 1000 0000 2. Using 2’s complement What if we negate – 128 ? [ special case !! ] – 12810 1000 0000 complement 0111 1111 add 1 + 1 – 12810 1000 0000 SYSC 3006 19

Character Encoding Representation of “displayable” characters: · characters: { A, B , . . . , Y, Z } · 26 2 = 52 (upper and lower case) · decimal (10) digits: {0, 1, . . . , 8, 9 } · punctuation: ! , . – ? / : ; · math symbols: + * = ( – and / above) · brackets: ( ) [ ] { } < > · others: @ # $ % ^ & | ~ · blank space: “ ” · 90+ symbols (? ? ) Various encoding schemes have been used SYSC 3006 20

(7 -bit) ASCII character encoding ASCII = American Standard Code for Information Interchange 7 -Bit ASCII Encoding · 7 bits to encode each character (128 codes) · often extended to 8 -bit (byte) values by making most significant bit (msb) = 0 [in following: all codes are given as hex values] 00 – 1 F non-displayable control char’s · 00 h NULL · 07 h BELL · 08 h backspace · 09 h tab · 0 Ah line feed · 0 Ch form feed · 0 Dh carriage return · others – often serve special purposes in communication applications SYSC 3006 21

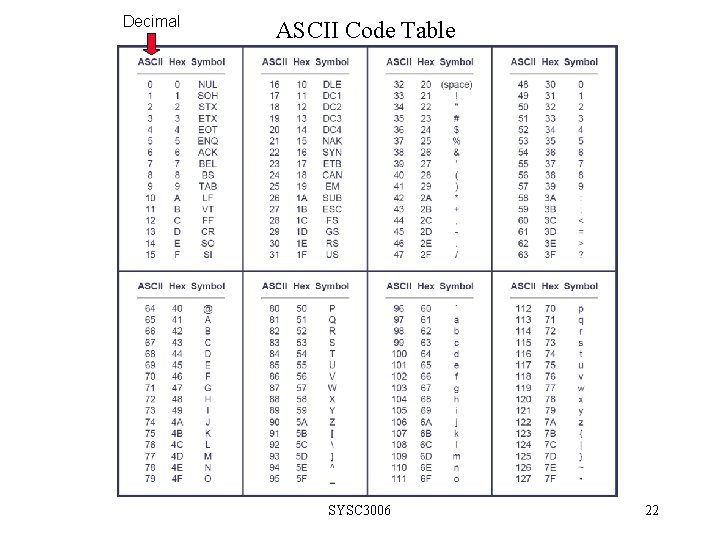
Decimal ASCII Code Table SYSC 3006 22

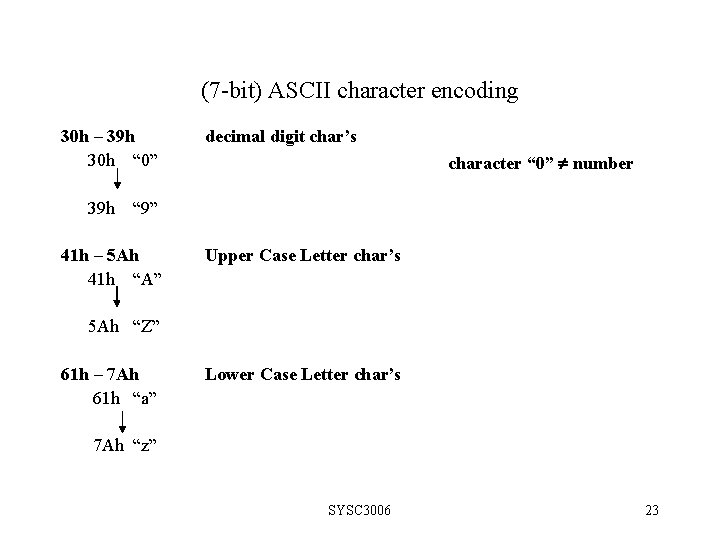
(7 -bit) ASCII character encoding 30 h – 39 h 30 h “ 0” 39 h decimal digit char’s character “ 0” number “ 9” 41 h – 5 Ah 41 h “A” Upper Case Letter char’s 5 Ah “Z” 61 h – 7 Ah 61 h “a” Lower Case Letter char’s 7 Ah “z” SYSC 3006 23

(7 -bit) ASCII character encoding · Example : encoding: shorthand for binary! “ 306 is FUN!” 33 30 36 20 69 73 20 46 55 4 E 21 00110000 01110011 Other Character Encoding Schemes: · IBM standardized an 8 -bit scheme (256 char’s) as defacto standard (PC’s !) · See Appendix I : overlaps with 7 -bit ASCII for displayable char’s · Java: unicode – 16 -bit scheme (65, 536 char’s) multi-lingual character sets SYSC 3006 24

Programmers : Be Aware Important Concept !!!!!! · fixed-width binary values are used to represent information in computers · the computer works with the binary representations (NOT the information!!) · the same binary value can be used to represent different information ! 8 -bit example: unsigned: 8 -bit ASCII: other? 1111 00002 24010 – 1610 “ ” SYSC 3006 25