Computer Number System Recommended For Pharmacy Student 13

Computer Number System Recommended For Pharmacy Student ! 13 Part Pharm-D (Doctor of Pharmacy), DPT (Doctor of Physiotherapy) & Pharmacy Technician. MUHAMMAD MUNIM AKHTAR Computer & its Applications in Pharmacy with Munim

Welcome to Computer & its Application in Pharmacy with Munim Akhtar Free online quality educational tutorials about Computer in Pharmacy Computer & its Applications in Pharmacy with Munim

Computer & its Applications in Pharmacy with Munim

NUMBER SYSTEMS Computer & its Applications in Pharmacy with Munim

INTRODUCTION • Number systems are simply ways to count things. • There is no symbol for “ 10” – or for the base of any system. We count 1, 2, 3, 4, 5, 6, 7, 8, 9, and then put a 0 in the first column and add a new left column, starting at 1 again. Then we count 1 -9 in the first column again. • A number can be represented differently in different systems. For example, • The numbers 2 A 16, 528, 4210. Computer & its Applications in Pharmacy with Munim

INTRODUCTION • We are all familiar with the decimal number system (Base 10). Some other number systems that called positional number system are: • Binary Base 2 • Octal Base 8 • Hexadecimal Base 16 Computer & its Applications in Pharmacy with Munim

THE DECIMAL SYSTEM Computer & its Applications in Pharmacy with Munim
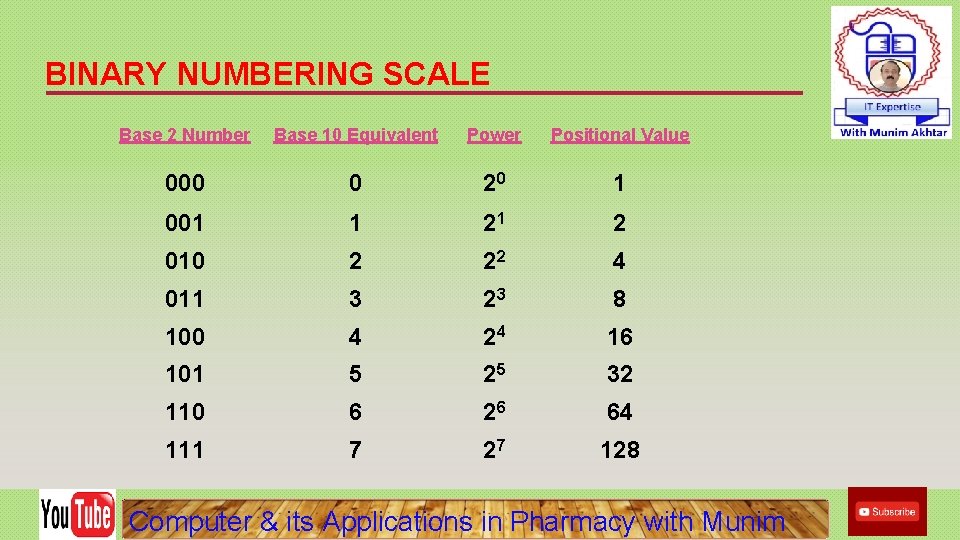
BINARY NUMBERING SCALE Base 2 Number Base 10 Equivalent Power Positional Value 000 0 20 1 001 1 21 2 010 2 22 4 011 3 23 8 100 4 24 16 101 5 25 32 110 6 26 64 111 7 27 128 Computer & its Applications in Pharmacy with Munim

BINARY NUMBER SYSTEM • Also called the “Base 2 system” • The binary number system is used to model the series of electrical signals computers use to represent information • 0 represents the no voltage or an off state • 1 represents the presence of voltage or an on state Computer & its Applications in Pharmacy with Munim

COMMON NUMBER SYSTEMS System Base Symbols Used by humans? Used in computers? Decimal 10 0, 1, … 9 Yes No Binary 2 0, 1 No Yes Octal 8 0, 1, … 7 No No Hexadecimal 16 0, 1, … 9, A, B, … F No No Computer & its Applications in Pharmacy with Munim

QUANTITIES/COUNTING (1 OF 3) Decimal Binary Octal Hexadecimal 0 0 1 1 2 10 2 2 3 11 3 3 4 100 4 4 5 101 5 5 6 110 6 6 7 111 7 7 Computer & its Applications in Pharmacy with Munim
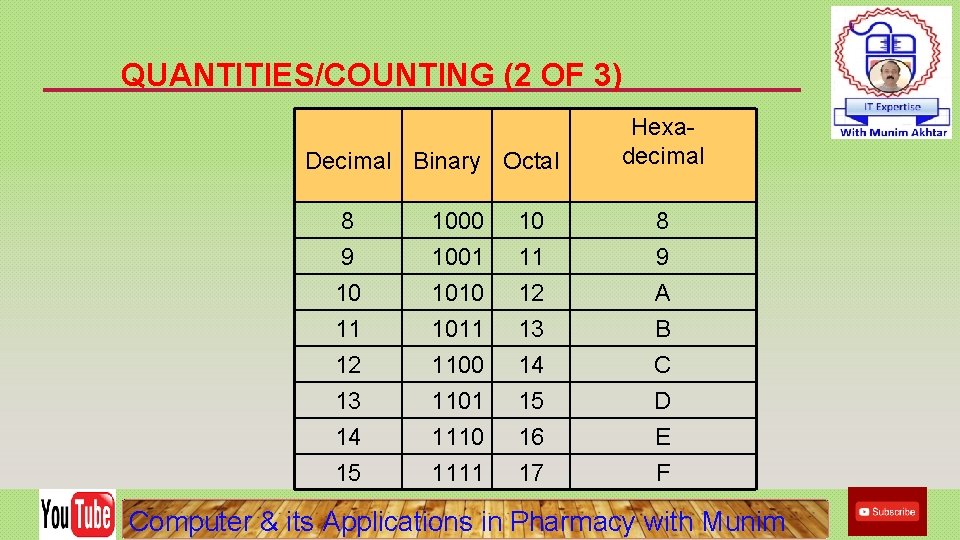
QUANTITIES/COUNTING (2 OF 3) Decimal Binary Octal Hexadecimal 8 1000 10 8 9 1001 11 9 10 1010 12 A 11 1011 13 B 12 1100 14 C 13 1101 15 D 14 1110 16 E 15 1111 17 F Computer & its Applications in Pharmacy with Munim
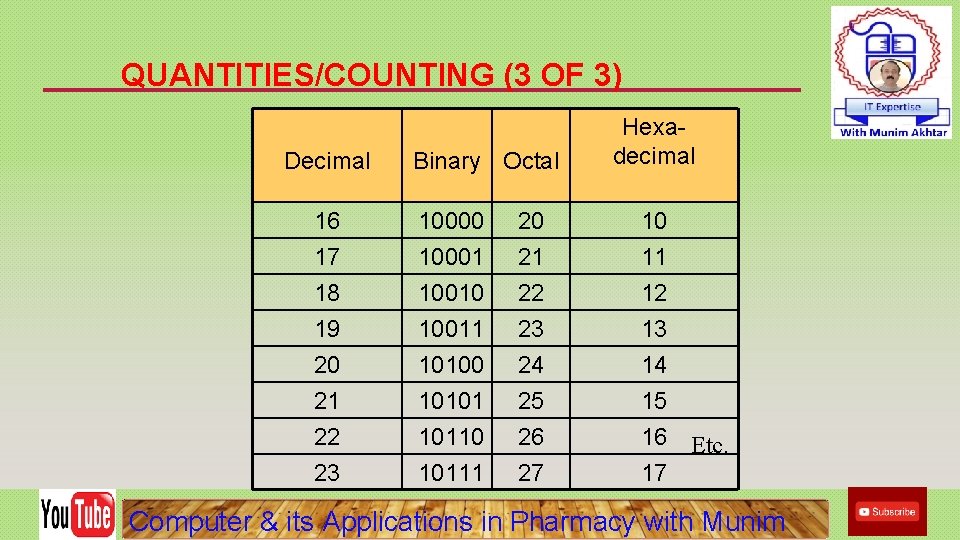
QUANTITIES/COUNTING (3 OF 3) Decimal Binary Octal Hexadecimal 16 10000 20 10 17 10001 21 11 18 10010 22 12 19 10011 23 13 20 10100 24 14 21 10101 25 15 22 10110 26 23 10111 27 16 Etc. 17 Computer & its Applications in Pharmacy with Munim

CONVERSION AMONG BASES • The possibilities: Decimal Octal Binary Hexadecimal Computer & its Applications in Pharmacy with Munim

DECIMAL TO BINARY CONVERSION • The easiest way to convert a decimal number to its binary equivalent is to use the Division method (Algorithm) • This method repeatedly divides a decimal number by 2 and records the quotient and remainder Computer & its Applications in Pharmacy with Munim

QUICK EXAMPLE Decimal no 2510 Binary no. =110012 Octal no =318 Hexadecimal no =1916 Base Computer & its Applications in Pharmacy with Munim

DECIMAL TO DECIMAL (JUST FOR FUN) Decimal Octal Binary Hexadecimal Next slide… Computer & its Applications in Pharmacy with Munim

Weight 12510 => 5 x 100 = 2 x 101 = 1 x 102 = Base 5 20 100 125 Computer & its Applications in Pharmacy with Munim
BINARY TO DECIMAL Decimal Octal Binary Hexadecimal Computer & its Applications in Pharmacy with Munim

BINARY TO DECIMAL CONVERSION • The easiest method for converting a binary number to its decimal equivalent is to use the Multiplication Algorithm • Multiply the binary digits by increasing powers of two, starting from the right • Then, to find the decimal number equivalent, sum those products Computer & its Applications in Pharmacy with Munim

SIGNIFICANT DIGITS Computer & its Applications in Pharmacy with Munim

BINARY TO DECIMAL • Technique • Multiply each bit by 2 n, where n is the “weight” of the bit • The weight is the position of the bit, starting from 0 on the right • Add the results Computer & its Applications in Pharmacy with Munim

EXAMPLE Bit “ 0” 1010112 => 1 1 0 1 x x x 20 21 22 23 24 25 = = = 1 2 0 8 0 32 4310 Computer & its Applications in Pharmacy with Munim
OCTAL TO DECIMAL Decimal Octal Binary Hexadecimal Computer & its Applications in Pharmacy with Munim

OCTAL NUMBER SYSTEM • Also known as the Base 8 System • Uses digits 0 - 7 • Readily converts to binary • Groups of three (binary) digits can be used to represent each octal digit • Also uses multiplication and division algorithms for conversion to and from base 10 Computer & its Applications in Pharmacy with Munim

OCTAL TO DECIMAL • Technique • Multiply each bit by 8 n, where n is the “weight” of the bit • The weight is the position of the bit, starting from 0 on the right • Add the results Computer & its Applications in Pharmacy with Munim

EXAMPLE Weight 7248 => Base 4 x 80 = 2 x 81 = 7 x 82 = 4 16 448 46810 Base Computer & its Applications in Pharmacy with Munim
HEXADECIMAL TO DECIMAL Decimal Octal Binary Hexadecimal Computer & its Applications in Pharmacy with Munim

HEXADECIMAL NUMBER SYSTEM • Base 16 system • Uses digits 0 -9 & letters A, B, C, D, E, F • Groups of four bits represent each base 16 digit Computer & its Applications in Pharmacy with Munim

HEXADECIMAL TO DECIMAL • Technique • Multiply each bit by 16 n, where n is the “weight” of the bit • The weight is the position of the bit, starting from 0 on the right • Add the results Computer & its Applications in Pharmacy with Munim
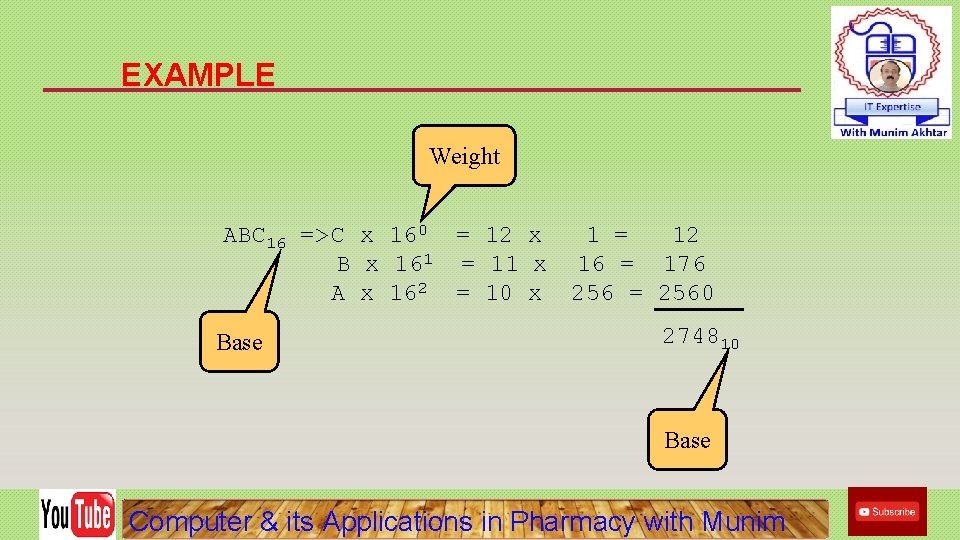
EXAMPLE Weight ABC 16 => C x 160 = 12 x 1 = 12 B x 161 = 11 x 16 = 176 A x 162 = 10 x 256 = 2560 Base 274810 Base Computer & its Applications in Pharmacy with Munim
DECIMAL TO BINARY Decimal Octal Binary Hexadecimal Computer & its Applications in Pharmacy with Munim

DECIMAL TO BINARY • Technique • Divide by two, keep track of the remainder • First remainder is bit 0 (LSB, least-significant bit) • Second remainder is bit 1 • Etc. Computer & its Applications in Pharmacy with Munim
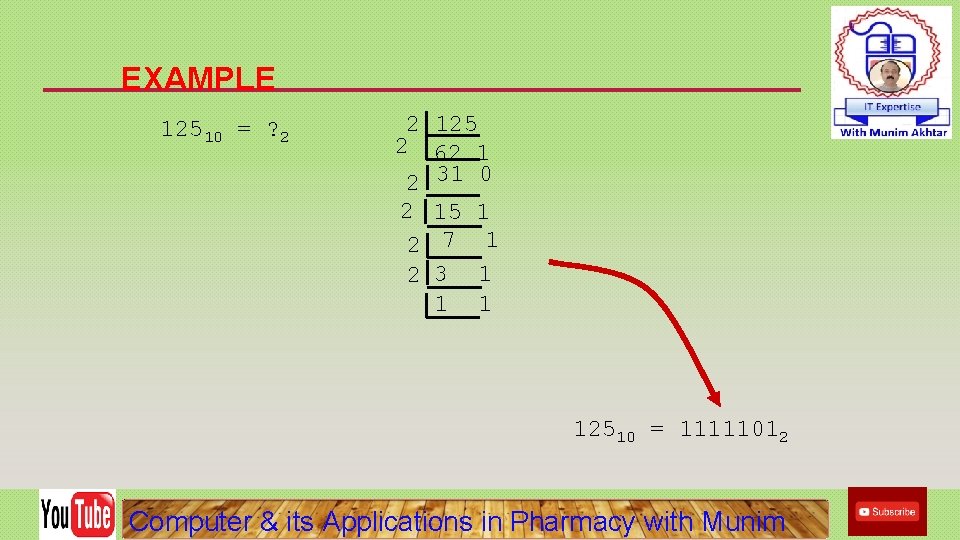
EXAMPLE 12510 = ? 2 2 125 2 62 1 2 31 0 2 15 1 2 7 1 2 3 1 12510 = 11111012 Computer & its Applications in Pharmacy with Munim
OCTAL TO BINARY Decimal Octal Binary Hexadecimal Computer & its Applications in Pharmacy with Munim

OCTAL TO BINARY • Technique • Convert each octal digit to a 3 -bit equivalent binary representation Computer & its Applications in Pharmacy with Munim

EXAMPLE 7058 = ? 2 7 0 5 111 000 101 7058 = 1110001012 Computer & its Applications in Pharmacy with Munim
HEXADECIMAL TO BINARY Decimal Octal Binary Hexadecimal Computer & its Applications in Pharmacy with Munim

HEXADECIMAL TO BINARY • Technique • Convert each hexadecimal digit to a 4 -bit equivalent binary representation Computer & its Applications in Pharmacy with Munim

EXAMPLE 10 AF 16 = ? 2 1 0 A F 0001 0000 1010 1111 10 AF 16 = 000101011112 Computer & its Applications in Pharmacy with Munim

DECIMAL TO OCTAL Decimal Octal Binary Hexadecimal Computer & its Applications in Pharmacy with Munim

DECIMAL TO OCTAL • Technique • Divide by 8 • Keep track of the remainder Computer & its Applications in Pharmacy with Munim
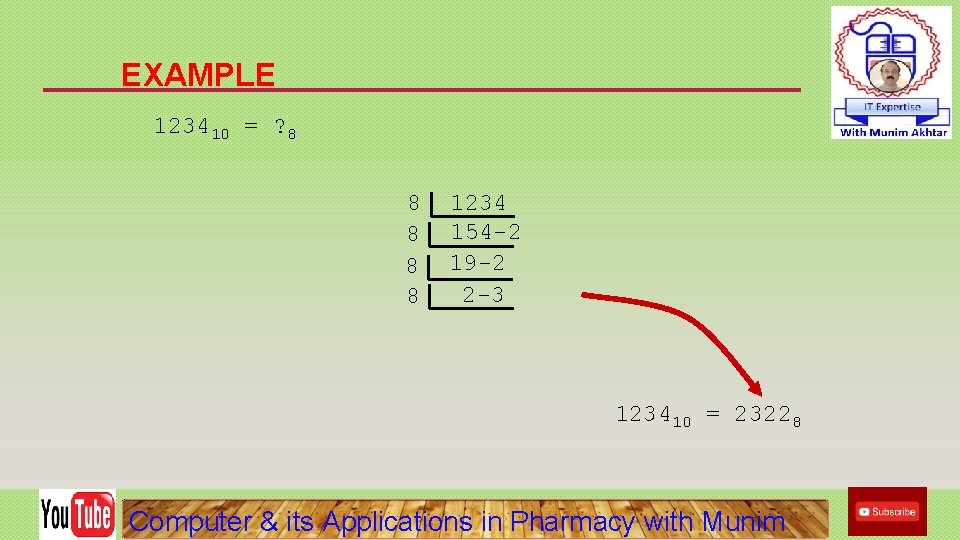
EXAMPLE 123410 = ? 8 8 8 1234 154 -2 19 -2 2 -3 123410 = 23228 Computer & its Applications in Pharmacy with Munim
DECIMAL TO HEXADECIMAL Decimal Octal Binary Hexadecimal Computer & its Applications in Pharmacy with Munim

DECIMAL TO HEXADECIMAL • Technique • Divide by 16 • Keep track of the remainder Computer & its Applications in Pharmacy with Munim
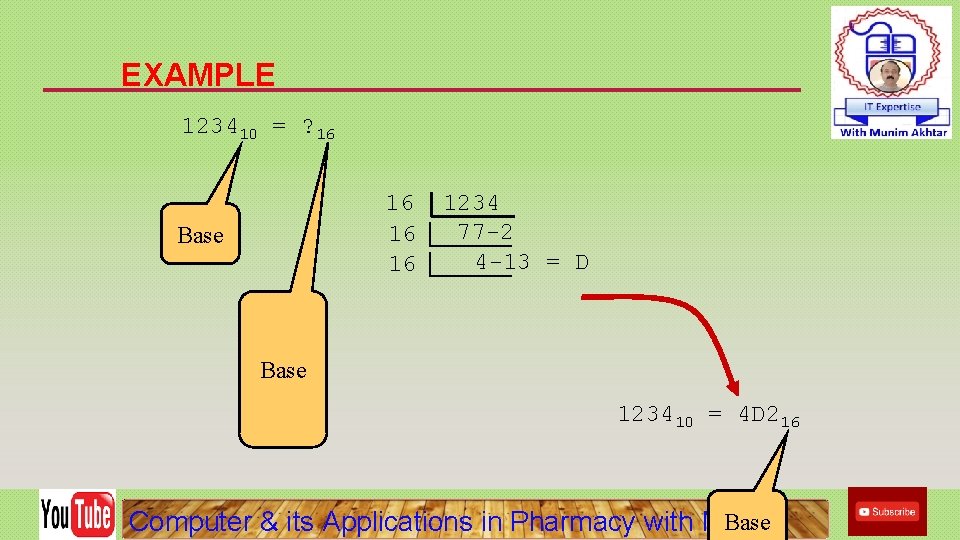
EXAMPLE 123410 = ? 16 16 Base 1234 77 -2 4 -13 = D Base 123410 = 4 D 216 Base Computer & its Applications in Pharmacy with Munim

BINARY TO OCTAL Decimal Octal Binary Hexadecimal Computer & its Applications in Pharmacy with Munim

BINARY TO OCTAL • Technique • Group bits in threes, starting on right • Convert to octal digits Computer & its Applications in Pharmacy with Munim
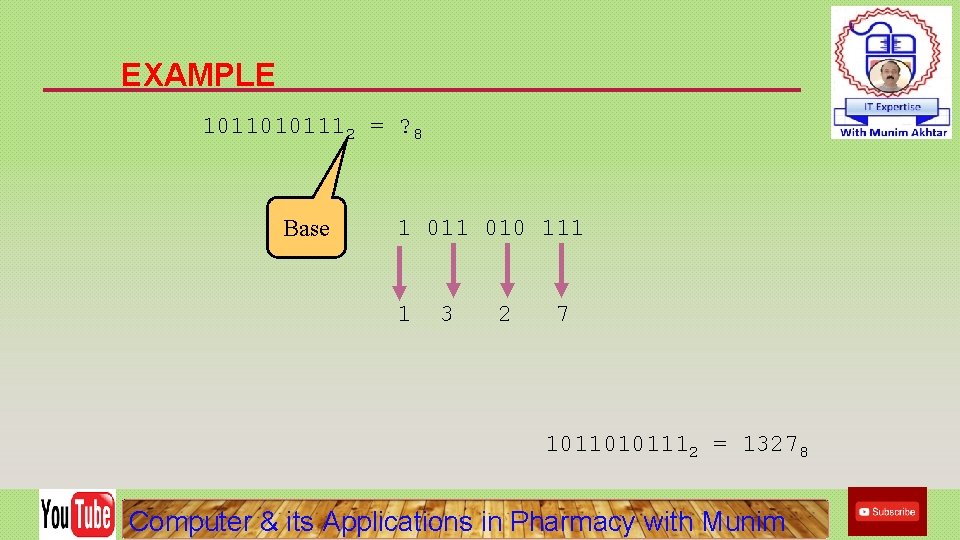
EXAMPLE 10110101112 = ? 8 Base 1 010 111 1 3 2 7 10110101112 = 13278 Computer & its Applications in Pharmacy with Munim
BINARY TO HEXADECIMAL Decimal Octal Binary Hexadecimal Computer & its Applications in Pharmacy with Munim

BINARY TO HEXADECIMAL • Technique • Group bits in fours, starting on right • Convert to hexadecimal digits Computer & its Applications in Pharmacy with Munim

MULTIPLICATION ALGORITHM Computer & its Applications in Pharmacy with Munim
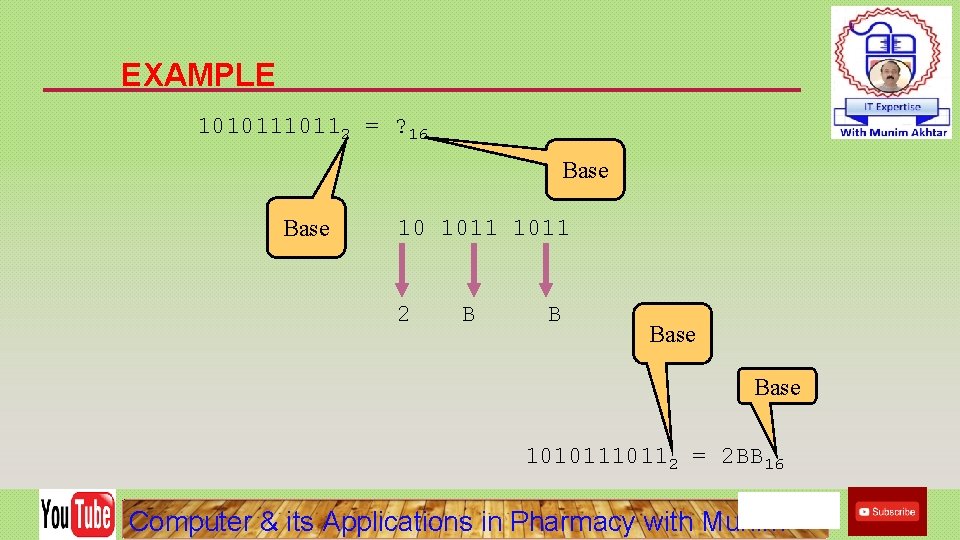
EXAMPLE 1010112 = ? 16 Base 10 1011 2 B B Base 1010112 = 2 BB 16 Computer & its Applications in Pharmacy with Munim

OCTAL TO HEXADECIMAL Decimal Octal Binary Hexadecimal Computer & its Applications in Pharmacy with Munim

OCTAL TO HEXADECIMAL • Technique • Use binary as an intermediary Computer & its Applications in Pharmacy with Munim

EXAMPLE 10768 = ? 16 1 0 7 6 001 000 111 110 Base 2 3 E Base 10768 = 23 E 16 Computer & its Applications in Pharmacy with Munim

HEXADECIMAL TO OCTAL Decimal Octal Binary Hexadecimal Computer & its Applications in Pharmacy with Munim

HEXADECIMAL TO OCTAL • Technique • Use binary as an intermediary Computer & its Applications in Pharmacy with Munim
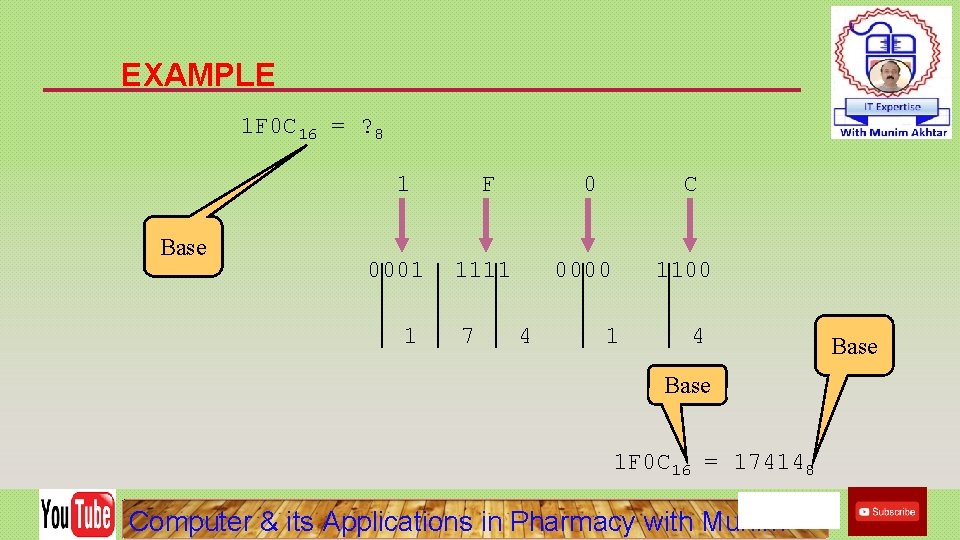
EXAMPLE 1 F 0 C 16 = ? 8 1 Base 0001 1 F 0 1111 7 C 0000 4 1100 1 4 Base 1 F 0 C 16 = 174148 Computer & its Applications in Pharmacy with Munim Base

EXERCISE – CONVERT. . . Decimal 33 Binary Octal Hexadecimal 1110101 703 1 AF Don’t use a calculator! Skip answer Answer Computer & its Applications in Pharmacy with Munim
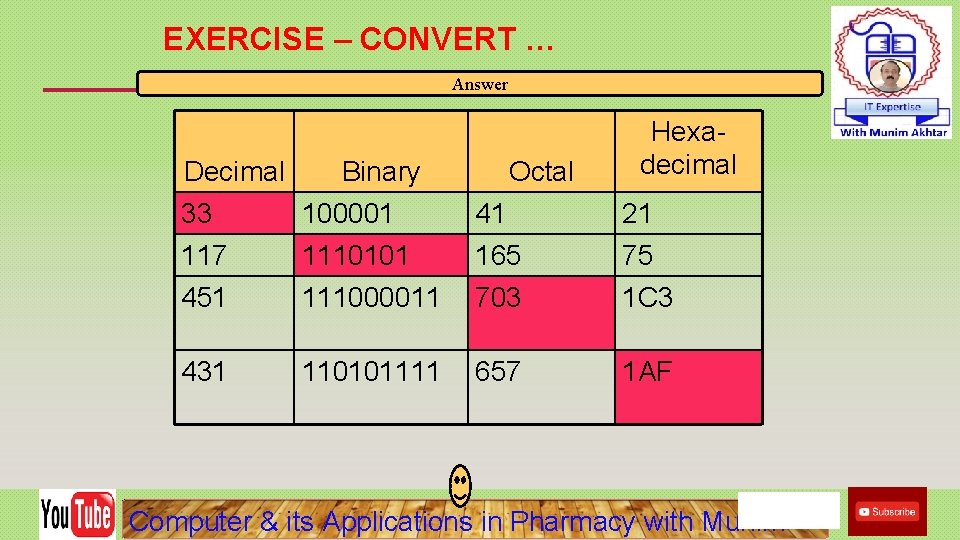
EXERCISE – CONVERT … Answer Decimal Binary 33 100001 117 1110101 451 111000011 41 165 703 21 75 1 C 3 431 657 1 AF 110101111 Octal Hexadecimal Computer & its Applications in Pharmacy with Munim
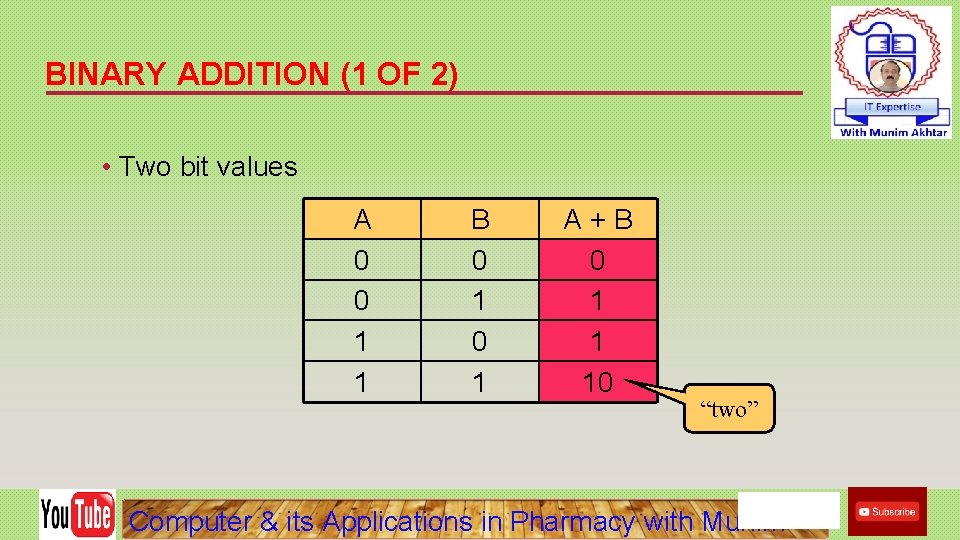
BINARY ADDITION (1 OF 2) • Two bit values A 0 0 1 1 B 0 1 A+B 0 1 1 10 “two” Computer & its Applications in Pharmacy with Munim

BINARY ADDITION (2 OF 2) • Two n-bit values • Add individual bits • Propagate carries • E. g. , 1 1 10101 101110 + 21 25 46 Computer & its Applications in Pharmacy with Munim

MULTIPLICATION (1 OF 3) • Decimal multiplication (just for fun) 35 x 105 175 00 x 35 xx 3675 Computer & its Applications in Pharmacy with Munim

BINARY MULTIPLICATION (2 OF 3) • Binary, multiplication two bit values A 0 0 1 1 B 0 1 A B 0 0 0 1 Computer & its Applications in Pharmacy with Munim

MULTIPLICATION (3 OF 3) • Binary, Multiplication two bit values • As with decimal values • E. g. , 1110 x 1011 1110 0000 1110 10011010 Computer & its Applications in Pharmacy with Munim

EXAMPLE OF MULTIPLICATION … Q = = = Ans. = Computer & its Applications in Pharmacy with Munim

? Computer & its Applications in Pharmacy with Munim

Computer & its Applications in Pharmacy with Munim
- Slides: 69