Computer Networks Lecture 21 Distance Vector Routing Protocols

Computer Networks Lecture 21 Distance Vector Routing Protocols 11/14/2013 1

Outline q Admin and recap q Distance vector protocols 2

Admin q Any questions on Assignment 4? 3

Recap: Resource Allocation Framework r Forward (design) engineering: m how to determine objective functions m given objective, how to design effective alg r Reverse (understand) engineering: m understand current protocols (what are the objectives of TCP/Reno, TCP/Vegas? ) 4

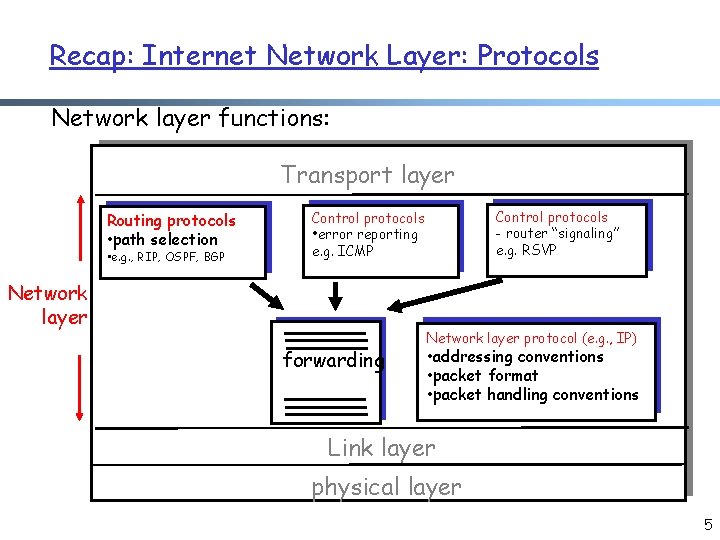
Recap: Internet Network Layer: Protocols Network layer functions: Transport layer Routing protocols • path selection • e. g. , RIP, OSPF, BGP Control protocols - router “signaling” e. g. RSVP Control protocols • error reporting e. g. ICMP Network layer forwarding Network layer protocol (e. g. , IP) • addressing conventions • packet format • packet handling conventions Link layer physical layer 5

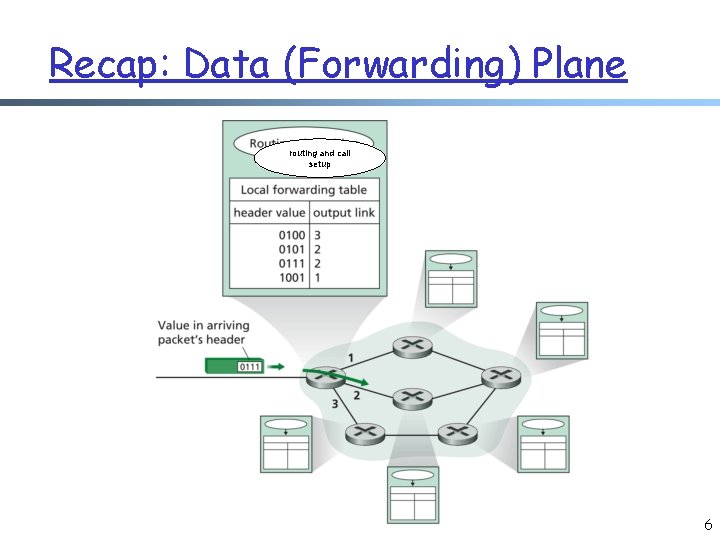
Recap: Data (Forwarding) Plane routing and call setup 6

Recap: Routing Design Space Routing Goal: determine “good” paths (sequences of routers) thru network from source to dest. r Routing has a large design space m who decides routing? • source routing: end hosts make decision • network routing: networks make decision m how many paths from source s to destination d? • multi-path routing • single path routing m does the route(s) provide Qo. S? • Qo. S • best effort, shortest path m will routing adapt to network traffic demand? • adaptive routing • static routing 7

Routing Design Space: Adaptive Routing r Routing has a large design space m who decides routing? • source routing: end hosts make decision • network routing: networks make decision m how many paths from source s to destination d? • multi-path routing • single path routing m does the route(s) provide Qo. S? • Qo. S • best effort, shortest path m will routing adapt to network traffic demand? • adaptive routing • static routing 8

Shortest/Lowest Cost Path Routing 5 A 2 1 B 2 D 3 3 1 C 5 F 1 E 2 r Represent network as a graph, with positive costs assigned to network links r The path from a source to a destination chosen by the routing protocol is a shortest (lowest cost) path among all possible paths 9

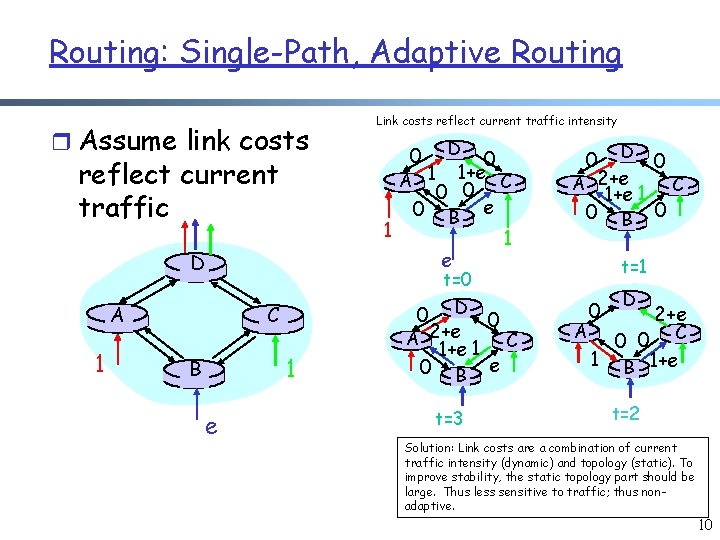
Routing: Single-Path, Adaptive Routing r Assume link costs reflect current traffic 1 0 1+e A 1 C 0 0 0 B e 1 0 D 0 A 2+e 1 C 0 B 0 t=1 t=0 D 1 e D e C B 0 1 D A Link costs reflect current traffic intensity 0 0 2+e A 1+e 1 C 0 B e t=3 A 0 D 2+e 0 0 C 1 B 1+e t=2 Solution: Link costs are a combination of current traffic intensity (dynamic) and topology (static). To improve stability, the static topology part should be large. Thus less sensitive to traffic; thus nonadaptive. 10

Example: Cisco Proprietary Recommendation on Link Cost r Link metric: m metric = [K 1 * bandwidth-1 + (K 2 * bandwidth-1) / (256 - load) + K 3 * delay] * [K 5 / (reliability + K 4)] By default, k 1=k 3=1 and k 2=k 4=k 5=0. The default composite metric for EIGRP, adjusted for scaling factors, is as follows: BWmin is in kbps and the sum of delays are in 10 s of microseconds. EIGRP : Enhanced Interior Gateway Routing Protocol 11

Example: EIGRP Link Cost r The bandwidth and delay for an Ethernet interface are 10 Mbps and 1 ms, respectively. r The calculated EIGRP BW metric is as follows: 256 × 107/BW = 256 × 107/10, 000 m = 256 × 10000 m = 256000 m 5 A 2 1 B 2 D 3 C 3 1 1 E 5 F 2 12

Outline q Admin and recap Ø Distance vector protocols 13

Distance Vector Routing 5 r Basis of RIP, IGRP, EIGRP routing protocols r Distributed alg to compute shortest paths A 2 1 B 2 D 3 C 3 1 1 E m conceptually, runs for each destination separately • hence we consider one dest only m state: each node maintains a current estimate of distance to the destination • di denotes the distance estimation from node i to dest m update rule: based on Bellman-Ford alg. 5 2 F

Distance Vector Routing: Update r At node i, the basic update rule destination where - di denotes the distance estimation from i to the destination, - N(i) is set of neighbors of node i, and - dij is the distance of the direct link from i to j j i 15

Synchronous Bellman-Ford (SBF) 7 A 10 B 8 1 C 2 r Nodes update in rounds: E 2 D m there is a global clock; m at the beginning of each round, each node sends its estimate to dest to all of its neighbors; m at the end of the round, updates its estimation A B E C D 16

Outline q Network overview q Control plane: routing overview Ø Distance vector protocols Ø synchronous Bellman-Ford (SBF) - SBF/ 17

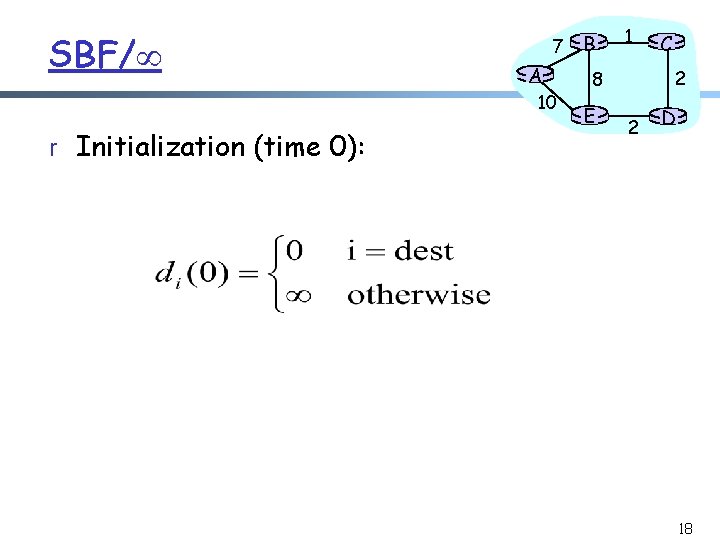
SBF/ 7 A 10 r Initialization (time 0): B 1 2 8 E C 2 D 18

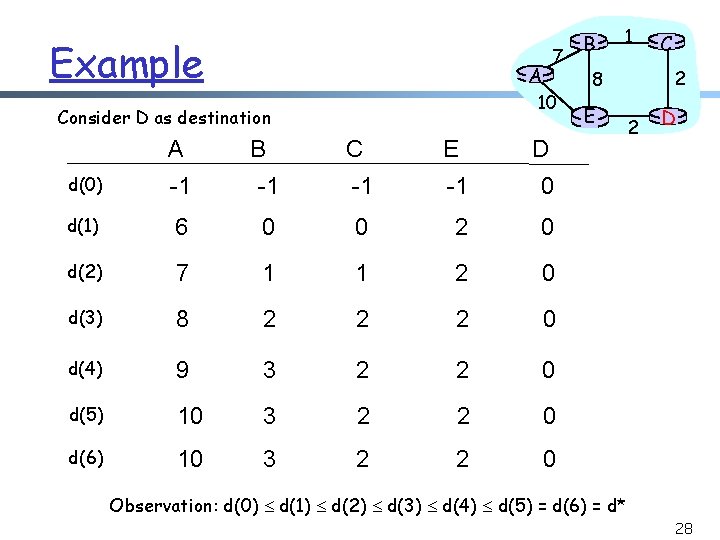
Example 7 A Consider D as destination; d(t) is a vector consisting of estimation of each node at round t 10 A B C E D d(0) 0 d(1) 2 2 0 d(2) 12 3 2 2 0 d(3) 10 3 2 2 0 d(4) 10 3 2 2 0 Observations: - d(0) d(1) d(2) d(3) d(4) - After a few iterations d(n) = d(n+1) = d* B 1 2 8 E C 2 D 19

A Nice Property of SBF: Monotonicity r Consider two configurations d(t) and d’(t) r If d(t) d’(t) m i. e. , each node has a higher estimate in d than in d’, r then d(t+1) d’(t+1) m i. e. , each node has a higher estimate in d than in d’ after one round of synchronous update. 20

Correctness of SBF/ r Claim: di(h) is the length Li(h) of a shortest path from i to the destination using ≤ h hops m m base case: h = 0 is trivially true assume true for ≤ h, i. e. , Li(h)= di(h), Li(h-1)= di(h-1), … 21

Correctness of SBF/ r consider ≤ h+1 hops: since di(h) ≤ di(h-1) 22

Bellman Equation r We referred to the update rules as Bellman equations (BE): where d. D = 0. - SBF/ solves the equations in a distributed way - Does the equation have a unique solution (i. e. , the shortest path one)? 23

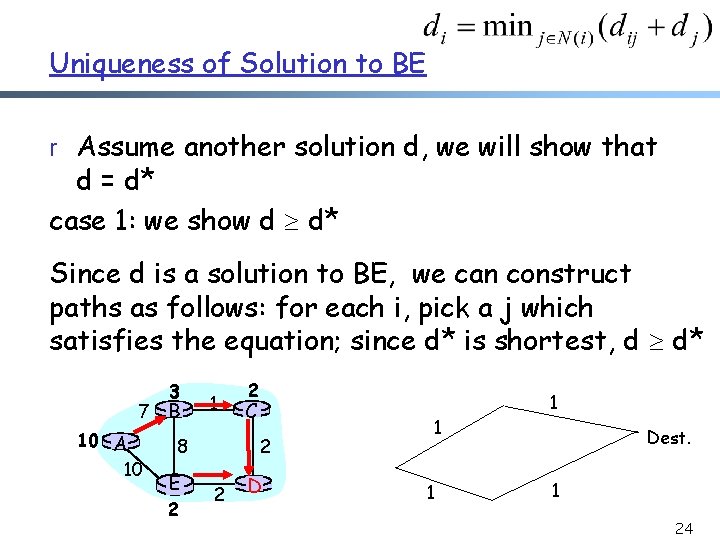
Uniqueness of Solution to BE r Assume another solution d, we will show that d = d* case 1: we show d d* Since d is a solution to BE, we can construct paths as follows: for each i, pick a j which satisfies the equation; since d* is shortest, d d* 7 10 A 10 3 B 1 2 C 2 8 E 2 2 D 1 1 1 Dest. 1 24

Uniqueness of Solution to BE Case 2: we show d ≤ d* assume we run SBF with two initial configurations: one is d m another is SBF/ (d ), m -> monotonicity and convergence of SBF/ imply that d ≤ d* 25

Outline q Network overview q Control plane: routing overview Ø Distance vector protocols Ø synchronous Bellman-Ford (SBF) - SBF/-1 26

SBF at another Initial Configuration: SBF/-1 7 A 10 B 1 2 8 E C 2 D r Initialization (time 0): 27

Example A 10 Consider D as destination A 7 B C E D d(0) -1 -1 0 d(1) 6 0 0 2 0 d(2) 7 1 1 2 0 d(3) 8 2 2 2 0 d(4) 9 3 2 2 0 d(5) 10 3 2 2 0 d(6) 10 3 2 2 0 B 1 2 8 E C 2 D Observation: d(0) d(1) d(2) d(3) d(4) d(5) = d(6) = d* 28

Correctness of SBF/-1 r SBF/-1 converges due to monotonicity r At equilibrium, SBF/-1 satisfies Bellman equations: where d. D = 0. r Another solution is shortest path solution d* r Since there is a unique solution to the BE equations; thus SBF/-1 converges to shortest path 29

Discussion r How do you prove that SBF converges under other non-negative initial conditions? 30

Toolbox r A key technique for proving convergence (liveness) of distributed protocols: two extreme configurations to sandwich any real configurations 31

Discussion r Problem of SBF? A B E C D 32

Outline q Network overview q Control plane: routing overview Ø Distance vector protocols o synchronous Bellman-Ford (SBF) Ø asynchronous Bellman-Ford (ABF) 33

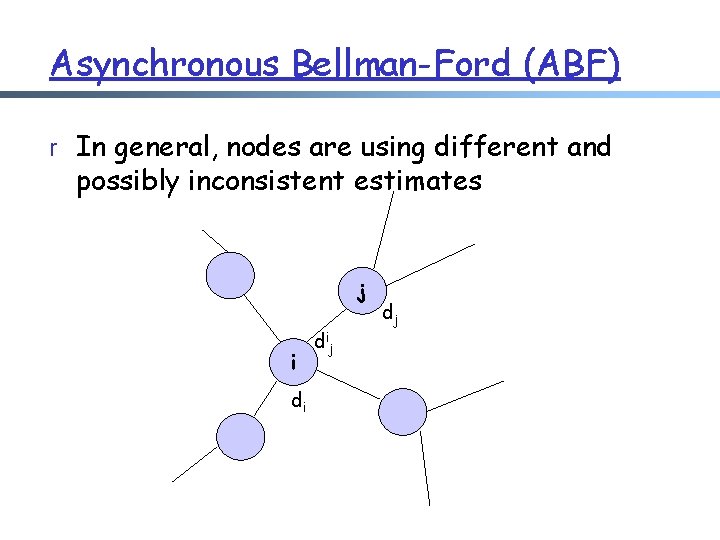
Asynchronous Bellman-Ford (ABF) r No notion of global iterations m each node updates at its own pace r Asynchronously each node i computes using last received value dij from neighbor j. r Asyncrhonously node j sends its estimate to its neighbor i: m there is an upper bound on the delay of estimate packets (no worry for out of order)

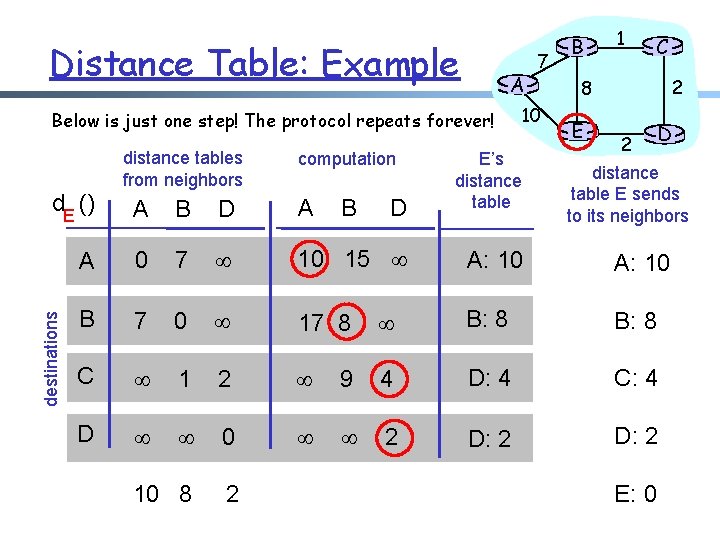
Distance Table: Example A Below is just one step! The protocol repeats forever! distance tables from neighbors computation A B D A A 0 7 10 15 B 7 0 17 8 C 1 2 D 0 10 8 2 destinations d. E () B D 7 10 E’s distance table B 1 C 2 8 E 2 D distance table E sends to its neighbors A: 10 B: 8 9 4 D: 4 C: 4 2 D: 2 E: 0

Asynchronous Bellman-Ford (ABF) r In general, nodes are using different and possibly inconsistent estimates j i di di j dj

Asynchronous Bellman-Ford (ABF) r ABF will eventually converge to the shortest path m links can go down and come up – but if topology is stabilized after some time t, ABF will eventually converge to the shortest path ! r If the network is connected, then ABF converges in finite amount of time, if conditions are met

ABF Convergence r There are too many different “runs” of ABF, so need to use monotonicity r Consider two sequences: • SBF/ ; call the sequence U() • SBF/-1; call the sequence L()

System State j i where can distance estimate from node j appear?

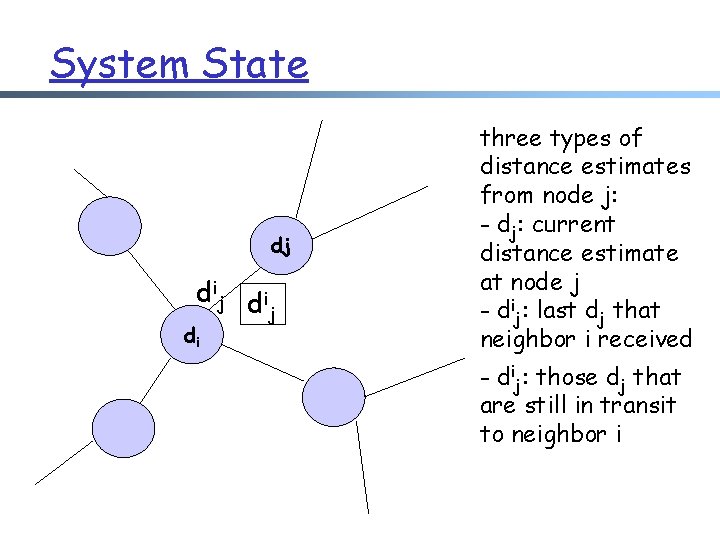
System State dj d i j di three types of distance estimates from node j: - dj: current distance estimate at node j - dij: last dj that neighbor i received - dij: those dj that are still in transit to neighbor i

ABF Convergence r Consider the time when the topology is stabilized as time 0 r U(0) and L(0) provide upper and lower bound at time 0 on all corresponding elements of states Lj (0) ≤ dj ≤ Uj (0) for all dj state at node j m Lj (0) ≤ dij ≤ Uj (0) m Lj (0) ≤ update messages dij ≤ Uj (0) m

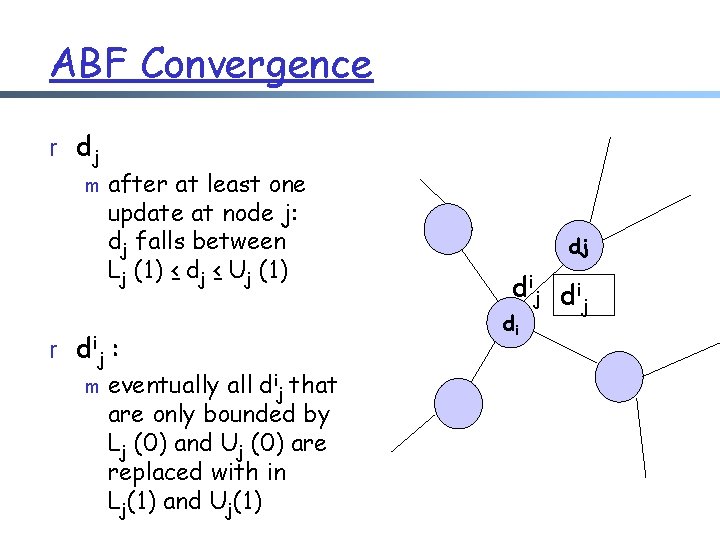
ABF Convergence r dj m after at least one update at node j: dj falls between Lj (1) ≤ dj ≤ Uj (1) r d ij : m eventually all dij that are only bounded by Lj (0) and Uj (0) are replaced with in Lj(1) and Uj(1) dj d i j di

Asynchronous Bellman-Ford: Summary r Distributed: each node communicates its routing table to its directly-attached neighbors r Iterative: continues periodically or when link changes, e. g. detects a link failure r Asynchronous: nodes need not exchange info/iterate in lock step! r Convergence in finite steps, independent of initial condition if network is connected

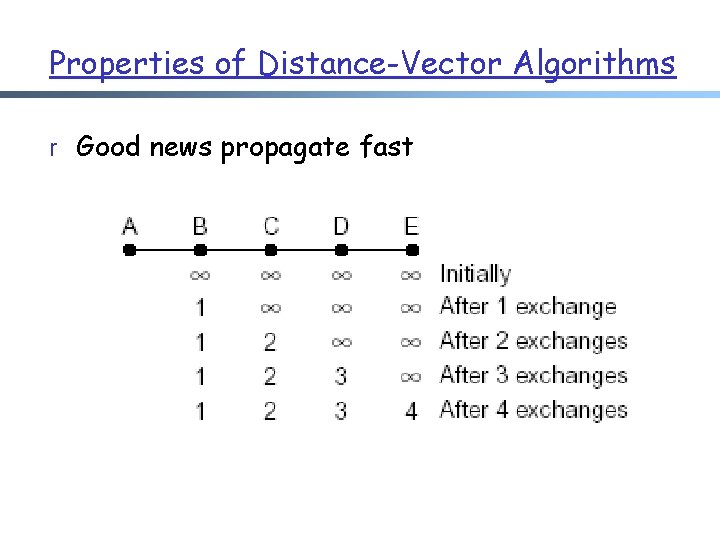
Properties of Distance-Vector Algorithms r Good news propagate fast

Properties of Distance-Vector Algorithms r Bad news propagate slowly (link A-B broke) r This is called the counting-to-infinity problem Question: why does counting-to-infinity happen?

What is a Routing Loop? r A routing loop is a global state (consisting of the nodes’ local states) at a global moment (observed by an oracle) such that there exist nodes A, B, C, … E such that A (locally) thinks B as down stream, B thinks C as down stream, … E thinks A as down stream r Counting-to-infinity because of routing loops 46

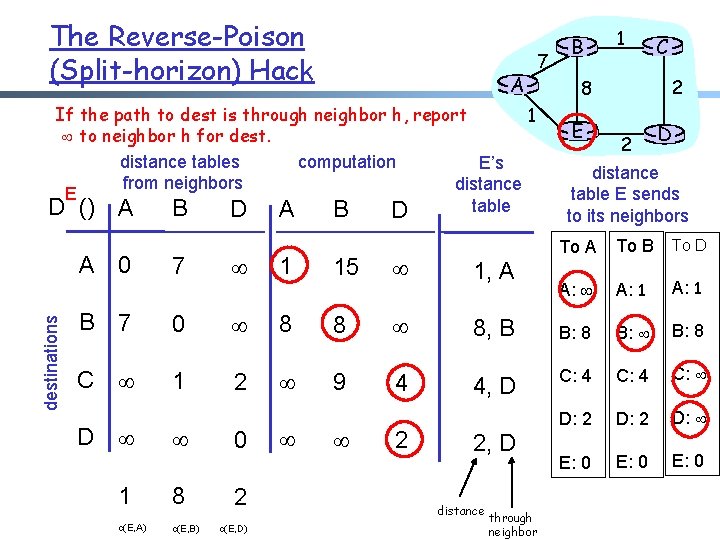
The Reverse-Poison (Split-horizon) Hack A 7 If the path to dest is through neighbor h, report 1 to neighbor h for dest. distance tables computation E’s from neighbors distance E table D () A B D destinations A 0 7 1 15 1, A B 1 2 8 E C 2 D distance table E sends to its neighbors To A To B To D A: A: 1 B 7 0 8 8 8, B B: 8 B: B: 8 C 1 2 9 4 4, D C: 4 C: D: 2 D: E: 0 D 0 1 8 2 c(E, A) c(E, B) c(E, D) 2 2, D distance through neighbor

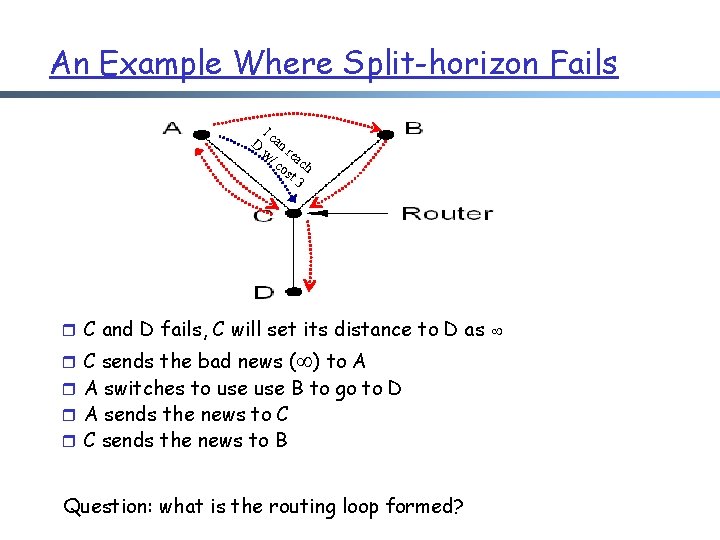
An Example Where Split-horizon Fails Ic 1 D an w/ rea c c 1 ost 3 h 1 1 r C and D fails, C will set its distance to D as r C sends the bad news ( ) to A r A switches to use B to go to D r A sends the news to C r C sends the news to B Question: what is the routing loop formed?

Outline q Admin and recap Ø Distance vector protocols o synchronous Bellman-Ford (SBF) o asynchronous Bellman-Ford (ABF) Ø RIP, EIGRP 49

Example: RIP ( Routing Information Protocol) r Distance vector r Included in BSD-UNIX Distribution in 1982 r Link cost: 1 r Distance metric: # of hops r Distance vectors m m exchanged every 30 sec via Response Message (also called advertisement) using UDP each advertisement: route to up to 25 destination nets

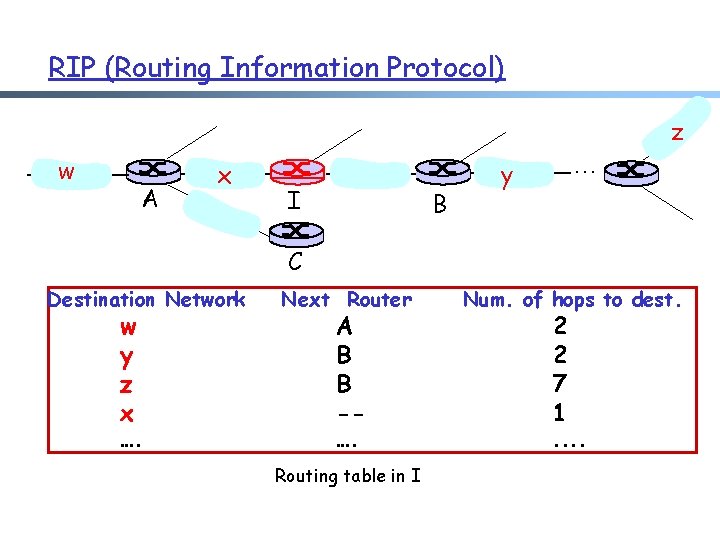
RIP (Routing Information Protocol) z w A x I B . . . y C Destination Network w y z x …. Next Router Num. of hops to dest. …. . . A B B -- Routing table in I 2 2 7 1

RIP: Link Failure and Recovery If no advertisement heard after 180 sec --> neighbor/link declared dead m routes via neighbor invalidated m m new advertisements sent to neighbors in turn send out new advertisements (if tables changed) m link failure info quickly propagates to entire net m reverse-poison used to prevent ping-pong loops m set infinite distance = 16 hops (why? )

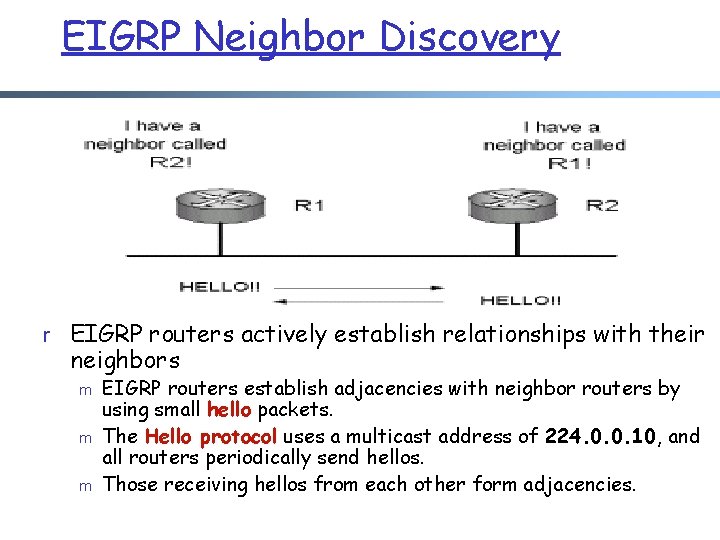
EIGRP Neighbor Discovery r EIGRP routers actively establish relationships with their neighbors m m m EIGRP routers establish adjacencies with neighbor routers by using small hello packets. The Hello protocol uses a multicast address of 224. 0. 0. 10, and all routers periodically send hellos. Those receiving hellos from each other form adjacencies.

Default Hello Intervals and Hold Time for EIGRP

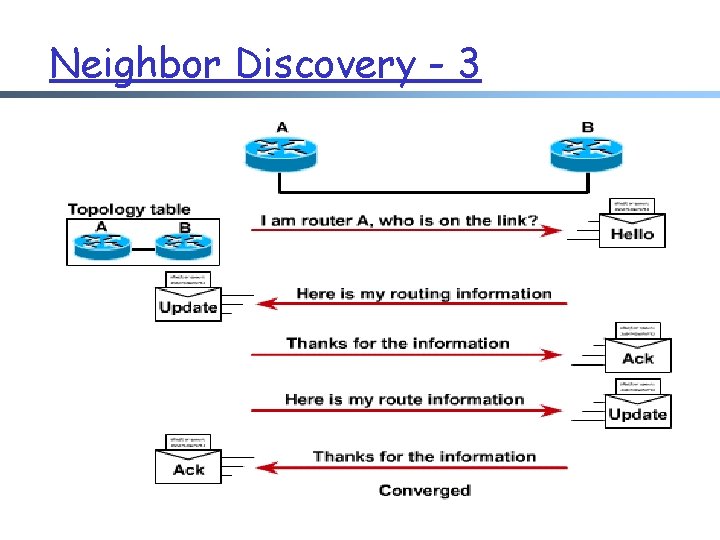
Neighbor Discovery - 3 55

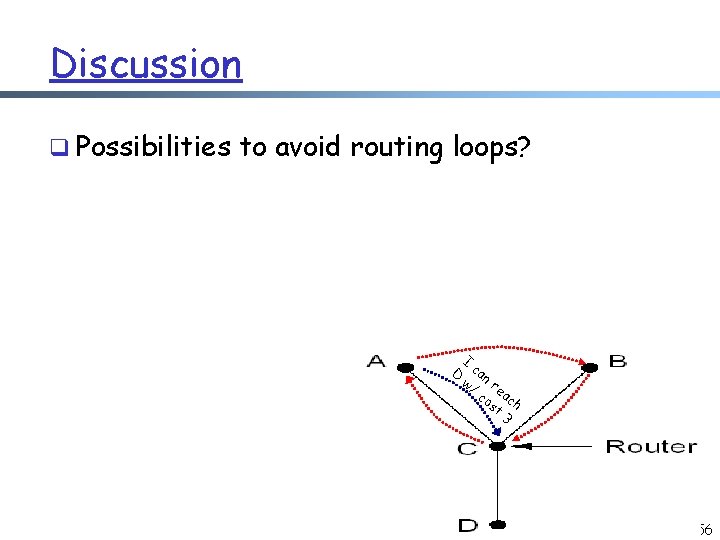
Discussion q Possibilities to avoid routing loops? I D can w/ r co eac st h 3 56