Computer Logic Design Waqar Lecture 03 Copyrights Dr
























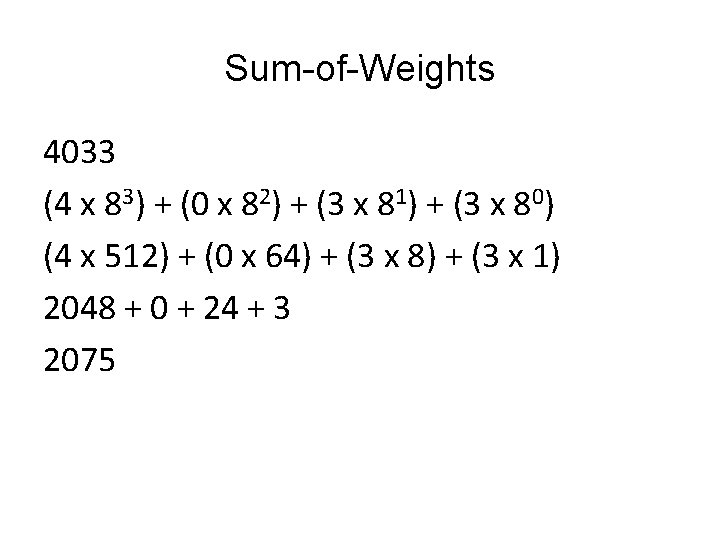












- Slides: 47

Computer Logic & Design Waqar Lecture 03 Copyrights: Dr Waseem Ikram

Recap • Number System Conversion – Sum-of-Weights for converting to decimal – Repeated division for converting from decimal • Binary Arithmetic – Similar to Decimal Arithmetic – Multiplying by a constant by shifting left – Dividing by a constant by shifting right

Recap • Representing Numbers – Unsigned – Signed Magnitude – 2’s Complement

2’s Complement form • 1’s complement form • 2’s complement form Binary number 1’s complement 2’s complement 01101(13) 10010 + 1 10011(-13)

Range of Numbers • Unsigned – Positive Numbers Only (0 to 7) – 3 -bit • Signed Magnitude – Positive & Negative Numbers (-7 to 7) – 4 -bit • 2’s Complement – Positive & Negative Numbers (-8 to 7) – 4 -bit

Range & Overflow • • 2 + 7 using 3 -bit unsigned binary? 9 overflow? 2 – 7? Can not represent -7 in unsigned binary

Range and Overflow • If an addition operation produces a result that exceeds the range of the number system, overflow is said to occur. • If the sum of two positive numbers yields a negative result, the sum has overflowed. • If the sum of two negative numbers yields a positive result, the sum has overflowed. • Otherwise, the sum has not overflowed. • Carryout without overflow. Sum is correct

Addition and Subtraction with 2’s Complement 0101 0010 0111 +5 +2 +7 0101 1110 10011 +5 -2 +3 1011 1110 11001 -5 -2 -7 1011 0010 1101 -5 +2 -3

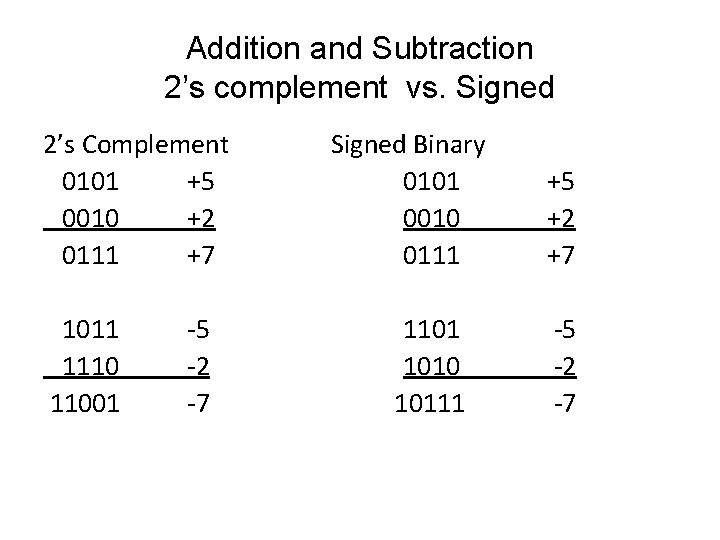
Addition and Subtraction 2’s complement vs. Signed 2’s Complement 0101 +5 0010 +2 0111 +7 1011 1110 11001 -5 -2 -7 Signed Binary 0101 0010 0111 1101 1010 10111 +5 +2 +7 -5 -2 -7

Addition and Subtraction 2’complement vs. Signed 0101 1110 10011 +5 -2 +3 1011 0010 1101 -5 +2 -3 0101 1010 1111 1101 0010 1111 +5 -2 +3 -5 +2 -3

Range and Overflow 1011 -5 1101 -3 11000 -8 1011 1100 10111 -5 -4 -9 0101 0100 1001 +5 +4 +9

Range of Binary Numbers • • • Processors can handle 64 -bit unsigned binary values. Maximum unsigned decimal number is 18. 446 x 1018 How to represent larger numbers? How to represent very small numbers? How to represent numbers with integer part and fraction part?

Hexadecimal Number System • Base 16 • 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F • Representing Binary in compact form 11011000001102 = 1 B 06 H

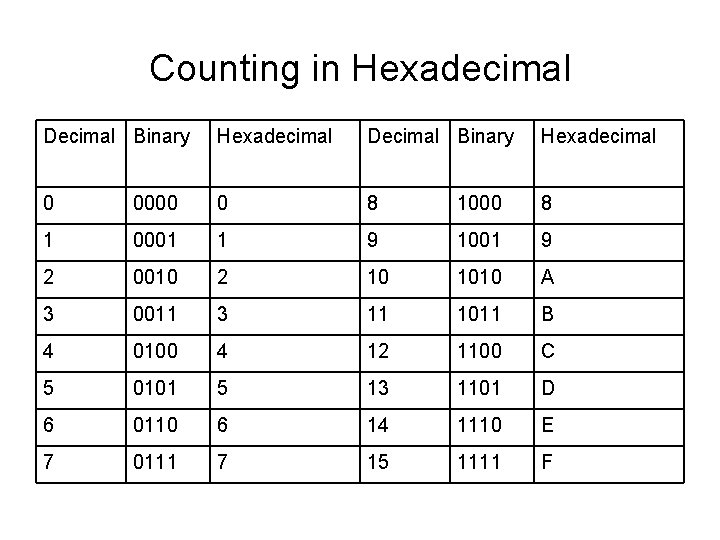
Counting in Hexadecimal Decimal Binary Hexadecimal 0 0000 0 8 1000 8 1 0001 1 9 1001 9 2 0010 2 10 1010 A 3 0011 3 11 1011 B 4 0100 4 12 1100 C 5 0101 5 13 1101 D 6 0110 6 14 1110 E 7 0111 7 15 1111 F

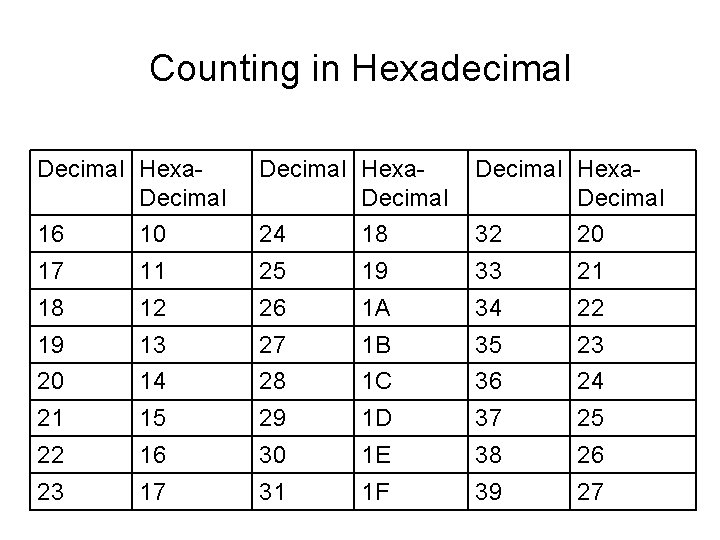
Counting in Hexadecimal Decimal Hexa. Decimal 16 10 24 18 32 20 17 11 25 19 33 21 18 12 26 1 A 34 22 19 13 27 1 B 35 23 20 14 28 1 C 36 24 21 15 29 1 D 37 25 22 16 30 1 E 38 26 23 17 31 1 F 39 27

Binary-Hexadecimal Conversion • Binary to Hexadecimal Conversion – 110101110010110 – 1101 0110 1011 1001 0110 –D 6 B 9 6 • Hexadecimal to Binary Conversion – FD 13 – 1111 1101 0011

Decimal-Hexadecimal Conversion • Decimal to Hexadecimal Conversion • Indirect Method – Decimal →Binary → Hexadecimal • Repeated Division by 16

Decimal-Hexadecimal Conversion • Hexadecimal to Decimal Conversion • Indirect Method – Hexadecimal →Binary → Decimal • Sum-of-Weights

Hexadecimal Addition & Subtraction • Hexadecimal Addition – Carry generated • Hexadecimal Subtraction – Borrow weight 16

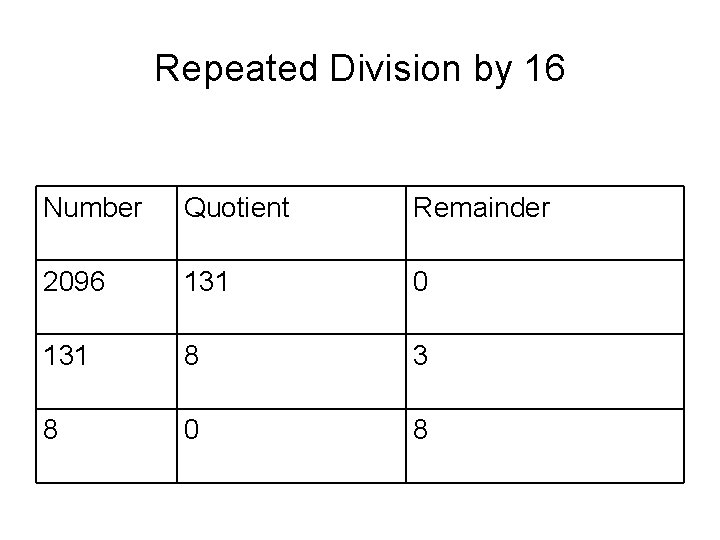
Repeated Division by 16 Number Quotient Remainder 2096 131 0 131 8 3 8 0 8

Sum-of-Weights CA 02 (C x 163) + (A x 162) + (0 x 161) + (2 x 160) (12 x 163) + (10 x 162) + (0 x 161) + (2 x 160) (12 x 4096) + (10 x 256) + (0 x 16) + (2 x 1) 49152 + 2560 + 2 51714

Hexadecimal Addition Carry 1 + 2 AC 6 92 B 5 BD 7 B 6+5=11 d Bh C+B=23 d 17 h A+2+1=13 d Dh 2+9=11 d Bh

Hexadecimal Subtraction Borrow - 111 92 B 5 2 AC 6 67 EF 21 -6=15 d = Fh 26 -C=14 d = Eh 17 -A=7 d = 7 h 8 -2=6 d = 6 h

Octal Number System • Base 8 • 0, 1, 2, 3, 4, 5, 6, 7 • Representing Binary in compact form – 11011000001102 = 154068

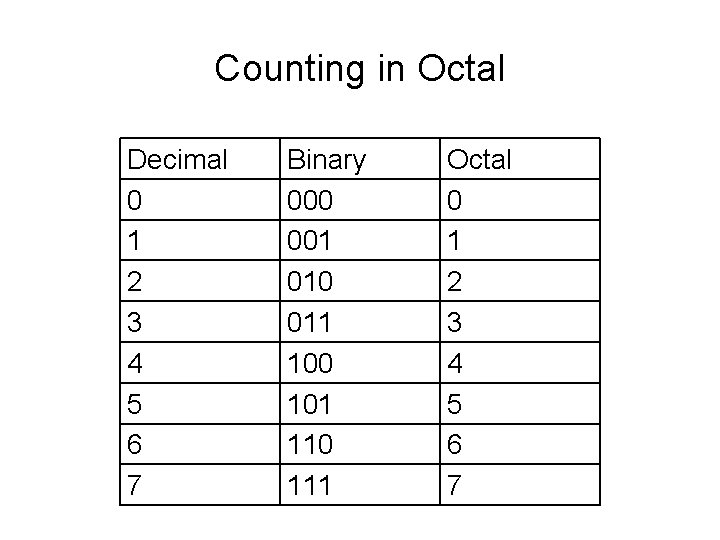
Counting in Octal Decimal 0 1 2 3 4 5 6 7 Binary 000 001 010 011 100 101 110 111 Octal 0 1 2 3 4 5 6 7

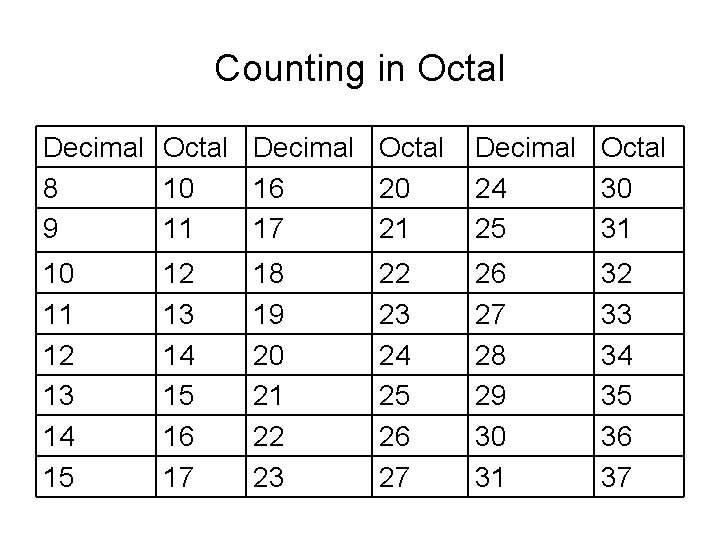
Counting in Octal Decimal Octal 8 10 16 20 9 11 17 21 Decimal Octal 24 30 25 31 10 11 12 13 14 15 26 27 28 29 30 31 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 32 33 34 35 36 37

Binary-Octal Conversion • Binary to Octal Conversion – 110101110010110 – 011 010 101 110 010 110 – 3 2 6 5 6 2 6 • Octal to Binary Conversion – 1726 – 001 111 010 110

Decimal-Octal Conversion • Decimal to Octal Conversion • Indirect Method – Decimal →Binary → Octal • Repeated Division by 8

Decimal-Octal Conversion • Octal to Decimal Conversion • Indirect Method – Octal →Binary → Decimal • Sum-of-Weights

Octal Addition & Subtraction • Octal Addition – Carry generated • Octal Subtraction – Borrow weight 8

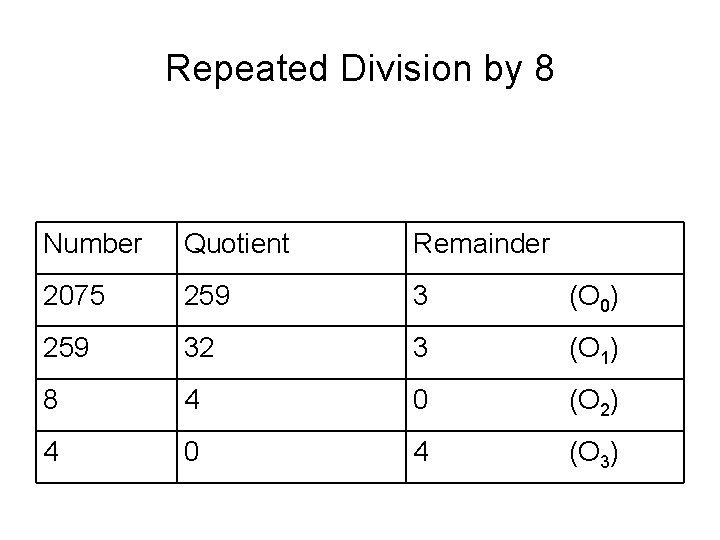
Repeated Division by 8 Number Quotient Remainder 2075 259 3 (O 0) 259 32 3 (O 1) 8 4 0 (O 2) 4 0 4 (O 3)
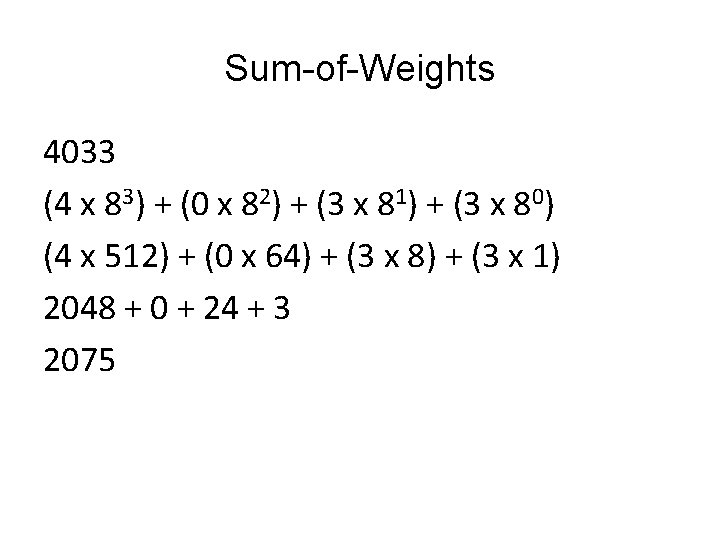
Sum-of-Weights 4033 (4 x 83) + (0 x 82) + (3 x 81) + (3 x 80) (4 x 512) + (0 x 64) + (3 x 8) + (3 x 1) 2048 + 0 + 24 + 3 2075

Octal Addition Carry 1 7602 + 5771 15573 2+1=3 d= 3 O 0+7=7 d= 7 O 6+7=13 d= 15 O 1+7+5=13 d =15 O

Octal Subtraction Borrow - 11 7602 5771 1611 2 -1=1 d 1 O 8 -7=1 d 1 O 13 -7=6 d 6 O 6 -5=1 d 1 O

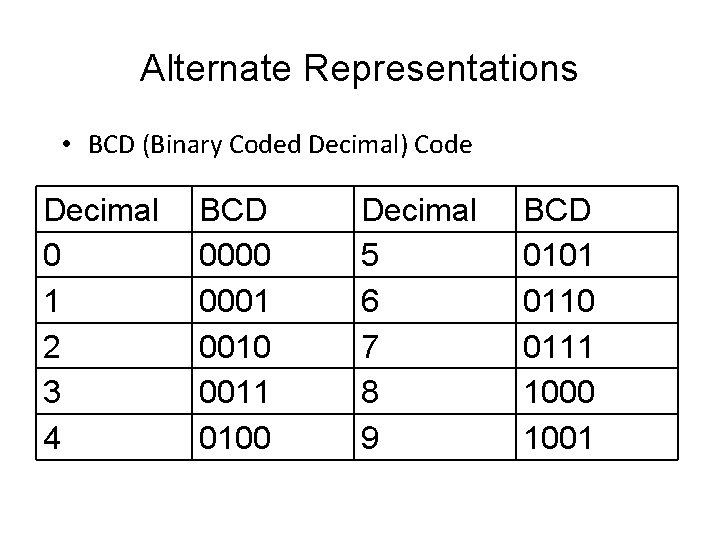
Alternate Representations • BCD Code • Gray Code

Alternate Representations • BCD (Binary Coded Decimal) Code Decimal 0 1 2 3 4 BCD 0000 0001 0010 0011 0100 Decimal 5 6 7 8 9 BCD 0101 0110 0111 1000 1001

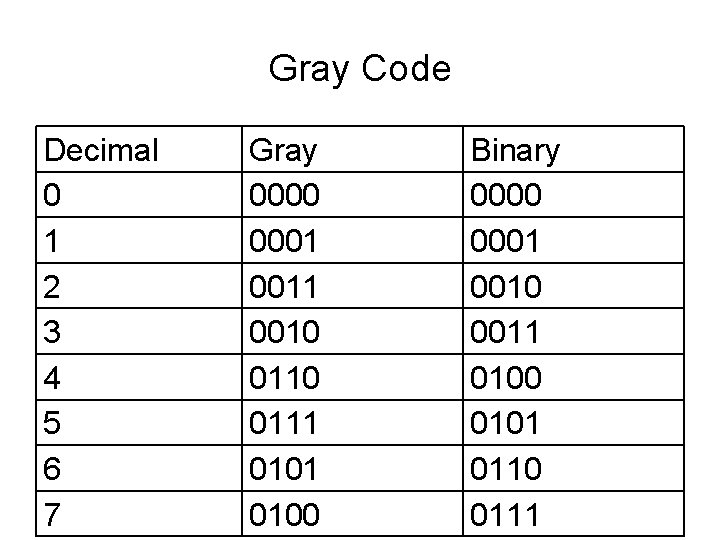
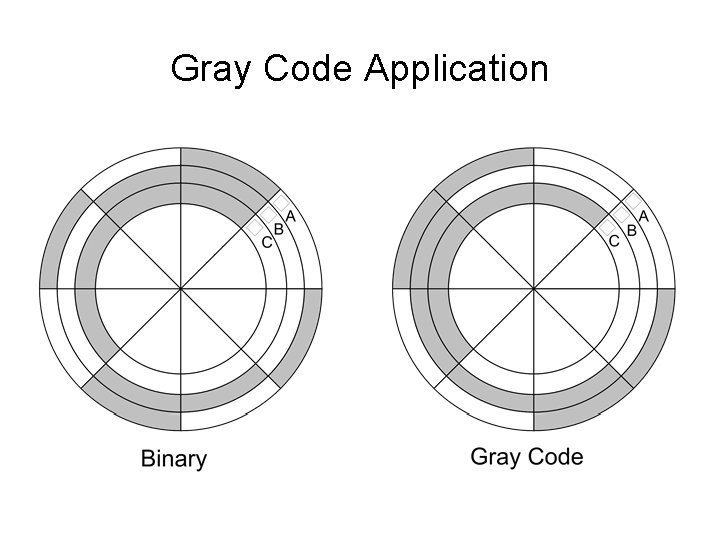
Gray Code • Binary Code more than 1 bit change • Electromechanical applications of digital systems restrict bit change to 1 – Shaft encoders – Braking Systems • Un-Weighted Code

Gray Code Decimal 0 1 2 3 4 5 6 7 Gray 0000 0001 0010 0111 0100 Binary 0000 0001 0010 0011 0100 0101 0110 0111

Gray Code Application

Alphanumeric Code • • Numbers, Characters, Symbols ASCII 7 -bit Code American Standard Code for Information Interchange 10 Numbers (0 -9) 26 Lower Case Characters (a-z) 26 Upper Case Characters (A-Z) Punctuation and Symbols 32 Control Characters

ASCII Code • • Numbers 0 to 9 ASCII 0110000 (30 h) to 0111001 (39 h) Alphabets a to z ASCII 1100001 (61 h) to 1111010 (7 Ah) Alphabets A to Z ASCII 1000001 (41 h) to 1011010 (5 Ah) Control Characters ASCII 0000000 (0 h) to 0011111 (1 Fh)

Alphanumeric Code • Extended ASCII 8 -bit Code • Additional 128 Graphic characters • Unicode 16 -bit Code

Error Detection • Digital Systems are very Reliable • Errors during storage or transmission • Parity Bit – Even Parity – Odd Parity

Odd Parity Error Detection • • Original data 10011010 With Odd Parity 110011010 1 -bit error 11010 Number of 1 s even indicates 1 -bit error 2 -bit error 110110010 Number of 1 s odd no error indicated 3 -bit error 10010 Number of 1 s even indicates error

Summary • 2’s Complement • Range and Overflow

Summary • Hexadecimal Number System – Binary-Hexadecimal Conversion – Decimal-Hexadecimal Conversion • Octal Number System – Binary-Octal Conversion – Decimal-Octal Conversion

Summary • Alternate Representations – BCD Code – Gray Code • Alphanumeric Codes – ASCII • Error Detection – Parity Bit