Computer Language Theory Chapter 1 Regular Languages Dr

Computer Language Theory Chapter 1: Regular Languages Dr. Gary Weiss, January 27 2008 1

Chapter 1. 1: Finite Automata Dr. Gary Weiss, January 27 2008 2

What is a Computer? n Not a simple question to answer precisely n n We start with a computational model n n Computers are quite complicated Different models will have different features and may match a real computer better in some ways and worse in others Our first model is the finite state machine or finite automata Dr. Gary Weiss, January 27 2008 3

Finite Automata n Models of computers with extremely limited memory Many simple computers have extremely limited memories and are in fact finite state machines n Can you name any? Hint: several are in this building but have nothing specifically to do with our department n n Vending machine n Elevator n Thermostat n Automatic door at supermarket Dr. Gary Weiss, January 27 2008 4

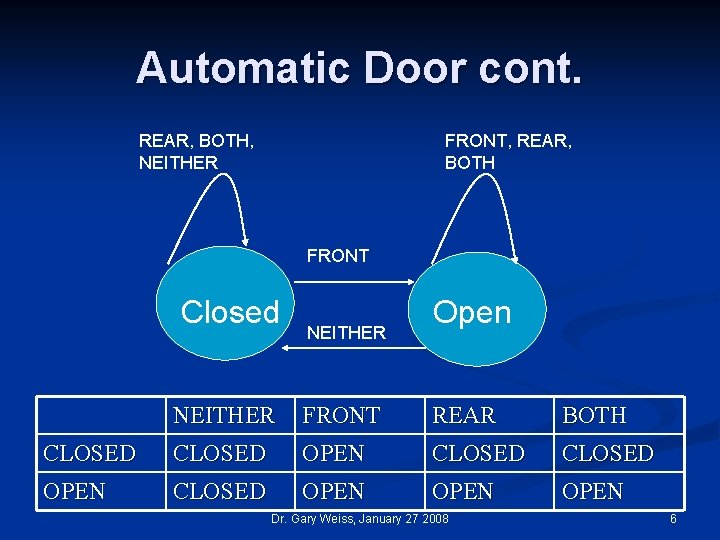
Automatic Door n What is the desired behavior? Describe the actions and then list the states. n n n Person approaches, door should open Door should stay open while person going thru Door should shut if no one near doorway States are open and closed More details about automatic door n n Front pad Door Rear Pad Describe behavior now n n n Hint: action depends not just on what happens, but what state you are currently in If you walk thru door should stay open when you are on rear pad But if door is closed and someone steps on rear pad, door does not open Dr. Gary Weiss, January 27 2008 5

Automatic Door cont. REAR, BOTH, NEITHER FRONT, REAR, BOTH FRONT Closed NEITHER Open NEITHER FRONT REAR BOTH CLOSED OPEN CLOSED OPEN Dr. Gary Weiss, January 27 2008 6

More on Finite Automata n How many bits of data does this FSM store? n 1 bit: open or closed What about state information for elevators, thermostats, vending machines, etc? n FSM used in speech processing, optical character recognition, etc. n Have you implemented FSM? What? n n I have implemented network protocols and expert systems for diagnosing Dr. Gary Weiss, January 27 2008 telecommunication equipment problems 7

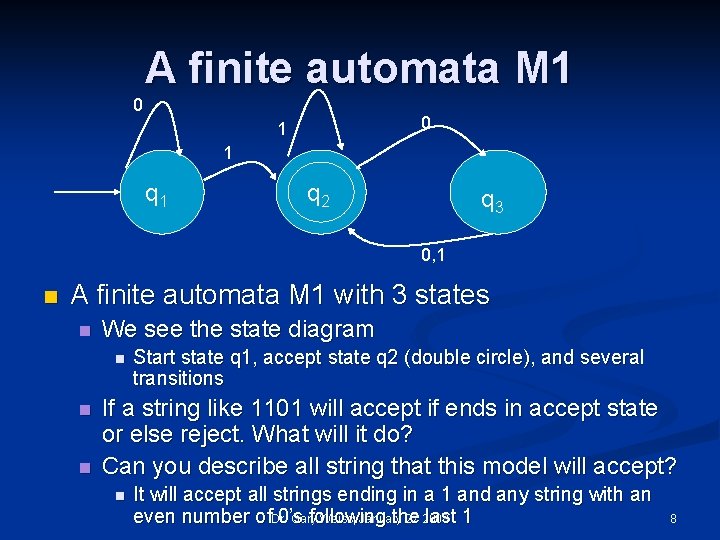
A finite automata M 1 0 0 1 1 q 2 q 3 0, 1 n A finite automata M 1 with 3 states n We see the state diagram n n n Start state q 1, accept state q 2 (double circle), and several transitions If a string like 1101 will accept if ends in accept state or else reject. What will it do? Can you describe all string that this model will accept? n It will accept all strings ending in a 1 and any string with an even number of. Dr. 0’s following the last 1 Gary Weiss, January 27 2008 8

Formal Definition of Finite Automata n A finite automata is a 5 -tuple (Q, , δ, q 0, F) Q is a finite set called states n is a finite set called the alphabet n δ : Q x Q is the transition function n q 0 Q is the start state n F Q is the set of accept states n Dr. Gary Weiss, January 27 2016 9

Describe M 1 using Formal Definition 0 1 q 1 q 2 q 3 0, 1 n M 1 = (Q, , δ, q 0, F) n n n Q= = δ: Start state: F= Dr. Gary Weiss, January 27 2008 10

Describe M 1 using Formal Definition 0 0 1 1 q 2 q 3 0, 1 n M 1 = (Q, , δ, q 0, F) n n Q = {q 1, q 2, q 3} = {0, 1} q 1 is the start state F = {q 2} q 1 q 2 q 3 0 q 1 q 3 q 2 Transition function δ Dr. Gary Weiss, January 27 2008 1 q 2 q 2 11

The Language of M 1 n If A is the set of all strings that a machine M accepts, then A is the language of M L(M) = A n We also say that M recognizes A or M accepts A n A machine may accept many strings, but only one language n Convention: M accepts string and recognizes a language n Dr. Gary Weiss, January 27 2008 12

What is the Language of M 1? L(M 1) = A or M 1 recognizes A n What is A? n A = {w | ……. } n A = {w| w contains at least one 1 and an even number of 0’s follows the last 1} n Dr. Gary Weiss, January 27 2008 13

What is the Language of M 2? 0 1 1 q 2 0 n M 2 = {{q 1, q 2}, {0, 1}, δ, q 1, {q 2}} I leave δ as an exercise n What is the language of M 2? n n L(M 2) = {w| ? } n L(M 2) = {w| w ends in a 1} Dr. Gary Weiss, January 27 2008 14

What is the Language of M 3? 0 1 1 q 2 0 n n M 3 is M 2 with different start state What is the language of M 3? n n n L(M 3) = {w| ? } L(M 3) = {w| w ends in 0} [Not quite right! Why? ] L(M 3) = {w| w is the empty string ε or ends in 0} Dr. Gary Weiss, January 27 2008 15

What is the Language of M 4 is a 5 state automata (Figure 1. 12 on page 38) n What does M 4 accept? n All strings that start and end with a or start and end with b n More simply, language is all string starting and ending with the same symbol n n Note that length of 1 is okay Dr. Gary Weiss, January 27 2008 16

Construct M 5 to do Modulo Arithmetic Let = {RESET, 0, 1, 2} n Construct M 5 to accept a string only if the sum of each input symbol is a multiple of 3 and RESET sets the sum back to 0 (1. 13, page 39) n Dr. Gary Weiss, January 27 2008 17

Now Generalize M 5 n Generalize M 5 to accept if sum of symbols is a multiple of i instead of 3 n ({q 0, q 1, q 2, q 3, …, qi-1} , {0, 1, 2, RESET}, δ, q 0) n n n δi(qj, 0) = qj δi(qj, 1) = qk where k=j+1 modulo i δi(qj, 2) = qk where k=j+2 modulo i δi(qj, RESET) = qo Note: as long as i is finite, we are okay and only need finite memory (# of states) Could you generalize on = {1, 2, 3, …k}? Dr. Gary Weiss, January 27 2008 18

Formal Definition of Accept n Definition of M accepting a string: Let M = (Q, , δ, q 0, F) be a finite automata and let w=w 1 w 2 …wn be a string where wi . n Then M accepts w if a sequence of states r 0, r 1, …, rn in Q exists with 3 conditions n n r 0=q 0 n δ(ri, wi+1) = ri+1, for i =0, 1, …, n-1 n rn F Dr. Gary Weiss, January 27 2008 19

Regular Languages n Definition: A language is called a regular language if some finite automata recognizes it That is, all of the strings in the language are accepted by some finite automata n Why should you expect proofs by construction coming up in your next homework? n Dr. Gary Weiss, January 27 2008 20

Designing Finite Automata n n You will need to design FA’s to accept a language Strategies n Determine what you need to remember (the states) n n n How many states to determine even/odd number of 1’s in an input? What does each state represent Set the start and finish states based on what each state represents Assign the transitions Check your solution: it should accept w L and not accept w not in L Dr. Gary Weiss, January 27 2008 21

You Try Designing FAs Design a FA to accept the language of binary strings where the number of 1’s is odd (page 43) n Design a FA to accept all string with 001 as a substring (page 44) n n n What do you need to remember Design a FA to accept a string with substring abab Dr. Gary Weiss, January 27 2008 22

Regular Operations n Let A and B be languages. We define 3 regular operations: Union: A B = {x| x A or x B} n Concatenation: A B where {xy| x A and y B} n Star: A* = {x 1 x 2 …. xk| k ≥ 0 and each xi A} n n Star is a unary operator on a single language n Star repeats a string 0 or more times Dr. Gary Weiss, January 27 2008 23

Examples of Regular Operations Let A = {good, bad} and B = {boy, girl} n Then what is: n n AUB n. A U n A B n. A n B = {good, bad, boy, girl} B = {goodboy, goodgirl, badboy, badgirl} A* n A* = {ε, good, bad, good, goodbad, badgood, goodgood, …} Dr. Gary Weiss, January 27 2008 24

Closure The natural numbers is closed under addition and multiplication (but not division and subtraction) n A collection of objects is closed under an operation if applying that operation to members of the collection returns an object in the collection n Dr. Gary Weiss, January 27 2008 25

Closure for Regular Languages Regular languages are closed under the 3 regular operators we just introduced n Can you look ahead to see why we care? n n If these operators are closed, then if we can implement each operator using a FA, then we can build a FA to recognize a regular expression Dr. Gary Weiss, January 27 2008 26

Closure of Union n Theorem 1. 25: The class of regular languages is closed under the union operation If A 1 and A 2 are regular languages then so is A 1 A 2 n How can we prove this? Use proof by construction. n n Assume M 1 accepts A 1 and M 2 accepts A 2 n Construct M 3 using M 1 and M 2 to accept A 1 A 2 n We need to simulate M 1 and M 2 running in parallel and stop if either reaches an accept state n Dr. Gary Weiss, January 27 2008 27 This last part is feasible since we can have multiple accept

Closure of Union II You need to generate a state to represent the state you would be in with M 1 and M 2 n Let M 1 = (Q 1, , δ 1, q 1, F 1) and M 2 = (Q 2, , δ 2, q 2, F 2) n Build M 3 as follows (we will do Q, , q 0, F, δ ): n Q = {(r 1, r 2)| r 1 Q and r 2 Q (Cartesian product) n stays the same but could more generally be 1 2 n q 0 is the pair (q , q. Weiss, Dr. 1 Gary 28 2) January 27 2008 n

Closure of Concatenation n Theorem 1. 26: The class of regular languages is closed under the concatenation operator If A 1 and A 2 are regular languages then so is A 1 A 2 n Can you see how to do this simply? n n Not trivial since cannot just concatenate M 1 and M 2, where start states of M 2 become the finish states of M 1 Because we do not accept a string as soon as it enters the finish state, we wait until string is done, so it can leave and come back n Thus we do know when to start using M 2 Dr. not Gary Weiss, January 27 2008 29 n

Chapter 1. 2: Nondeterminism Dr. Gary Weiss, January 27 2008 30

Nondeterminism n n n So far our FA is deterministic in that the state and next symbol determines the next state In a nondeterministic machine, several choices may exist DFA’s have one transition arrow per alphabet symbol, while NFAs have 0 or more for each and ε 0, 1 q 1 1 q 2 0, ε Dr. Gary Weiss, January 27 2008 1 q 3 q 4 31

How does an NFA Compute? n When there is a choice, all paths are followed n n n Think of it as cloning a process and continuing If there is no arrow, the path terminates and the clone dies (it does not accept if at an accept state when that happens) An NFA may have the empty string cause a transition The NFA accepts if any path is in the accept state Can also be modeled as a tree of possibilities An alternative way of thinking of this n n At each choice you make one guess of which way to go Dr. Gary Weiss, January 27 2008 right way to go 32 You magically always guess the

Try Computing This! 0, 1 q 1 n 1 q 2 0, ε 1 q 3 q 4 Try out 010110 n Is it accepted? n Yes n What is the language? n Strings containing a substring of 101 or 11 Dr. Gary Weiss, January 27 2008 33

Construct an NFA n Construct an NFA that accepts all string over {0, 1} with a 1 in the third position from the end n Hint: the NFA stays in the start state until it guesses that it is three places from the end Dr. Gary Weiss, January 27 2008 34

Construct an NFA n Construct an NFA that accepts all string over {0, 1} with a 1 in the third position from the end n Hint: the NFA stays in the start state until it guesses that it is three places from the end 0, 1 q 1 1 q 2 0, 1 Dr. Gary Weiss, January 27 2008 0, 1 q 3 q 4 35

Can we generate a DFA for this? n Yes, but it is more complicated and has 8 states See book Figure 1. 32 page 51 n Each state represents the last 3 symbols seen, where we assume we start with 000 n So, states 000, 001, 010, 011, …, 111 n What is the transition from 010 n n On a 1 we go to 101 n On a 0 we go to 100 Dr. Gary Weiss, January 27 2008 36

Formal Definition of Nondeterministic Finite Automata n Similar to DFA except includes ε and next state is not a state but a set of possible states n A nondeterministic finite automata is a 5 tuple (Q, , δ, q 0, F) where Q is a finite set called states n is a finite set called the alphabet n δ : Q x ε P(Q) is the transition function n q 0 Q is the start state n F Q is the set of accept states n Dr. Gary Weiss, January 27 2008 37

Example of Formal Definition of NFA 0, 1 q 1 n 1 q 2 NFA N 1 is (Q, , δ, q 1, F) n n Q = {q 1, q 2, q 3, q 4} = {0, 1} q 1 is the start state F = {q 4} 1 0, ε q 1 q 2 q 3 q 4 q 3 0 {q 1} {q 3} {q 4} Dr. Gary Weiss, January 27 2008 q 4 1 ε {q 1, q 2} {q 3} {q 4} 38

Equivalence of NFAs and DFAs n NFAs and DFAs recognize the same class of languages We say two machine are equivalent if they recognize the same language n NFAs have no more power than DFAs n n With respect to what can be expressed n But NFAs may make it much easier to describe a given language n Every NFA has an equivalent DFA Dr. Gary Weiss, January 27 2008 39

Proof of Equivalence of NFA & DFA n Proof idea Need to simulate an NFA with a DFA n With NFA’s, given an input we follow all possible branches and keep a finger on the state for each n That is what we need to keep track of– the states we would be in for each branch n If the NFA has k states then it has 2 k possible subsets n n Each subset corresponds to one of the possibilities that the DFA needs to remember n The DFA will Dr. have 2 k January states Gary Weiss, 27 2008 40

Proof by Construction n n Let N=(Q, , δ, q 0, F) be the NFA recognizing A Construct DFA M = (Q’, , δ’, q 0’, F’) n n n Lets do the easy ones first (skip δ’ for now) Q’ = P(Q) q 0’ ={q 0} F’ = {R Q’| R contains an accept state of N} Transition function n n The state R in M corresponds to a set of states in N When M reads symbol a in state R, it shows where a takes each state δ’(R, a) = Union of r R of δ(r, a) I ignore ε, but taking that into account does not fundamentally change the proof– we just need to keep Dr. Gary Weiss, January 27 2008 41 track of more states

Example: Convert an NFA to a DFA n See example 1. 41 on page 57 n n n For now don’t look at solution DFA The NFA has 3 states: Q = {1, 2, 3} What are the states in the DFA? n n { , {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}} What are the start states of the DFA? n n The start states of the NFA including those reachable by εmoves {1, 3} n n 3 is included because if we start in 1 we can immediately move to 3 What are the accept states? n {{1}, {1, 2}, {1, 3}, Dr. {1, 2, 3}} Gary Weiss, January 27 2008 42

Example: Convert an NFA to a DFA n Now lets work on some of the transitions n Let’s look at state 2 in NFA and complete the transitions for state 2 in the DFA n Where do we go from state 2 on an “a” and “b” n n So what state does {2} in DFA go to for a and b? n n Answer: on a to {2, 3} and {3} for b Now lets do state {3} n On “a” goes to {1, 3} and on b goes to n n On “a” to state 2 and 3 and on “b” to state 3 Why {1, 3}? Because first goes to 1 then ε permits a move back to 3! Now check DFA, Figure 1. 43 on page 58 n Any questions? Could you do it on a HW, exam, or quiz? Dr. Gary Weiss, January 27 2008 43

Closure under Regular Operations n We started this before and did it for Union only n Union much simpler using NFA Concatenation and Star much easier using NFA n Since DFAs equivalent to NFAs, we can now just use NFAs n In all cases, fewer states to keep track of, because we can act as if we can always “guess” correctly n Dr. Gary Weiss, January 27 2008 44

n Why do we care about closure? We need to look ahead A regular language is what a DFA/NFA accepts n We are now introducing regular operators and then will generate regular expressions from them (Ch 1. 3) n We will want to show that the language of regular expressions is equivalent to the language accepted by NFAs/DFAs (i. e. , a regular language) n How do we show this? n n Basic terms in regular expression can generated by a FA Dr. Gary Weiss, January 27 2008 45

Closure Under Union Given two regular languages A 1 and A 2 recognized by two NFAs N 1 and N 2, construct N to recognize A 1 A 2 n How do we construct N? Think! n Start by writing down N 1 and N 2. Now what? n Add a new start state and then have it take ε branches to the start states of N 1 and N 2 n Dr. Gary Weiss, January 27 2008 46

Closure under Concatenation Given two regular languages A 1 and A 2 recognized by two NFAs N 1 and N 2, construct N to recognize A 1 A 2 n How do we do this? n The complication is that we did not know when to switch from handling A 1 to A 2 since can loop thru an accept state n Solution with NFA: n n Connect every accept state in N 1 to every start state in N 2 using an ε transition n don’t remove transitions from accept state in N 1 back to N 1 Dr. Gary Weiss, January 27 2008 47

Closure under Concatenation II n Given: n n n N 1 = (Q 1, , δ 1, q 1, F 1) recognizes A 1 N 2 = (Q 2, , δ 2, q 2, F 2) recognizes A 2 Construct N=(Q 1 Q 2, , δ, q 1, F 2) so that it recognizes A 1 A 2 δ 1(q, a) δ(q, a) = δ 1(q, a) {q 2} δ 2(q, a) Dr. Gary Weiss, January 27 2008 q Q 1 and q F 1 and a ε q F 1 and a = ε q Q 2 48

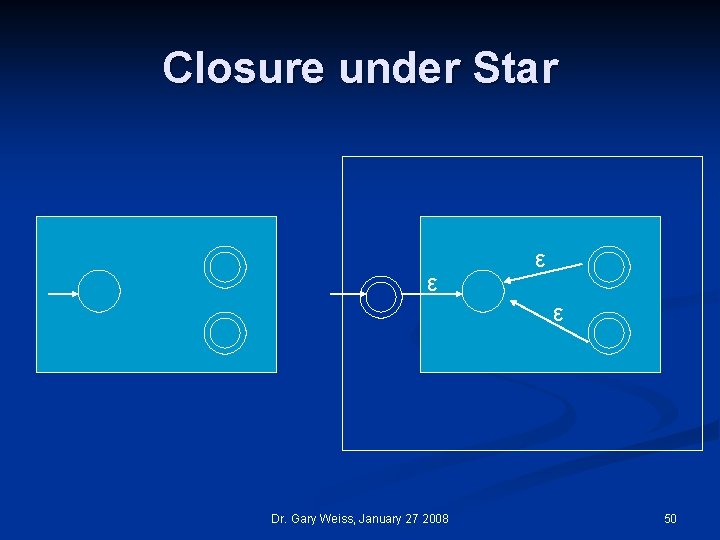
Closure under Star n We have a regular language A 1 and want to prove that A 1* is also regular n n Note (ab)* = { , abab, ababab, . . . } Proof by construction n n Take the NFA N 1 that recognizes A 1 and construct N from it that recognizes A 1* How do we do this? n n Add new ε-transition from accept states to start state Then make the start state the accept state so that is accepted n n This almost works, but not quite. What is the problem? n May have transition from intermediate state to start state and should not accept this. Solution: add a new start state with an ε-transition to the original start state and have ε-transitions from accept states 49 Dr. Gary Weiss, January 27 2008 to old start state

Closure under Star ε ε ε Dr. Gary Weiss, January 27 2008 50

Chapter 1. 3: Regular Expressions Dr. Gary Weiss, January 27 2008 51

Regular Expressions Based on the regular operators n Examples: n n (0 1)0* n. A 0 or 1 followed by any number of 0’s n Concatenation operator implied n What does (0 1)* mean? n All n possible strings of 0 and 1 Not 0* or 1* so does not require that commit to 0 or 1 before applying * operator n Assuming = {0, 1}, then equivalent to * Dr. Gary Weiss, January 27 2008 52

Definition of Regular Expression n R is a regular expression if R is 1. 2. 3. 4. 5. 6. n a, for some a in alphabet ε (R 1 R 2), where R 1 and R 2 are regular expressions (R 1*), where R 1 is a regular expression Note: n This is a recursive definition, common in computer science n n R 1 and R 2 always smaller than R, so no issue of infinite recursion means language does not include any strings and Dr. Gary Weiss, 27 2008 53 ε means it includes the. January empty string

Examples of Regular Expressions n 0*10* = n n *1 *= n n {w| w has at least one 1} 01 = n n {w| w contains a single 1} {01, 10} (0 ε)(1 ε) = n {ε, 0, 1, 01} Dr. Gary Weiss, January 27 2008 54

Equivalence of Regular Expressions and Finite Automata n Theorem: A language is regular if and only if some regular expression describes it n This has two directions so we need to prove: n If a language is described by a regular expression then it is regular n We will do both directions Dr. Gary Weiss, January 27 2008 55

Proof: Regular Expression Regular Language n Proof idea: Given a regular expression R describing a language L, we should … Show that some FA recognizes it n Use NFA since may be easier and equivalent to DFA n n How do we do this? n We will use definition of a regular expression and show that we can build a FA covering each step. n We n n will do quickly with two parts: Steps 1, 2 and 3 of definition (handle a, ε, and ) Steps 4, 5 and 6 (handle union, Dr. Gary Weiss, January 27 2008 concatenation, and star) 56

Proof Continued n For steps 1 -3 we construct the FA below. As a reminder: 1. 2. 3. a, for some a in alphabet ε a ε a Dr. Gary Weiss, January 27 2008 57

Proof Continued For steps 4 -6 (union, concatenation and star) we use the proofs we already constructed to show that FA are closed under union, concatenation, and star n So we are done with the proof in one direction n Now lets try an example n Dr. Gary Weiss, January 27 2008 58

Example: Regular Expression NFA n Convert (ab a)* to an NFA n See example 1. 56 page 68 n Lets n n describe the outline of what we need to do Handle ab a Handle (ab a)* n In the book they have states for ε-transitions. They seem unnecessary and may confuse you. They are in fact unnecessary in this case. n Now we need to do the proof in the other direction Dr. Gary Weiss, January 27 2008 59

Proof: Regular Language Regular Expression n A regular language is described by a DFA Need to show that can convert any DFA to a regular expression n The book goes through several pages (Lemma 1. 60 page 69 – 74) that does not really add much insight n n You can skip this. For the most part, if you understand the ideas for going in the previous direction, you also understand this direction. n But you should be able to handle an example … Dr. Gary Weiss, January 27 2008 60

Example: DFA Regular Expression This example is on page 75 n For the DFA below, what is the equivalent regular expression? n Answer: a*b(a b)* a 1 b 2 a, b Dr. Gary Weiss, January 27 2008 61

Chapter 1. 4: Nonregular Languages … and not the real fun begins Never has something so simple confused so many – Dr. Weiss Dr. Gary Weiss, January 27 2008 62

Non-Regular Languages n Do you think every language is regular? n n That would mean that every language can be described by a FA What might make a language non-regular? Think about the properties of a finite automata. Answer: finite memory n So a language is not regular if you need infinite memory n Dr. Gary Weiss, January 27 2008 63

Some Example Questions n Are the following languages regular? L 1 = {w| w has an equal number of 0’s and 1’s} n L 2 = {w| w has at least 100 1’s} n L 3 = {w| w is of the form 0 n 1 n, n≥ 0} n n First, write out some of the elements in each to ensure you have the terminology down L 1 = { , 01, 10, 1100, 0011, 0101, 1010, 0110, …} n L 2 = {(100 1’s), 0(100 1’s), 1(100 1’s), …} Dr. Gary Weiss, January 27 2008 n 64

Answers n Answers: n L 1 and L 3 are not, they require infinite memory n You n n cannot build a FA to recognize this language L 2 certainly is regular We will be studying only infinite languages Dr. Gary Weiss, January 27 2008 65

What is Wrong with This? n Question 1. 36 from the book asks Bn = {ak|where k is a multiple of n}, show for n≥ 1 Bn is regular. n How is this regular? How is this question different from the ones before? n n Each language has a specific value of n, so n is not a free variable as in other examples. However, k is a free variable. But the number of states is bounded by n, not k. Dr. Gary Weiss, January 27 2008 66

More on Regular Languages n Regular languages can be infinite but must be described using finite number of states Thus there are restrictions on the structure of regular languages n For a FA to generate an infinite set of string, clear there must be a ______ between some states n n loop n This leads to the (in)famous pumping lemma Dr. Gary Weiss, January 27 2008 67

Pumping Lemma for Regular Languages The pumping lemma states that all regular languages have a special property n If a language does not have this property it is not regular n So can use to prove a language non-regular n Note: the pumping lemma can hold and a language still not be regular. This is not usually highlighted. n Dr. Gary Weiss, January 27 2008 68

Pumping Lemma II n Pumping lemma property n n n Every string in a regular language L with length greater than the pumping length p can be “pumped” This means every string s L contains a section that can be repeated any number of times (via a loop) The string s can be written as xyz where 1. 2. 3. For each i ≥ 0, x yi z L |y| > 0, and |xy| ≤ p Dr. Gary Weiss, January 27 2008 69

Pumping Lemma Conditions n Condition 1: for each i ≥ 0, x yi z L n n Condition 2: |y| > 0 n n Without this condition, then there really would be no loop Condition 3: |xy| ≤ p n n This just says that there is a loop We don’t allow more states than the pumping length, since we want to bound the amount of memory All together, the conditions allow either x or z to be ε but not both n So loop need not be in the middle, which would be Dr. Gary Weiss, January 27 2008 70 limiting

Pumping Lemma Proof Idea n Set the pumping lemma length p to number of states of the FA If length of s ≤ pumping lemma trivially holds, so ignore these strings n Consider the states that the FA goes through for s n n Since there are only p states and length s > p, by pigeonhole property one state much be repeated n This means there is a cycle Dr. Gary Weiss, January 27 2008 71

Example 1 n Let B be the language {0 n 1 n| n≥ 0} (Ex 1. 73) n n Prove B is not regular We will use proof by contradiction. Assume B is regular. Now pick a string that will cause a problem. What string? Use the pumping length p in the string. Try 0 p 1 p n We need x yi z, let’s focus on y. n n n If y all 0’s or all 1’s, then if xyz L then xyyz L If y a mixture of 0 and 1, then 0’s and 1’s in s not completely separated But even simpler than this if use condition 3, which you should n Then y must be all 0’s and hence “pumping up” leads to a contradiction Dr. Gary Weiss, January 27 2008 72

Example 2 n Let C = {w|w has equal number of 0’s and 1’s} (Ex 1. 74) n Can you do this with finite memory? n n n No Prove C is not regular, using proof by contradiction Assume C is regular. Pick a problematic string. n n Let’s try 0 p 1 p If we pick y =01, can we pump it and have pumped string C? n n n Yes! Each time we pump (i. e. , loop) we add one 0 and 1. So works. Note however that pumped string not in 0 n 1 n, but that is okay since in C But cannot have x and z be ε n If |xy| < p then x and y can only be 0, since we start with 0 p n So y can. Dr. only 0 s and break equality Gary have Weiss, January 27 pumping 2008 73

Common-Sense Interpretation n FA can only use finite memory. If infinite strings, then the loop must handle this n If there are two parts that can generate infinite sequences, we must find a way to link them in the loop n If not, is not regular n Examples: 0 n 1 n equal numbers of 0 s and 1 s Dr. Gary Weiss, January 27 2008 74

Example 3 n Let F = {ww| w {0, 1}*} (Ex 1. 75) F = { , 00, 11, 0011, 0101, …} n Can you do this with finite memory? n n No n Use proof by contradiction. Pick s F that will be problematic p n 0 10 p 1 n n n If x and z could be ε, then easy (use y=0 p 1) Since |xy| < p, y must be all 0’s If we pump y, then only adding 0’s. That will be a problem. Since 0’s separated by 1 must be equal Dr. Gary Weiss, January 27 2008 75

Example 4 n Let D = {1 n 2| n ≥ 0} n n n D = { , 1, 111111111, …} Proof by contradiction Choose 1 p 2 n n Assume we have an xyz D What about xyyz? The # of 1’s differs from xyz by |y| n n n Since |xy| ≤ p then |y| ≤ p Thus xyyz has at most p more 1’s than xyz So if xyz has length ≤ p 2 then xyyz ≤ p 2 +p But p 2 + p < (p+1)2 = p 2 + 2 p + 1 Thus length of xyyz lies between consecutive perfect squares and hence xyyz D Dr. Gary Weiss, January 27 2008 76

Example 5 Let E = {0 i 1 j| i > j} p+1 p n Assume E is regular and let s = 0 1 n By condition 3, y must be all 0’s n n What can we say about xyyz? n Adding the extra y increases number of 0’s, which appears to be okay since i > j is okay n But we can pump down. What about xy 0 z = xz? n Since s has one more 0 than 1, removing at least one 0 leads to a contradiction. So not regular. Dr. Gary Weiss, January 27 2008 77

What you need to be able to do n n You should be able to handle examples like 1 -3. Example 5 is not really any more difficult, just one more thing to think about Example 4 was tough, so I won’t expect everyone to get an example like that You need to be able to handle the easy examples n n n On an exam, I would probably give you several problems that are minor variants of these examples Try to reason about the problem using “common sense” and then use that to drive your proof The homework problems will give you more practice Dr. Gary Weiss, January 27 2008 78