Computer Graphics Week 5 Shapes Scan Conversion 1
















- Slides: 18

Computer Graphics Week 5 – Shapes & Scan Conversion 1

Shapes and Scan Converting • The process by which an idealized shape, such as a line or a circle, is transformed into the correct "on" values for a group of pixels on the computer is called scan conversion and is also referred to as rasterizing. 2

1 -Line and linear shapes • The most popular line-drawing algorithm is the midpoint-line algorithm. • This algorithm takes the x- and y- coordinates of a line's endpoints as input and then calculates the x, y-coordinate pairs of all the pixels in between. 3

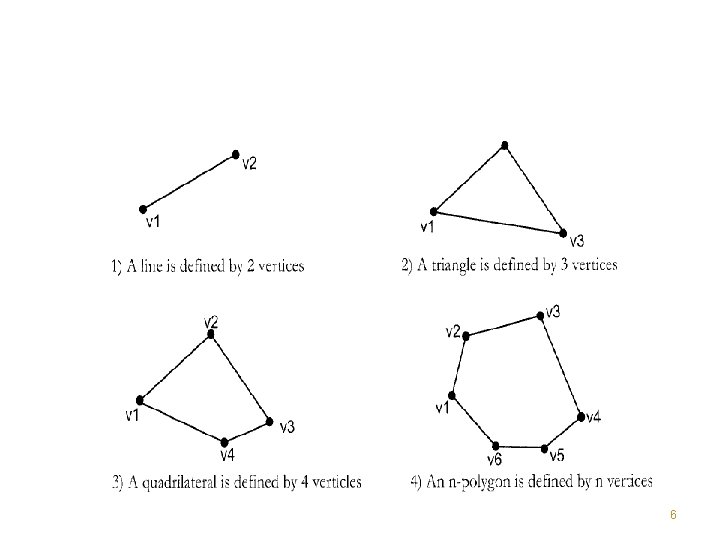
• Basic linear shapes such as triangles and polygons can be defined by a series of lines. • A polygon is defined by n number of vertices connected by lines, where n is the number of sides in the polygon. • A quadrilateral, which is a special case of a polygon is defined by four vertices, and a triangle is a polygon with three vertices 4

Relative drawing • void move. To(Gl. Point point){ curr. Point = point; } • void line. To(Gl. Point point) { gl. Begin(GL_LINES); gl. Vertex 2 f(curr. Point. x, curr. Point. y); gl. Vertex 2 f(point. x, point. y); //draw the line gl. End(); curr. Point= point; //update current point to new point gl. Flush(); } 5

6

• Open. GL geometric primitive types 7

2 -Circle and hyperbolic shapes • The basic mechanics for these algorithms are the same as for lines: figure out the pixels along the path of the shape, and turn the appropriate pixels on. • Interestingly, we can also draw a curved segment by approximating its shape using line segments. The smaller the segments, the closer the approximation. 8

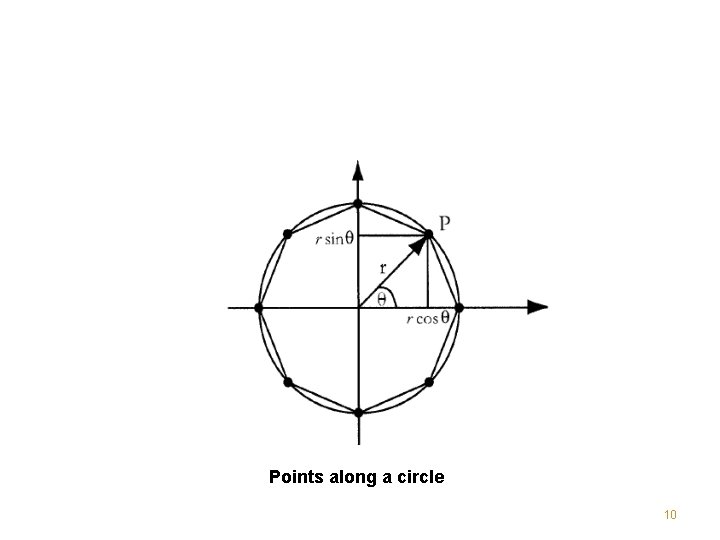
• For example, consider a circle. Recall from trigonometry that any point on a circle of radius r (and centered at the origin) has an x, y -coordinate pair that can be represented as a function of the angle theta the point makes with the axes 9

Points along a circle 10

11

2 D-Graphical objects • Poly. Lines- input from -file -interactive (using mouse) -computed (using relative drawing) • Curves -implicit form -parametric form 12

Drawing circle void draw. Circle (Point 2 center, float radius) { const int num. Verts = 50; // use larger value for a better circle ngon(num. Verts, center. get. X(), center. get. Y(), radius, 0); } 13

Drawing Arcs void draw. Arc(Gl. Point center, float radius, float start. Angle, float sweep) { // start. Angle and sweep are in degrees const int n = 30; // number of intermediate segments in arc float angle = start. Angle * 3. 14159265 / 180; // initial angle in radians float angle. Inc = sweep * 3. 14159265 /(180 * n); // angle increment Gl. Point point; point. x=center. x+ radius * cos(angle); point. y=center. y+ radius * sin(angle); move. To(point); for(int k = 1; k < n; k++, angle += angle. Inc){ point. x=center. x+ radius * cos(angle); point. y=center. y+ radius * sin(angle); line. To(point); } } 14

Curves • Implicit form F(x, y) = 0 • Straight line F(x, y)=(y-A 2)(B 1 –A 1)-(x-A 1)(B 2 –A 2) • Circle F(x, y)= x 2 +y 2 – R 2 • Inside – outside function F(x, y) < 0 inside the curve F(x, y) > 0 outside the curve 15

Curves • Parametric form – Current. Point = (x(t), y(t)) t ÎT • Straight line x(t) = A 1 +t(B 1 –A 1) y(t) = A 2 +t(B 2 –A 2) • Ellipse x(t) = A. cos(t) // A is width of ellipse y(t) = B. sin(t) // B is heigth of ellipse 16

Drawing ellipse void draw. Ellipse(Gl. Point center, float A, float B) { float cx=center. x; float cy=center. y; Gl. Point point; point. x=cx+A; point. y=cy; move. To(point); for (float t=0. 0; t<=TWOPI+0. 01; t+=TWOPI/100) { point. x=cx+A*cos(t); point. y=cy+B*sin(t); line. To(point); } gl. Flush(); } 17

Other conic sections Parabola F(x, y)= y 2 -4 ax x(t)=at 2 y(t)=2 at Hyperbola F(x, y)= (x/a)2 - (y/b)2 -1 x(t)=a/cos(t) y(t)=b. sin(t)/cos(t) 18