Computer Graphics UNIVERSITY OF NIZWA Allah says Say

Computer Graphics UNIVERSITY OF NIZWA Allah says Say, "Allah created cattle for you. In them you find warmth and benefit and from them you eat. In them there is beauty for you when you bring them home and when you take them out to the pasture. They bear your heavy loads to lands you could not have reached except with great effort. Surely, your Lord is Most Compassionate, Most Merciful. " Al-Qur'an, Surah an-Nahl, Verses 5 -7 1 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Lecture-2 Introduction to Computer Graphics Majed Bouchahma boumaged@unizwa. edu. om Computer Science Section Department of Physical and Mathematical Science

Computer Graphics UNIVERSITY OF NIZWA 2 D Graphics Primitives § Graphics drawing is based on basic geometric structures called graphics primitives § Points § Lines § Circles § Conic Sections § In this lecture we discuss how to draw the basic graphics primitives 3 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Drawing Points § Input specification § Coordinates (x, y) of the point § Color Specification § Procedure § Write the required color value to the corresponding position of the frame buffer § Color can be specified depending upon the graphics hardware interface e. g. RGB § For a black and white screen whenever a value of 1 is encountered the graphics system turns the corresponding pixel on black § Function Call § set. Pixel (x, y): To turn the pixel (x, y) on § get. Pixel (x, y): To get the pixel value for (x, y) © 2008, Fayyaz A. Afsar, DCIS, PIEAS. 4

Computer Graphics UNIVERSITY OF NIZWA Drawing Points… § Output 5 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

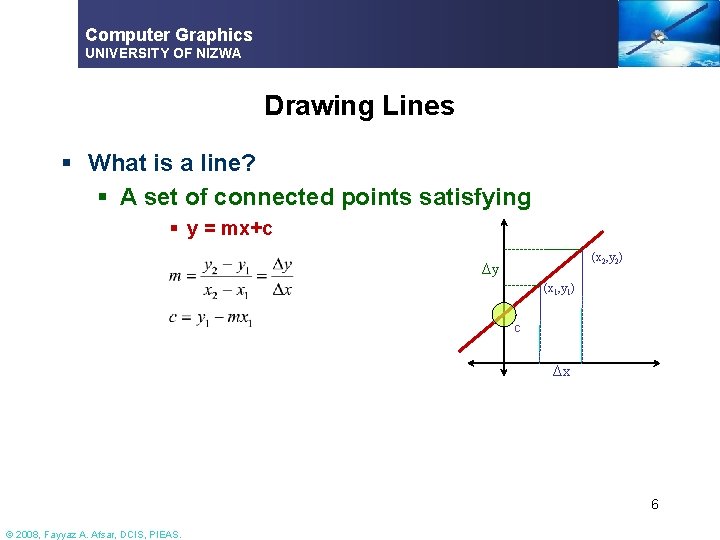
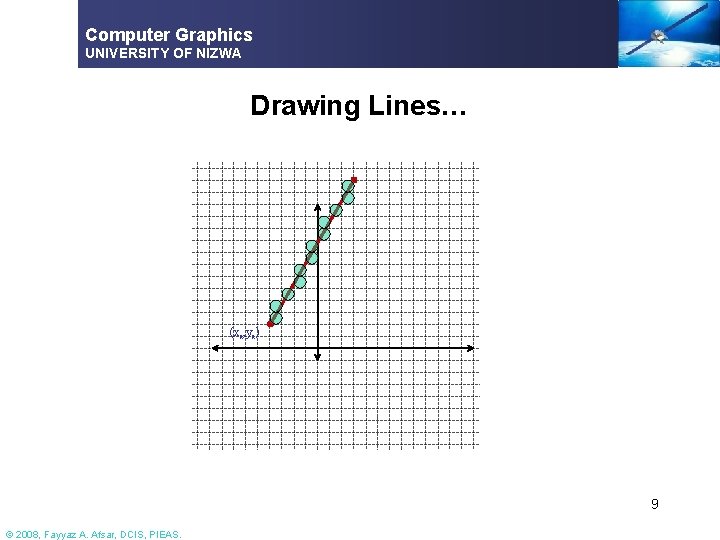
Computer Graphics UNIVERSITY OF NIZWA Drawing Lines § What is a line? § A set of connected points satisfying § y = mx+c (x 2, y 2) Δy (x 1, y 1) c Δx 6 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

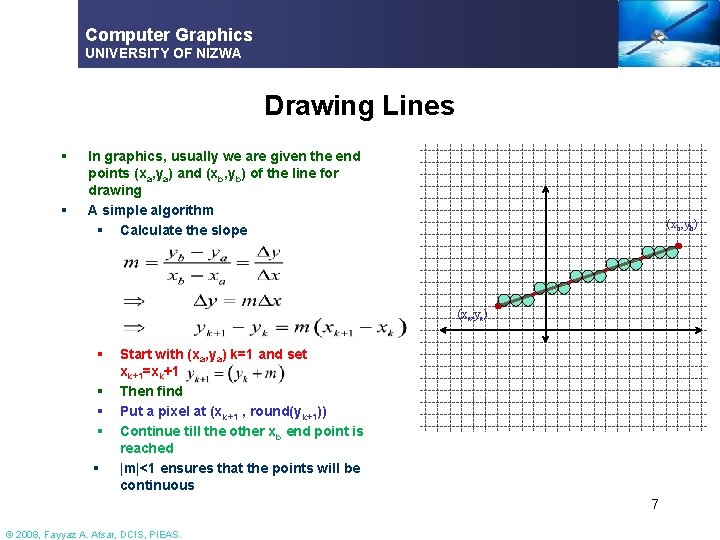
Computer Graphics UNIVERSITY OF NIZWA Drawing Lines § § In graphics, usually we are given the end points (xa, ya) and (xb, yb) of the line for drawing A simple algorithm § Calculate the slope (xb, yb) (xa, ya) § § § Start with (xa, ya) k=1 and set xk+1=xk+1 Then find Put a pixel at (xk+1 , round(yk+1)) Continue till the other xb end point is reached |m|<1 ensures that the points will be continuous 7 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

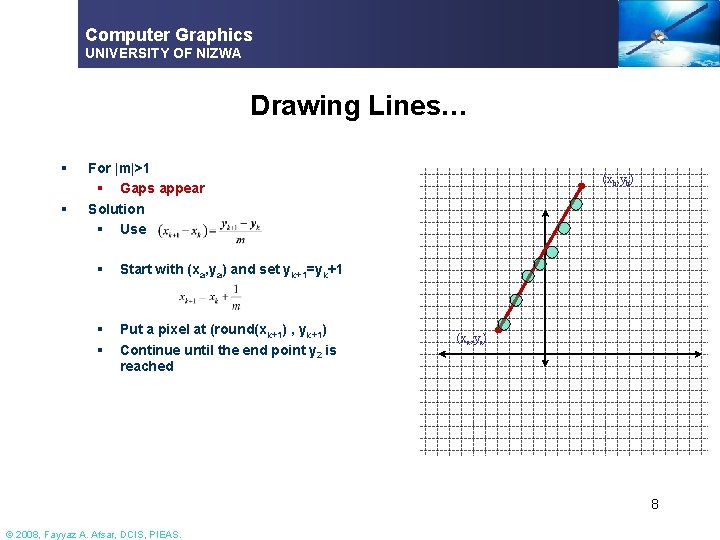
Computer Graphics UNIVERSITY OF NIZWA Drawing Lines… § § For |m|>1 § Gaps appear Solution § Use § Start with (xa, ya) and set yk+1=yk+1 § § Put a pixel at (round(xk+1) , yk+1) Continue until the end point y 2 is reached (xb, yb) (xa, ya) 8 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Drawing Lines… (xa, ya) 9 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Drawing Lines… § This procedure is called the DDA Algorithm § Digital Differential Analyzer void line. DDA(int xa, int ya, int xb, int yb) { int dx=xb-xa, dy=yb-ya, steps, k; float x. Increment, y. Increment, x=xa, y=ya; if ( abs(dx) > abs(dy) ) steps = abs (dx); else steps = abs (dy); x. Increment = dx / (float) steps; y. Increment = dy / (float) steps; set. Pixel (round (x), round (y)); for (k=0; k<steps; k++){ x += x. Increment; y += y. Increment; set. Pixel (round (x), round (y)); } } 10 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

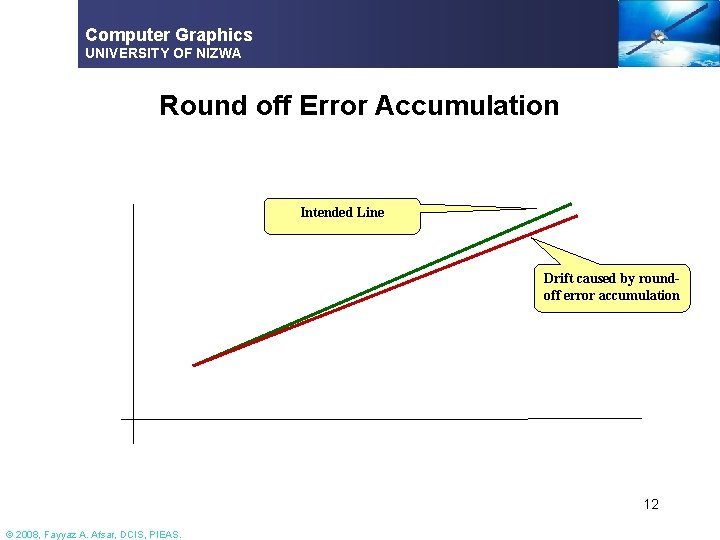
Computer Graphics UNIVERSITY OF NIZWA Line Drawing: DDA § Characteristics § Efficiency § Better than direct line drawing y=mx+c § Eliminates Multiplication § But uses rounding off which is an expensive operation § Uses floating point operations § Round off errors can cause the line to drift away from the true line segment § Especially for long lines § Can be a problem for systems with low precision 11 numeric representation © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Round off Error Accumulation Intended Line Drift caused by roundoff error accumulation 12 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA The Bresenham Line Algorithm § The Bresenham algorithm is another incremental scan conversion algorithm § The big advantage of this algorithm is that it uses only integer calculations Jack Bresenham worked for 27 years at IBM before entering academia. Bresenham developed his famous algorithms at IBM in the early 1960 s

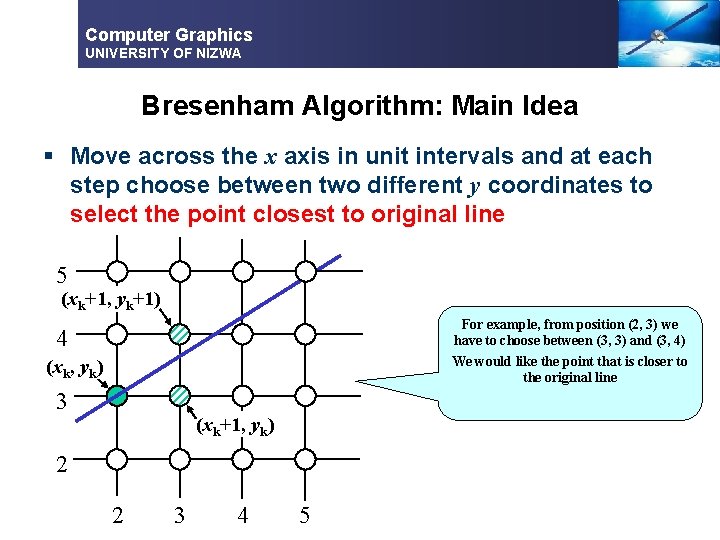
Computer Graphics UNIVERSITY OF NIZWA Bresenham Algorithm: Main Idea § Move across the x axis in unit intervals and at each step choose between two different y coordinates to select the point closest to original line 5 (xk+1, yk+1) For example, from position (2, 3) we have to choose between (3, 3) and (3, 4) We would like the point that is closer to the original line 4 (xk, yk) 3 (xk+1, yk) 2 2 3 4 5

Computer Graphics UNIVERSITY OF NIZWA Deriving The Bresenham Line Algorithm § At sample position xk+1 the vertical separations from the mathematical line are yk+1 labelled dupper and dlower § The y coordinate on the mathematical line at xk+1 is: y yk dupper dlower xk+1 Our assumption here is that the line has a positive slope less than one

Computer Graphics UNIVERSITY OF NIZWA Deriving The Bresenham Line Algorithm (cont…) § So, dupper and dlower are given as follows: § and: § We can use these to make a simple decision about which pixel is closer to the mathematical line

Computer Graphics UNIVERSITY OF NIZWA Deriving The Bresenham Line Algorithm (cont…) § This simple decision is based on the difference between the two pixel positions: § Let’s substitute m with ∆y/∆x where ∆x and ∆y are the differences between the end-points: Since in our case Δx is positive therefore this term has the same sign as dlower-dupper Constant terms collected in ‘c’

Computer Graphics UNIVERSITY OF NIZWA Deriving The Bresenham Line Algorithm (cont…) § So, a decision parameter pk for the kth step along a line is given by: § The sign of the decision parameter pk is the same as that of dlower – dupper § If pk is negative, then we choose the lower pixel, otherwise we choose the upper pixel

Computer Graphics UNIVERSITY OF NIZWA Deriving The Bresenham Line Algorithm (cont…) § Remember coordinate changes occur along the x axis in unit steps so we can do everything with integer calculations § At step k+1 the decision parameter is given as: § Subtracting pk from this we get:

Computer Graphics UNIVERSITY OF NIZWA Deriving The Bresenham Line Algorithm (cont…) § But, xk+1 is the same as xk+1 so: § where yk+1 - yk is either 0 or 1 depending on the sign of pk § The first decision parameter p 0 is evaluated at (x 0, y 0) is given as:

Computer Graphics UNIVERSITY OF NIZWA The Bresenham Line Algorithm BRESENHAM’S LINE DRAWING ALGORITHM (for |m| < 1. 0) 1. 2. 3. 4. Input the two line end-points, storing the left end-point in (x 0, y 0) Plot the point (x 0, y 0) Find: At each xk along the line, starting at k = 0, perform the following test. If pk < 0, the next point to plot is (xk+1, yk) and: Otherwise, the next point to plot is (xk+1, yk+1) and: 5. Repeat step 4 (Δx – 1) times

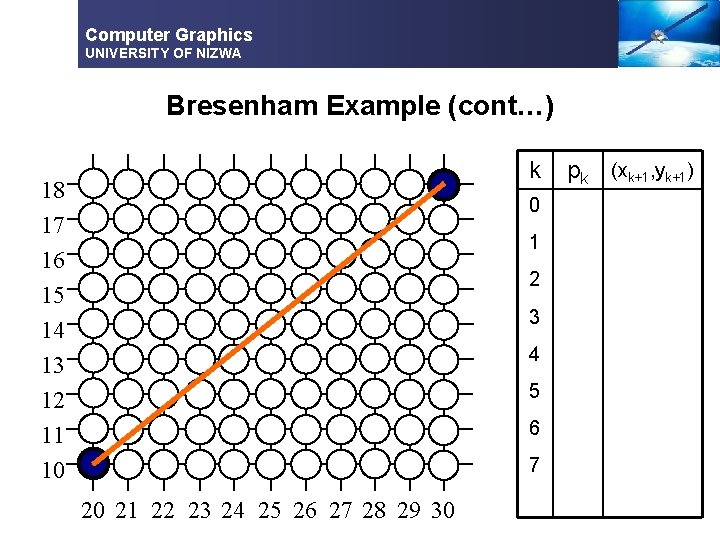
Computer Graphics UNIVERSITY OF NIZWA Bresenham Example § Let’s have a go at this § Let’s plot the line from (20, 10) to (30, 18) § First off calculate all of the constants: § Δx: 10 § Δy: 8 § 2Δy: 16 § 2Δy - 2Δx: -4 § Calculate the initial decision parameter p 0: § p 0 = 2Δy – Δx = 6

Computer Graphics UNIVERSITY OF NIZWA Bresenham Example (cont…) k 18 17 16 15 14 13 12 11 10 0 1 2 3 4 5 6 7 20 21 22 23 24 25 26 27 28 29 30 pk (xk+1, yk+1)

Computer Graphics UNIVERSITY OF NIZWA Bresenham Exercise § Go through the steps of the Bresenham line drawing algorithm for a line going from (21, 12) to (29, 16)

Computer Graphics UNIVERSITY OF NIZWA Generalization of the Bresenham Line Drawing Algorithm § For lines with slopes greater than 1 § Inter-change the roles of the x and y directions § Take a unit step in y direction and calculate x values nearest to the line path § For lines with negative slopes § Procedure is generally similar except that now one coordinate decreases as the other increases § Vertical, Horizontal and Diagonal lines § Can be drawn as special cases without processing by the line plotting method § Interchange of the starting and ending points can be checked 25 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Characteristics of Bresenham Line Drawing Algorithm § Uses only integer calculations § More efficient § Paves the way for making more complex curves based upon a similar logic § Take the screen pixel closest to the original curve 26 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Assignment-1 § Write pseudo-codes of Bresenham Line Drawing Algorithms for lines of Arbitrary slopes § Implement DDA and Bresenham Line Drawing Algorithms using Open. GL to draw lines of Arbitrary slopes given the starting and end points § Assignment Due: 29 th October 2009 in lab § Evaluation: Via viva and code structure § Marks (% of total marks): 3% 27 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Drawing Circles § A Circle is the set of points that are all at a given distance r (called radius) from a center point (xc, yc) § The equation for a circle is: § The circle is a frequently used component in pictures and graphics 28 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Drawing Circles… § A circle can be drawn by using the following equation by moving in unit steps from xc-r to xc+r and calculating the corresponding y value at each position 29 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

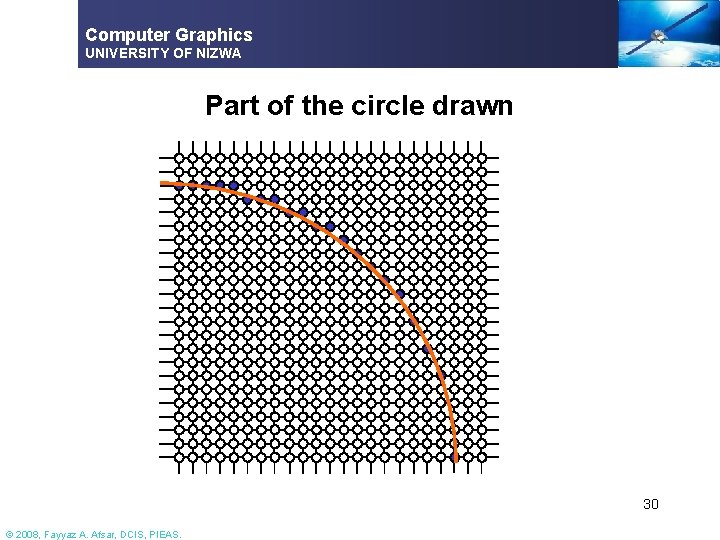
Computer Graphics UNIVERSITY OF NIZWA Part of the circle drawn 30 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Drawing a Circle… § Problems with this approach § Computations § Spacing between points is not uniform § Reason § Absolute value of the slope exceeds 1 § Solution-1 § Switch the roles of x and y when the absolute value of slope exceeds 1 § Increment y by one unit and calculate corresponding x § Still computationally complex 31 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Drawing a circle… § Problems… § Solution-2 § Use parametric polar form of the circle § Start with initial angle equal to zero and increment the angle to get and then plot the next point § The increment in the angle should be small (1/r) to ensure a continuous boundary or if a large step is used then the points can be connected by straight lines to approximate a circular boundary 32 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Drawing a circle… § Problems… § Solution-2… § The increment of 1/r ensures continuity of the points § A similar relation can be obtained for yk and as therefore continuity is ensured 33 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

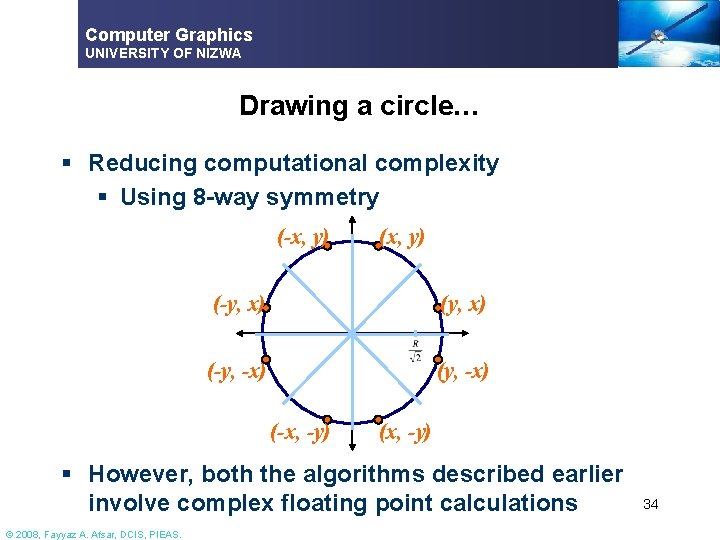
Computer Graphics UNIVERSITY OF NIZWA Drawing a circle… § Reducing computational complexity § Using 8 -way symmetry (-x, y) (-y, x) (-y, -x) (-x, -y) (x, -y) § However, both the algorithms described earlier involve complex floating point calculations © 2008, Fayyaz A. Afsar, DCIS, PIEAS. 34

Computer Graphics UNIVERSITY OF NIZWA Drawing a circle: Midpoint Circle Algorithm § The midpoint circle algorithm has been developed and patented by J. Bresenham § Charcteristics of MPCA § Incremental in nature § Uses a decision parameter to find the pixel closest to the circumference of the original circle § Uses (almost all) integer operations § Uses 8 -way symmetry to reduce computations 35 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

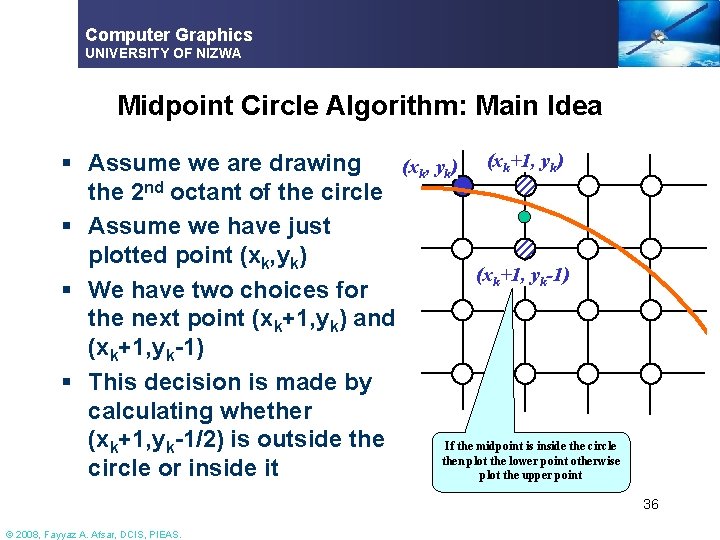
Computer Graphics UNIVERSITY OF NIZWA Midpoint Circle Algorithm: Main Idea § Assume we are drawing (xk, yk) (xk+1, yk) the 2 nd octant of the circle § Assume we have just plotted point (xk, yk) (xk+1, yk-1) § We have two choices for the next point (xk+1, yk) and (xk+1, yk-1) § This decision is made by calculating whether (xk+1, yk-1/2) is outside the If the midpoint is inside the circle then plot the lower point otherwise circle or inside it plot the upper point 36 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Midpoint Circle Algorithm: Main Idea… § This can be done by using the circle function based on the equation of the circle § Thus our decision parameter is 37 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Midpoint Circle Algorithm… § We decide yk+1 on the basis of pk § pk+1 is given by, 38 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Midpoint Circle Algorithm… 39 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Midpoint Circle Algorithm… § The initial decision parameter can be obtained by evaluating the circle function at (x 0, y 0 -1/2)=(0, r 1/2) If the redius is an integer then 5/4 can be rounded off to 1 to ensure integer operations © 2008, Fayyaz A. Afsar, DCIS, PIEAS. 40

Computer Graphics UNIVERSITY OF NIZWA The Mid-Point Circle Algorithm… 1. Input radius r and circle centre (xc, yc), then set the coordinates for the first point on the circumference of a circle centred on the origin as: 2. Calculate the initial value of the decision parameter as: 3. Starting with k = 0 at each position xk, perform the following test. If pk < 0, the next point along the circle centred on (0, 0) is (xk+1, yk) and:

Computer Graphics UNIVERSITY OF NIZWA The Mid-Point Circle Algorithm… § Otherwise the next point along the circle is (xk+1, yk-1) and: 4. 5. Determine symmetry points in the other seven octants Move each calculated pixel position (x, y) onto the circular path centred at (xc, yc) to plot the coordinate values: 6. Repeat steps 3 to 5 until x >= y

Computer Graphics UNIVERSITY OF NIZWA Mid-Point Circle Algorithm Example § To see the mid-point circle algorithm in action lets use it to draw a circle centred at (0, 0) with radius 10

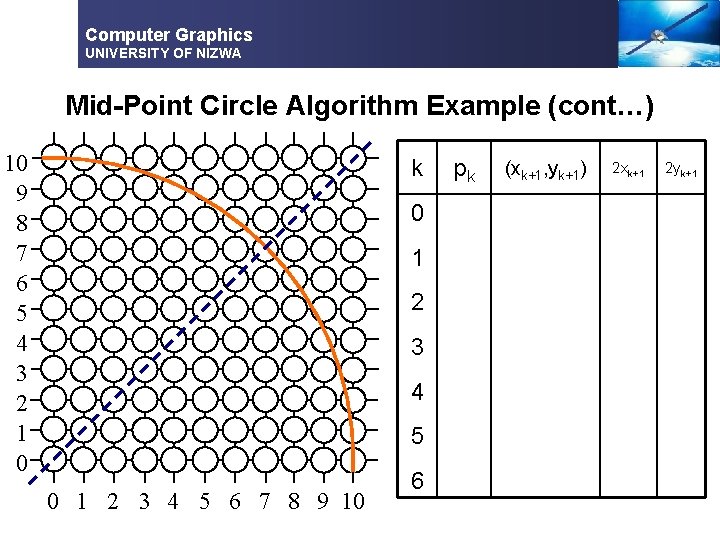
Computer Graphics UNIVERSITY OF NIZWA Mid-Point Circle Algorithm Example (cont…) 10 9 8 7 6 5 4 3 2 1 0 k 0 1 2 3 4 5 6 7 8 9 10 6 pk (xk+1, yk+1) 2 xk+1 2 yk+1

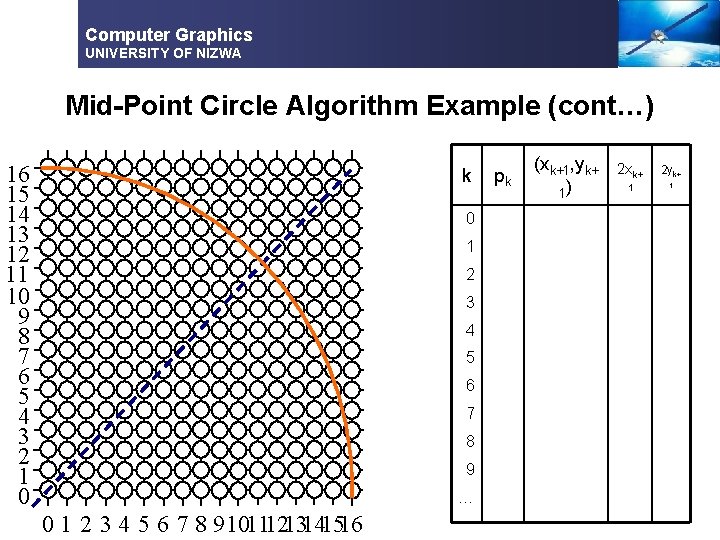
Computer Graphics UNIVERSITY OF NIZWA Mid-Point Circle Algorithm Exercise § Use the mid-point circle algorithm to draw the circle centred at (0, 0) with radius 15

Computer Graphics UNIVERSITY OF NIZWA Mid-Point Circle Algorithm Example (cont…) 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 k 0 1 2 3 4 5 6 7 8 9 … 0 1 2 3 4 5 6 7 8 910111213141516 pk (xk+1, yk+ 1) 2 xk+ 2 yk+ 1 1

Computer Graphics UNIVERSITY OF NIZWA Generalized Midpoint Algorithm for Drawing Curves § The midpoint algorithm can be generalized to draw complex curves if the equation of the curve is known § Develop the curve function f(x, y) which indicates whether the point (x, y) is above, below or on the curve § Use this function to establish a decision parameter pk which decides which of the two selected points will be plotted by using the mid point of the selected points as a parameter to the curve function § The options may be (top or bottom) or (left or right) depending upon the direction of unit increment on the basis of slope § Develop a recurrence relation for pk+1 § Apply unit increment along one axis and evaluate the value of the other on the basis of decision parameter to draw the curve 47 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Drawing an Ellipse using Midpoint algorithm § An ellipse is described by the equation d 2 y) , x P( d 1 © 2008, Fayyaz A. Afsar, DCIS, PIEAS. F 1( y 1) , x 1 y 2) , x 2 F 2( 48

Computer Graphics UNIVERSITY OF NIZWA Drawing an Ellipse using Midpoint algorithm § If the major and minor axis of the ellipse are parallel to x and y axes then the equation can be written as ry rx C(xc, yc) 49 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Symmetry in an ellipse § With its center at origin the symmetry points can be described as (-x, y) (x, y) ry rx C(0, 0) (-x, -y) (x, -y) § We can minimize drawing computation by drawing only one quadrant of an ellipse with its center at origin and then using symmetry to complete the curve § The final ellipse can then be rotated and translated to any desired position 50 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Midpoint algorithm for drawing an ellipse § Consider an ellipse with its center at the origin and rx<ry § The part of the ellipse in the 1 st quadrant can be drawn by § Taking increment in x-direction where the magnitude of the slope is less than 1 and finding the corresponding pixel y-values nearest to the original curve § Taking increment in y-direction where the magnitude of the slope is greater than 1 and finding the corresponding pixel x-values nearest to the original curve 51 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Midpoint algorithm for drawing an ellipse 0≥m>-1 Region-1 m=-1 -1>m>-∞ Region-2 52 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Midpoint algorithm for drawing an ellipse… § To draw the ellipse in region 1, we will first assume that we have placed a pixel (xk, yk) and the next pixel to be drawn is (xk+1, yk+1) for which yk+1 can be yk or yk-1 and xk+1=xk+1 § yk+1 depends upon whether the midpoint (xk+1, yk-1/2) lies above or below the original curve © 2008, Fayyaz A. Afsar, DCIS, PIEAS. yk yk+1 Midpoint (xk+1, yk-1/2) xk xk+1 53

Computer Graphics UNIVERSITY OF NIZWA Midpoint algorithm for drawing an ellipse… § The decision function being used to detect whether (x, y) is above the curve or below it is given by: § The decision parameter for Region-1 can be calculated as 54 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Midpoint algorithm for drawing an ellipse… § Now 55 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Midpoint algorithm for drawing an ellipse… § At (0, ry) the two terms (2 ry 2 x and 2 rx 2 y) can be obtained as § As x and y are incremented, the updated values of these terms can be obtained by adding 2 ry 2 to the first term and subtracting 2 ry 2 from the second term § Thus the evaluation of these terms can be done through only multiplications and divisions 56 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Midpoint algorithm for drawing an ellipse… § For p 10 57 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA Midpoint algorithm for drawing an ellipse… § To Do: § See and complete the proof for Region 2 along with the pseudo code for drawing the complete ellipse 58 © 2008, Fayyaz A. Afsar, DCIS, PIEAS.

Computer Graphics UNIVERSITY OF NIZWA End of Lecture-2 To choose time is to save time. Francis Bacon (1561– 1626), English philosopher, lawyer, and statesman. Essays "Of Dispatch" (1625)