COMPUTER GRAPHICS MATRICES CO 2409 Weeks 67 LECTURE

COMPUTER GRAPHICS MATRICES CO 2409 Weeks 67

LECTURE CONTENTS 1. Meshes/Models & World/Model Space 2. Matrices for Positioning 3. Matrix Definitions 4. Matrix Arithmetic

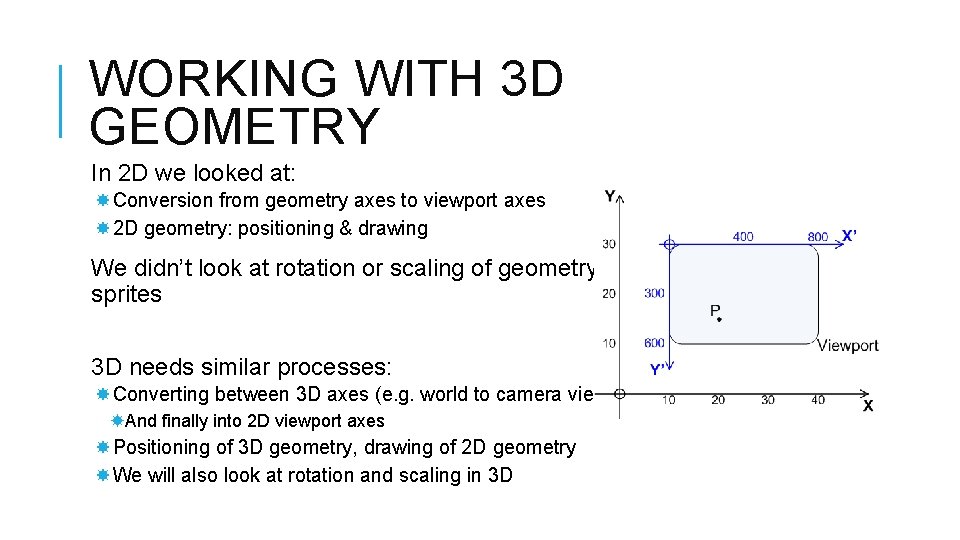
WORKING WITH 3 D GEOMETRY In 2 D we looked at: Conversion from geometry axes to viewport axes 2 D geometry: positioning & drawing We didn’t look at rotation or scaling of geometry / sprites 3 D needs similar processes: Converting between 3 D axes (e. g. world to camera view) And finally into 2 D viewport axes Positioning of 3 D geometry, drawing of 2 D geometry We will also look at rotation and scaling in 3 D

MESHES AND MODELS A mesh defines some 3 D geometry We define a model as a single instance of a mesh in a 3 D scene Like a sprite is an instance of a bitmap in a 2 D scene Several models may use the same mesh in the scene Like several sprites using the same bitmap Each model can be positioned differently Position, rotation and scaling Example of two models of a square mesh: 1 mesh, 2 models

WORLD / MODEL SPACE Define our 3 D scene using fixed axes XW YW & ZW A global view of the world and everything in it This is called world space or the world coordinate system The axes are the world axes (in red) An arbitrarily positioned model has: A position P and local axes, X, Y & Z The local axes are its own rightward, upward & forward directions This is the model’s local space or local coordinate system Also called model space Compare to the two overlaid sets of axes we saw in

MODEL POSITIONING So the position and rotation of a 3 D model can be specified by defining its local space: Position: a 3 D vertex P Rotation: three 3 D vectors – Right, Up and Forward (X, Y & Z) What about scaling? The length of vectors X, Y & Z define the scaling in that axis 1. 0 = unscaled, 2. 0 = double size etc. Effectively scaling local space

MATRICES FOR POSITIONING We can put these 4 elements into a 4 x 3 matrix: (RX, RY, RZ) is the model’s rightward direction, which is its local X axis (UX, UY, UZ) is the up direction (local Y axis) (FX, FY, FZ) the forward direction (local Z axis) These are 3 D vectors (PX, PY, PZ) is the model’s position All defined in world space units Example on later slide Or we can use a 3 x 4 matrix Put everything in columns rather than rows Direct. X docs use rows, math books and Open. GL docs use columns. We will use rows. or

ALTERNATIVE WRITTEN FORM Here the local X, Y & Z axes are written as R, U and F for right, up and forward: Easier to understand Can also use letters X, Y and Z to give this equivalent form: I sometimes use this form too Maths texts may present this matrix with different letters again This is just presentation, the matrix always has the same basic layout

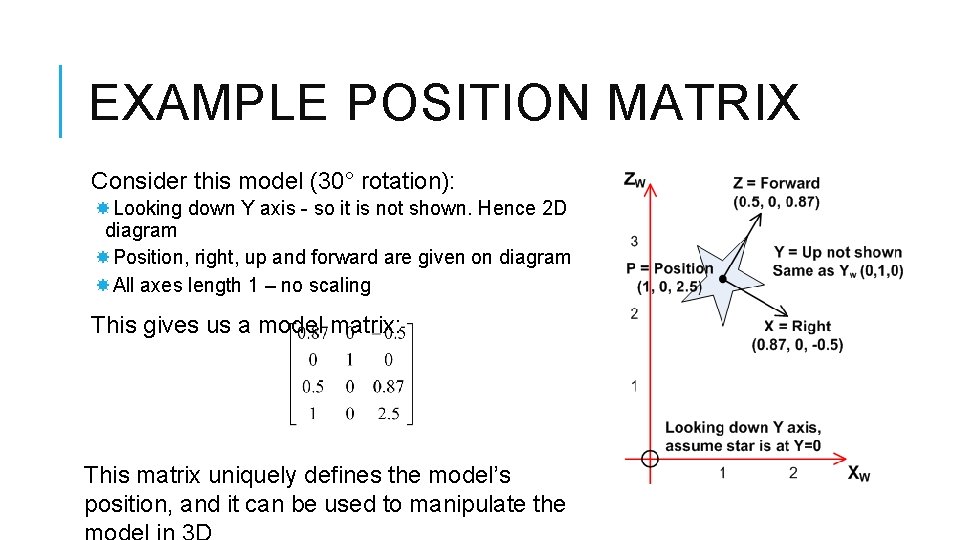
EXAMPLE POSITION MATRIX Consider this model (30° rotation): Looking down Y axis - so it is not shown. Hence 2 D diagram Position, right, up and forward are given on diagram All axes length 1 – no scaling This gives us a model matrix: This matrix uniquely defines the model’s position, and it can be used to manipulate the

MATRIX DEFINITION A matrix (plural matrices) is a rectangular table of numbers: Matrices can have any number of rows and columns. A matrix with m rows and n columns is called an m by n matrix The above matrices are 3 x 3 and 2 x 4 The value at the i-th row and j-th column is denoted Aij In the example above: M 23 = 5 and N 14 = 2

SIMPLE MATRICES A 1 xn or nx 1 matrix can represent a set of coordinates E. g. a vector or vertex/point: A square matrix is one with a equal number of rows and columns, e. g. M from last slide A 1 x 1 matrix is simply a number

SIMPLE MATRIX ARITHMETIC Addition - equal size matrices can be added: Subtraction – similar to addition: Multiplication by a scalar:

MATRIX MULTIPLICATION We can multiply two matrices R = AB if: Number of columns in A = number of rows in B Result has same number of rows as A and columns as B So if multiplying 2 x 3 & 3 x 4 matrices, we get 2 x 4 matrix result Values in the result matrix are given by this formula: Rij = Ai 1 B 1 j + Ai 2 B 2 j +. . . + Ain. Bnj The value in row i and column j of R is the dot product of i-th row of A & j-th column of B

MATRIX MULTIPLICATION PROPERTIES Matrix multiplication is associative: (AB)C = A(BC) And distributive: (A + B)C = AC + BC, C(A + B) = CA + CB This is the same as scalars But matrix multiplication is not commutative: AB ≠ BA (in general) Very important for transformations later The order in which you multiply matrices has an effect on the result matrix

SQUARE MATRICES Square matrices can always be multiplied The result is a square matrix of the same size A square matrix with only 1’s down the diagonal has special properties: Such a matrix does not change other matrices under multiplication This is called the identity matrix Or the unit matrix (similarity with the number 1)

TRANSFORMATIONS (3 X 3) A vector or vertex can be represented as a 1 x 3 matrix: Multiply by a 3 x 3 matrix we get another 1 x 3 matrix: The vertex/vector changes (transforms) into a new one This square matrix is a transformation matrix or simply a transform Almost all the vertex processing needed for 3 D graphics can be performed with transformation matrices However, 3 x 3 matrices cannot perform some transformations we need (movement)

TRANSFORMATIONS (4 X 4) So we add another element (p) to the vector / vertex to get a 1 x 4 matrix: Then multiply by a 4 x 4 matrix to perform a transformation Take the right column from the unit matrix (see earlier slide) Note that the transformation leaves the extra element p unchanged This kind of 4 x 4 transformation matrix can perform all transformations we need for 3 D

TH 4 THE ELEMENT / MESH TRANSFORMS The 4 th element p specifies if the x, y & z values represent a vertex (point) or a vector 1 = vertex, 0 = vector Previously we couldn’t distinguish between them (both just x, y, z) For example: If we transform all vertices & normals in a mesh then the entire mesh will be transformed Recall that normals are just vectors

ADVANCED NOTE: HOMOGENOUS COORDINATES A coordinate in 3 D is just an x, y, z point. E. g. (10, 15, -5) The 4 element coordinates from the last slide are called homogenous 3 D coordinates They have x, y, z values plus an extra 4 th value To convert a homogenous coordinate to a point, you divide the x, y and z by the 4 th element. The 4 th element is only used like this in creating perspective (see later), and at all other times it will only be 1 or 0 in our work If the 4 th element is 1, dividing by 1 leaves the x, y, z the same If the 4 th element is 0, you can’t divide by 0 indicating that this is not a point, but a vector This is only used for advanced work, but is mentioned here since some texts

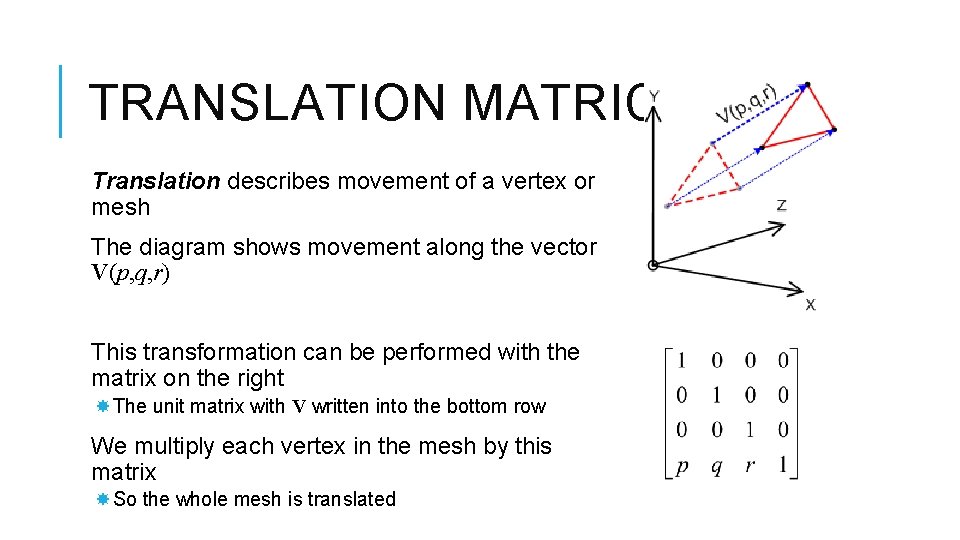
TRANSLATION MATRICES Translation describes movement of a vertex or mesh The diagram shows movement along the vector V(p, q, r) This transformation can be performed with the matrix on the right The unit matrix with V written into the bottom row We multiply each vertex in the mesh by this matrix So the whole mesh is translated

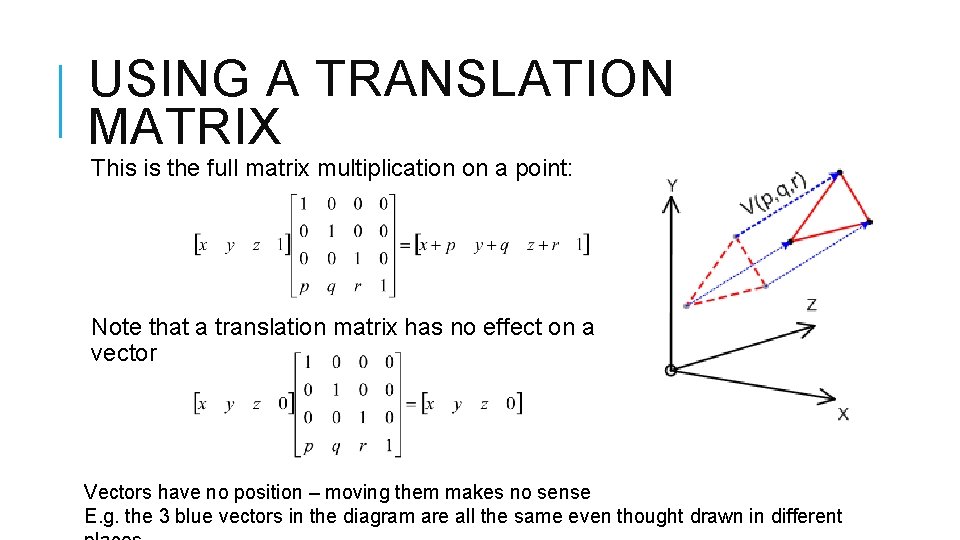
USING A TRANSLATION MATRIX This is the full matrix multiplication on a point: Note that a translation matrix has no effect on a vector Vectors have no position – moving them makes no sense E. g. the 3 blue vectors in the diagram are all the same even thought drawn in different

ROTATION MATRICES A rotation matrix rotates a vertex or mesh around an axis Most often around the X, Y or Z axis Could be the world axes or the local axes of a mesh (will see this later) The diagram shows a rotation around the Z-axis A point or vector can be made to do a Z rotation by multiplying it with the matrix on the right: cos and sin appear since we are working with a circle

USING A ROTATION MATRIX The rotate-Z matrix is used like this: (not showing full formula for result x & y for simplicity) Several important notes: Z values don’t change when rotating around the Z axis The rotation is around the origin Not around the centre of the triangle Vectors are affected by rotation For example, the edges of the triangle are vectors - notice they are rotated too

OTHER ROTATION MATRICES Can rotate around the X & Y axes using similar matrices The three basic rotation matrices are: Note how the row (& column) of the axis of rotation is unchanged in each version

SCALING MATRICES A scaling matrix scales geometry around the origin The matrix is like the unit matrix with the scaling value on the diagonal: Note: Scaling is centred on the origin Note: Vectors are affected by scaling We can form a non-regular scaling matrix (different scaling in X, Y & Z):

COMBINING TRANSFORMATIONS We can combine the effect transformations by multiplying their matrices together E. g. A scale followed by a translation: The resulting matrix can then be used as a combined transformation for vertices / vectors:

ORDER OF TRANSFORMATIONS The order of transformations is important Same example as the last slide reversed: translation followed by a scale: The result matrix is different The translation has been scaled, as it occurred first Recall that matrices are not commutative I. e. AB ≠ BA in general So it is very important to consider the order of transformations before multiplying

CREATING COMBINED TRANSFORMATIONS Say we want a scaling matrix that will scale around a given point rather than the origin We can do this with three basic transforms: Translate the point to the origin Scale (around the origin) Translate the origin back to the point The result matrix is potentially useful Would have been difficult to guess