Computer Graphics Lezione 7 rasterizzazione la fabbrica dei

Computer Graphics Lezione 7: rasterizzazione la fabbrica dei frammenti Università dell’Insubria Facoltà di Scienze MFN di Varese Corso di Laurea in Informatica Anno Accademico 2005/06 Marco Tarini

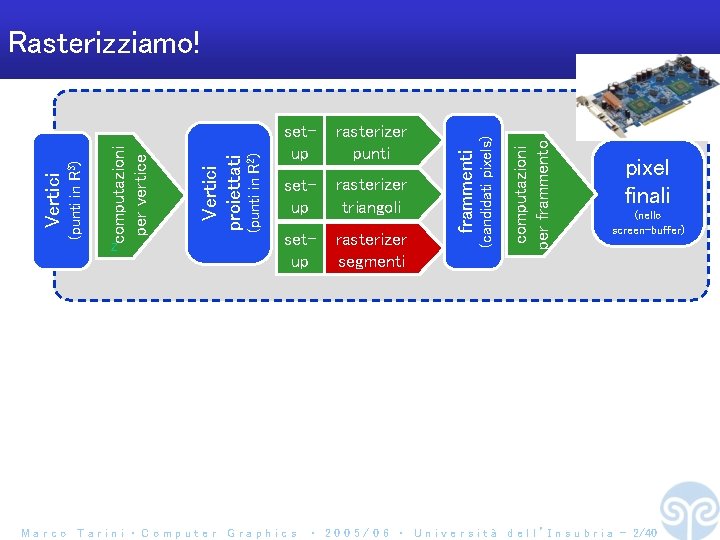
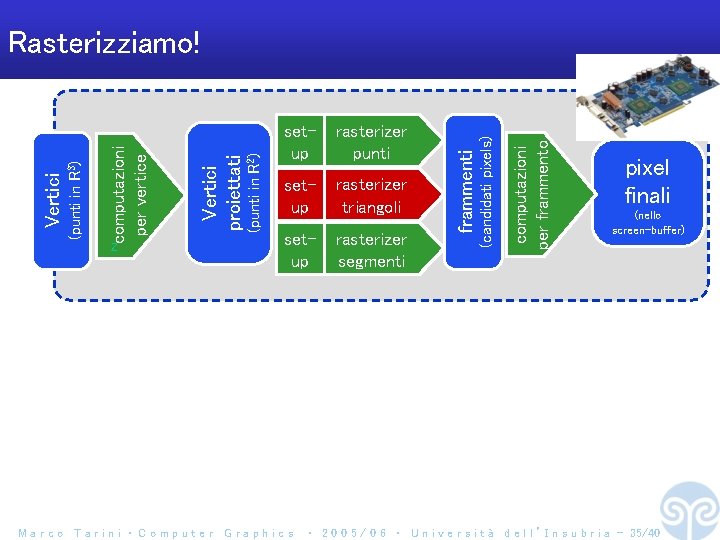
setup rasterizer triangoli setup rasterizer segmenti Marco Tarini ‧ Computer Graphics computazioni per frammento rasterizer punti frammenti (punti in R 2) setup (candidati pixels) Z Vertici proiettati computazioni per vertice (punti in R 3) Vertici Rasterizziamo! pixel finali (nello screen-buffer) ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 2/40

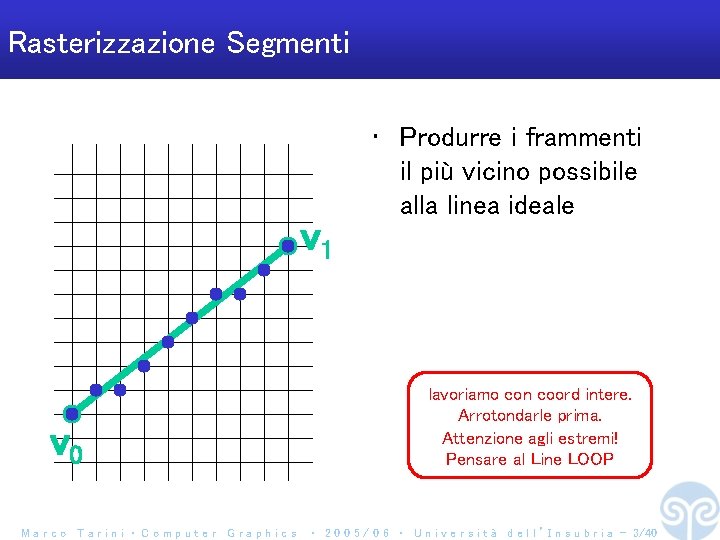
Rasterizzazione Segmenti v 1 v 0 Marco Tarini ‧ Computer Graphics • Produrre i frammenti il più vicino possibile alla linea ideale lavoriamo con coord intere. Arrotondarle prima. Attenzione agli estremi! Pensare al Line LOOP ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 3/40

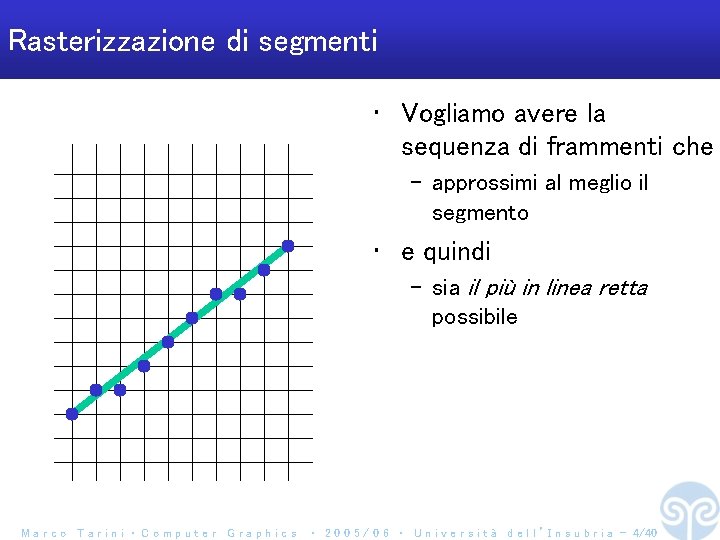
Rasterizzazione di segmenti • Vogliamo avere la sequenza di frammenti che – approssimi al meglio il segmento • e quindi – sia il più in linea retta possibile Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 4/40

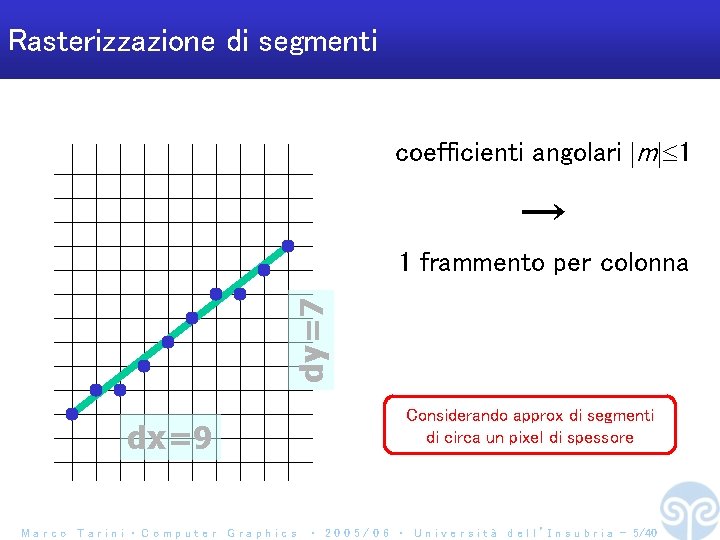
Rasterizzazione di segmenti coefficienti angolari m 1 → dy=7 1 frammento per colonna dx=9 Marco Tarini ‧ Computer Graphics Considerando approx di segmenti di circa un pixel di spessore ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 5/40

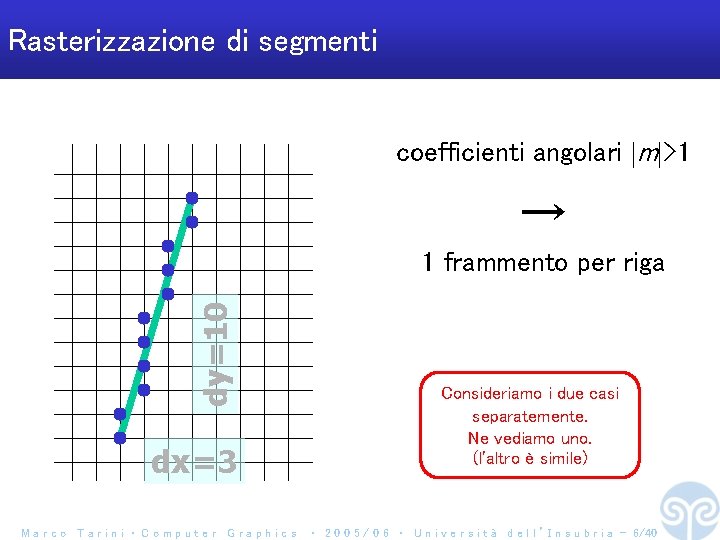
Rasterizzazione di segmenti coefficienti angolari m >1 → dy=10 1 frammento per riga dx=3 Marco Tarini ‧ Computer Graphics Consideriamo i due casi separatemente. Ne vediamo uno. (l'altro è simile) ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 6/40

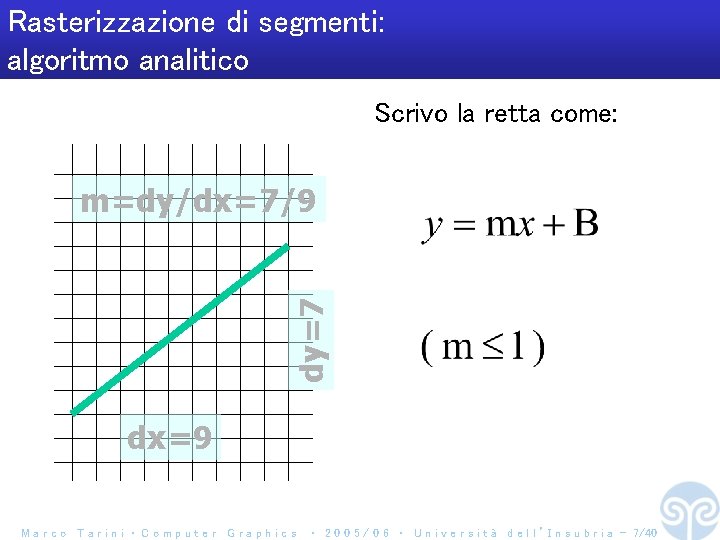
Rasterizzazione di segmenti: algoritmo analitico Scrivo la retta come: dy=7 m=dy/dx=7/9 dx=9 Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 7/40

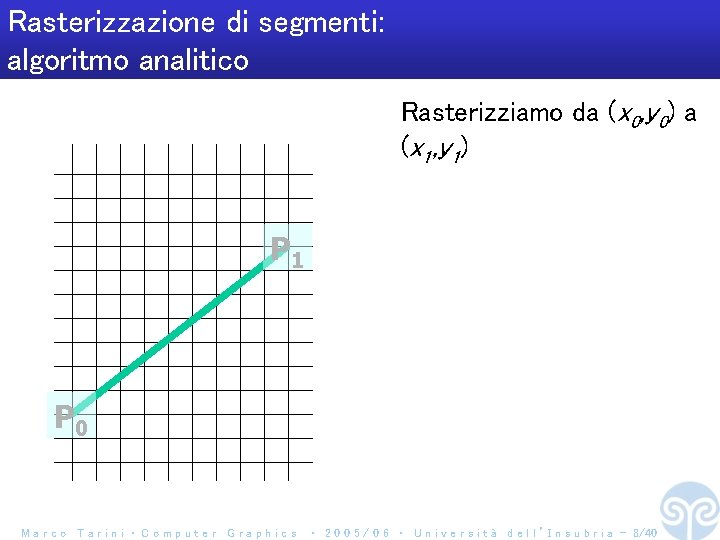
Rasterizzazione di segmenti: algoritmo analitico Rasterizziamo da (x 0, y 0) a (x 1, y 1) P 1 P 0 Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 8/40

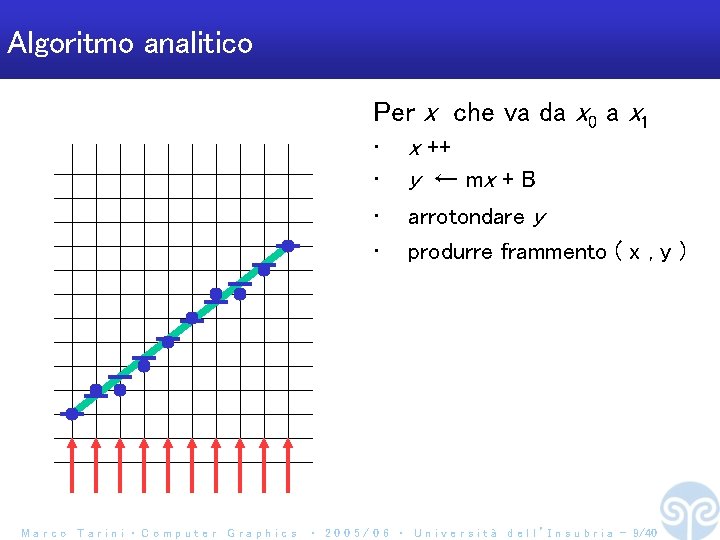
Algoritmo analitico Per x che va da x 0 a x 1 • • Marco Tarini ‧ Computer Graphics x ++ y ← mx + B arrotondare y produrre frammento ( x , y ) ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 9/40

Algoritmo analitico • seleziona sempre il frammento più vicino alla linea ideale • per trovarlo si devono fare: – un’addizione (un +1 intero) – una moltiplicazione (float) – un arrotondamento (da float a int) Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 10/40

Prima ottimizzazione: algoritmo DDA • DDA = Digital Differential Analyzer • Elimina la moltiplicazione • Tecnica incrementale – calcola la nuova y in base alla precedente Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 11/40

Prima ottimizzazione: algoritmo DDA • Banalmente: Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 12/40

Prima ottimizzazione: algoritmo DDA y ← y 0 per x che va da x 0 a x 1 • • x ++ y ← mx + B arrotondare y produrre frammento ( x , y ) algo analitico Marco Tarini ‧ Computer Graphics • • x ++ y +=m operazioni float arrotondare y produrre frammento ( x , y ) algo DDA ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 13/40

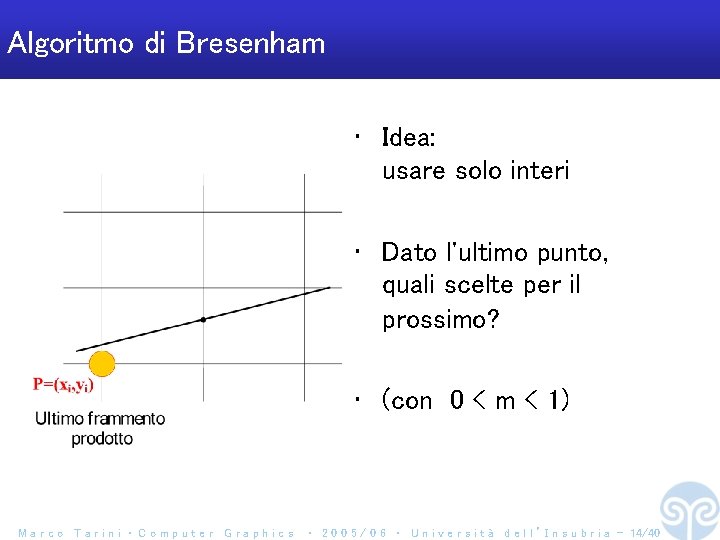
Algoritmo di Bresenham • Idea: usare solo interi • Dato l'ultimo punto, quali scelte per il prossimo? • (con 0 < m < 1) Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 14/40

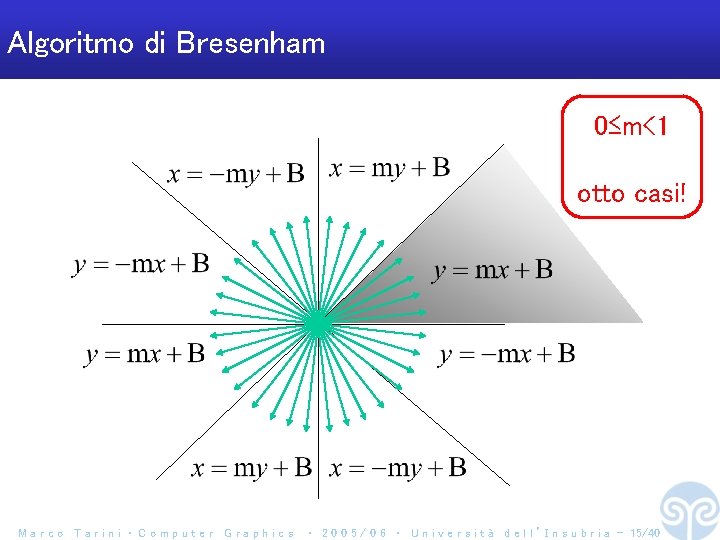
Algoritmo di Bresenham 0≤m<1 otto casi! Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 15/40

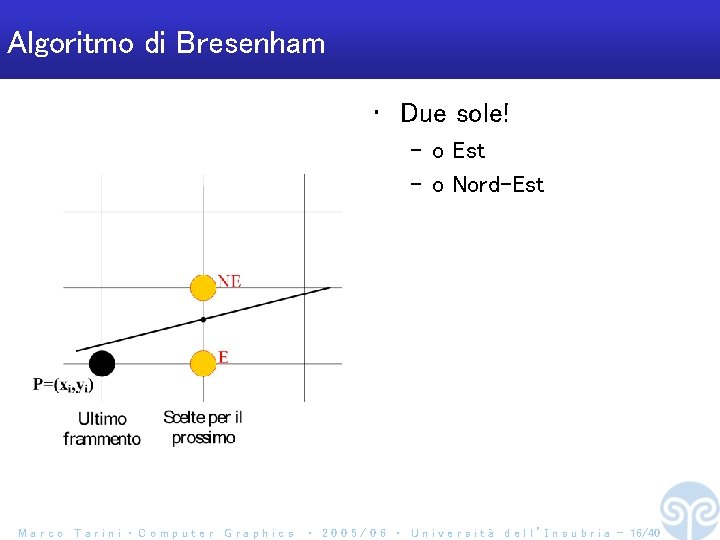
Algoritmo di Bresenham • Due sole! – o Est – o Nord-Est Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 16/40

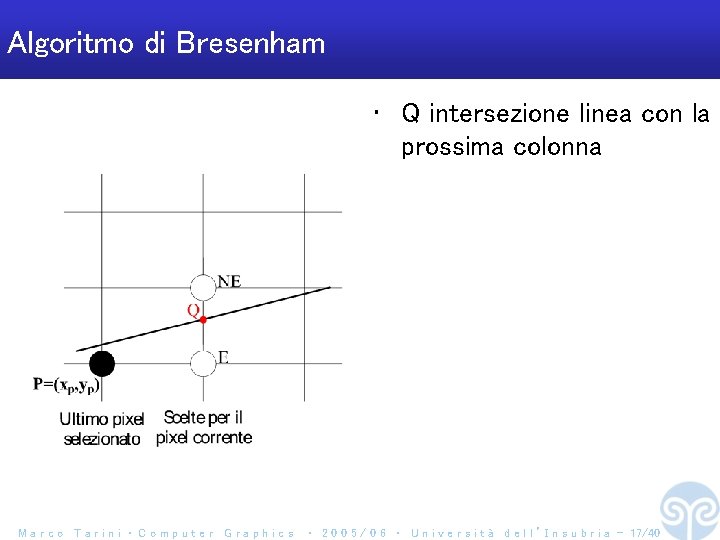
Algoritmo di Bresenham • Q intersezione linea con la prossima colonna Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 17/40

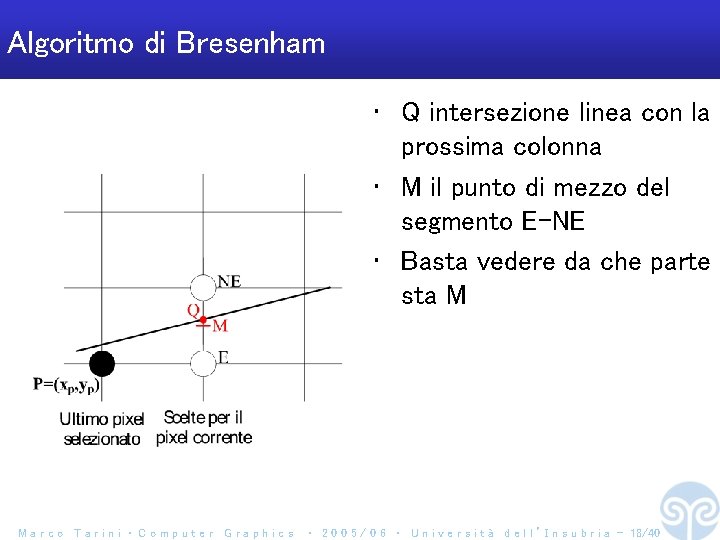
Algoritmo di Bresenham • Q intersezione linea con la prossima colonna • M il punto di mezzo del segmento E-NE • Basta vedere da che parte sta M Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 18/40

Algoritmo di Bresenham • Conviene passare alla forma implicita dell’equazione della retta: Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 19/40

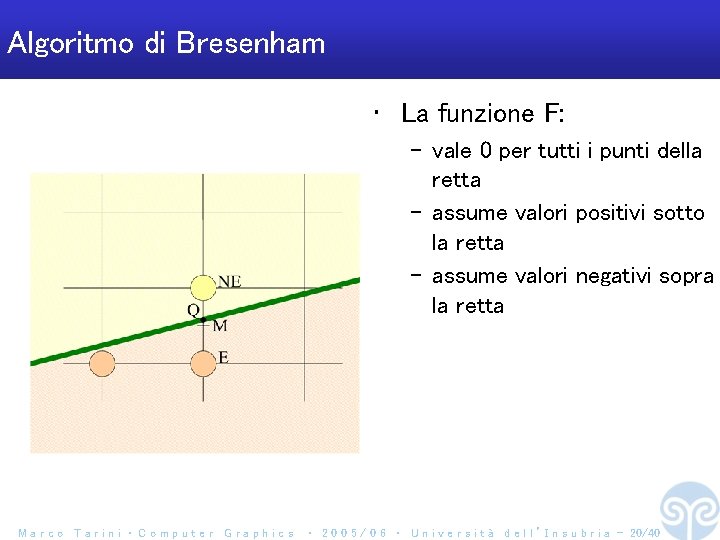
Algoritmo di Bresenham • La funzione F: – vale 0 per tutti i punti della retta – assume valori positivi sotto la retta – assume valori negativi sopra la retta Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 20/40

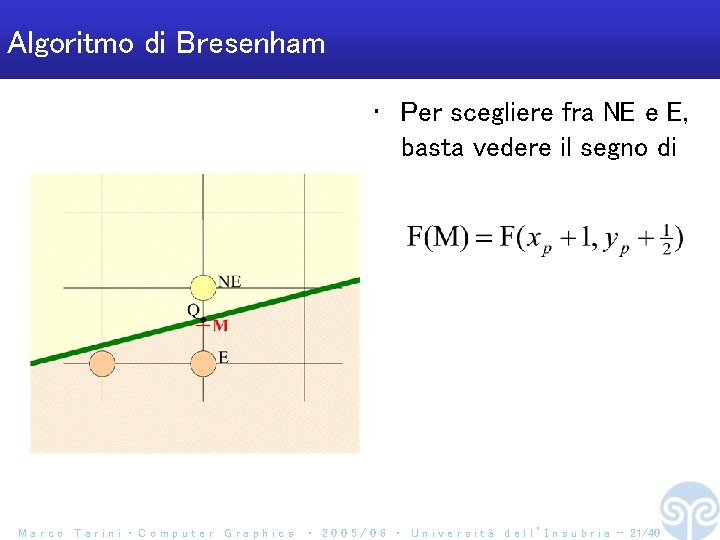
Algoritmo di Bresenham • Per scegliere fra NE e E, basta vedere il segno di Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 21/40

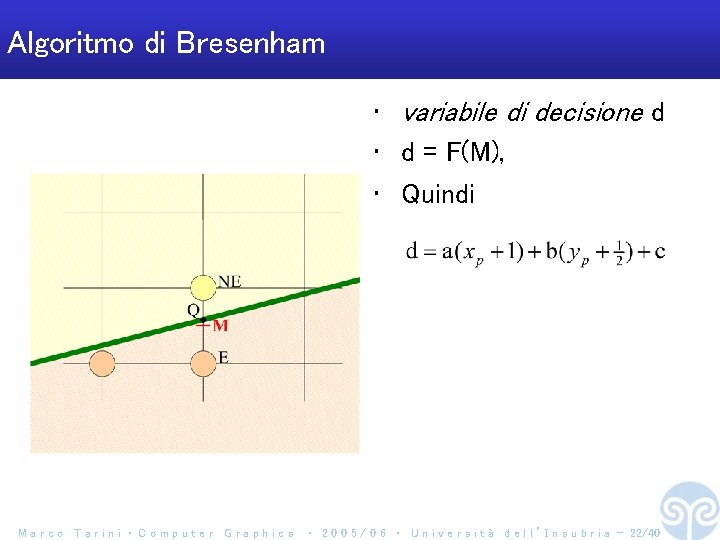
Algoritmo di Bresenham • variabile di decisione d • d = F(M), • Quindi Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 22/40

Algoritmo di Bresenham • d 0 • M sta sopra la retta • Scegliamo E Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 23/40

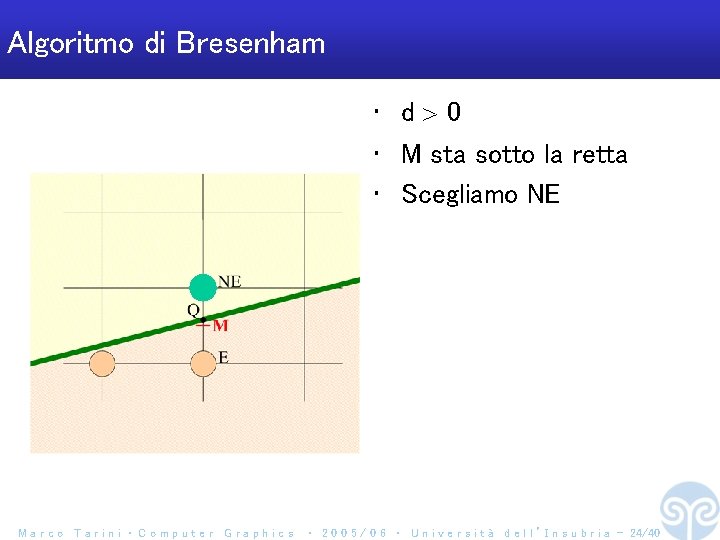
Algoritmo di Bresenham • d 0 • M sta sotto la retta • Scegliamo NE Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 24/40

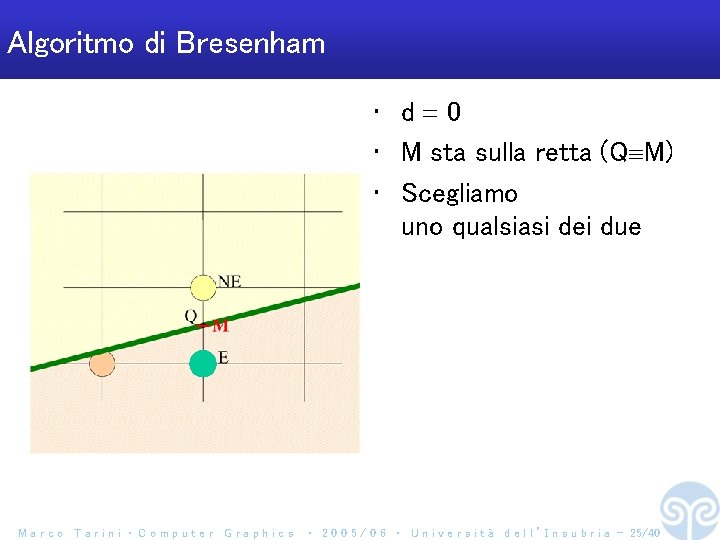
Algoritmo di Bresenham • d 0 • M sta sulla retta (Q M) • Scegliamo uno qualsiasi dei due Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 25/40

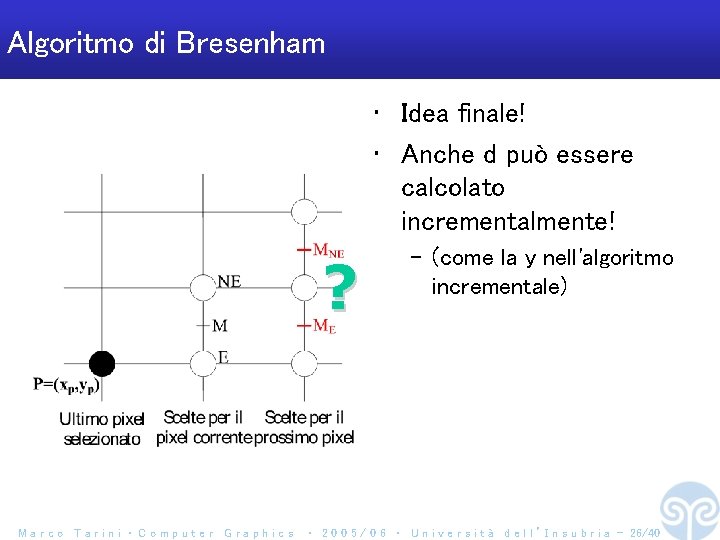
Algoritmo di Bresenham • Idea finale! • Anche d può essere calcolato incrementalmente! ? Marco Tarini ‧ Computer Graphics – (come la y nell'algoritmo incrementale) ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 26/40

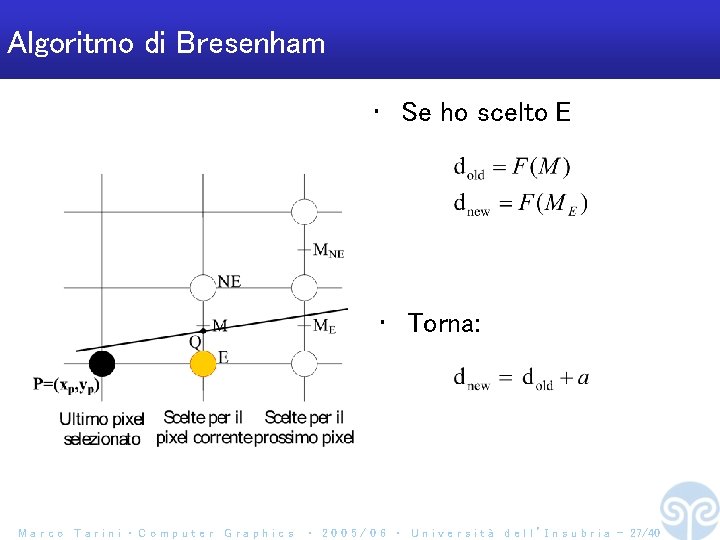
Algoritmo di Bresenham • Se ho scelto E • Torna: Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 27/40

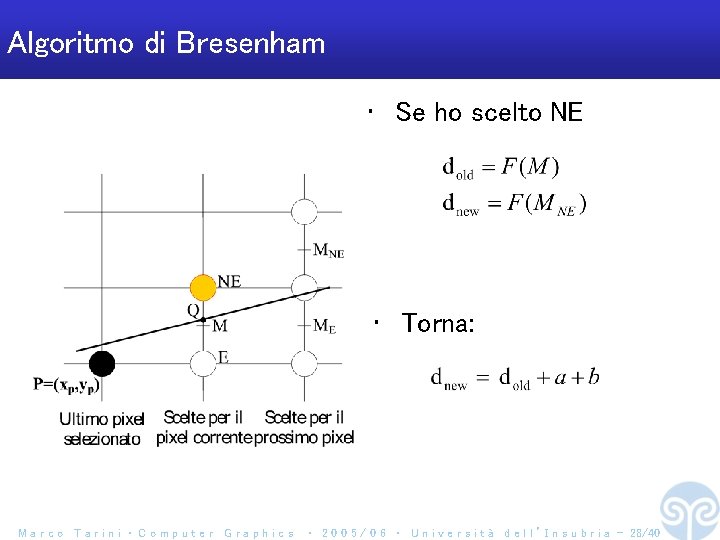
Algoritmo di Bresenham • Se ho scelto NE • Torna: Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 28/40

Algoritmo di Bresenham • Ok, d viene incrementato di una costante • (diversa a seconda se E o NE) • E il valore iniziale? • (x 0, y 0) appartiene alla retta e F(x 0, y 0) 0 Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 29/40

Algoritmo di Bresenham Midpoint. Line(int x 0, int y 0, int x 1, int y 1) { int dx, dy, incr. E, incr. NE, d, x, y; Inizializzazione Variabili intere dy = y 1 -y 0; while (x < x 1 ) { if ( d <= 0 ) { d = d+incr. E; x++; } else { d = d+incr. NE; x++; y++; } Spara. Frammento(x, y); } Scelta di E Scelta di dx = x 1 -x 0; d = 2*dy-dx; incr. E = 2*dy; incr. NE = 2*(dy-dx); x = x 0; y = y 0; Moltiplico per 2 NE per avere solo interi } Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 30/40

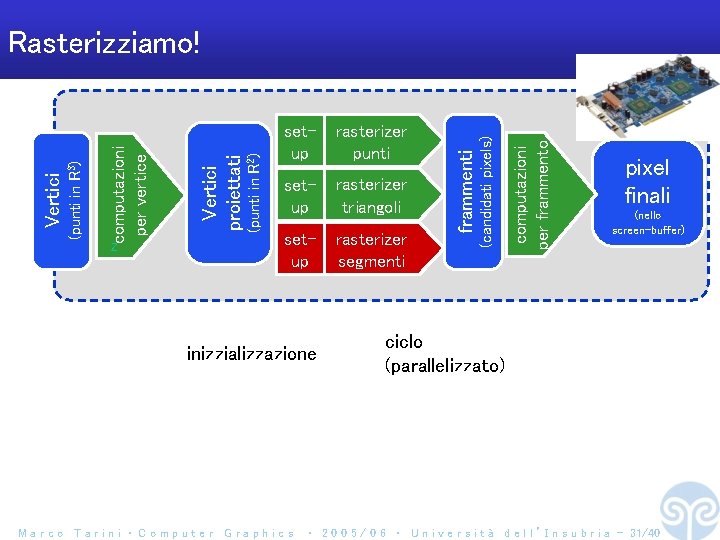
setup rasterizer triangoli setup rasterizer segmenti inizzializzazione Marco Tarini ‧ Computer Graphics computazioni per frammento rasterizer punti frammenti (punti in R 2) setup (candidati pixels) Z Vertici proiettati computazioni per vertice (punti in R 3) Vertici Rasterizziamo! pixel finali (nello screen-buffer) ciclo (parallelizzato) ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 31/40

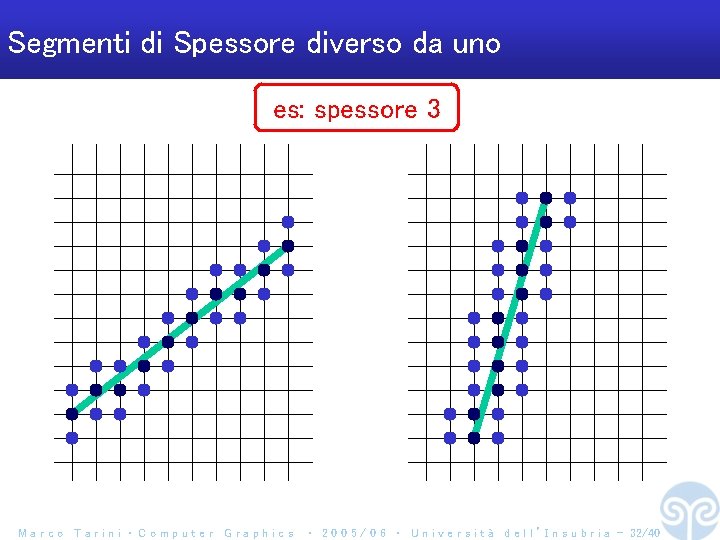
Segmenti di Spessore diverso da uno es: spessore 3 Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 32/40

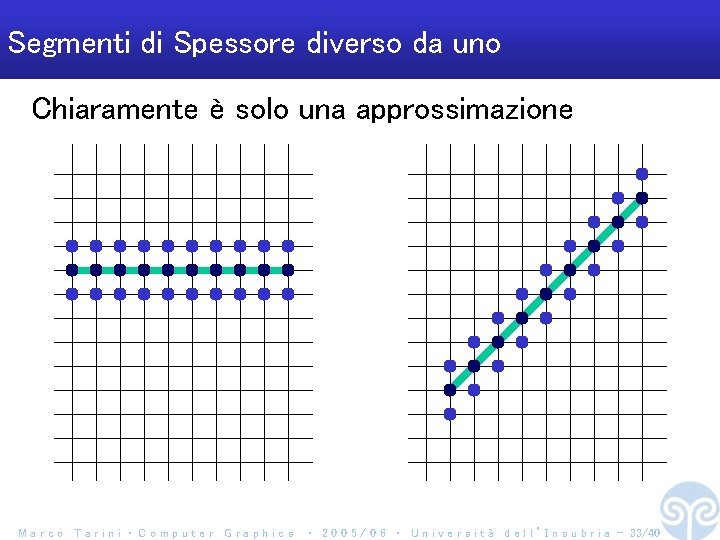
Segmenti di Spessore diverso da uno Chiaramente è solo una approssimazione Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 33/40

Segmenti di Spessore diverso da uno • In Open. GL void gl. Line. Width( width ); Non necessariamente un intero (se si usa anti-aliasing, vedi poi) Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 34/40

setup rasterizer triangoli setup rasterizer segmenti Marco Tarini ‧ Computer Graphics computazioni per frammento rasterizer punti frammenti (punti in R 2) setup (candidati pixels) Z Vertici proiettati computazioni per vertice (punti in R 3) Vertici Rasterizziamo! pixel finali (nello screen-buffer) ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 35/40

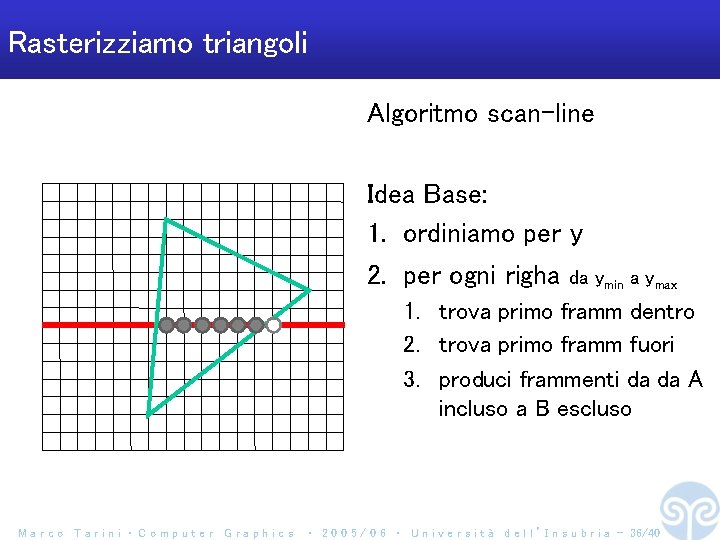
Rasterizziamo triangoli Algoritmo scan-line Idea Base: 1. ordiniamo per y 2. per ogni righa da ymin a ymax 1. trova primo framm dentro 2. trova primo framm fuori 3. produci frammenti da da A incluso a B escluso Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 36/40

Rasterizziamo triangoli Algoritmo scan-line Idea Base: 1. ordiniamo per y 2. per ogni righa da ymin a ymax 1. trova primo framm dentro 2. trova primo framm fuori 3. produci frammenti da primo dentro a primo fuori (escluso) Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 37/40

Bresenham • In ogni riga: – trovare il primo-dentro e primo-fuori è simile a Bresenham, ma: • un caso solo (sempre per riga, sempre verso l'alto) • arrotondiamo sempre per eccesso • passiamo all'altro segmento quando siamo arrivati alla riga del punto in mezzo Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 38/40

Terminologie circa la rasterizzazione triangoli • "Scan-Conversion" = Rasterization (Rasterizzazione) • • • "to scan-conver" = to Rasterize "Span" = intervallo da primo-dentro a primo-fuori "Line-scan" = una riga processata "Active edges" = i 2 lati attuali "Edge tables" = i 33 lati (precalcolati) Nel nostro caso (triangoli)! In generale, N e N (poligoni generici) Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 39/40

Problemi con rasterizzazione di poligoni usando scan-line • I frammenti vengono prodotti uno alla volta • Non adatto ad una implementazione parallela – il rasterizzatore deve produrre frammenti molto velocemente (cioè molti alla volta) se non vogliamo tenere disoccupato il processore di frammenti Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 40/40

Soluzione • Produrre frammenti a gruppi – ad es, a gruppi di 2 x 2 o 4 x 4 o 4 x 1 o 8 x 1. . . • Non necessariamente tutti i componenti di un gruppo sono frammenti interni al triangolo • Testare ogni frammento: – scartare quelli interni Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 41/40

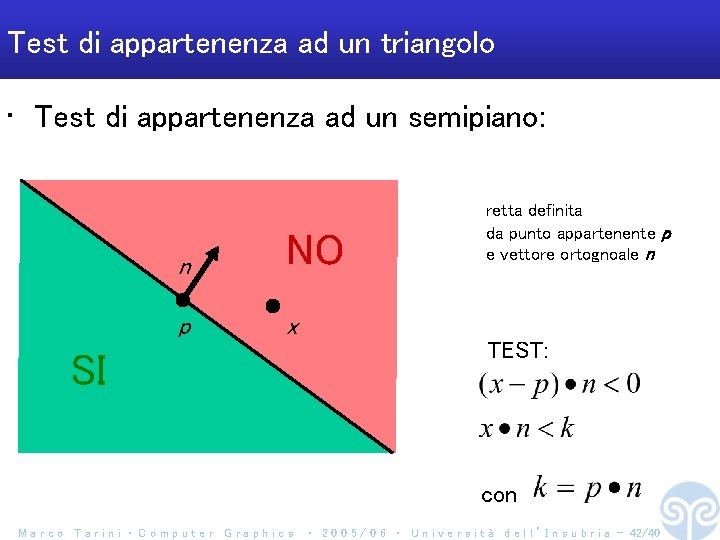
Test di appartenenza ad un triangolo • Test di appartenenza ad un semipiano: n NO p x SI retta definita da punto appartenente p e vettore ortognoale n TEST: con Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 42/40

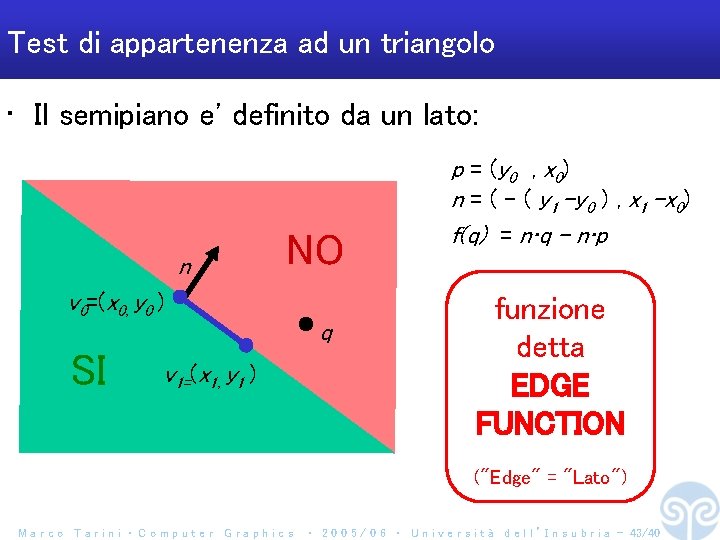
Test di appartenenza ad un triangolo • Il semipiano e' definito da un lato: n NO v 0=(x 0, y 0 ) SI v 1=(x 1, y 1 ) q p = (y 0 , x 0) n = ( - ( y 1 -y 0 ) , x 1 -x 0) f(q) = n‧q - n‧p funzione detta EDGE FUNCTION ("Edge" = "Lato") Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 43/40

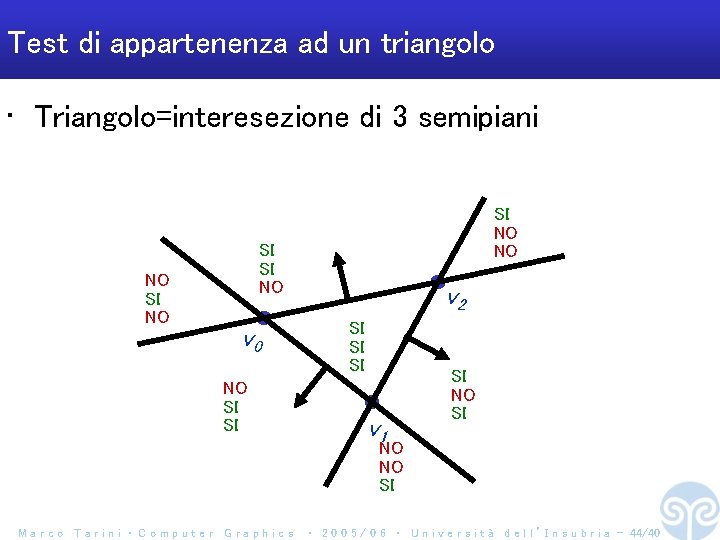
Test di appartenenza ad un triangolo • Triangolo=interesezione di 3 semipiani NO SI NO NO SI SI NO v 0 NO SI SI v 2 SI SI SI v 1 SI NO NO SI Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 44/40

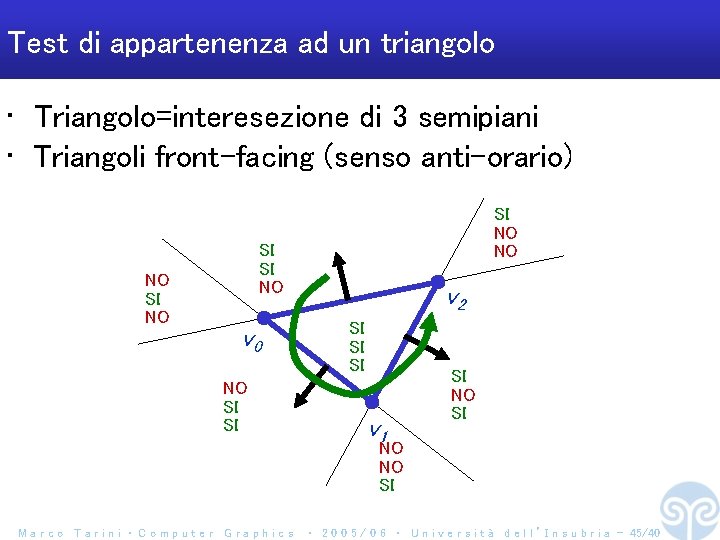
Test di appartenenza ad un triangolo • Triangolo=interesezione di 3 semipiani • Triangoli front-facing (senso anti-orario) NO SI NO NO SI SI NO v 0 NO SI SI v 2 SI SI SI v 1 SI NO NO SI Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 45/40

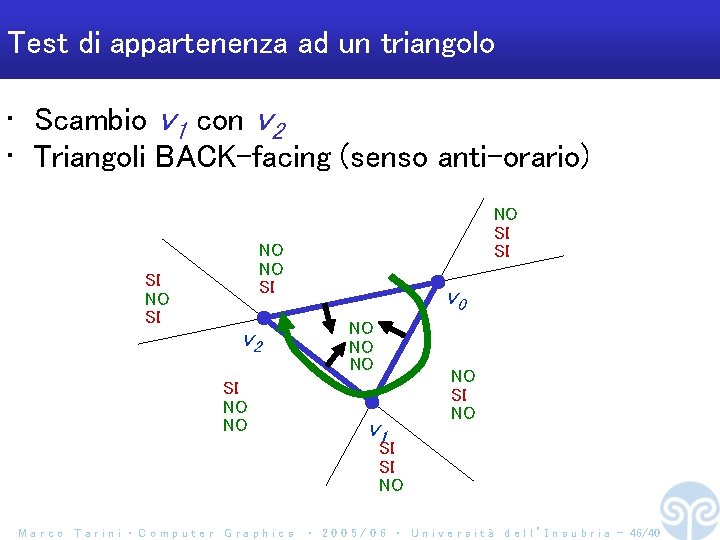
Test di appartenenza ad un triangolo • Scambio v 1 con v 2 • Triangoli BACK-facing (senso anti-orario) SI NO SI SI NO NO SI v 2 SI NO NO v 0 NO NO NO v 1 NO SI SI NO Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 46/40

Test di appartenenza ad un triangolo Tre Edge Functions: (una per lato) • Tutte SI (negative) : – frammento interno a triangolo front-facing • Tutte NO (positive): – frammento interno a triangolo back-facing • Miste: – frammento esterno (scartare sempre) Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 47/40

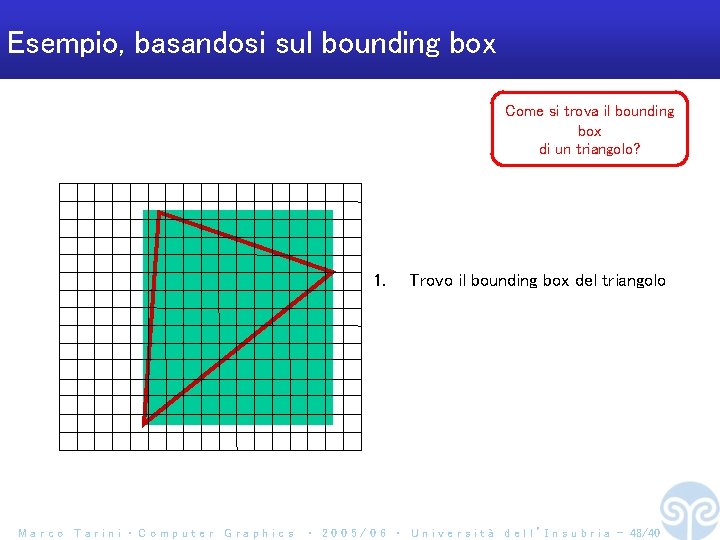
Esempio, basandosi sul bounding box Come si trova il bounding box di un triangolo? 1. Marco Tarini ‧ Computer Graphics Trovo il bounding box del triangolo ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 48/40

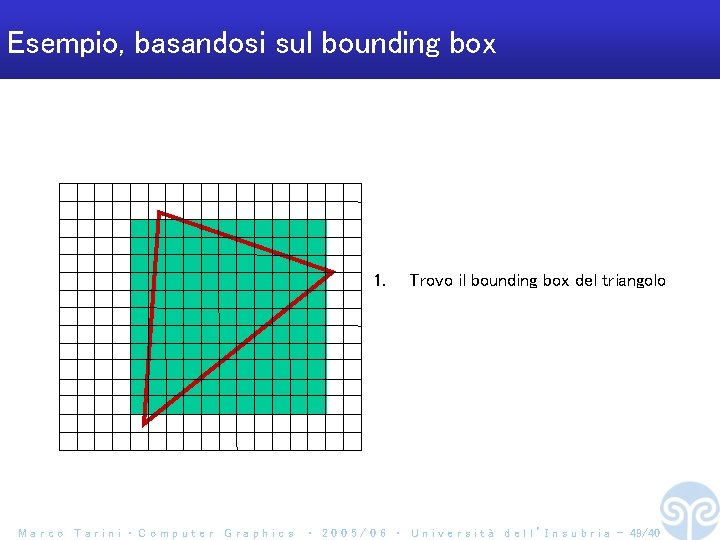
Esempio, basandosi sul bounding box 1. Marco Tarini ‧ Computer Graphics Trovo il bounding box del triangolo ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 49/40

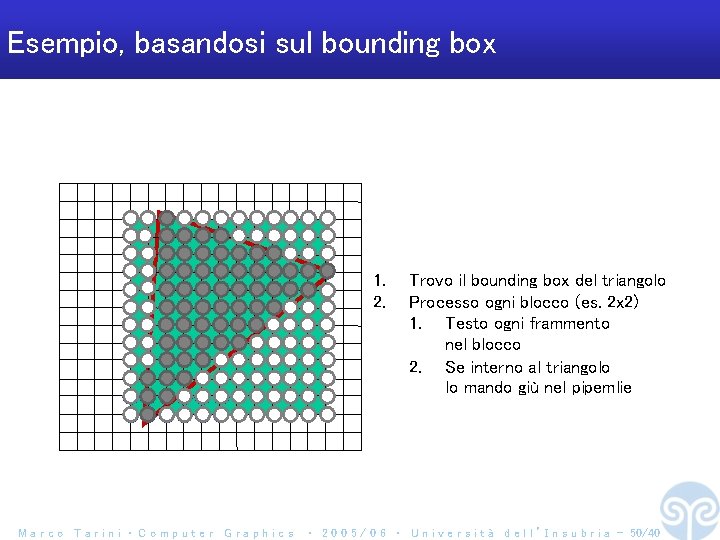
Esempio, basandosi sul bounding box 1. 2. Marco Tarini ‧ Computer Graphics Trovo il bounding box del triangolo Processo ogni blocco (es. 2 x 2) 1. Testo ogni frammento nel blocco 2. Se interno al triangolo lo mando giù nel pipemlie ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 50/40

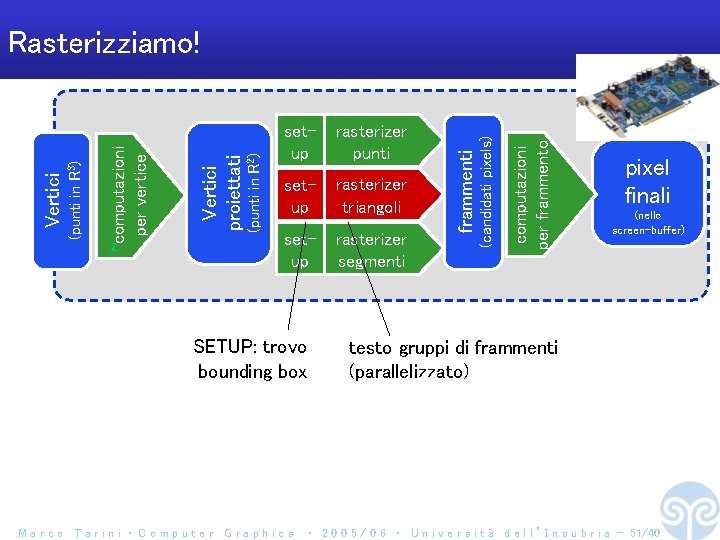
setup rasterizer triangoli setup rasterizer segmenti SETUP: trovo bounding box Marco Tarini ‧ Computer Graphics computazioni per frammento rasterizer punti frammenti (punti in R 2) setup (candidati pixels) Z Vertici proiettati computazioni per vertice (punti in R 3) Vertici Rasterizziamo! pixel finali (nello screen-buffer) testo gruppi di frammenti (parallelizzato) ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 51/40

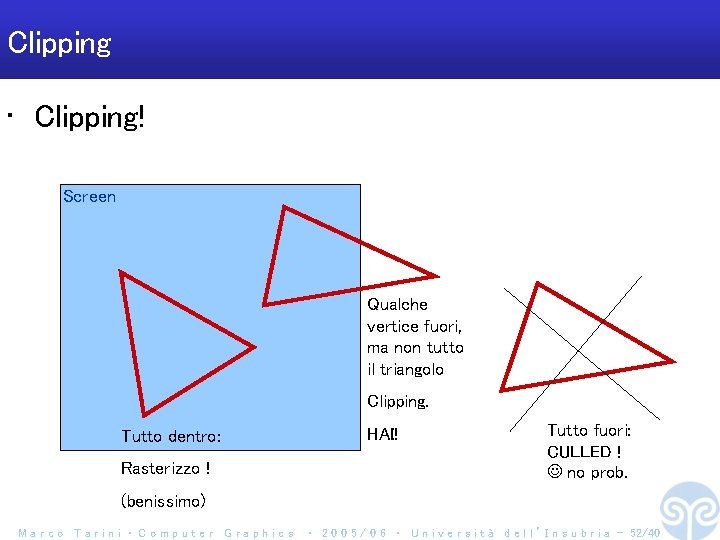
Clipping • Clipping! Screen Qualche vertice fuori, ma non tutto il triangolo Clipping. Tutto dentro: Rasterizzo ! HAI! Tutto fuori: CULLED ! no prob. (benissimo) Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 52/40

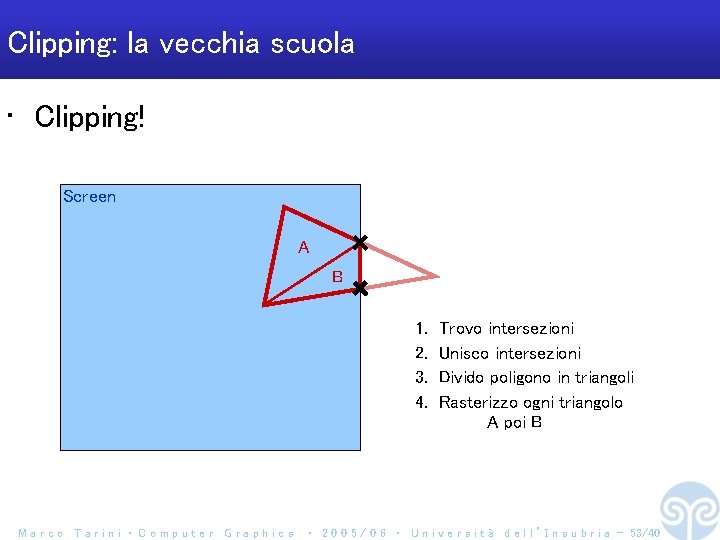
Clipping: la vecchia scuola • Clipping! Screen A B 1. 2. 3. 4. Marco Tarini ‧ Computer Graphics Trovo intersezioni Unisco intersezioni Divido poligono in triangoli Rasterizzo ogni triangolo A poi B ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 53/40

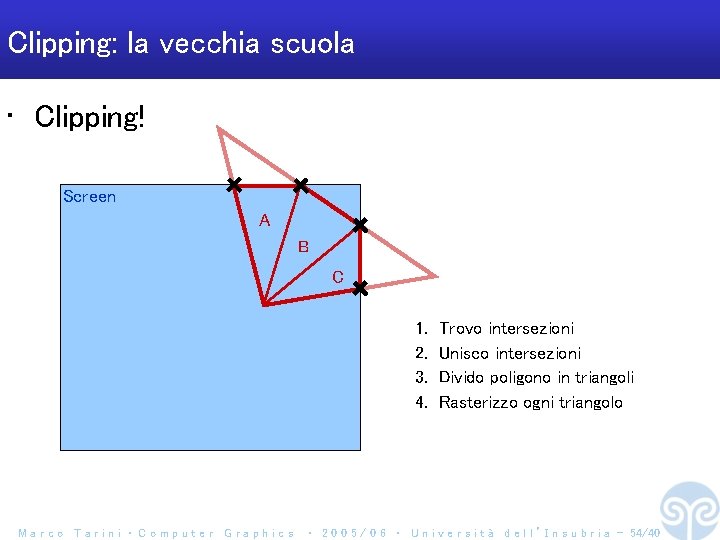
Clipping: la vecchia scuola • Clipping! Screen A B C 1. 2. 3. 4. Marco Tarini ‧ Computer Graphics Trovo intersezioni Unisco intersezioni Divido poligono in triangoli Rasterizzo ogni triangolo ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 54/40

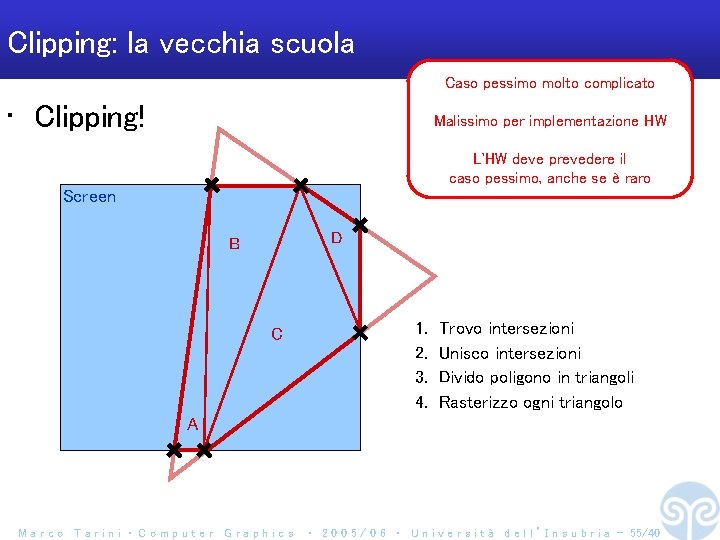
Clipping: la vecchia scuola Caso pessimo molto complicato • Clipping! Malissimo per implementazione HW L'HW deve prevedere il caso pessimo, anche se è raro Screen D B C 1. 2. 3. 4. Trovo intersezioni Unisco intersezioni Divido poligono in triangoli Rasterizzo ogni triangolo A Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 55/40

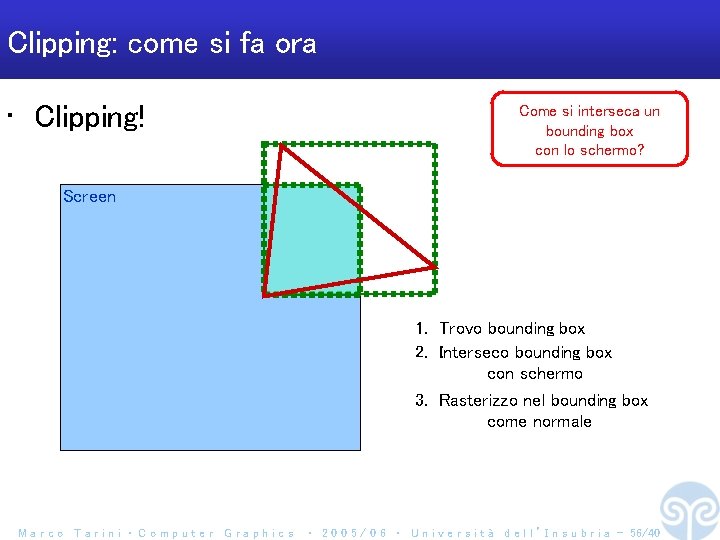
Clipping: come si fa ora • Clipping! Come si interseca un bounding box con lo schermo? Screen 1. Trovo bounding box 2. Interseco bounding box con schermo 3. Rasterizzo nel bounding box come normale Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 56/40

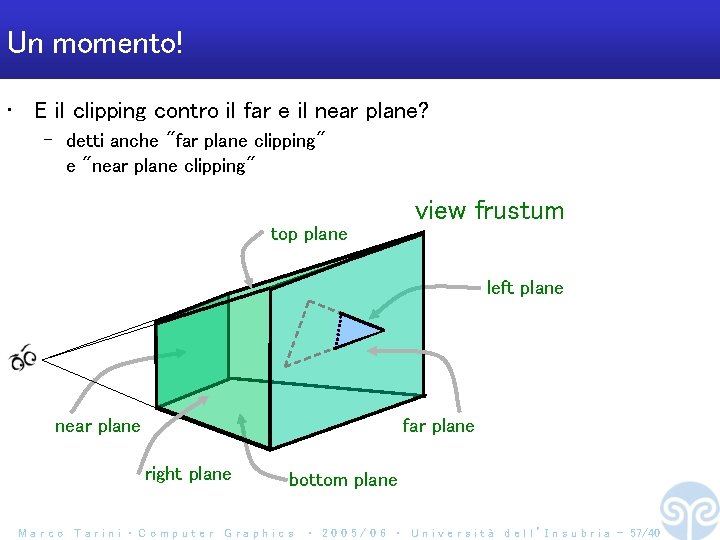
Un momento! • E il clipping contro il far e il near plane? – detti anche "far plane clipping" e "near plane clipping" view frustum top plane left plane near plane far plane right plane bottom plane Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 57/40

Rasterizzazione triangoli: • Il metodo basato su bounding box e test di appartenenza (edge functions): – Vantaggi • fortemente parallelizzabile – (gruppi 4 x 4) • clipping diventa facile – per i planes UP, DOWN, LEFT e RIGHT – Svantaggi • Overhead granding – Si testano molti frammenti inutilmente – Specialmente quando. . . Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 58/40

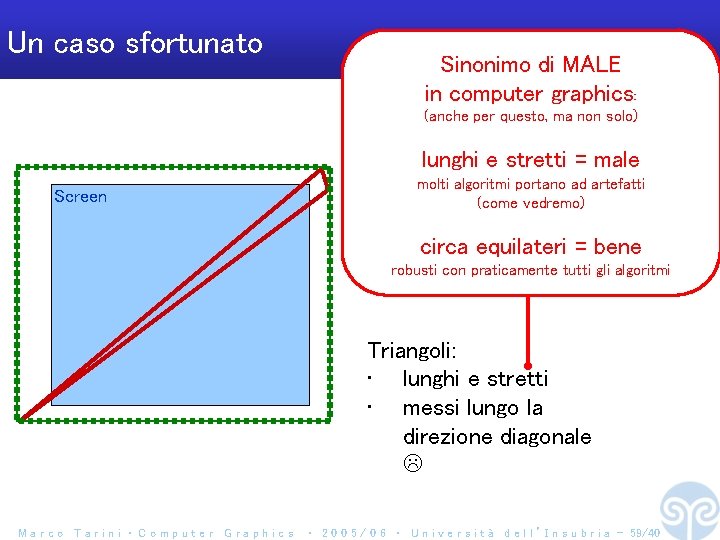
Un caso sfortunato Sinonimo di MALE in computer graphics: (anche per questo, ma non solo) lunghi e stretti = male Screen molti algoritmi portano ad artefatti (come vedremo) circa equilateri = bene robusti con praticamente tutti gli algoritmi Triangoli: • lunghi e stretti • messi lungo la direzione diagonale Marco Tarini ‧ Computer Graphics ‧ 2 0 0 5 / 0 6 ‧ U n i v e r s i t à d e l l ’ I n s u b r i a - 59/40