Computer Graphics Lecture 6 Rasterisation Antialiasing Texture Mapping

Computer Graphics Lecture 6 Rasterisation, Antialiasing, Texture Mapping, Inf 4/MSc

Computer Graphics Inf 4/MSc Some Tutorial about the Project • I have alreadystcovered all the topics needed to finish the 1 practical • Today, I will briefly explain how to start working on it. • I have already provided you a program to import an obj file. 2

Computer Graphics Steps Inf 4/MSc • Apply transformations to all vertices • Prepare the frame buffer and Z-buffer • For each triangle • Project it to the screen space • Find the 2 D bounding box • For each pixel in the bounding box • Check if it is inside the triangle by computing its barycentric coordinates • If yes, use barycentric coordinates to compute the depth and colour at the pixel • If (depth < zbuf[pixel]) { framebuffer[pixel] = colour zbuf[pixel] = depth } 3 • Export the frame buffer data into a PPM file

Computer Graphics Inf 4/MSc • For each pixel in the bounding box • Check if it is inside the triangle by computing its barycentric coordinates • If yes, use barycentric coordinates to compute the depth and colour at the pixel z = αz + β z 2 + γ z 3 c = αc + β c 2 + γ c 3 • If (z < zbuf[pixel]) { 1 1 } framebuffer[pixel] = colour zbuf[pixel] = c

Computer Graphics Inf 4/MSc Computing the baricentric coordinates of the interior pixels • The triangle is composed of 3 points p 0 (x 0, y 0), p 1 (x 1, y 1), p 2(x 2, y 2) (α, β, γ) : barycentric coordinates Only if 0<α, β, γ<1, (x, y) is inside the triangle Depth can be computed by αZ 0 + βZ 1 +γZ 2 Can do the same thing for color, normals, textures 5

Computer Graphics Inf 4/MSc Today • Anti-aliasing • Texture mapping – Common texture coordinates mapping – Texture coordinates 6

Computer Graphics Rasterisation Inf 4/MSc • Converts the vertex information output by the geometry pipeline into pixel information needed by the video display – Anti-aliasing – Z-buffer – Texture mapping – Bump mapping – Transparent objects – Drawing lines 7

Computer Graphics Anti-aliasing Inf 4/MSc • Aliasing: distortion artifacts produced when representing a high-resolution signal at a lower resolution. • Anti-aliasing : techniques to remove aliasing Aliased polygons (jagged edges) Anti-aliased polygons 8

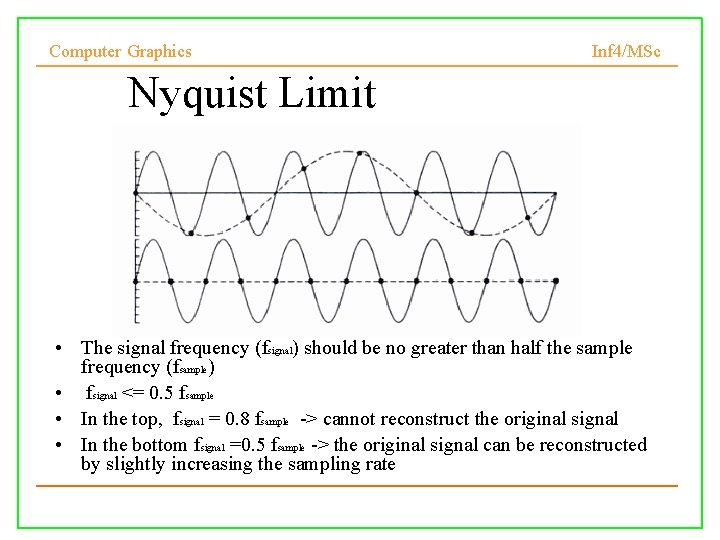
Computer Graphics Inf 4/MSc Nyquist Limit • The signal frequency (fsignal) should be no greater than half the sample frequency (fsample) • fsignal <= 0. 5 fsample • In the top, fsignal = 0. 8 fsample -> cannot reconstruct the original signal • In the bottom fsignal =0. 5 fsample -> the original signal can be reconstructed by slightly increasing the sampling rate

Computer Graphics Inf 4/MSc Screen-based Anti-aliasing Each pixel is subdivided (sub-sampled) into n regions, and each sub-pixel has a color; Compute the average color value 10

Computer Graphics Inf 4/MSc Accumulation Buffer (A-Buffer) • Use a buffer that has the same resolution as the original image • To obtain a 2 x 2 sampling of a scene, 4 images are made by shifting the buffer horizontally/vertically for half a pixel • The results are accumulated and the final results are obtained by averaging • Various sampling schemes are available Pixel center Subsampled point

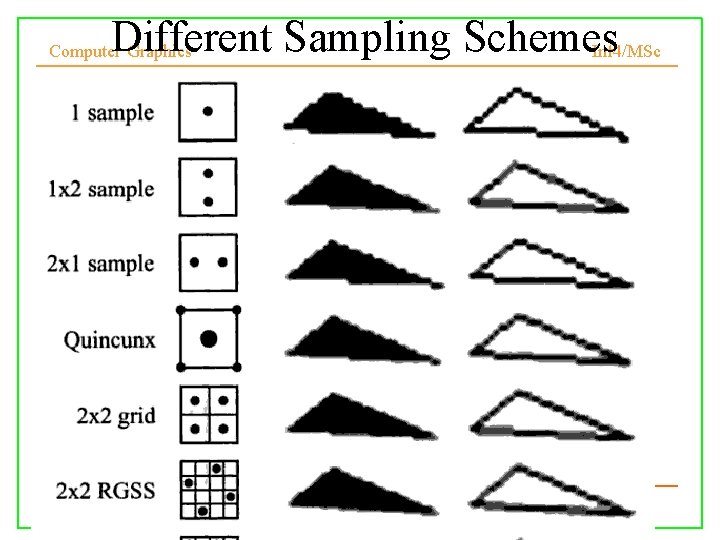
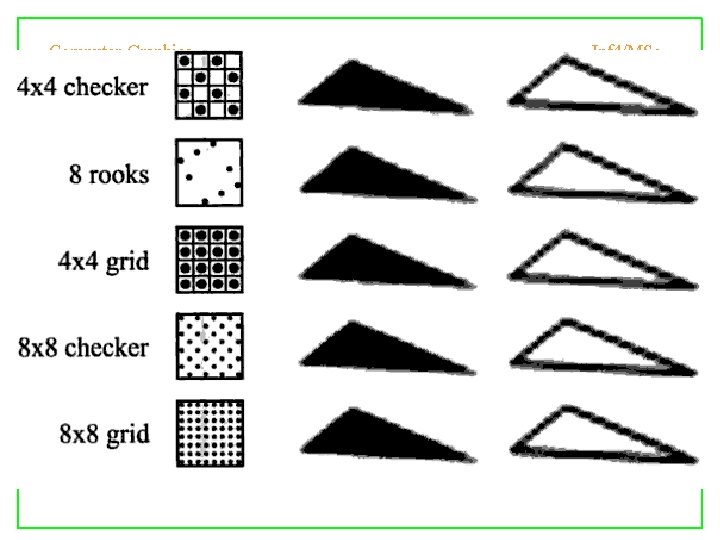
Different Sampling Schemes Inf 4/MSc Computer Graphics

Computer Graphics Inf 4/MSc

Computer Graphics Inf 4/MSc Accumulation Buffer (A-Buffer) • The lighting computation is usually done only once per vertex • Not doing the lighting computation at each sample point • The A-buffer’s focus is on the edge antialiasing • Also useful for rendering transparent objects, motion blur (will be covered later in the course) Edges

Computer Graphics Inf 4/MSc Stochastic Sampling • A scene can be produced of objects that are arbitrarily small • A regular pattern of sampling will always exhibit some sort of aliasing • One approach to solve this is to randomly sample over the pixel – Jittering : subdivide into n regions of equal size and randomly sample inside each region

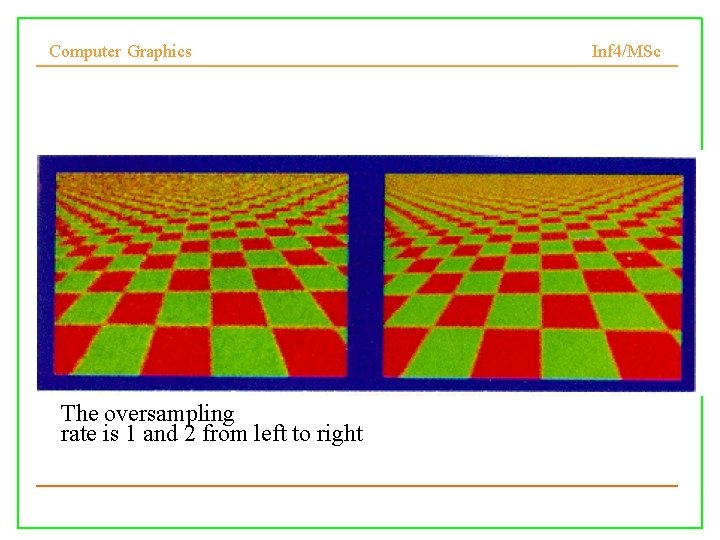
Computer Graphics The oversampling rate is 1 and 2 from left to right Inf 4/MSc

Computer Graphics Inf 4/MSc Today • Anti-aliasing • Texture mapping – Common texture coordinates mapping – Texture coordinates 17

Computer Graphics Inf 4/MSc Texture Mapping : Why needed? • We don't want to represent all this detail with geometry

Computer Graphics Inf 4/MSc Texture mapping. • Method of improving surface appearance by adding details on surface. 19

Computer Graphics Inf 4/MSc Texture mapping. • Image is ‘pasted’ onto a polygon. • Image is called a Texture map, it’s pixels are often referred as a Texels and have coordinates (u, v) • Texture coordinates are defined for each vertex of the polygon and interpolated across the polygon. y v v u u x 20

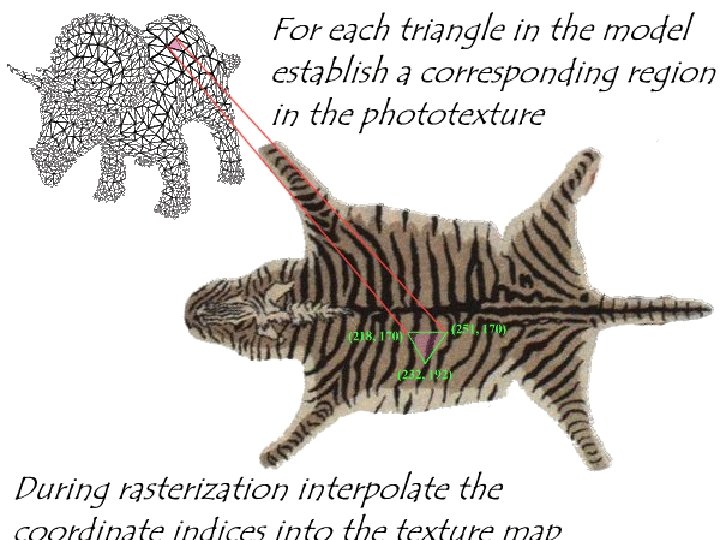
Computer Graphics Inf 4/MSc Photo-textures

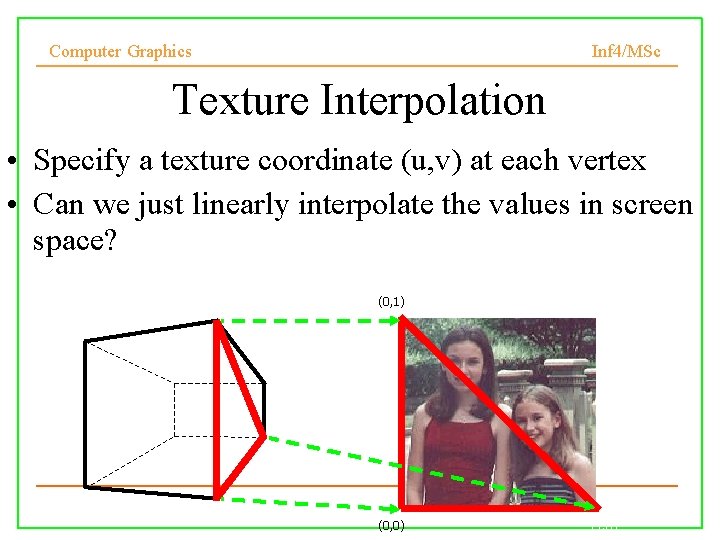
Computer Graphics Inf 4/MSc Texture Interpolation • Specify a texture coordinate (u, v) at each vertex • Can we just linearly interpolate the values in screen space? (0, 1) (0, 0) (1, 0)

Computer Graphics Inf 4/MSc Interpolating the uv coordinates Again, we use baricentric coordinates u 1 v 1 u 3 v 3 u= α u + β u 2 + γ u 3 v = α v + β v 2 + γ v 3 1 1 u 2 v 2

Computer Graphics Interpolation - What Goes Wrong? Inf 4/MSc • Linear interpolation in screen space: texture source what we get| what we want

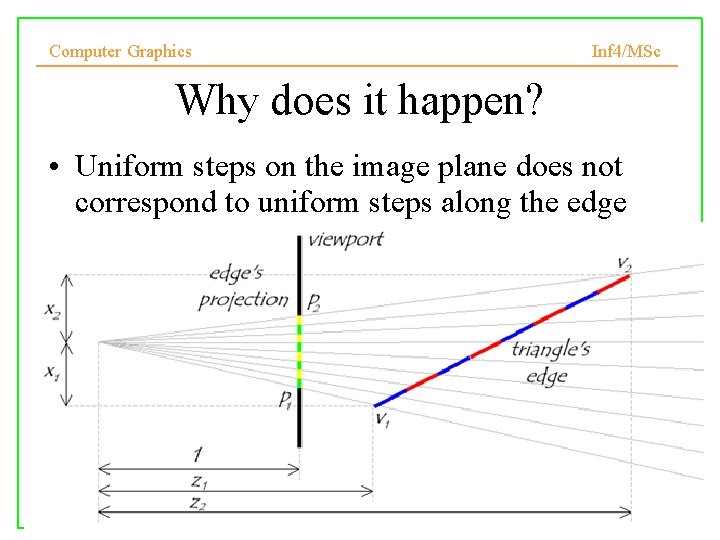
Computer Graphics Inf 4/MSc Why does it happen? • Uniform steps on the image plane does not correspond to uniform steps along the edge

Computer Graphics Inf 4/MSc How do we deal with it? • Use hyperbolic interpolation – (u, v) cannot be linearly interpolated, but 1/w and (u/w, v/w) can – w is the last component after the canonical view transformation

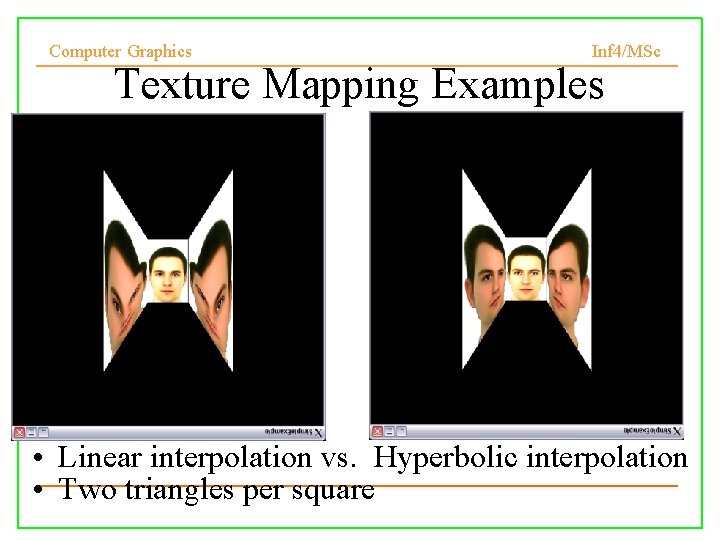
Computer Graphics Inf 4/MSc Texture Mapping Examples • Linear interpolation vs. Hyperbolic interpolation • Two triangles per square

Computer Graphics Inf 4/MSc Computing the uv coordinates at the internal points • For three points of the triangle, get • Compute at the internal points of the triangle by interpolation • Compute wi by inverting 1/wi, and multiply them to (ui /wi, , vi /wi) to compute (ui, vi)

Computer Graphics Inf 4/MSc Common Texture Coordinate Mappings • Orthogonal • Cylindrical • Spherical

Computer Graphics Inf 4/MSc Texture Mapping & Illumination • Texture mapping can be used to alter some or all of the constants in the illumination equation: – pixel color, diffuse color …. Phong’s Illumination Model Constant Diffuse Color Diffuse Texture Color Texture used as Label Texture used as Diffuse Color

Computer Graphics Inf 4/MSc Readings • Chapter 5. 1 -2 of Real-Time Rendering Second edition – http: //books. google. co. uk/books? id=m. OKEf. BT w 4 x 0 C&printsec=frontcover&source=gbs_v 2_ summary_r&cad=0#v=onepage&q=&f=false • “Hyperbolic Interpolation” IEEE Computer Graphics and Applications, vol 12, no. 4, 8994, 1992 • Demoed Software http: //www-ui. is. s. u-tokyo. ac. jp/~takeo/java/smoothteddy/index. html