Computer Graphics Lecture 13 Curves and Surfaces I

Computer Graphics Lecture 13 Curves and Surfaces I

Computer Graphics Types of Curves / Surfaces • Explicit: y = mx + b z = A x + By + C • Implicit: Ax + By + C = 0 (x – x 0)2 + (y – y 0)2 – r 2 = 0 • Parametric: x = x 0 + (x 1 – x 0)t y = y 0 + (y 1 – y 0)t 10/10/2008 Lecture 5 x = x 0 + rcos y = y 0 + rsin 2

Computer Graphics Today • Implicit Surfaces – Metaball • Parametric surfaces – Hermite curve – Bezier curve – Biubic patches – Tessalation 10/10/2008 Lecture 5 3

Computer Graphics Implicit Surfaces • Functions in the form of F(x, y, z) = 0 – i. e. Quadric functions Sphere: f(x, y, z) = x 2+ y 2+ z 2 = 0 3/10/2008 Lecture 3 4

Computer Graphics Metaballs • • One type of implicit surface Also known as blobby objects Negative volume to produce hollows Can be used to model smooth surfaces, liquid

Computer Graphics • • Metaballs (2) A point surrounded by a density field The density decreases with distance from the point The density of multiple particles is summed A surface is implied by sampling the area where the density is a predefined threshold

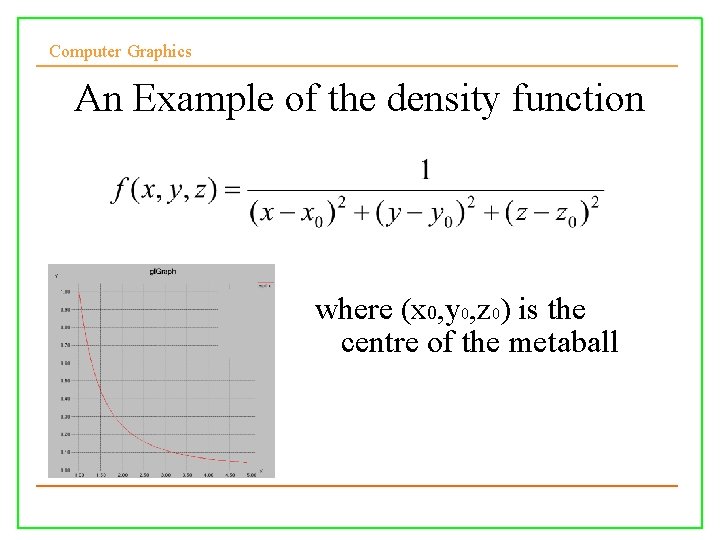
Computer Graphics An Example of the density function where (x 0, y 0, z 0) is the centre of the metaball

Computer Graphics Metaballs (3) • The surface points are sampled and approximated by polygonal meshes for rendering Demo animation of metaballs • http: //www. youtube. com/watch? v=UWv. Gy. K olkho&feature=related • http: //www. youtube. com/watch? v=Nf_Olf. W MRa. A&NR=1

Computer Graphics Today • Implicit Surfaces – Metaball • Parametric surfaces – Hermite curve – Bezier curve – Biubic patches – Tessalation 10/10/2008 Lecture 5 9

Computer Graphics Why parametric? • Parametric curves are very flexible. • Parameter count gives the object’s dimension. (x(u, v), y(u, v), z(u, v)) : 2 D surface • Coord functions independent. 10/10/2008 Lecture 5 10

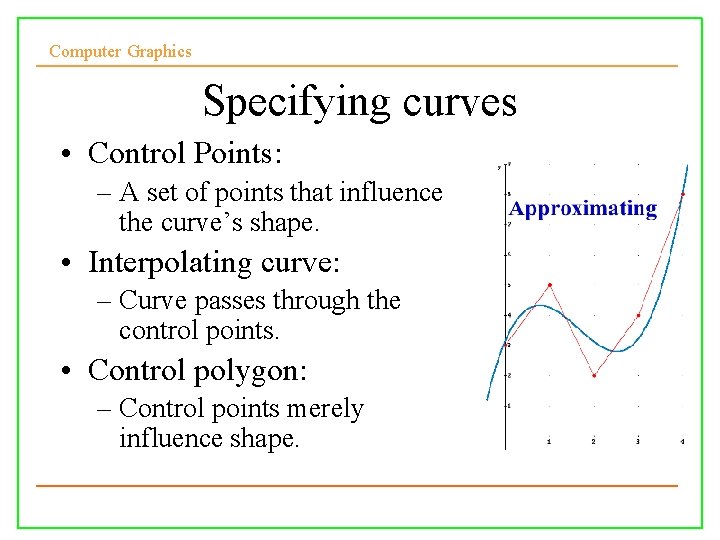
Computer Graphics Specifying curves • Control Points: – A set of points that influence the curve’s shape. • Interpolating curve: – Curve passes through the control points. • Control polygon: – Control points merely influence shape. 10/10/2008 Lecture 5 11

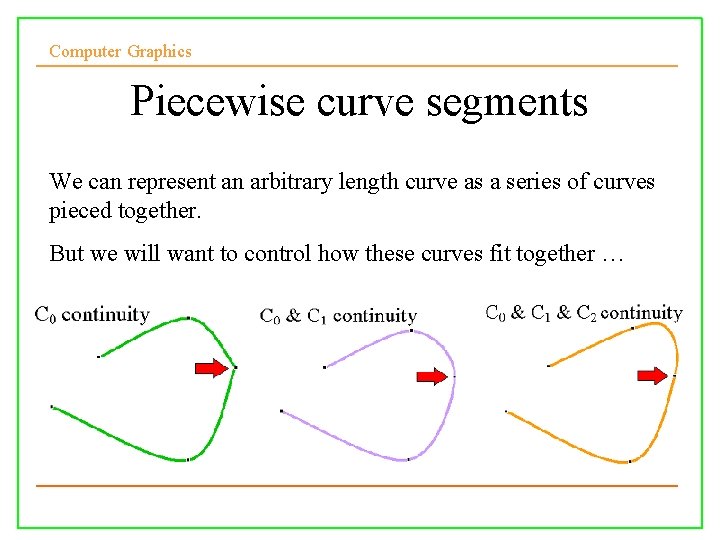
Computer Graphics Piecewise curve segments We can represent an arbitrary length curve as a series of curves pieced together. But we will want to control how these curves fit together … 10/10/2008 Lecture 5 12

Computer Graphics Continuity between curve segments • If the tangent vectors of two cubic curve segments are equal at the join point, the curve has first-degree continuity, and is said to be C 1 continuous • If the direction and magnitude of d n/ dt n[Q(t)] through the nth derivative are equal at the join point, the curve is called Cn continuous • If the directions (but not necessarily the magnitudes) of two segments’ tangent vectors are equal at the join point, the curve has G 1 continuity

Computer Graphics Example • The curves Q 1 Q 2 Q 3 join at point P • Q 1 and Q 2 have equal tangent vectors at P and hence C 1 and G 1 continuous • Q 1 and Q 3 have tangent vectors in the same direction but Q 3 has twice magnitude, so they are only G 1 continuous at P

Computer Graphics Parametric Cubic Curves • In order to assure C 2 continuity our functions must be of at least degree 3. • Cubic has 4 degrees of freedom and can control 4 things. • Use polynomials: x(t) of degree n is a function of t. – – y(t) and z(t) are similar and each is handled independently 10/10/2008 Lecture 5 15

Computer Graphics Hermite curves • A cubic polynomial • Polynomial can be specified by the position of, and gradient at, each endpoint of curve. • Determine: x = X(t) in terms of x 0, x 0’, x 1’ Now: X(t) = a 3 t 3 + a 2 t 2 + a 1 t + a 0 /(t) = 3 a t 2 + 2 a t + a and X 3 5 2 1 10/10/2008 Lecture 16

Computer Graphics Finding Hermite coefficients Substituting for t at each endpoint: x 0 = X(0) = a 0 x 0’= X/(0) = a 1 x 1 = X(1) = a 3 + a 2 + a 1 + a 0 x 1’= X/(1) = 3 a 3 + 2 a 2+ a 1 And the solution is: a 0 = x 0 a 1 = x 0’ a 2 = -3 x 0 – 2 x 0’+ 3 x 1 – x 1’ a 3 = 2 x 0 + x 0’ - 2 x 1 + x 1’ 10/10/2008 Lecture 5 17

Computer Graphics The Hermite matrix: MH The resultant polynomial can be expressed in matrix form: X(t) = t. TMHq ( q is the control vector) We can now define a parametric polynomial for each coordinate required independently, ie. X(t), Y(t) and Z(t) 10/10/2008 Lecture 5 18

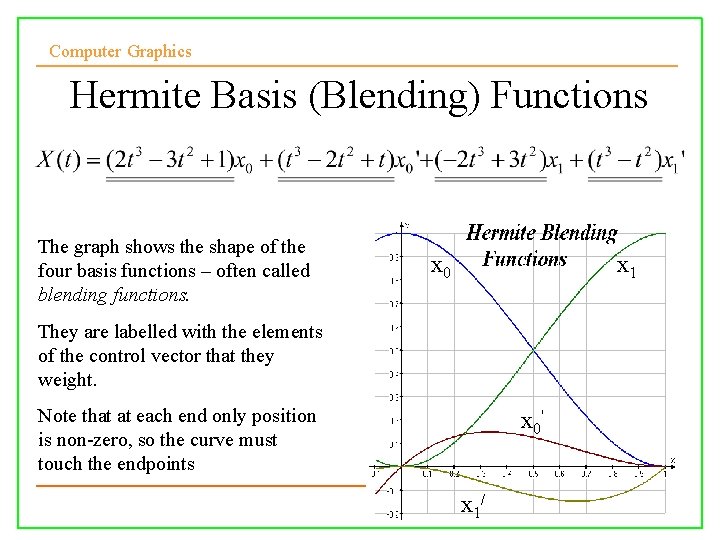
Computer Graphics Hermite Basis (Blending) Functions

Computer Graphics Hermite Basis (Blending) Functions The graph shows the shape of the four basis functions – often called blending functions. x 0 x 1 They are labelled with the elements of the control vector that they weight. Note that at each end only position is non-zero, so the curve must touch the endpoints 10/10/2008 x 0' Lecture 5 x 1/ 20

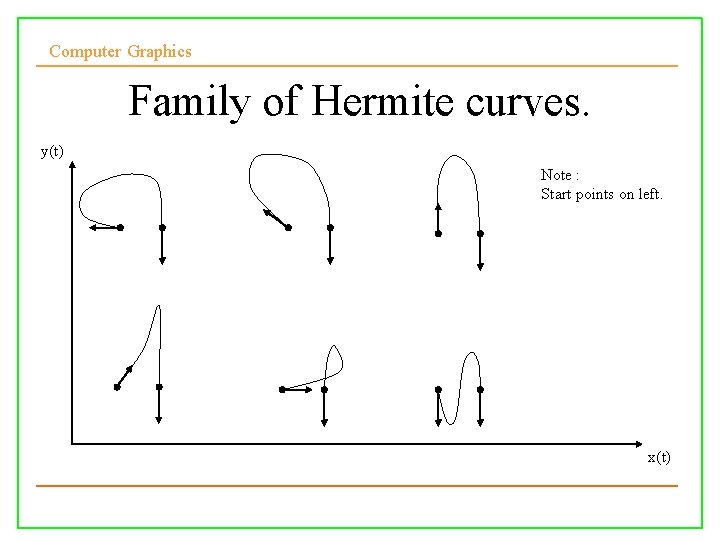
Computer Graphics Family of Hermite curves. y(t) Note : Start points on left. x(t) 10/10/2008 Lecture 5 21

Computer Graphics Displaying Hermite curves. • Simple : – – – Select step size to suit. Plug x values into the geometry matrix. Evaluate P(t) x value for current position. Repeat for y & z independently. Draw line segment between current and previous point. • Joining curves: – Coincident endpoints for C 0 continuity – Align tangent vectors for C 1 continuity 10/10/2008 Lecture 5 . 22

Computer Graphics Bézier Curves • Hermite cubic curves are difficult to model – need to specify point and gradient. • More intuitive to only specify points. • Pierre Bézier (an engineer at Renault) specified 2 endpoints and 2 additional control points to specify the gradient at the endpoints. • Can be derived from Hermite matrix: – Two end control points specify tangent 10/10/2008 Lecture 5 23

Computer Graphics Bézier Curves P 2 Note the Convex Hull has been shown as a dashed line – used as a bounding extent for intersection purposes. P 4 P 1 P 3 P 4 P 2 10/10/2008 Lecture 5 24

Computer Graphics Bézier Matrix • The cubic form is the most popular X(t) = t. TMBq (MB is the Bézier matrix) • With n=4 and r=0, 1, 2, 3 we get: • Similarly for Y(t) and Z(t) 10/10/2008 Lecture 5 25

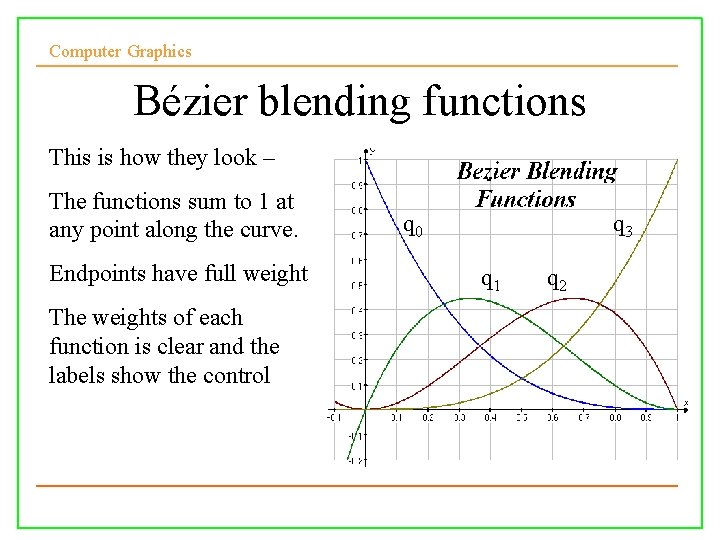
Computer Graphics Bézier blending functions This is how they look – The functions sum to 1 at any point along the curve. q 0 Endpoints have full weight q 3 q 1 q 2 The weights of each function is clear and the labels show the control points being weighted. 10/10/2008 Lecture 5 26

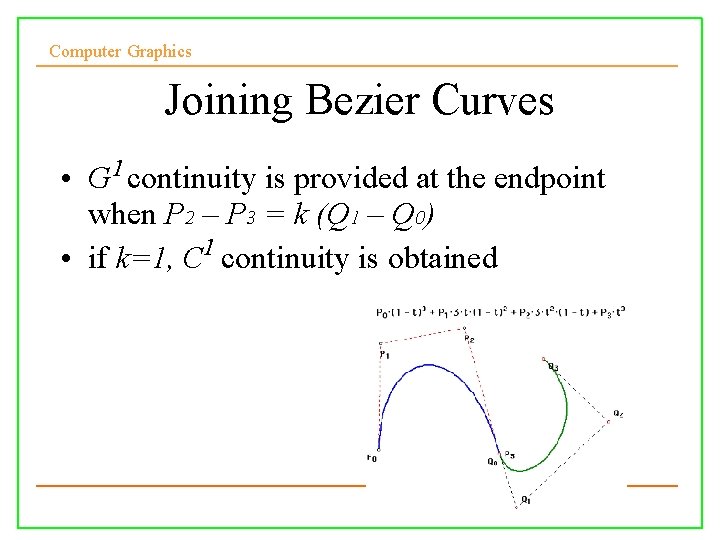
Computer Graphics Joining Bezier Curves • G 1 continuity is provided at the endpoint when P 2 – P 3 = k (Q 1 – Q 0) • if k=1, C 1 continuity is obtained

Computer Graphics Bicubic patches • The concept of parametric curves can be extended to surfaces • The cubic parametric curve is in the form of Q(t)=t. TM q where q=(q 1, q 2, q 3, q 4) : qi control points, M is the basis matrix (Hermite or Bezier, …), t. T=(t 3, t 2, t, 1)

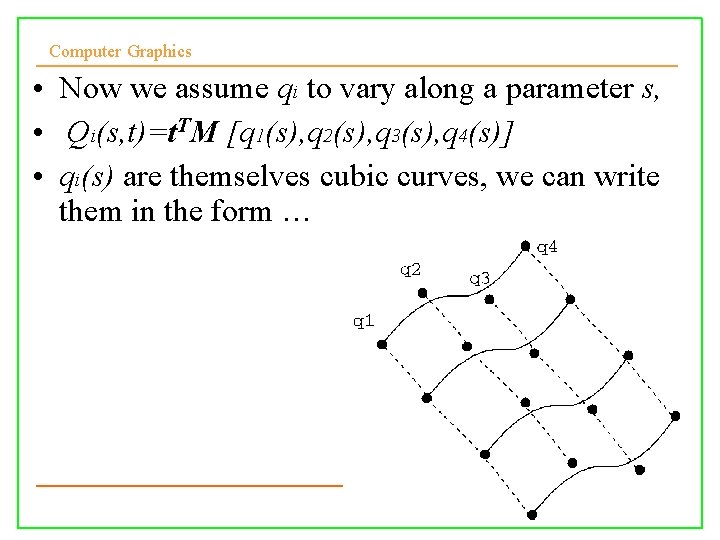
Computer Graphics • Now we assume qi to vary along a parameter s, • Qi(s, t)=t. TM [q 1(s), q 2(s), q 3(s), q 4(s)] • qi(s) are themselves cubic curves, we can write them in the form …

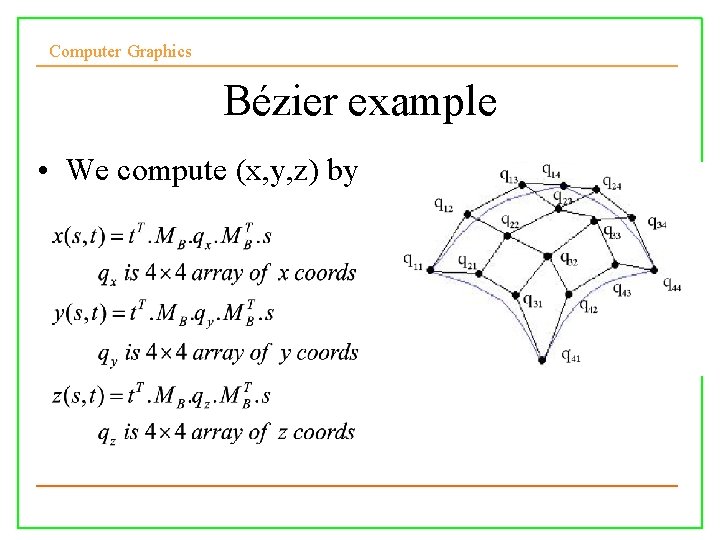
Computer Graphics Bicubic patches where q is a 4 x 4 matrix Each column contains the control points of q 1(s), …, q 4(s) x, y, z computed by

Computer Graphics Bézier example • We compute (x, y, z) by 14/10/2008 Lecture 6 31

Computer Graphics Continuity of Bicubic patches. • Hermite and Bézier patches – C 0 continuity by sharing 4 control points between patches. – C 1 continuity when both sets of control points either side of the edge are collinear with the edge. 14/10/2008 Lecture 6 32

Computer Graphics Displaying Bicubic patches. • Need to compute the normals – vector cross product of the 2 tangent vectors. • Need to convert the bicubic patches into a polygon mesh – tessellation 14/10/2008 Lecture 6 33

Computer Graphics Normal Vectors The surface normal is biquintic (two variables, fifthdegree) polynomial and very expensive Can use finite difference to reduce the computation

Computer Graphics Tessellation • We need to compute the triangles on the surface • The simplest way is do uniform tessellation, which samples points uniformly in the parameter space • Adaptive tessellation – adapt the size of triangles to the shape of the surface – i. e. , more triangles where the surface bends more – On the other hand, for flat areas we do not need many triangles 14/10/2008 Lecture 6 35

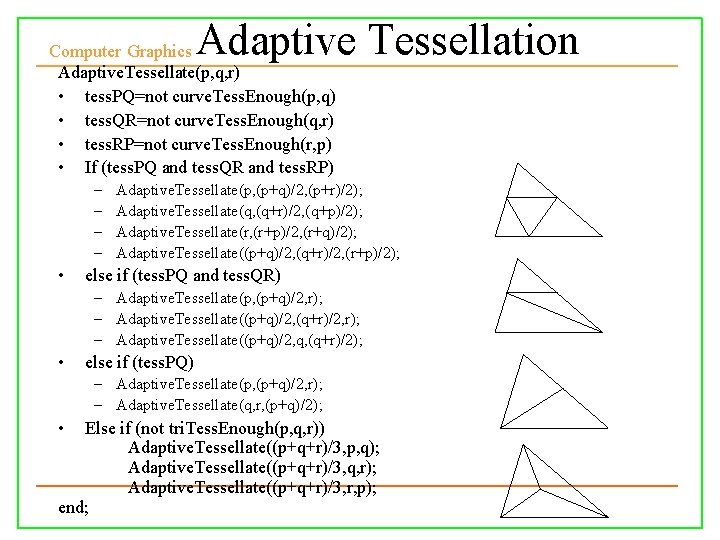
Computer Graphics Adaptive Tessellation • For every triangle edges, check if each edge is tessellated enough (curve. Tess. Enough()) • If all edges are tessellated enough, check if the whole triangle is tessellated enough as a whole (tri. Tess. Enough()) • If one or more of the edges or the triangle’s interior is not tessellated enough, then further tessellation is needed

Computer Graphics Adaptive Tessellation • When an edge is not tessellated enough, a point is created halfway between the edge points’ uv-values • New triangles are created and the tessellator is once again called with the new triangles as input Four cases of further tessellation

Adaptive Tessellation Computer Graphics Adaptive. Tessellate(p, q, r) • tess. PQ=not curve. Tess. Enough(p, q) • tess. QR=not curve. Tess. Enough(q, r) • tess. RP=not curve. Tess. Enough(r, p) • If (tess. PQ and tess. QR and tess. RP) – – • Adaptive. Tessellate(p, (p+q)/2, (p+r)/2); Adaptive. Tessellate(q, (q+r)/2, (q+p)/2); Adaptive. Tessellate(r, (r+p)/2, (r+q)/2); Adaptive. Tessellate((p+q)/2, (q+r)/2, (r+p)/2); else if (tess. PQ and tess. QR) – Adaptive. Tessellate(p, (p+q)/2, r); – Adaptive. Tessellate((p+q)/2, (q+r)/2, r); – Adaptive. Tessellate((p+q)/2, q, (q+r)/2); • else if (tess. PQ) – Adaptive. Tessellate(p, (p+q)/2, r); – Adaptive. Tessellate(q, r, (p+q)/2); • Else if (not tri. Tess. Enough(p, q, r)) Adaptive. Tessellate((p+q+r)/3, p, q); Adaptive. Tessellate((p+q+r)/3, q, r); Adaptive. Tessellate((p+q+r)/3, r, p); end;

Computer Graphics curve. Tess. Enough • Say you are to judge whether ab needs tessellation • You can compute the midpoint c, and compute its distance l from ab • Check if l/||a-b|| is under a threshold • Can do something similar for tri. Tess. Enough – Sample at the mass center and calculate its distance from the triangle c a d b

Computer Graphics Other factors to evaluate • • • Inside the view frustum Front facing Occupying a large area in screen space Close to the sillhouette of the object Illuminated by a significant amount of specular lighting

Computer Graphics Demo • http: //www. nbb. cornell. edu/neurobio/land/ Old. Student. Projects/cs 49096 to 97/anson/Bezier. Patch. Applet/

Computer Graphics Reading for this lecture • Foley et al. Chapter 11, section 11. 2 up to and including 11. 2. 3 • Introductory text Chapter 9, section 9. 2 up to and including section 9. 2. 4 • Foley at al. , Chapter 11, sections 11. 2. 3, 11. 2. 4, 11. 2. 9, 11. 2. 10, 11. 3 and 11. 5. • Introductory text, Chapter 9, sections 9. 2. 4, 9. 2. 5, 9. 2. 7, 9. 2. 8 and 9. 3. • Real-time Rendering 2 nd Edition Chapter 12. 1 -3 10/10/2008 Lecture 5 42