Computer Graphics Inf 4MSc Computer Graphics Lecture 7

Computer Graphics Inf 4/MSc Computer Graphics Lecture 7 Scanline algorithm and polygon clipping Taku Komura 1

Computer Graphics Inf 4/MSc Today’s topics • Scanline algorithm • Clipping

Computer Graphics Inf 4/MSc Scanline algorithm • Computing the barycentric coordinates for all the pixels inside the bounding box can be costly • We can try to scan only the pixels inside the polygon

Computer Graphics Inf 4/MSc Scanline algorithm For each scan line: 1. Find the intersections of the scan 　line with　all edges of the polygon. 2 Sort the intersections by increasing 　x coordinate. 3 Fill in all pixels between pairs of　 　intersections. Can also deal with concave polygons

Computer Graphics Span extrema Inf 4/MSc • Only turn on pixels whose centers are interior to the polygon: – Otherwise will intrude other adjacent polygons • round up values on the left edge of a span, round down on the right edge midpoint algorithm interior

Computer Graphics Edge Coherence Inf 4/MSc • Computing the intersections between scan lines and edges can be costly • Use a method similar to the midpoint algorithm • y = mx + b, x = (y – b) / m • At y = s, xs = (s – b ) / m At y = s + 1, xs+1 = (s+1 - b) / m = xs + 1 / m • Incremental calculation: xs+1 = xs + 1 / m

Inf 4/MSc Pseudo code of computing the left span extrema (m > 1) Computer Graphics

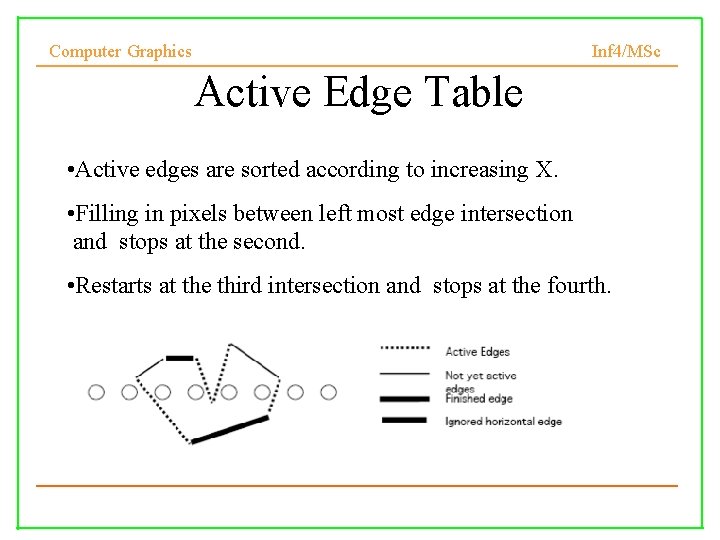
Computer Graphics Active Edge Table Inf 4/MSc • A table of edges that are currently used to fill the polygon • Scan lines are processed in increasing Y order. • Polygon edges are sorted according to their minimum Y. • When the current scan line reaches the lower endpoint of an edge it becomes active. • When the current scan line moves above the upper endpoint, the edge becomes inactive.

Computer Graphics Inf 4/MSc Active Edge Table • Active edges are sorted according to increasing X. • Filling in pixels between left most edge intersection and stops at the second. • Restarts at the third intersection and stops at the fourth.

Computer Graphics Polygon fill rules (to ensure consistency) Inf 4/MSc • Horizontal edges: Do not include in edge table • Vertices: If local max or min, then count twice, else count once. • If pixel is on edge, only draw left / bottom edges

Computer Graphics Inf 4/MSc Today’s topics • Scanline algorithm • Clipping

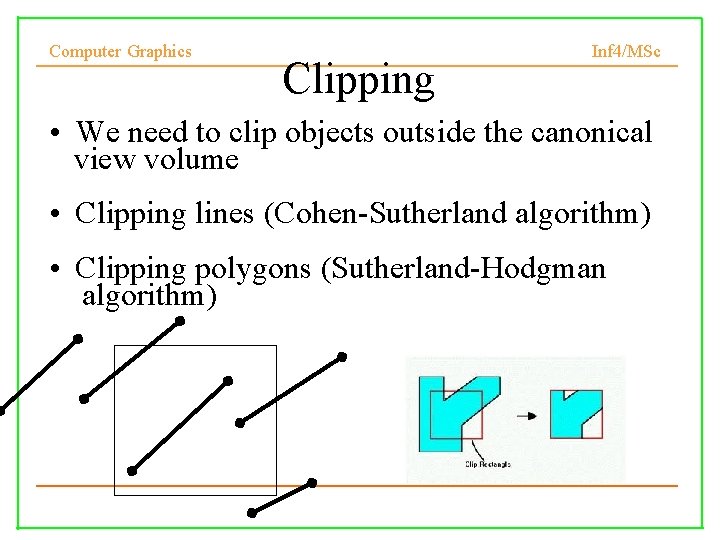
Computer Graphics Clipping Inf 4/MSc • We need to clip objects outside the canonical view volume • Clipping lines (Cohen-Sutherland algorithm) • Clipping polygons (Sutherland-Hodgman algorithm)

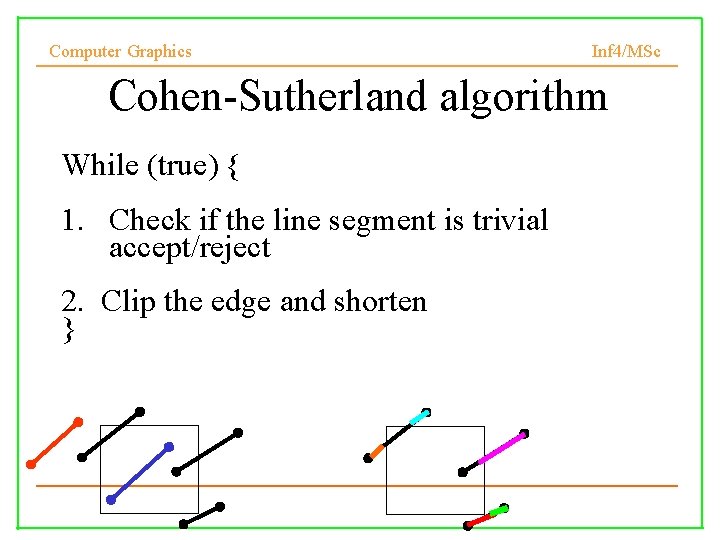
Computer Graphics Inf 4/MSc Cohen-Sutherland algorithm While (true) { 1. Check if the line segment is trivial accept/reject 2. Clip the edge and shorten }

Computer Graphics Inf 4/MSc What is a trivial accept / reject? • Trivial acceptance All line vertices lie inside box accept.

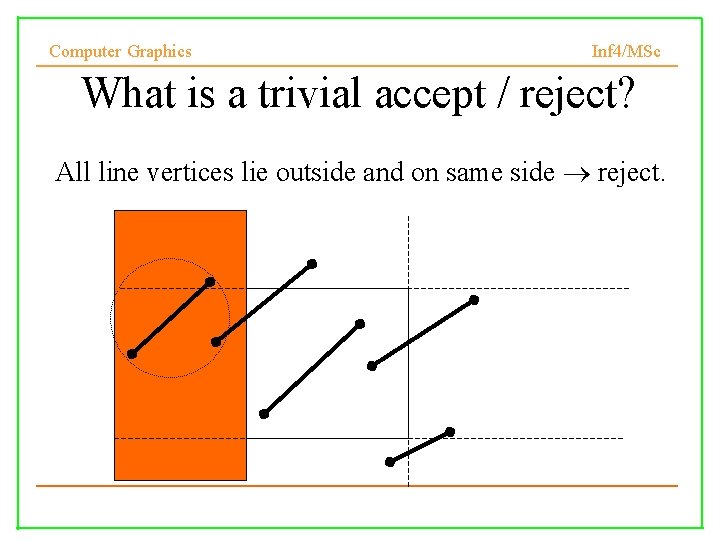
Computer Graphics Inf 4/MSc What is a trivial accept / reject? All line vertices lie outside and on same side reject.

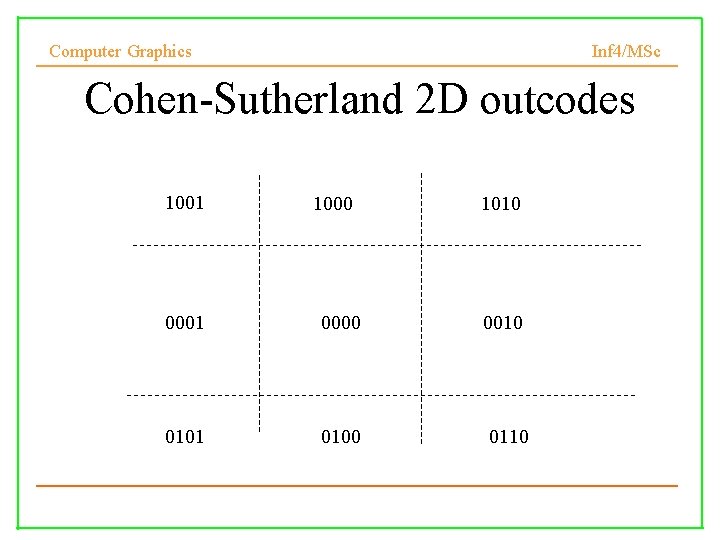
Computer Graphics Inf 4/MSc Cohen-Sutherland 2 D outcodes – 4 -bit code called: Outcode – First bit : above top of window, y > ymax – Second bit : below bottom, y < ymin – Third bit : to right of right edge, x > xmax – Fourth bit : to left of left edge, x < xmin

Computer Graphics Inf 4/MSc Cohen-Sutherland 2 D outcodes 1001 1000 1010 0001 0000 0010 0101 0100 0110

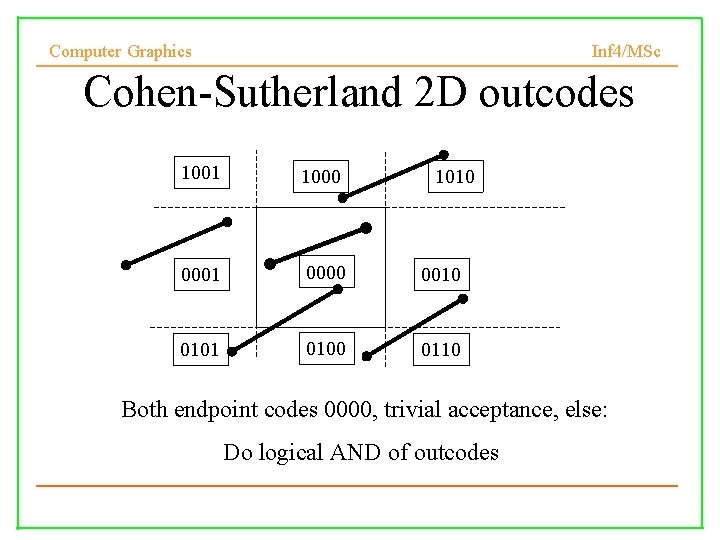
Computer Graphics Inf 4/MSc Cohen-Sutherland 2 D outcodes 1001 1000 0001 0000 0010 0101 0100 0110 1010 Both endpoint codes 0000, trivial acceptance, else: Do logical AND of outcodes

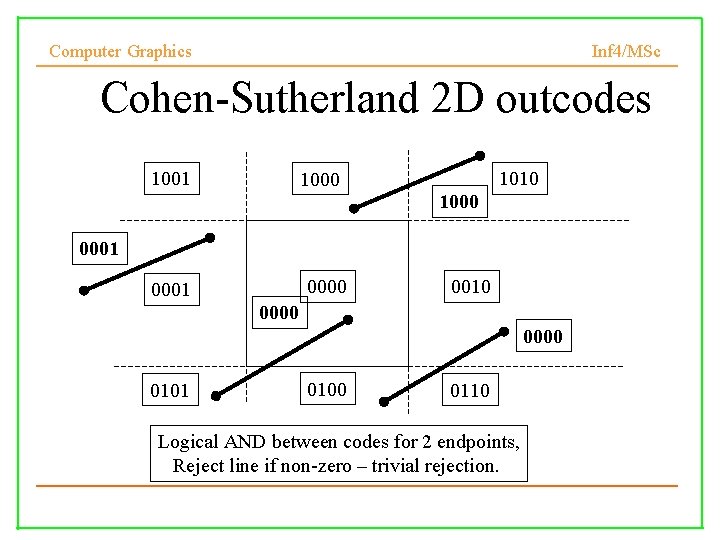
Computer Graphics Inf 4/MSc Cohen-Sutherland 2 D outcodes 1001 1010 1000 0001 0000 0001 0010 0000 0101 0100 0110 Logical AND between codes for 2 endpoints, Reject line if non-zero – trivial rejection.

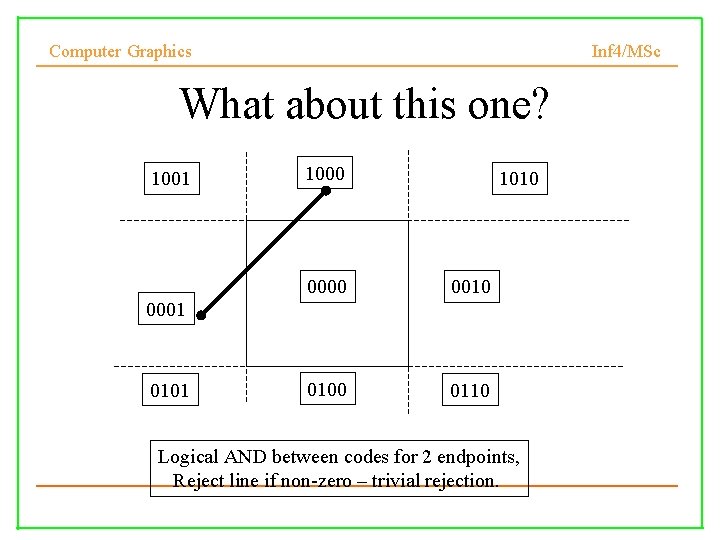
Computer Graphics Inf 4/MSc What about this one? 1001 1000 1010 0000 0010 0100 0110 0001 0101 Logical AND between codes for 2 endpoints, Reject line if non-zero – trivial rejection.

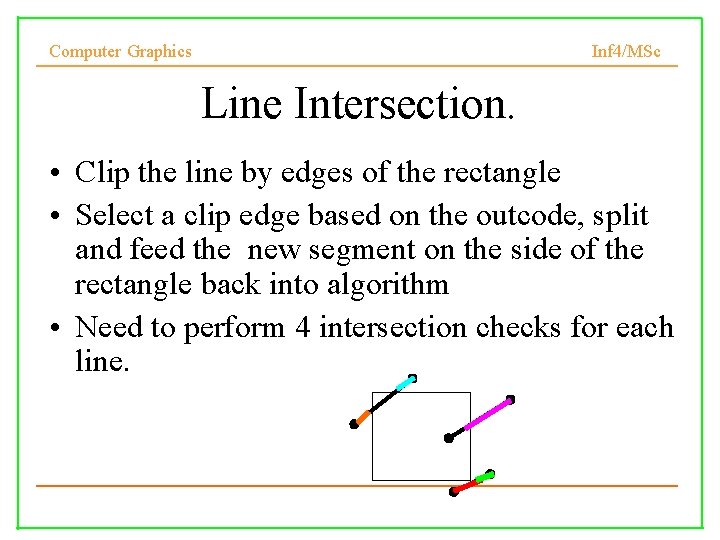
Computer Graphics Inf 4/MSc Line Intersection. • Clip the line by edges of the rectangle • Select a clip edge based on the outcode, split and feed the new segment on the side of the rectangle back into algorithm • Need to perform 4 intersection checks for each line.

Computer Graphics Inf 4/MSc Polygon Clipping • Sutherland-Hodgman’s algorithm • Polygons are clipped at each edge of the window while traversing the polygon • Output : a list of vertices of the clipped polygon

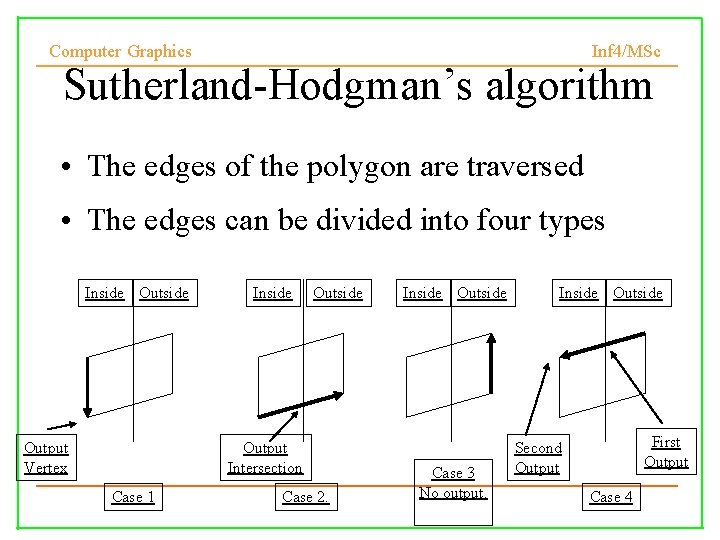
Computer Graphics Inf 4/MSc Sutherland-Hodgman’s algorithm • The edges of the polygon are traversed • The edges can be divided into four types Inside Output Vertex Inside Output Intersection Case 1 Case 2. Inside Outside Case 3 No output. Inside Outside First Output Second Output Case 4

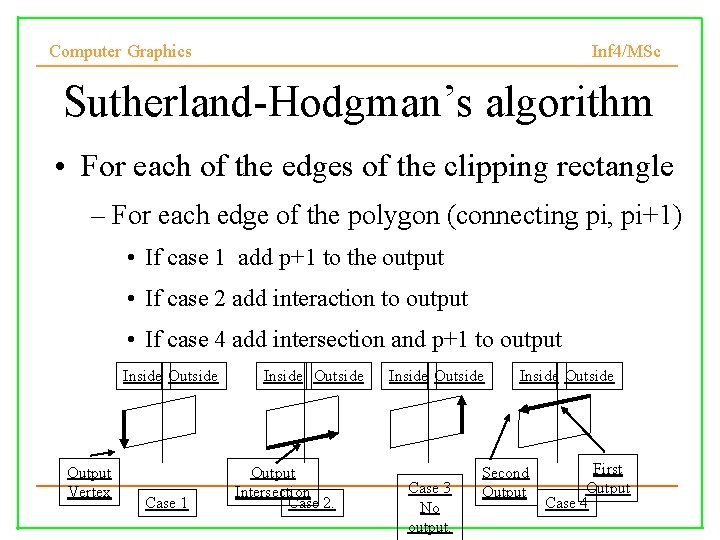
Computer Graphics Inf 4/MSc Sutherland-Hodgman’s algorithm • For each of the edges of the clipping rectangle – For each edge of the polygon (connecting pi, pi+1) • If case 1 add p+1 to the output • If case 2 add interaction to output • If case 4 add intersection and p+1 to output Inside Output Vertex Case 1 Inside Output Intersection Case 2. Inside Outside Case 3 No output. Inside Outside Second Output First Output Case 4

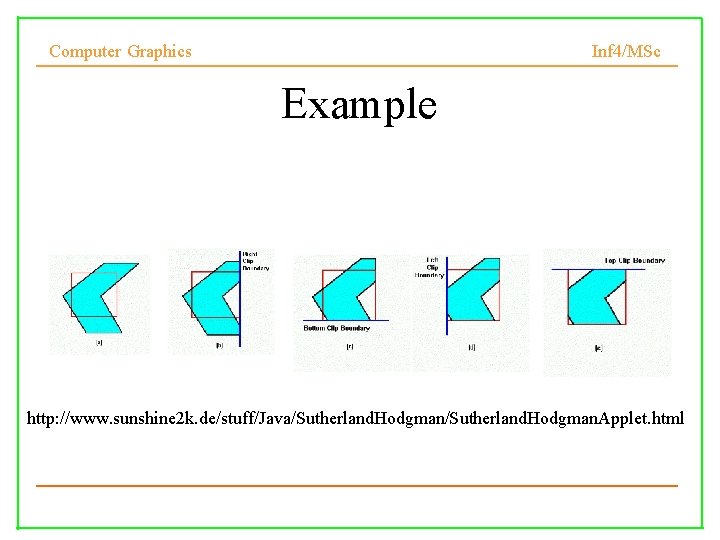
Computer Graphics Inf 4/MSc Example http: //www. sunshine 2 k. de/stuff/Java/Sutherland. Hodgman. Applet. html

Computer Graphics Inf 4/MSc References • Scanline algorithm Foley et al. , Chapter 3. 5, 3. 6 • Clipping lines, polygons – Foley et al. Chapter 3. 12, 3. 14 – http: //www. cc. gatech. edu/grads/h/Haowei. Hsieh/mm. html 26