Computer Graphics I Basic Modelling 1 Lecture Objectives

Computer Graphics I Basic Modelling 1

Lecture Objectives To understand how 3 D scenes can be modelled - in terms of geometry, appearance and behaviour - and rendered on a display n To understand how to deliver interactive animated 3 D graphics over the Internet n To be able to create interactive 3 D graphics applications using industry standard software (Open. GL and VRML) n 2

The Basics n MODELLING – representing objects in 3 D – transforming objects and composing scenes n VIEWING – projecting 3 D scenes onto a 2 D display surface n RENDERING – illumination – shading – adding realism via textures, shadows 3

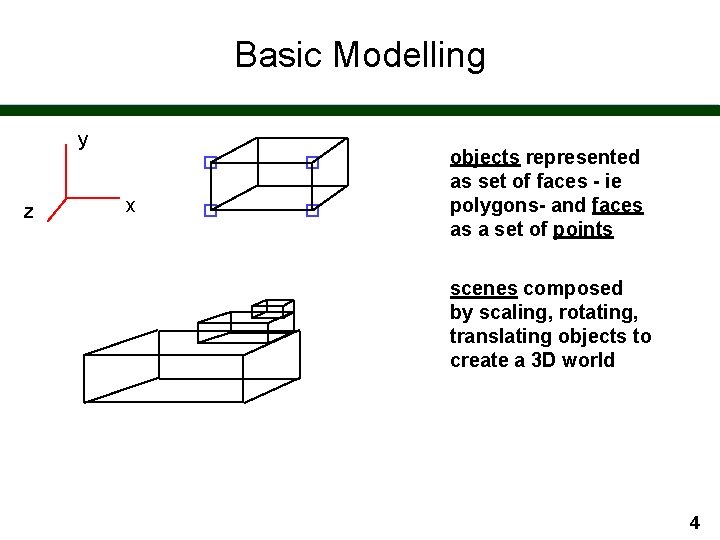
Basic Modelling y z x objects represented as set of faces - ie polygons- and faces as a set of points scenes composed by scaling, rotating, translating objects to create a 3 D world 4

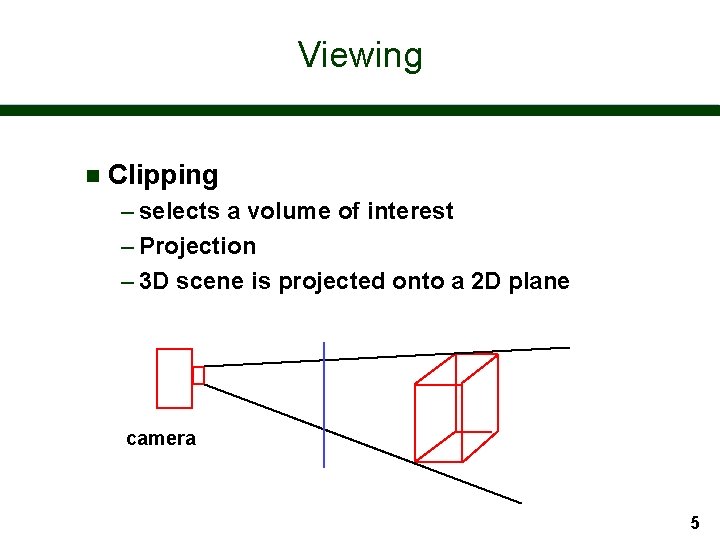
Viewing n Clipping – selects a volume of interest – Projection – 3 D scene is projected onto a 2 D plane camera 5

Rendering illumination: how is light reflected from surfaces? shading: how do we use our knowledge of illumination to shade surfaces in our world? 6

Rendering n texture n shadows 7

Internet n VRML – ISO standard for 3 D graphics over the Web – allows modelling of geometry, appearance and behaviour 8

Advanced Rendering n ADVANCED RENDERING – direct versus global illumination methods – ray tracing and radiosity n OTHER ADVANCED FEATURES – curve and surface modelling – image based rendering – non-photorealistic rendering 9

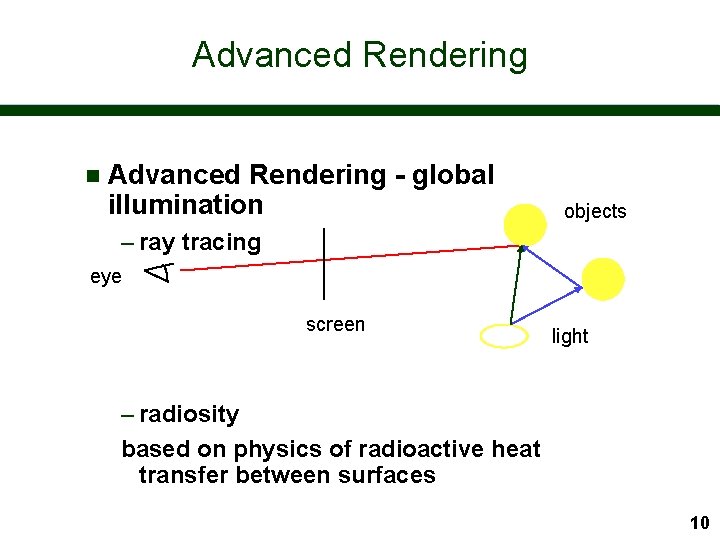
Advanced Rendering n Advanced Rendering - global illumination objects – ray tracing eye screen light – radiosity based on physics of radioactive heat transfer between surfaces 10

Ray Tracing 11

Radiosity 12

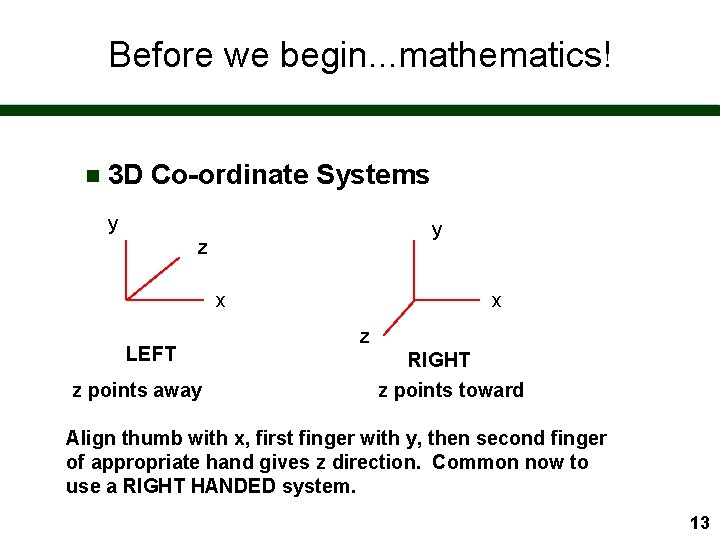
Before we begin. . . mathematics! n 3 D Co-ordinate Systems y y z x LEFT z points away x z RIGHT z points toward Align thumb with x, first finger with y, then second finger of appropriate hand gives z direction. Common now to use a RIGHT HANDED system. 13

Points and Vectors n We shall write points as column vectors y P = x y z P x z Difference of two points gives a direction vector: D = P 2 - P 1 y P 2 z x P 1 Note: If P 1 and P 2 are on a plane, then D lies in the plane 14

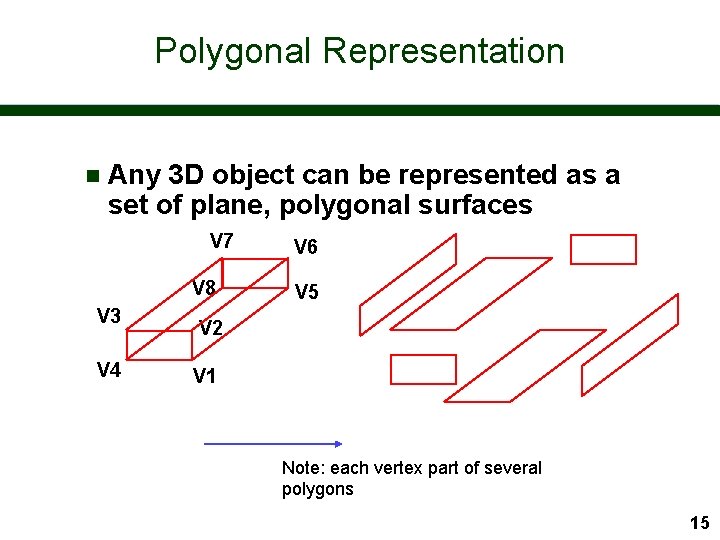
Polygonal Representation n Any 3 D object can be represented as a set of plane, polygonal surfaces V 7 V 8 V 3 V 4 V 6 V 5 V 2 V 1 Note: each vertex part of several polygons 15

Polygonal Representation n Objects with curved surfaces can be approximated by polygons - improved approximation by more polygons 16

Scene Organisation Scene = list of objects n Object = list of surfaces n Surface = list of polygons n Polygon = list of vertices n scene vertices object surfaces polygons 17

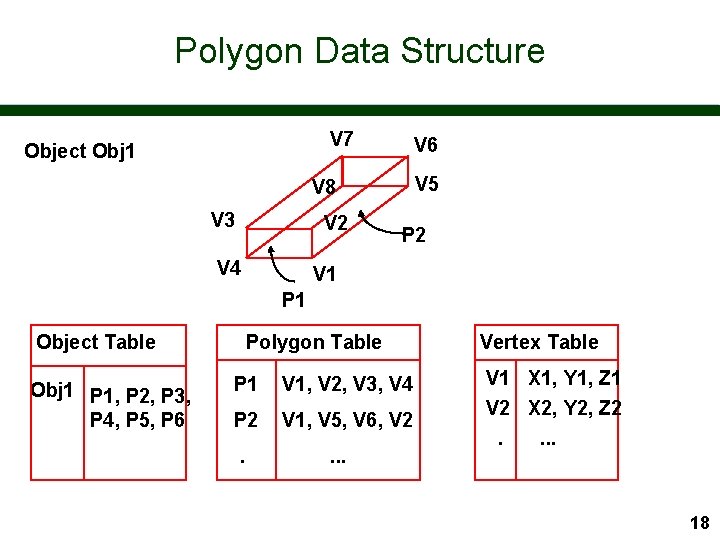
Polygon Data Structure V 7 Object Obj 1 V 6 V 5 V 8 V 3 V 2 V 4 P 2 V 1 P 1 Object Table Obj 1 P 1, P 2, P 3, P 4, P 5, P 6 Polygon Table P 1 V 1, V 2, V 3, V 4 P 2 V 1, V 5, V 6, V 2 . . Vertex Table V 1 X 1, Y 1, Z 1 V 2 X 2, Y 2, Z 2. . 18

Typical Primitives n Graphics systems such as Open. GL typically support: – triangles, triangle strips and fans – quads, quad strips – polygons n Which way is front? – convention is that normal points towards you if vertices are specified counterclockwise 19

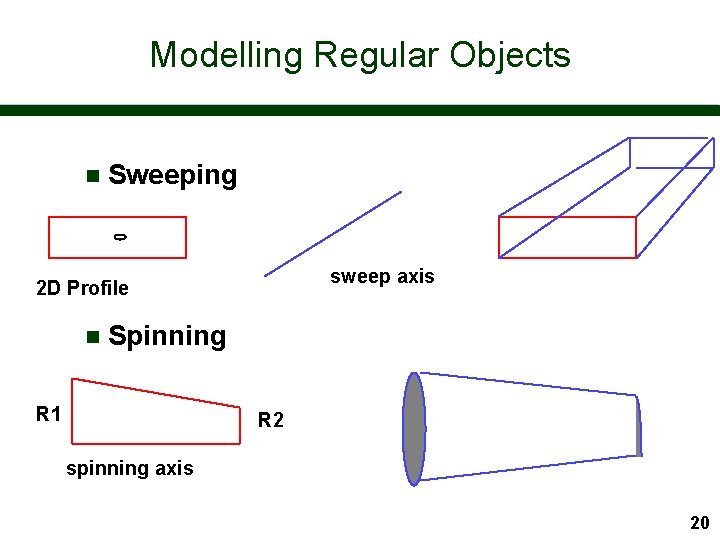
Modelling Regular Objects n Sweeping sweep axis 2 D Profile n Spinning R 1 R 2 spinning axis 20

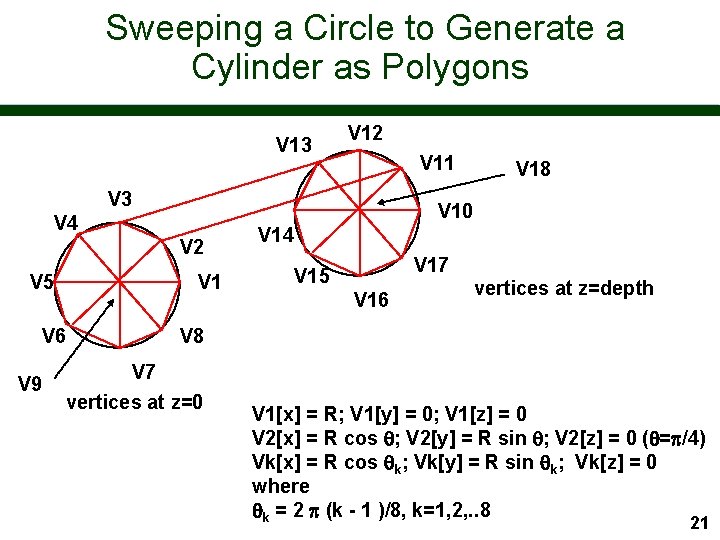
Sweeping a Circle to Generate a Cylinder as Polygons V 13 V 12 V 11 V 3 V 10 V 4 V 2 V 5 V 1 V 6 V 9 V 18 V 14 V 17 V 15 V 16 vertices at z=depth V 8 V 7 vertices at z=0 V 1[x] = R; V 1[y] = 0; V 1[z] = 0 V 2[x] = R cos ; V 2[y] = R sin ; V 2[z] = 0 ( =p/4) Vk[x] = R cos k; Vk[y] = R sin k; Vk[z] = 0 where k = 2 p (k - 1 )/8, k=1, 2, . . 8 21

Complex Primitives n Some systems such as VRML have cylinders, cones, etc as primitives – polygonal representation calculated automatically n Open. GL has a utility library (GLU) which contains various high-level primitives – again converted to polygons n For conventional graphics hardware: – POLYGONS RULE! 22

Automatic Generation of Polygonal Objects n 3 D scanners - or laser rangers - are able to generate computer representations of objects – object sits on rotating table – contour outline generated for a given height – scanner moves up a level and next contour created – successive contours stitched together to give polygonal representation 23

A Puzzle 24

Modelling Objects and Creating Worlds We have seen how boundary representations of simple objects can be created n Typically each object is created in its own co-ordinate system n To create a world, we need to understand how to transform objects so as to place them in the right place translation, translation at the right size - scaling, scaling in the right orientation- rotation n 25

Transformations n The basic linear transformations are: – translation: P = P + T, where T is translation vector – scaling: P’ = S P, where S is a scaling matrix – rotation: P’ = R P, where R is a rotation matrix n As in 2 D graphics, we use homogeneous co-ordinates in order to express all transformations as matrices and allow them to be combined easily 26

Homogeneous Co-ordinates In homogeneous coordinates, a 3 D point P = (x, y, z)T is represented as: P = (x, y, z, 1)T n That is, a point in 4 D space, with its ‘extra’ co-ordinate equal to 1 n Note: Note in homogeneous co-ordinates, multiplication by a constant leaves point unchanged n – ie (x, y, z, 1)T = (wx, wy, wz, w)T 27

Translation Suppose we want to translate P (x, y, z)T by a distance (Tx, Ty, Tz)T n We express P as (x, y, z, 1)T and form a translation matrix T as below n The translated point is P’ n x’ y’ z’ 1 = P’ = 1 0 0 0 0 1 0 T Tx Ty Tz 1 x y z 1 P = x + Tx y + Ty z + Tz 1 28

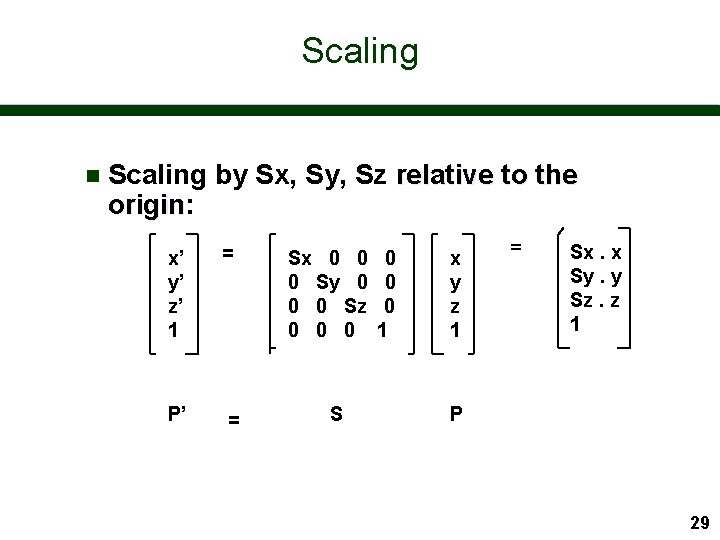
Scaling n Scaling by Sx, Sy, Sz relative to the origin: origin x’ y’ z’ 1 = P’ = Sx 0 0 0 Sy 0 0 0 Sz 0 0 0 S 0 0 0 1 x y z 1 = Sx. x Sy. y Sz. z 1 P 29

Rotation is specified with respect to an axis - easiest to start with co-ordinate axes n To rotate about the x-axis: n x’ y’ z’ 1 = P’ = 1 0 0 cos -sin 0 0 sin cos 0 0 1 Rz ( ) x y z 1 P a positive angle corresponds to counter-clockwise direction looking at origin from positive position on axis 30

Composite Transformations The attraction of homogeneous co-ordinates is that a sequence of transformations may be encapsulated as a single matrix n For example, scaling with respect to a fixed position (a, b, c) can be achieved by: n – translate fixed point to origin- say, T(-a, -b, -c) – scale- S – translate fixed point back to its starting position. T(a, b, c) n Thus: P’ = T(a, b, c) S T(-a, -b, -c) P = M P 31

Rotation about a Specified Axis It is useful to be able to rotate about any axis in 3 D space n This is achieved by composing 7 elementary transformations n 32

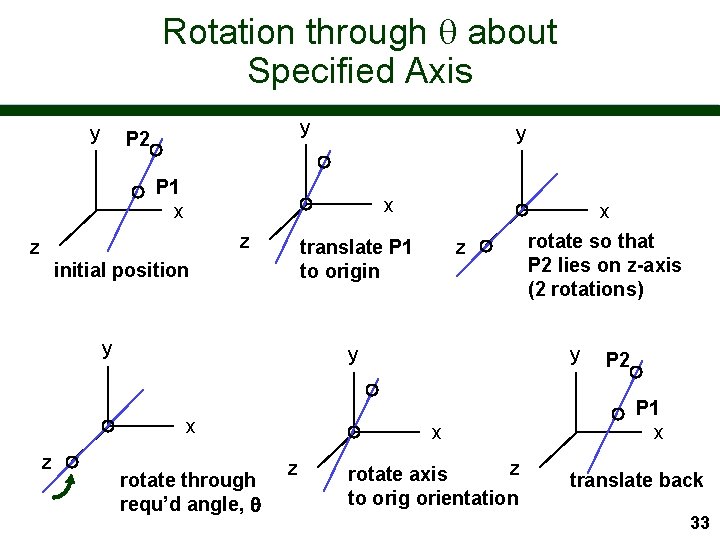
Rotation through about Specified Axis y y P 2 y P 1 x x z z translate P 1 to origin initial position y y x z z rotate through requ’d angle, y x z x rotate so that P 2 lies on z-axis (2 rotations) z rotate axis to orig orientation P 2 P 1 x translate back 33

Inverse Transformations n As in this example, it is often useful to calculate the inverse of a transformation – ie the transformation that returns to original state Translation: T-1 (a, b, c) = T (-a, -b, -c) n Scaling: S-1 ( Sx, Sy, Sz ) = S. . . n Rotation: R-1 z ( ) = Rz (- ) n 34

Computer Graphics I Viewing - Projections 35

Viewing Graphics display devices are 2 D rectangular screens n Hence we need to understand how to transform our 3 D world to a 2 D surface n This involves: n – selecting the observer position (or camera position) – selecting the view plane (or camera film plane) – selecting the type of projection 36

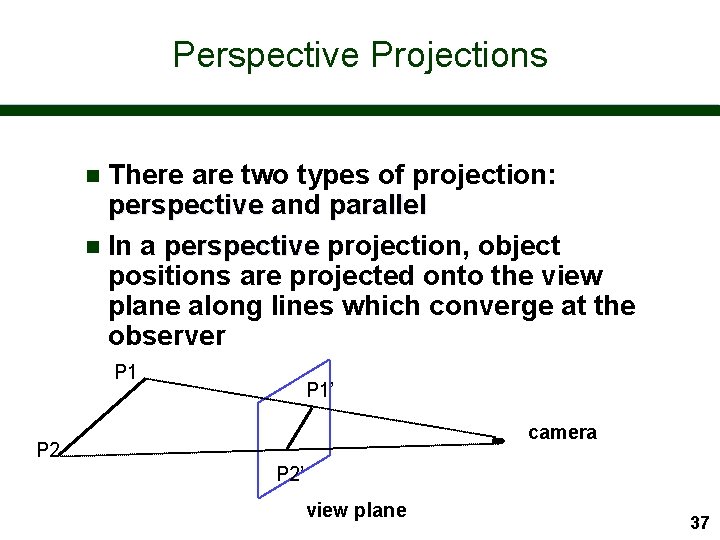
Perspective Projections There are two types of projection: perspective and parallel n In a perspective projection, object positions are projected onto the view plane along lines which converge at the observer n P 1’ camera P 2’ view plane 37

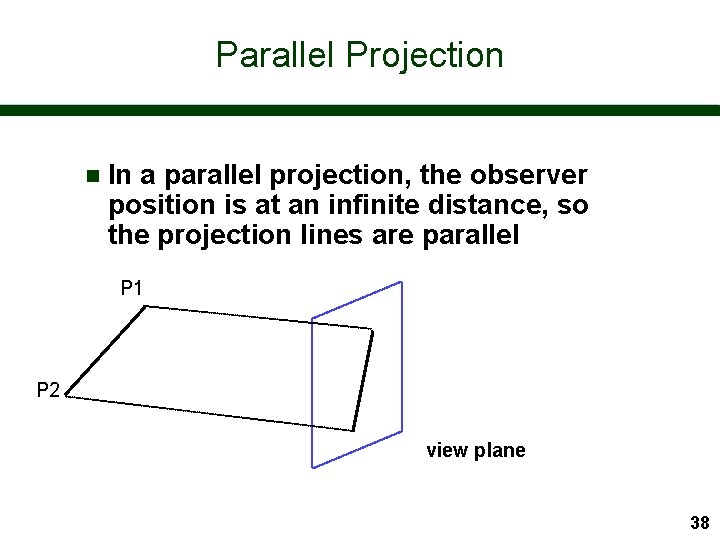
Parallel Projection n In a parallel projection, the observer position is at an infinite distance, so the projection lines are parallel P 1 P 2 view plane 38

Perspective and Parallel Projection Parallel projection preserves the relative proportions of objects, but does not give a realistic view n Perspective projection gives realistic views, but does not preserve proportions n – Projections of distant objects are smaller than projections of objects of the same size which are closer to the view plane 39

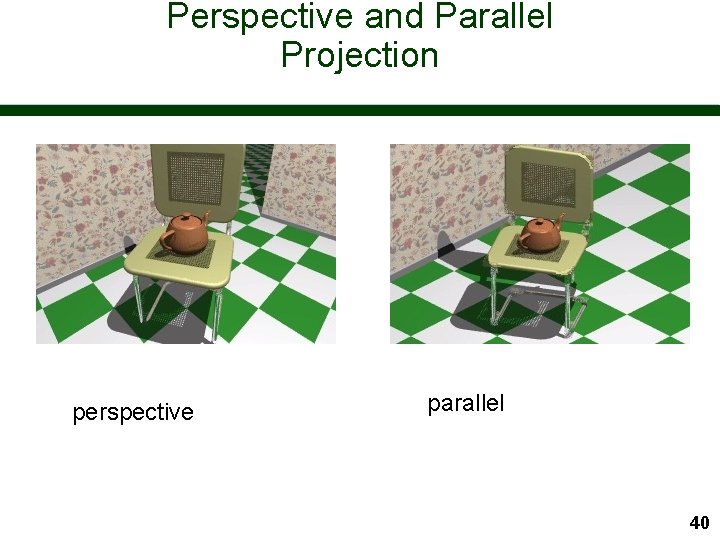
Perspective and Parallel Projection perspective parallel 40

Puzzle 41

Another Example 42

Viewing Coordinate System n Viewing is easier if we work in a viewing co-ordinate system, system where the observer or camera position is on the z -axis, looking along the negative zdirection y. V x. V z. V Camera is positioned at: (0 , 0, z. C) 43

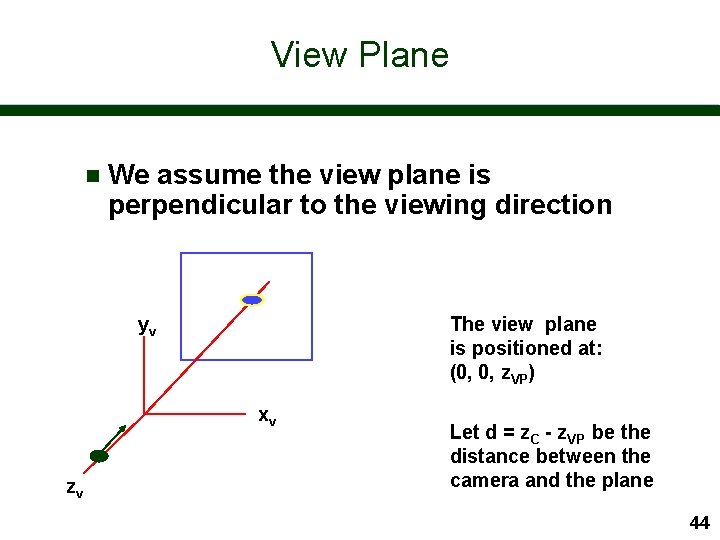
View Plane n We assume the view plane is perpendicular to the viewing direction yv The view plane is positioned at: (0, 0, z. VP) xv zv Let d = z. C - z. VP be the distance between the camera and the plane 44

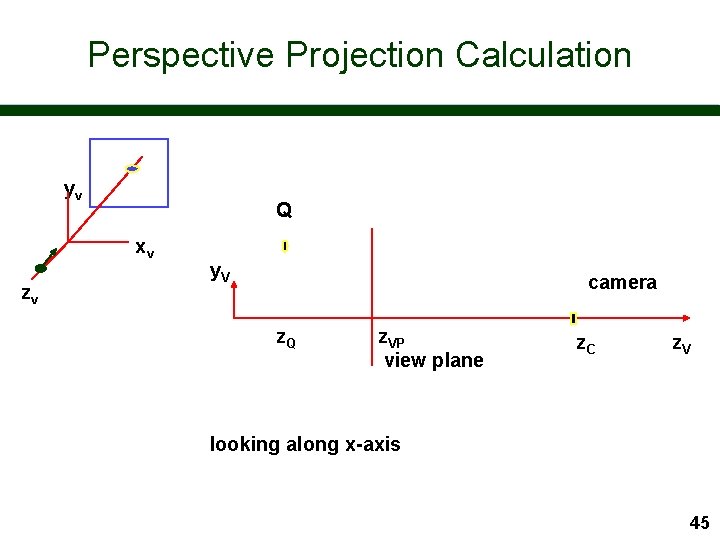
Perspective Projection Calculation yv Q xv zv y. V camera z. Q z. VP view plane z. C z. V looking along x-axis 45

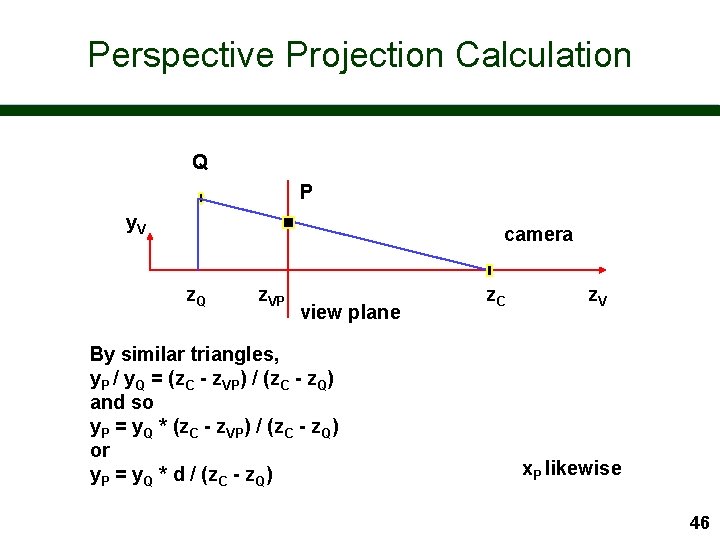
Perspective Projection Calculation Q P y. V camera z. Q z. VP view plane By similar triangles, y. P / y. Q = (z. C - z. VP) / (z. C - z. Q) and so y. P = y. Q * (z. C - z. VP) / (z. C - z. Q) or y. P = y. Q * d / (z. C - z. Q) z. C z. V x. P likewise 46

Transformation Matrix for Perspective 1 0 0 0 x. Q y. H 0 1 0 0 y. Q z. H 0 0 -z. VP/d z. VPz. C/d z. Q w. H 0 0 -1/d 1 x. H = Then x. P = x. H / w. H ie x. P = x. H / ( (z. C - z. Q) / d ) ie x. P = x. Q / ( (z. C - z. Q) / d ) z. C/d y. P likewise 47

Note for Later n The original z co-ordinate of points is retained – we need relative depth in the scene in order to sort out which faces are visible to the camera 48

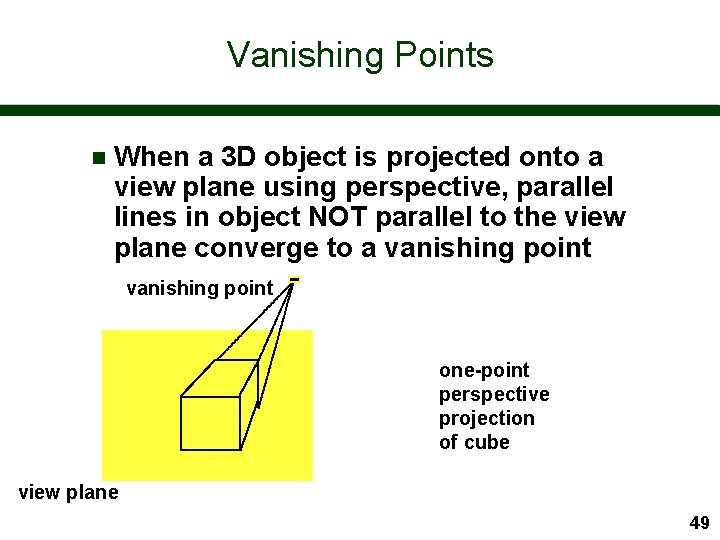
Vanishing Points n When a 3 D object is projected onto a view plane using perspective, parallel lines in object NOT parallel to the view plane converge to a vanishing point one-point perspective projection of cube view plane 49

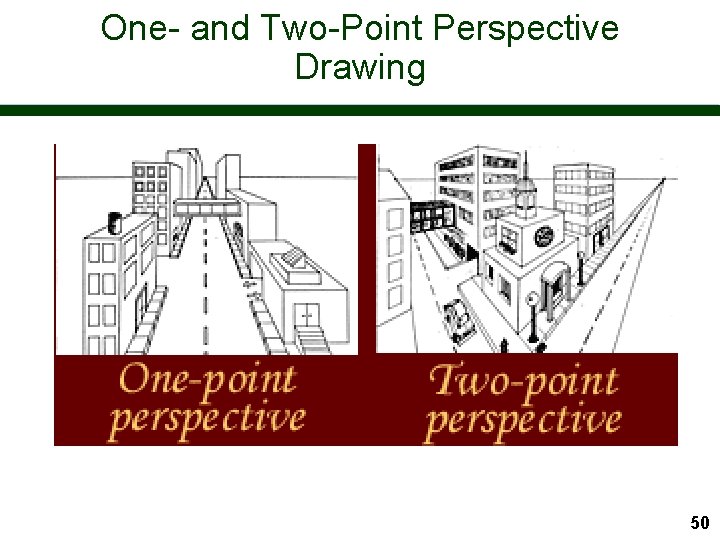
One- and Two-Point Perspective Drawing 50

One-point Perspective This is: Trinity with the Virgin, St John and Donors, by Mastaccio in 1427 Said to be the first painting in perspective 51

Two-point Perspective Edward Hopper Lighthouse at Two Lights -see www. postershop. com 52

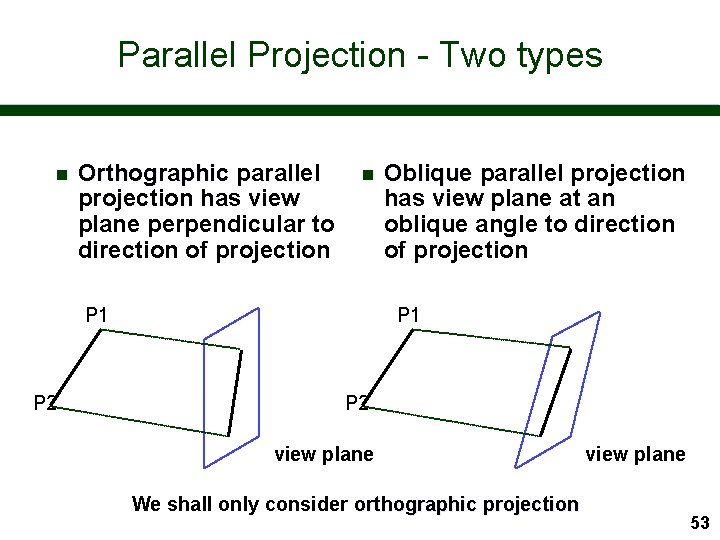
Parallel Projection - Two types n Orthographic parallel projection has view plane perpendicular to direction of projection n P 1 P 2 Oblique parallel projection has view plane at an oblique angle to direction of projection P 1 P 2 view plane We shall only consider orthographic projection view plane 53

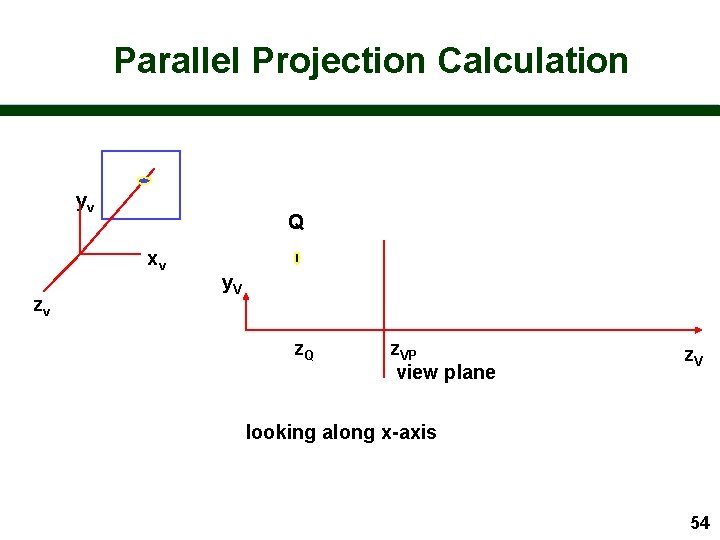
Parallel Projection Calculation yv Q xv zv y. V z. Q z. VP view plane z. V looking along x-axis 54

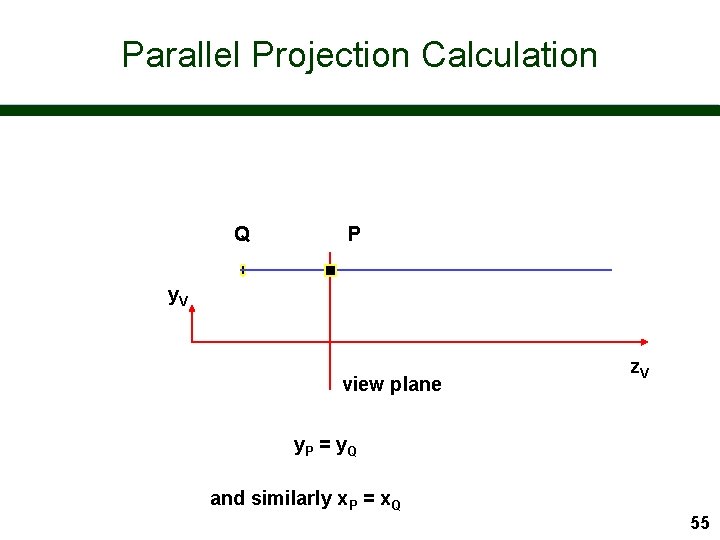
Parallel Projection Calculation Q P y. V view plane z. V y. P = y Q and similarly x. P = x. Q 55

Parallel Projection Calculation n So this is much easier than perspective! – x. P = x Q – y. P = y Q – z. P = z. VP n The transformation matrix is simply 1 0 0 0 z. VP/z. Q 0 0 1 56

View Volumes - View Window n Type of lens in a camera is one factor which determines how much of the view is captured – wide angle lens captures more than regular lens n Analogy in computer graphics is the view window, window a rectangle in the view plane view window yv xv zv 57

View Volume - Front and Back Planes We will also typically want to limit the view in the z. V direction n We define two planes, each parallel to the view plane, to achieve this n – front plane (or near plane) – back plane (or far plane) z. V back plane front plane 58

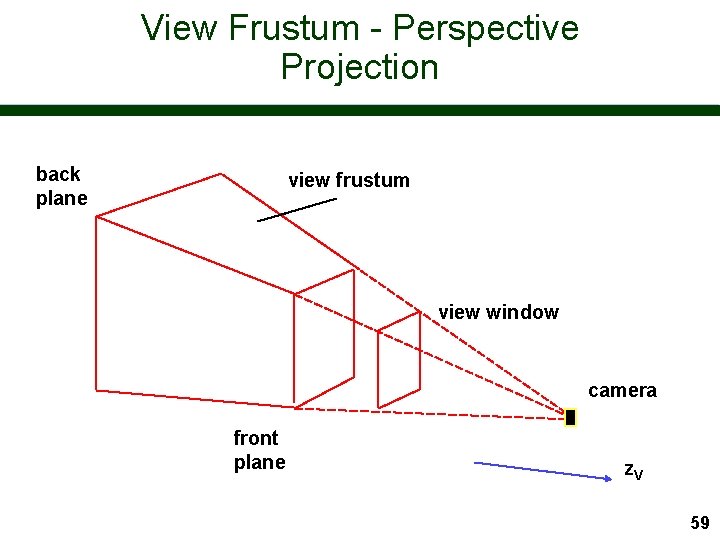
View Frustum - Perspective Projection back plane view frustum view window camera front plane z. V 59

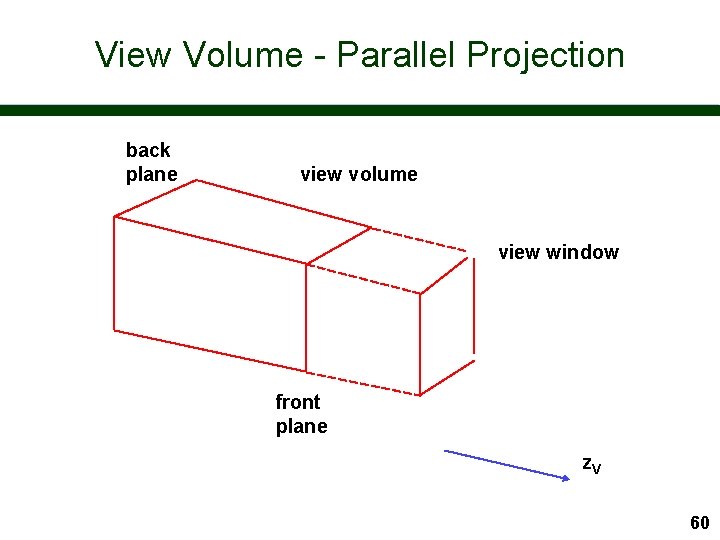
View Volume - Parallel Projection back plane view volume view window front plane z. V 60

View Volume The front and back planes act as important clipping planes n Can be used to select part of a scene we want to view n Front plane important in perspective to remove near objects which will swamp picture n 61

Computer Graphics I VRML - An Introduction 62

Good Ideas are Simple n Realization 1: – Hypertext + Internet = World Wide Web n Realization 2: – Adding images makes pages more interesting n Realization 3: – Images are pictures taken by the publisher why not send 3 D scenes and allow the user to take the picture! n VRML: Virtual Reality Modelling Language – a language to describe 3 D worlds - for the Web 63

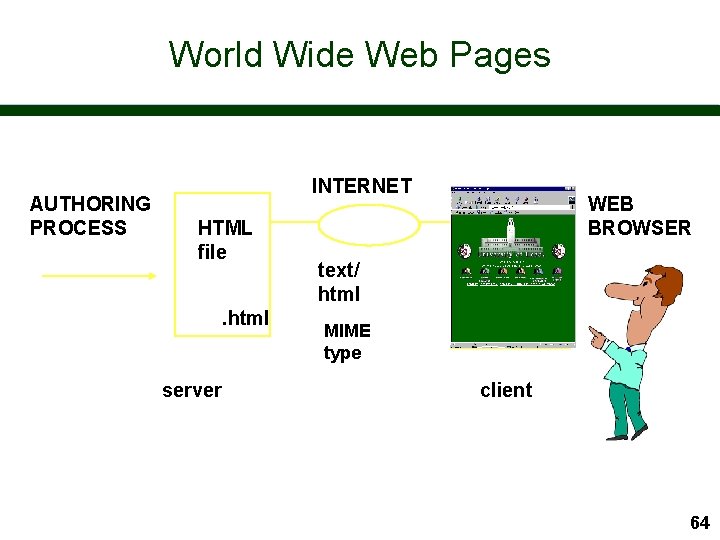
World Wide Web Pages AUTHORING PROCESS INTERNET HTML file. html server WEB BROWSER text/ html MIME type client 64

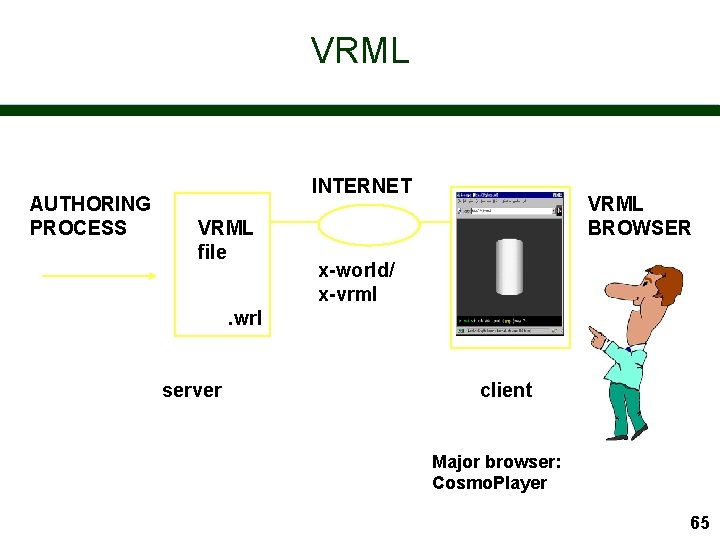
VRML AUTHORING PROCESS INTERNET VRML file VRML BROWSER x-world/ x-vrml . wrl server client Major browser: Cosmo. Player 65

Advantages of VRML n Transferring a 3 D model - rather than a 2 D image - to the browser has great advantages – viewer can choose how to look at the model - or world – viewer can navigate the world – file size can often be much less 66

How Did It All Begin? n Original brainwave – Mark Pesce and Tony Parisi - early 1994 – vision of a VR interface to the Web n VRML 1. 0 – practical realisation based on Open Inventor (Silicon Graphics toolkit - similar to Open. GL but higher level) – Open Inventor file format PLUS hyperlinks – static, non-interactive worlds – Gavin Bell (SGI) - late 1994 67

Where are we now? n VRML 97 – adds object behaviours and interaction to allow creation of dynamic worlds – ISO standard - December 1997 – Gavin Bell, Rikk Carey (ex-SGI) and Chris Marrin (SGI) n 2000 – being reworked as XML (X 3 D) – many new developments 68

A VRML File VRML file consists of: n header n nodes – objects such as cylinders and spheres – operations such as transformations n fields – parameters of nodes #VRML V 2. 0 utf 8 Shape { geometry Cylinder { radius 3 height 6 } } 69

As Seen By A Browser #VRML V 2. 0 utf 8 Shape { geometry Cylinder { radius 2 height 4 } } 70

Adding Color to the Scene #VRML V 2. 0 utf 8 Shape { geometry Cylinder { radius 2 height 4 } appearance Appearance { material Material { diffuse. Color 1 0 0 specular. Color 1 1 1 } } } 71

Co-ordinate Systems n Each node is drawn within its own local co-ordinate system. . y x z 72

Modelling Transformations n n n . . . and can be subjected to a modelling transformation to scale, rotate, translate Transform is a VRML node - treated just like an object It applies to a group of children nodes #VRML V 2. 0 utf 8 Transform{ scale 5. 0 0. 5 1. 0 children [ Shape { geometry Cylinder { radius 2 height 4 } appearance Appearance { material Material { diffuse. Color 1 0 0 specular. Color 1 1 1 } }}]} 73

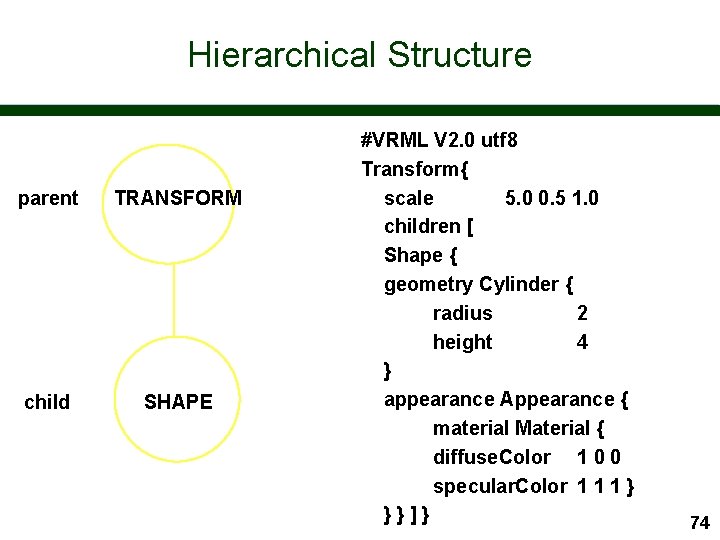
Hierarchical Structure parent TRANSFORM child SHAPE #VRML V 2. 0 utf 8 Transform{ scale 5. 0 0. 5 1. 0 children [ Shape { geometry Cylinder { radius 2 height 4 } appearance Appearance { material Material { diffuse. Color 1 0 0 specular. Color 1 1 1 } }}]} 74

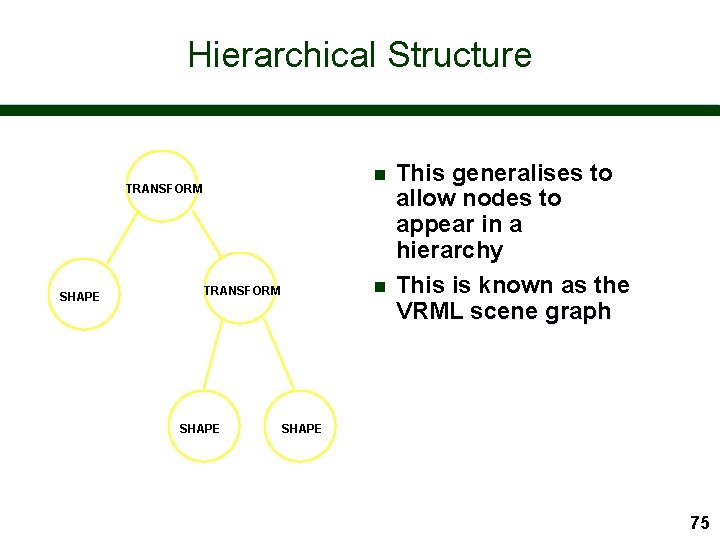
Hierarchical Structure n TRANSFORM SHAPE This generalises to allow nodes to appear in a hierarchy This is known as the VRML scene graph SHAPE 75

Transformations n n Here we see Cylinder, Sphere and Cone nodes Each has been subjected to a modelling transformation in order to position them 76

Instances n n n A node can be given a ‘name’ and then used multiple times with different transformations applied to each DEF kwb Shape {. . . } gives it a name USE kwb allows it to be included at other points in the scene graph 77

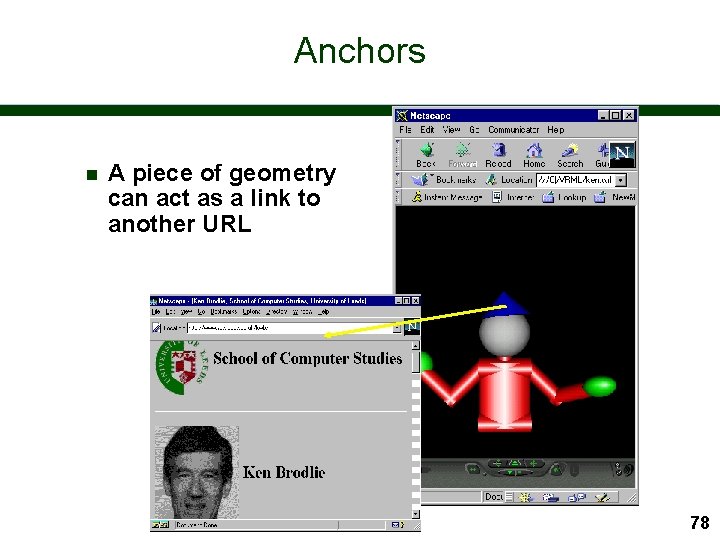
Anchors n A piece of geometry can act as a link to another URL 78

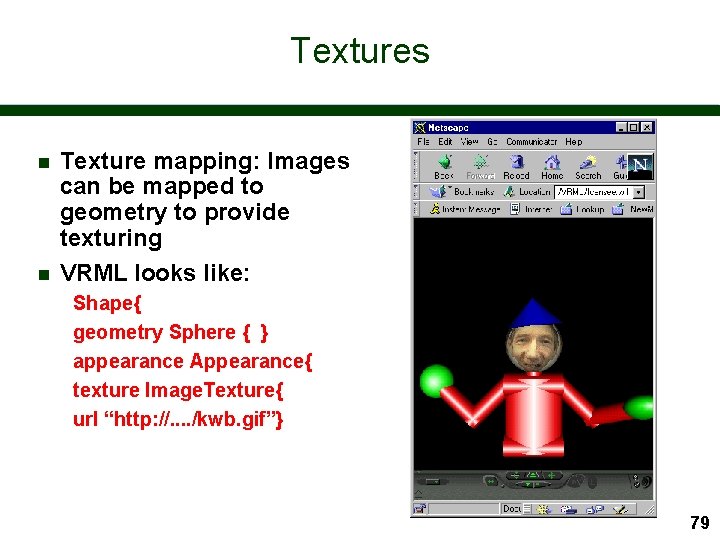
Textures n n Texture mapping: Images can be mapped to geometry to provide texturing VRML looks like: Shape{ geometry Sphere { } appearance Appearance{ texture Image. Texture{ url “http: //. . /kwb. gif”} 79

Polygonal Surfaces n The general primitive for drawing polygonal surfaces is: – Indexed. Face. Set – coord field lists the points – coord. Index describes the polygons Shape{ geometry Indexed. Face. Set { coord Coordinate { point [ 17. 5 11. 2 -1. 2, 17. 5 15. 0 -1. 2, …] } coord. Index [ 0 1 2 3 -1, 4 1 0 5 -1, …] } } 80

Lights n VRML includes: – Directional. Light – Point. Light – Spot. Light n Note # sign is a comment Example: Point. Light{ on intensity color location radius } TRUE 0. 75 1 0 0 #red 000 100 81

Viewing n n n Specified via the Viewpoint node VRML file can have a number of Viewpoint nodes - browsers allow a user to jump from one viewpoint to another Orientation = axis + angle of rotation Example: Viewpoint { position orientation description } 005 0 0 1 0. 3 “frontview” 82

Other Basic Features n Inline node – incorporate VRML code from another url – this allows us to compose large worlds from many smaller ones n Level of Detail – different geometric representations depending on distance 83

Information About VRML n Web 3 D Consortium – http: //www. web 3 d. org – links to specifications and resources n Web 3 D Information – http: //web 3 d. about. com/compute/web 3 d n Leeds University VRML/Java 3 D Information Centre – http: //www. scs. leeds. ac. uk/vrmljava 3 d n VRML Repository – http: //www. sdsc. edu/vrml/ 84

Books and Tutorials n Range of books now available – The VRML 2. 0 Handbook (Addison Wesley) Jed Hartman and Josie Wernecke http: //vrml. sgi. com/handbook – The Annotated VRML Reference Book (Addison Wesley) Rikk Carey and Gavin Bell http: //www. best. com/~rikk/Book/ n Tutorials include: – Floppy’s guide: www. vapourtech. com/vrmlguide 85