Computer Graphics Chapter 5 Vector Based Algorithms 1

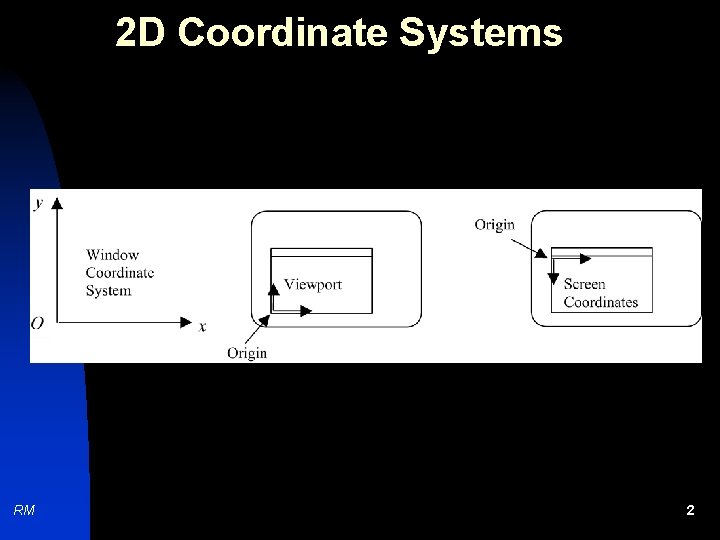
2 D Coordinate Systems RM 2

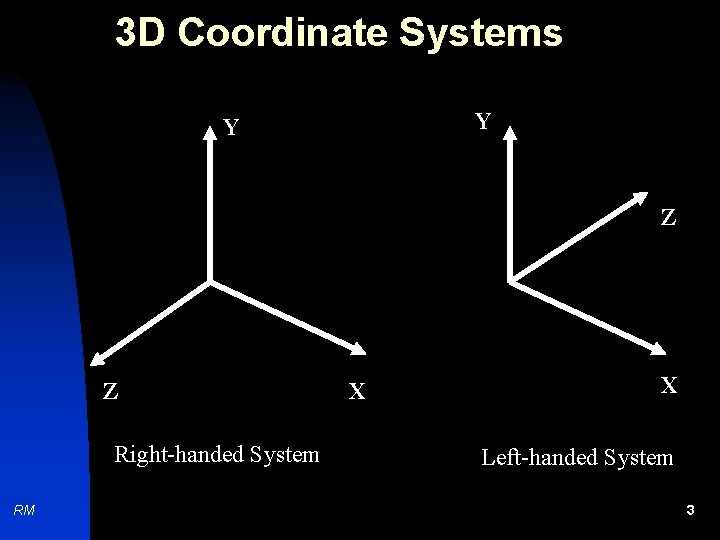
3 D Coordinate Systems Y Y Z Z Right-handed System RM X X Left-handed System 3

3 D Coordinate Systems Right-handed System RM Left-handed System 4

Points and Vectors Y Y v = (x, y) X A point denotes a position in space. RM X A vector is a directed line segment, having both magnitude and direction. 5

Addition and Subtraction of Vectors Two vectors v 1, v 2 can be added to produce the diagonal vector v 1+v 2 according to the parallelogram rule. RM The result of vector subtraction produces v 1 v 2 which is a vector directed from v 2 to v 1. 6

Linear Combination of Vectors • A linear combination of vectors v 1, v 2 is given by v = a v 1+ b v 2, where a, b are constants. • A linear combination of vectors v 1, v 2 always lies in the plane containing the vectors v 1, v 2. Y v 1 v 2 v = a v 1+ b v 2 RM Z X 7

Affine Combination of Vectors • An affine combination of vectors v 1, v 2 is given by v = a v 1+ b v 2, where a, b are constants, and a+b = 1. • In particular, v = (1 t) v 1+ t v 2 is an affine combination of vectors. Y v 1 v = (1 -t)v 1+ t v 2 RM Z X 8

Linear Interpolation of Vectors The affine combination v = (1 t) v 1+ t v 2 performs a linear interpolation between vectors v 1 and v 2 , if 0 t 1. Y v 1 v = (1 -t)v 1+ t v 2 RM Z X 9

Linear Interpolation of Vectors Example: A color (r, g, b) can be treated as a vector. If C 1 = (r 1, g 1, b 1) and C 2 = (r 2, g 2, b 2) are two colors then, a linear interpolation between the two colors is given by C = (1 t) C 1+ t C 2 , 0 t 1. C 1 RM C = (1 t) C 1+ t C 2 10

Unit Vector n RM The magnitude of a vector v is denoted by |v|. n If v=(x, y, z), then |v|= n v/|v| is a unit vector. 11

Vector Dot Product n The dot-product of two vectors v 1 =(x 1, y 1, z 1) and v 2 =(x 2, y 2, z 2) is v 1. v 2 = x 1 x 2 + y 1 y 2 + z 1 z 2. n The cosine of the angle between two vectors v 1, v 2 is computed as follows: cos = (v 1. v 2) / (|v 1| |v 2|). n RM In particular, when the vectors are orthogonal ( = 90 deg), then v 1. v 2 = 0 12

Vector Cross Product n The cross-product of two vectors v 1 =(x 1, y 1, z 1) and v 2 =(x 2, y 2, z 2) is v 1 x v 2 = Also, v 1 x v 2 = RM 13

Vector Cross Product The vector v 1 v 2 is orthogonal to both the vectors v 1, and v 2. The three vectors v 1, v 2, v 1 v 2 form a right-handed system. (Note that v 1 and v 2 are not necessarily orthogonal. Hence the right-handed system is not mutually orthogonal. ) RM 14

Planes n n RM Any three non-collinear points P 1, P 2, P 3 will define a unique plane. Consider the vectors v 1 = P 2 P 1 , and v 2 = P 3 P 1. Both these vectors lie on the plane, and hence the vector n = v 1 v 2 is normal to the plane. 15