Computer Arithmetic Square Root Algorithm By Ali Bohlooli

Computer Arithmetic Square Root Algorithm By: Ali Bohlooli Zefreh s 8026639@ sepahan. iut. ac. ir Professor: Dr. Shadrokh Samavi Computer Arithmetic Date: 1381/ 3/ 4 1 Of 23

Overview Digit by Digit method • Restoring • Non Restoring • SRT –Division –Square Root Computer Arithmetic 2 Of 23

Similarities between Square Root & Division The square-root and division are inverse of multiplication, therefore expect to find some similarities between them. Computer Arithmetic 3 Of 23

Square-Rooting methods 1) Multiplicative methods (Convergence) –Use the reciprocal table –Newton-Raphson, Goldschmidt’s algorithms –Relatively high-speed 2) Subtractive methods (Digit by digit) –Use the subtraction and shift operation –Restoring, Non. Restoring, SRT algorithms –Adopted in most of the recent processors –Area-effective Computer Arithmetic 4 Of 23

Subtractive methods Computer Arithmetic 5 Of 23

Restoring & Non Restoring methods Assume that Qi is partial root in step I and qn-i-1 Is I+1’bit of partial root so Next partial root=r* Qi + qn-i-1 2 And (r Qi + qn-i-1)2=r 2 Qi +2 r Qi qn-i-1 + q 2 n -i-1 Therefore 2 r Qi qn-i-1 + q 2 n -i-1 Must be subtract from partial reminder If radix =2 2 (2 Qi + qn-i-1)2=4 Qi +4 Qi qn-i-1 + q 2 n -i-1 If qn-i-1= ‘ 1’ then it is sufficient to concatenate ‘ 01’ in the right of Qi Computer Arithmetic 6 Of 23
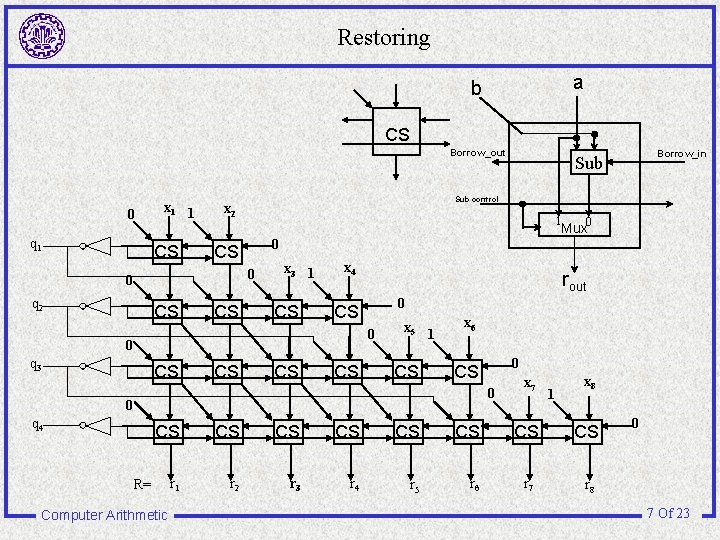
Restoring a b CS Borrow_out 0 q 1 x 1 1 Sub control x 2 1 0 CS 0 0 CS CS x 3 1 CS x 4 rout 0 CS 0 0 q 3 CS CS x 5 CS 1 x 6 0 CS 0 0 q 4 0 Mux CS q 2 Borrow_in Sub CS CS CS r 1 r 2 r 3 r 4 r 5 r 6 R= Computer Arithmetic x 7 1 x 8 CS CS r 7 r 8 0 7 Of 23

Non Restoring Q= X=Q 2 =0. q 1 q 2…qn = 0. x 1 x 2…x 2 n Non Restoring Square root algorithm step 1) R 0= 0. x 1 x 2 ; f 0=0. 01; i=1; step 2)Ri=Ri-1 -fi-1 step 3)if (Ri<0) then (qi ‘ 0’; Ri Ri. x 2 i+1 x 2 i+2; Fi 0. 0. . 0 q 1 q 2…qi 11; Ri+1 Ri+Fi ); Else((qi ‘ 1’; Ri Ri. x 2 i+1 x 2 i+2; Fi 0. 0. . 0 q 1 q 2…qi 01; Ri+1 Ri-Fi ); step 4) i i+1; step 5)if(I<n) then (go to step 3) Else (Q=0. q 1 q 2…qn ) End Computer Arithmetic 8 Of 23

Proof of Non restoring Algorithm (X 11)2=4 x+3 (X 01)2=4 x+1 In restoring algorithm Rj+1 Rj qj+1 2 qj Rj+2 4 Rj-(4 qj+1+1)=4 Rj-8 qj-1 In non restoring algorithm Rj+1 Rj-(4 qj+1) qj+1 2 qj Rj+2 4 Rj+1+(4 qj+1+3)=4 Rj-8 qj-1 Computer Arithmetic 9 Of 23
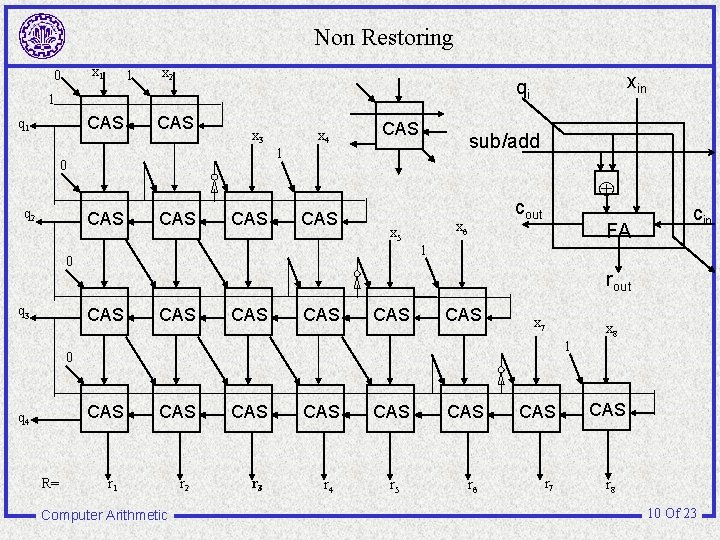
Non Restoring x 1 0 1 x 2 1 CAS q 1 CAS x 3 x 4 CAS CAS CAS Å cout x 6 x 5 FA rout CAS CAS CAS x 7 CAS R= x 8 1 0 q 4 cin 1 0 q 3 sub/add 1 0 q 2 xin qi CAS r 1 Computer Arithmetic r 2 CAS r 3 CAS r 4 CAS r 5 CAS r 6 CAS r 7 CAS r 8 10 Of 23

division & Square-root recursion formulas : the (j+1)th bit of partial root : the jth partial root To find Define , set and evaluate , then (Square-root recursion formula) Rj+1=r. Rj-qj+1 D Computer Arithmetic (division recursion formula) the subtractive square root and division methods are closely related 11 Of 23

Why Assume that X is Radicand its square root is Sm = 0. s 1. . . sm 2 X- Sm = wm 2 -m 에서 2 m m wm = 2 X- 2 Sm 2 wm-1 = 2 m-1 X- 2 m-1 Sm-1 2 2 wm -2 wm-1 = -2 m (Sm -Sm-1) 2 2 = -2 m((sm 2 -m + Sm-1) - Sm-1 ) 2 = -2 m(2 sm Sm-12 -m + sm 2 -2 m ) = -sm(2 Sm-1 + sm 2 -m ) wm = 2 wm-1 - sm(2 Sm-1 + sm 2 -m ) Computer Arithmetic 12 Of 23
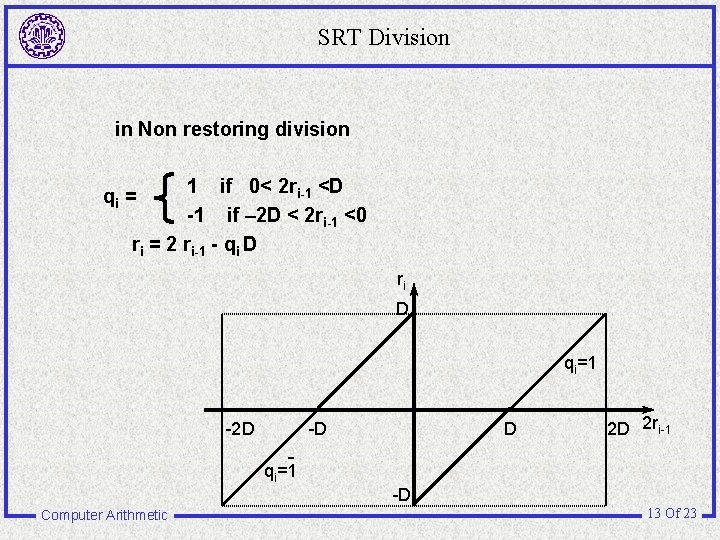
SRT Division in Non restoring division 1 if 0< 2 ri-1 <D -1 if – 2 D < 2 ri-1 <0 ri = 2 ri-1 - qi D qi = ri D qi=1 -2 D -D D 2 D 2 ri-1 qi=1 -D Computer Arithmetic 13 Of 23

SRT Division • • • For qi=0 implies no addition/subtraction However, comparing 2 ri-1 with D or -D takes time if D is a normalized fraction (1/2 £ D < 1), then we can set qi=0 for -1/2 £ 2 ri-1 < 1/2 1 if 2 ri-1 ³ 1/2 qi = 0 if -1/2 £ 2 ri-1 < 1/2 1 if 2 ri-1 < -1/2 ri = 2 ri-1 - qi D (SRT division) Þ 1. |ri| £ D Þ convergence guaranteed 2. comparing 2 ri-1 with 1/2 or -1/2 is easier if 2 ri-1 = 0. 1 xxx Þ 2 ri-1 ³ 1/2 if 2 ri-1 = 1. 0 xxx Þ 2 ri-1 < -1/2 if |X|=|r 0| ³ 1/2 Þ |2 r 0| ³ 1 Þ examine three bits of 2 ri-1 Computer Arithmetic 14 Of 23
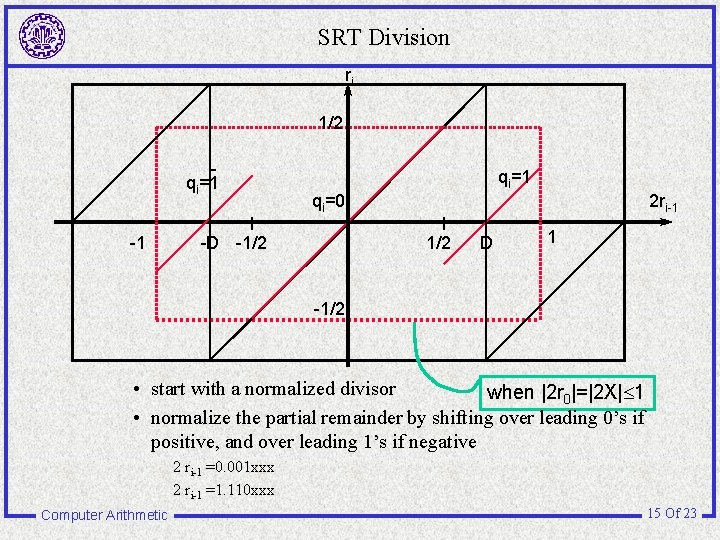
SRT Division ri 1/2 qi=1 -1 qi=0 -D -1/2 2 ri-1 1/2 D 1 -1/2 • start with a normalized divisor when |2 r 0|=|2 X| 1 • normalize the partial remainder by shifting over leading 0’s if positive, and over leading 1’s if negative 2 ri-1 =0. 001 xxx 2 ri-1 =1. 110 xxx Computer Arithmetic 15 Of 23
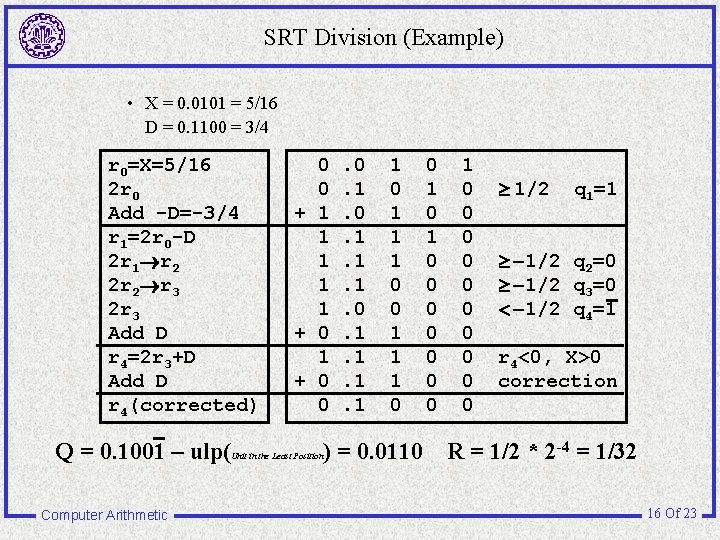
SRT Division (Example) • X = 0. 0101 = 5/16 D = 0. 1100 = 3/4 r 0=X=5/16 2 r 0 Add -D=-3/4 r 1=2 r 0 -D 2 r 1®r 2 2 r 2®r 3 2 r 3 Add D r 4=2 r 3+D Add D r 4(corrected) Q = 0. 1001 – ulp( Computer Arithmetic 0 0 + 1 1 1 + 0 0 Unit in the Least Position . 0. 1. 1. 1. 0. 1. 1 1 0 1 1 1 0 ) = 0. 0110 0 1 0 0 0 0 0 ³ 1/2 q 1=1 ³ -1/2 q 2=0 ³ -1/2 q 3=0 < -1/2 q 4=1 r 4<0, X>0 correction R = 1/2 * 2 -4 = 1/32 16 Of 23

SRT Division How to reduce the number of add/subtract operations from simulation and statistical analysis 1. Average ‘shift’ in the SRT method : 2. 67 average operations : n/2. 67 2. Actual number of operations depends on D The smallest number is achieved when D [17/28, 3/4] with average shift of 3. Approximately D [3/5, 3/4] Computer Arithmetic 17 Of 23

SRT Division To reduce the number of operations, modify the SRT method when D [3/5, 3/4] 1. Examine the possibility of using a multiple of D: in some of the steps during the division use 2 D (one position earlier) if D is too small, or D/2 (one position later) if D is too large. Computer Arithmetic 18 Of 23

Modifying the SRT method 2. Change the comparison constant K K= 1/2 if D [3/5, 3/4] K= 3/8 if D [1/2, 9/16] K= 7/16 if D [9/16, 10/16] D= 0. 1000 K= 0. 1001 0. 1010 0. 1100 0. 1111 1 k 1=3/8 k 2=7/16 k 3=1/2 k 2=5/8 k 3=3/4 0. 0110 0. 0111 0. 1000 0. 1010 0. 1100 Computer Arithmetic 19 Of 23

modifying the SRT method 3 - Radix (=2 m) # of ADD/SUB reduced # of steps = n/m r 0=X; ri= ri– 1–qi. D restoring DIV: ( – 1) qi 0 Non restoring DIV: ( – 1) qi –( – 1) High Radix SRT DIV: qi – ( – 1) /2 Computer Arithmetic 20 Of 23

• Compute Allowable Range of k • (1) k|D| |ri| (convergence condition) ri = ri– 1–qi. D= k. D– D k. D (1) k = /( – 1) Computer Arithmetic 21 Of 23

SRT Division Steps (1) Quotient Selection (QS) qj +1 결정 (2) Divisor Multiple Formation (DMF) qj +1 d 계산 (3) Partial Remainder Formation (PRF) pj +1 = rpj - qj + 1 d (4) Quotient Accumulation (QA) Computer Arithmetic 22 Of 23
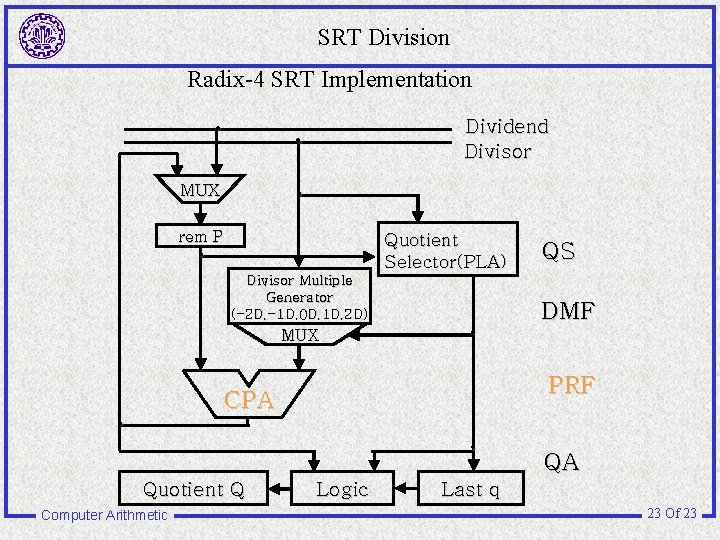
SRT Division Radix-4 SRT Implementation . . Dividend Divisor . MUX . rem P Quotient Selector(PLA) Divisor Multiple Generator (-2 D, -1 D, 0 D, 1 D, 2 D) MUX . . Quotient Q Computer Arithmetic DMF PRF CPA . QS Logic QA Last q 23 Of 23

Refrences • • • 1) “AREA AND PERFORMANCE TRADEOFFS IN FLOATING-POINT DIVIDE AND SQUARE ROOT IMPLEMENTATIONS” , Miriam Leeserl, Dept. of Electrical and Computer Engineering, Northeastern University. Boston, Massachusetts 02115 2) “New algorithm and vlsi architecture for SRT Divesion and square root” S. E. Mc. Quillan, J. V. Mc. Canny, University of Belfast 4)”Computer arithmetic”, kai Hwang 5)http: //citeseer. nj. nec. com/cache/papers/cs/25930/http: z. Szwww 3. hmc. eduz. Sz~harrisz. Szresearch z. Szsrtlong. pdf/srt-division-architectures-models. pdf 6)http: //citeseer. nj. nec. com/cache/papers/cs/3067/ftp: z. Szumunhum. stanford. eduz. Sztrz. Szsrtcircuit s. pdf/harris 97 srt. pdf 7)http: //citeseer. nj. nec. com/cache/papers/cs/4049/http: z. Szwww. ee. umn. eduz. Szgroupsz. Szddpz. Szdi g_serz. Sz. Publicationsz. Szkuhlmannz. Szsqrt. pdf/fast-low-power-shared. pdf 8)http: //citeseer. nj. nec. com/cache/papers/cs/11722/http: z. Szwww. imada. sdu. dkz. Sz~kornerupz. Szpa persz. SRT-thesis. pdf/alternative-implementations-of-srt. pdf 9)http: //citeseer. nj. nec. com/cache/papers/cs/16280/ftp: z. Sztheory. lcs. mit. eduz. Szpubz. Szpeoplez. Sze delmanz. Szpentium. pdf/the-mathematics-of-the. pdf Computer Arithmetic 24 Of 23

References • • 10)http: //citeseer. nj. nec. com/cache/papers/cs/3067/ftp: z. Szumunhum. stanford. eduz. Sztrz. Szdivalgo _TOC. pdf/oberman 97 division. pdf 11)http: //citeseer. nj. nec. com/cache/papers/cs/3944/ftp: z. Szverdon. imag. frz. Szpubz. Sz. ISDz. Szpostscr iptz. Szedtc 96. pdf/asynchronous-srt-dividers-the. pdf 12)http: //citeseer. nj. nec. com/cache/papers/cs/5185/http: z. Szweb. mit. eduz. Sz 18. 337 z. Sz. WWWz. Sz. . z. S z 1995 z. Szlect 3. pdf/about-these-notes-on. pdf 13)http: //citeseer. nj. nec. com/cache/papers/cs/14904/ftp: z. Szftp. mpisb. mpg. dez. Szpubz. Szpapersz. Szreportsz. Sz. MPI-I-96 -1 -001. pdf/burnikel 96 leda. pdf 14)http: //citeseer. nj. nec. com/cache/papers/cs/23982/http: z. Szwww. hpl. hp. comz. Szpersonalz. Sz. Alan _Karpz. Szpublicationsz. Szsqrtdiv. pdf/alan 97 high. pdf 15) vlsi. yonsei. ac. kr/seminar/ Hi-Speed%20 Division%20 Circuit. ppt 16) piglet. uccs. edu/~cs 520/S 99 cha. ppt 17) sdgroup. snu. ac. kr/class/digital. 2000/note/302 L 22. ppt Computer Arithmetic 25 Of 23
- Slides: 25