Computer Arithmetic Computer Arithmetic l Objective In this

Computer Arithmetic

Computer Arithmetic l Objective : In this chapter we will learn why computers use binary numbers instead of decimal numbers and how the basic arithmetic operations are performed the computer using binary numbers. 5/25/2021 2

Why Binary ? M The reasons as follows : M The first and the foremost reason is that electronic and electrical components, by their very nature, operate in a binary mode. MInformation is handled in the computer by electrical/ electronic components such as transistors, semiconductors, wires, etc. all of which can only indicate two states or conditions- on (1) or off (0). MTransistors are either conducting (1) or non-conducting (0); magnetic materials are either magnetized (1) nonmagnetized (0) in one direction; a pulse or voltage is present (1) or not present (0) in wire. 5/25/2021 3

Why Binary MAll information is represented within the computer by the presence or absence of these various signals. M The binary number system, which has only two digit (o and 1), is most suitable and is conveniently used to express the two possible states. M The second reason is that computer circuits only have to handle two binary digits rather than ten decimal digits. The result is that the internal circuit design of computers is simplified to a great extent. This ultimately results in less expensive and more reliable circuits for computers. 5/25/2021 4

Why Binary M Finally, the binary number system is used because everything that can be done with a base of 10 can also be done in binary. How this is achieved has been discussed below. digital 5/25/2021 analog 5

Binary Arithmetic Now we will see how the four basic arithmetic operations are performed inside a computer using binary numbers. Actually, binary arithmetic is much simpler to learn because binary system deals with only two digits - 0 and 1. So all binary numbers are made up of only 0’s and 1’s and when arithmetic operations are performed on these numbers, the results are also in 0’s and 1’s only. 5/25/2021 6

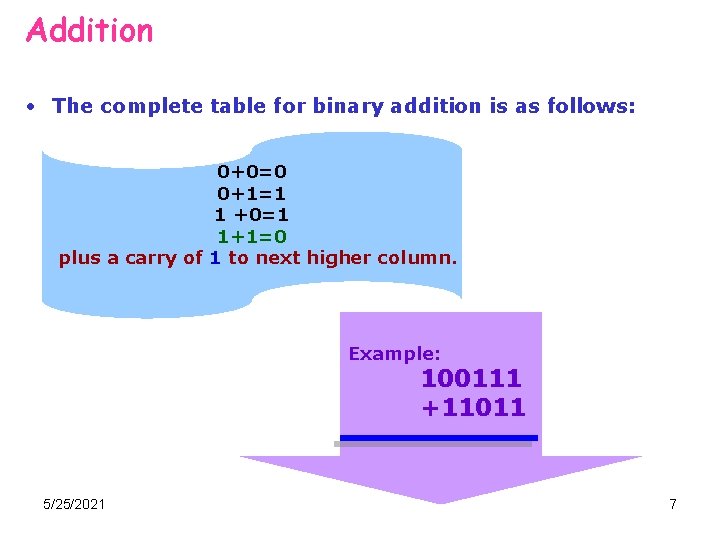
Addition • The complete table for binary addition is as follows: 0+0=0 0+1=1 1 +0=1 1+1=0 plus a carry of 1 to next higher column. Example: 100111 +11011 5/25/2021 7

Subtraction The complete table for binary subtraction is as follows: 0 -0=0 1 -0=1 1 -1=0 0 -1=1 with a borrow from the next column Example: 5/25/2021 1011100 - 0111000 8

Complementary subtraction • For a number which has n digits in it, a complement is defined a the difference between the number and the base raised to the nth power minus one. The definition is illustrated with the following examples: Example : 1. Find the complement of 3710 2. Find the complement of 101012 5/25/2021 9

Complementary subtraction • Subtraction by the complementary method involves the following three steps Ø Find the complement of the number you are subtracting Ø Add this to the number from which you are taking away Ø If there is a carry of 1. Add it is to obtain the result; if there is no carry, recomplement the sum and attach a negative sign to obtain the result 5/25/2021 10

Example : Subtract 5610 from 9210 using complementary method. Solution : step 1: complement of 5610 = (102 -1) - 56 = 99 - 56 =4310 step 2 : Step 3 : Result 5/25/2021 92 +43 (complement of 56) 135 1 (add the carry of 1) = 36 11

Complementary subtraction Examples : 1: Subtract 3510 from 1810 using complementary method. 2. Subtract 01110002 from 10111002 using complementary method. 3. Subtract 1000112 from 010002 using complementary method. 4. Subtract 011102 from 101012 using complementary method. 5/25/2021 12

Multiplication • The complete table for binary multiplication is as follows : 0 0 1 1 x x 0 1 = = 0 0 0 1 • Example : Multiple the binary numbers 1010 and 1001. 5/25/2021 13

Division • The complete table for binary division is as follows : 0/1=0 1/1=1 • Example : Divide 1000012 by 1102 5/25/2021 14