Computer Architecture Chapter 2 a With thanks to

Computer Architecture Chapter 2 a With thanks to M. J. Irwin, D. Patterson, and J. Hennessy for some lecture slide contents

The collection of instructions of a computer Different But with many aspects in common Early computers have different instruction sets computers had very simple instruction sets Simplified implementation Many sets modern computers also have simple instruction § 2. 1 Introduction Instruction Set

The MIPS Instruction Set Used as the example throughout the book Stanford MIPS commercialized by MIPS Technologies See www. mips. com Large share of embedded core market Applications in consumer electronics, network/storage equipment, cameras, printers, … Uses the Reduced Instruction Set Architecture (RISC) approach Typical of many modern ISAs See MIPS Reference Data tear-out card, and Appendixes B and E

MIPS-32 ISA Registers Instruction Categories Computational Load/Store Jump and Branch Floating Point - R 0 - R 31 coprocessor Memory Management PC HI Special LO 3 Instruction Formats: all 32 bits wide op rs rt op rd sa immediate jump target funct R format I format J format

MIPS (& RISC) Design Principles Simplicity favors regularity fixed size instructions small number of instruction formats opcode always the first 6 bits Smaller is faster limited instruction set limited number of registers in register file limited number of addressing modes Make the common case fast arithmetic operands from the register file (load-store machine) allow instructions to contain immediate operands Good design demands good compromises three instruction formats

Add and subtract, three operands Two sources and one destination add a, b, c All # a gets b + c arithmetic operations have this form Design Principle 1: Simplicity favors regularity Regularity makes implementation simpler Simplicity enables higher performance at lower cost § 2. 2 Operations of the Computer Hardware Arithmetic Operations

Arithmetic Example C code: f = (g + h) - (i + j); Compiled “MIPS code”: add t 0, g, h add t 1, i, j sub f, t 0, t 1 # temp t 0 = g + h # temp t 1 = i + j # f = t 0 - t 1

MIPS Arithmetic Instructions MIPS assembly language arithmetic statement add $t 0, $s 1, $s 2 sub $t 0, $s 1, $s 2 Each arithmetic instruction performs one operation Each specifies exactly three operands that are all contained in the datapath’s register file ($t 0, $s 1, $s 2) destination source 1 Instruction 0 op source 2 Format (R format) 17 18 8 0 0 x 22

MIPS Instruction Fields MIPS fields are given names to make them easier to refer to op op rs 6 -bits rt rd shamt funct opcode that specifies the operation rs 5 -bits register file address of the first source operand rt 5 -bits register file address of the second source operand rd 5 -bits register file address of the result’s destination shamt 5 -bits shift amount (for shift instructions) function code augmenting the opcode 6 -bits

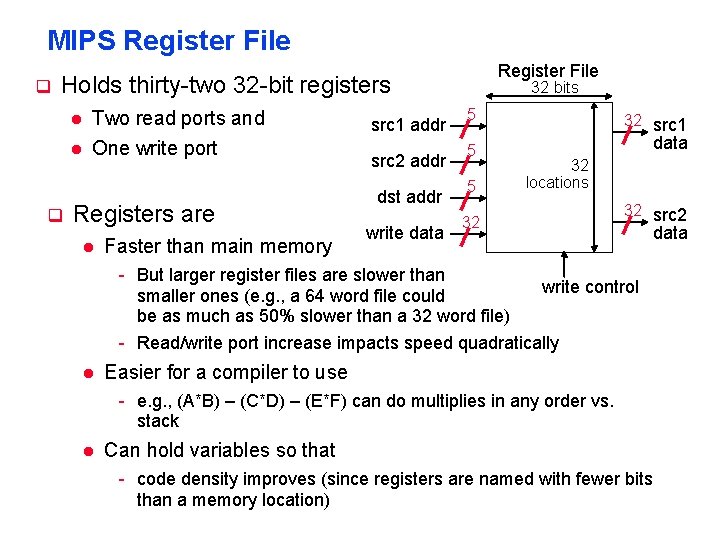
Arithmetic instructions use register operands MIPS has a 32 × 32 -bit register file Use for frequently accessed data Numbered 0 to 31 32 -bit data called a “word” Assembler names $t 0, $t 1, …, $t 9 for temporary values $s 0, $s 1, …, $s 7 for saved variables Design Principle 2: Smaller is faster Compare with main memory: millions of locations § 2. 3 Operands of the Computer Hardware Register Operands

MIPS Register File Holds thirty-two 32 -bit registers Two read ports and One write port Registers are Faster than main memory src 1 addr src 2 addr dst addr write data 32 bits 5 5 5 32 src 1 data 32 locations 32 32 src 2 - But larger register files are slower than write control smaller ones (e. g. , a 64 word file could be as much as 50% slower than a 32 word file) - Read/write port increase impacts speed quadratically Easier for a compiler to use - e. g. , (A*B) – (C*D) – (E*F) can do multiplies in any order vs. stack Can hold variables so that - code density improves (since registers are named with fewer bits than a memory location) data

Register Operand Example C code: f = (g + h) - (i + j); Compiler puts f, g, h, i, j in $s 0, …, $s 4 Compiled MIPS code: add $t 0, $s 1, $s 2 add $t 1, $s 3, $s 4 sub $s 0, $t 1

Registers vs. Memory Registers are faster to access than memory Operating on memory data requires loads and stores More instructions to be executed Compiler possible must use registers for variables as much as Only spill to memory for less frequently used variables Register optimization is important!

Immediate Operands Constant data specified in an instruction addi $s 3, 4 No subtract immediate instruction Just use a negative constant addi $s 2, $s 1, -1 Design Principle 3: Make the common case fast Small constants are common (50% of MIPS arithmetic instructions in SPEC 2006 use constants!) Immediate operand avoids a load instruction

The Constant Zero MIPS register 0 ($zero) is the constant 0 Cannot be overwritten Useful for common operations E. g. , move between registers add $t 2, $s 1, $zero

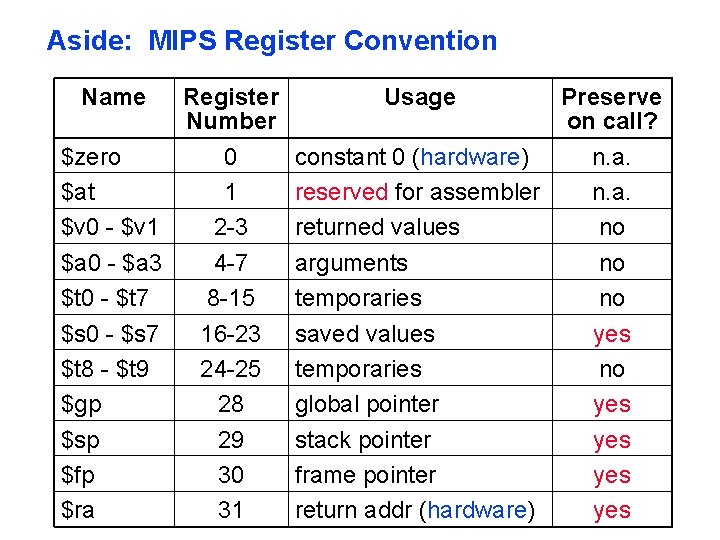
Aside: MIPS Register Convention Name Register Number $zero 0 $at 1 $v 0 - $v 1 2 -3 $a 0 - $a 3 4 -7 $t 0 - $t 7 8 -15 $s 0 - $s 7 16 -23 $t 8 - $t 9 24 -25 $gp 28 $sp 29 $fp 30 $ra 31 Usage Preserve on call? constant 0 (hardware) n. a. reserved for assembler n. a. returned values no arguments no temporaries no saved values yes temporaries no global pointer yes stack pointer yes frame pointer yes return addr (hardware) yes

MIPS Memory Access Instructions MIPS has two basic data transfer instructions for accessing memory lw sw $t 0, 4($s 3) $t 0, 8($s 3) #load word from memory #store word to memory The data is loaded into (lw) or stored from (sw) a register in the register file – a 5 bit address The memory address – a 32 bit address – is formed by adding the contents of the base address register to the offset value A 16 -bit field meaning access is limited to memory locations within a region of 213 or 8, 192 words ( 215 or 32, 768 bytes) of the address in the base register

Memory Operand Example 1 C code: g = h + A[8]; g in $s 1, h in $s 2, base address of A in $s 3 Compiled MIPS code: Index 8 requires offset of 32 bytes - 4 bytes per word lw $t 0, 32($s 3) add $s 1, $s 2, $t 0 offset # load word base register

Memory Operand Example 2 C code: A[12] = h + A[8]; h in $s 2, base address of A in $s 3 Compiled MIPS code: Index 8 requires offset of 32 bytes Index 12 requires offset of 48 bytes lw $t 0, 32($s 3) add $t 0, $s 2, $t 0 sw $t 0, 48($s 3) # load word # store word

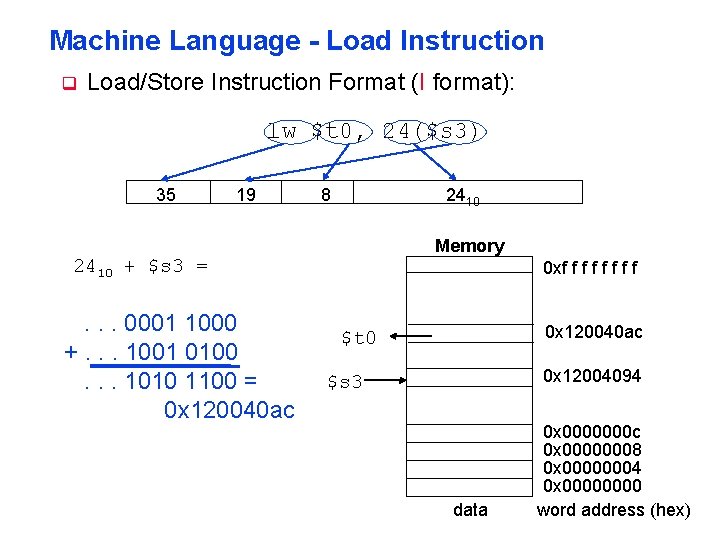
Machine Language - Load Instruction Load/Store Instruction Format (I format): lw $t 0, 24($s 3) 35 19 8 24 10 Memory 2410 + $s 3 = . . . 0001 1000 +. . . 1001 0100. . . 1010 1100 = 0 x 120040 ac 0 xf f f f 0 x 120040 ac $t 0 0 x 12004094 $s 3 data 0 x 0000000 c 0 x 00000008 0 x 00000004 0 x 0000 word address (hex)

Byte Addresses Since 8 -bit bytes are so useful, most architectures address individual bytes in memory Alignment restriction - the memory address of a word must be on natural word boundaries (a multiple of 4 in MIPS-32) Big Endian: leftmost byte is word address IBM 360/370, Motorola 68 k, MIPS, Sparc, HP PA Little Endian: rightmost byte is word address Intel IA-32, DEC Vax, DEC Alpha (Windows NT) 3 2 1 little endian byte 0 0 msb 0 big endian byte 0 lsb 1 2 3

Aside: Loading and Storing Bytes MIPS provides special instructions to move bytes lb $t 0, 1($s 3) #load byte from memory sb $t 0, 6($s 3) #store byte to 0 x 28 What 19 8 memory 16 bit offset 8 bits get loaded and stored? load byte places the byte from memory in the rightmost 8 bits of the destination register - what happens to the other bits in the register? store byte takes the byte from the rightmost 8 bits of a register and writes it to a byte in memory - what happens to the other bits in the memory word?

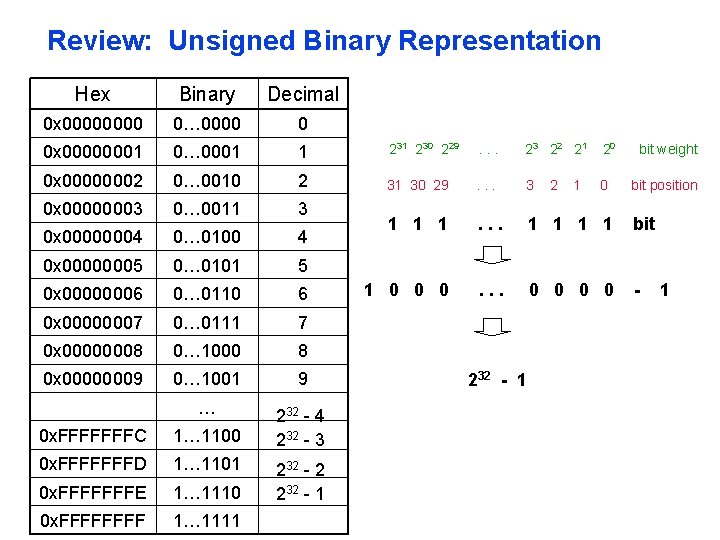
Given an n-bit number Range: 0 to +2 n – 1 Example 0000 0000 10112 = 0 + … + 1× 23 + 0× 22 +1× 21 +1× 20 = 0 + … + 8 + 0 + 2 + 1 = 1110 Using 32 bits 0 to +4, 294, 967, 295 § 2. 4 Signed and Unsigned Numbers Unsigned Binary Integers

2 s-Complement Signed Integers Given an n-bit number Range: – 2 n – 1 to +2 n – 1 Example 1111 1111 11002 = – 1× 231 + 1× 230 + … + 1× 22 +0× 21 +0× 20 = – 2, 147, 483, 648 + 2, 147, 483, 644 = – 410 Using 32 bits – 2, 147, 483, 648 to +2, 147, 483, 647

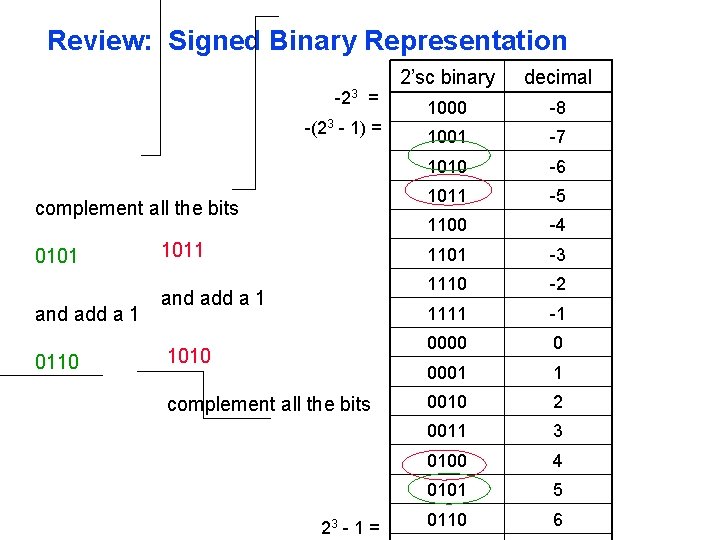
Review: Unsigned Binary Representation Hex Binary Decimal 0 x 0000 0… 0000 0 0 x 00000001 0… 0001 1 230 229 . . . 2 3 22 21 20 0 x 00000002 0… 0010 2 31 30 29 . . . 3 0 0 x 00000003 0… 0011 3 0 x 00000004 0… 0100 4 1 1 1 . . . 1 1 bit 0 x 00000005 0… 0101 5 0 x 00000006 0… 0110 6 1 0 0 0 . . . 0 0 - 0 x 00000007 0… 0111 7 0 x 00000008 0… 1000 8 0 x 00000009 0… 1001 9 … 232 - 4 232 - 3 0 x. FFFFFFFC 1… 1100 0 x. FFFFFFFD 1… 1101 0 x. FFFFFFFE 1… 1110 0 x. FFFF 1… 1111 232 - 2 232 - 1 2 1 bit weight bit position 1

Review: Signed Binary Representation -23 = -(23 - 1) = complement all the bits 0101 and add a 1 0110 1011 and add a 1 1010 complement all the bits 23 - 1 = 2’sc binary decimal 1000 -8 1001 -7 1010 -6 1011 -5 1100 -4 1101 -3 1110 -2 1111 -1 0000 0 0001 1 0010 2 0011 3 0100 4 0101 5 0110 6

2 s-Complement Signed Integers Bit 31 is sign bit 1 for negative numbers 0 for non-negative numbers –(– 2 n – 1) can’t be represented Non-negative numbers have the same unsigned and 2 scomplement representation Some specific numbers 0: 0000 … 0000 – 1: 1111 … 1111 Most-negative: 1000 0000 … 0000 Most-positive: 0111 1111 … 1111

Signed Negation Complement and add 1 Complement means 1 → 0, 0 → 1 Example: negate +2 +2 = 0000 … 00102 – 2 = 1111 … 11012 + 1 = 1111 … 11102

Sign Extension Representing In a number using more bits Preserve the numeric value MIPS instruction set addi: extend immediate value lb, lh: extend loaded byte/halfword beq, bne: extend the displacement Replicate the sign bit to the left c. f. unsigned values: extend with 0 s Examples: 8 -bit to 16 -bit +2: 0000 0010 => 0000 0010 – 2: 1111 1110 => 1111 1110

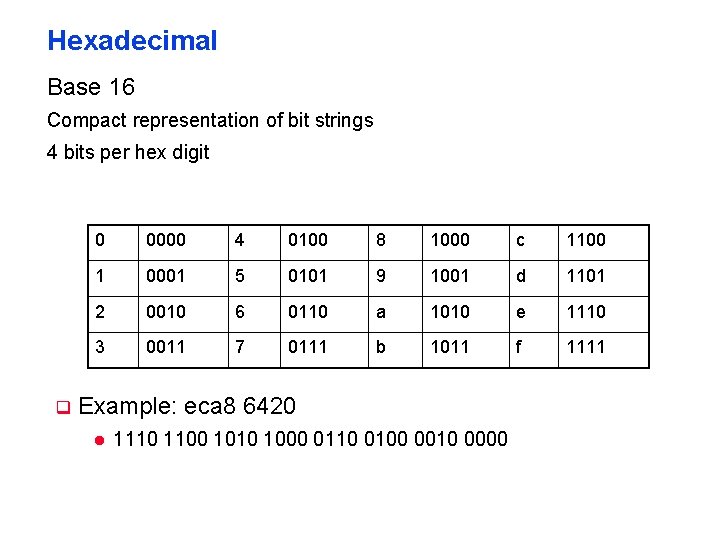
Hexadecimal Base 16 Compact representation of bit strings 4 bits per hex digit 0 0000 4 0100 8 1000 c 1100 1 0001 5 0101 9 1001 d 1101 2 0010 6 0110 a 1010 e 1110 3 0011 7 0111 b 1011 f 1111 Example: eca 8 6420 1110 1100 1010 1000 0110 0100 0010 0000

Small constants are used often in typical code Possible approaches? put “typical constants” in memory and load them create hard-wired registers (like $zero) for constants like 1 have special instructions that contain constants ! addi $sp, 4 #$sp = $sp + 4 slti $t 0, $s 2, 15 #$t 0 = 1 if $s 2<15 Machine format (I format): 0 x 0 A 18 8 0 x 0 F The constant is kept inside the instruction itself! Immediate format limits values to the range +215– 1 to -215 § 2. 5 Representing Instructions in the Computer MIPS Immediate Instructions

Aside: How About Larger Constants? We'd also like to be able to load a 32 bit constant into a register, for this we must use two instructions a new "load upper immediate" instruction lui $t 0, 10101010 16 0 8 10101010 2 Then must get the lower order bits right, use ori $t 0, 1010101010101010 0000000000000000 1010101010101010

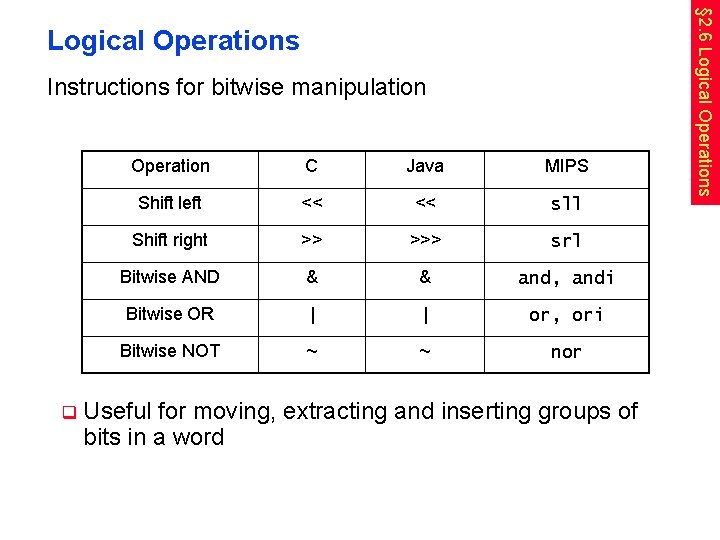
Instructions for bitwise manipulation Operation C Java MIPS Shift left << << sll Shift right >> >>> srl Bitwise AND & & and, andi Bitwise OR | | or, ori Bitwise NOT ~ ~ nor Useful for moving, extracting and inserting groups of bits in a word § 2. 6 Logical Operations

MIPS Shift Operations Need operations to pack and unpack 8 -bit characters into 32 -bit words Shifts move all the bits in a word left or right sll $t 2, $s 0, 8 #$t 2 = $s 0 << 8 bits srl $t 2, $s 0, 8 #$t 2 = $s 0 >> 8 bits Instruction 0 Such Format (R format) 16 10 8 0 x 00 shifts are called logical because they fill with zeros Notice that a 5 -bit shamt field is enough to shift a 32 -bit value 25 – 1 or 31 bit positions

MIPS Logical Operations There a number of bit-wise logical operations in the MIPS ISA and $t 0, $t 1, $t 2 #$t 0 = $t 1 & $t 2 or $t 0, $t 1, $t 2 #$t 0 = $t 1 | $t 2 nor $t 0, $t 1, $t 2 #$t 0 = not($t 1 | $t 2) Instruction Format (R format) 0 9 10 8 0 0 x 24 andi $t 0, $t 1, 0 x. FF 00 #$t 0 = $t 1 & ff 00 ori $t 0, $t 1, 0 x. FF 00 #$t 0 = $t 1 | ff 00 Instruction Format (I format) 0 x 0 D 9 8 0 x. FF 00

Shift Operations shamt: Shift op rs rt rd shamt funct 6 bits 5 bits 6 bits # positions to shift left logical Shift left and fill with bits with 0 sll by i bits multiplies by 2 i Shift right logical Shift right and fill with bits with 0 srl by i bits divides by 2 i (unsigned only)

OR Operations Useful to include bits in a word Set some bits to 1, leave others unchanged or $t 0, $t 1, $t 2 # $t 1 is the “OR mask” $t 2 0000 0000 1101 1100 0000 $t 1 0000 0011 1100 0000 $t 0 0000 0011 1100 0000

AND Operations Useful to mask bits in a word Clear some bits to 0, leave others unchanged and $t 0, $t 1, $t 2 # $t 1 is the “AND mask” $t 2 0000 0000 1101 1100 0000 $t 1 0000 0011 1100 0000 $t 0 0000 0000 1100 0000

NOT Operations Useful Change 0 to 1, and 1 to 0 MIPS to invert bits in a word has NOR 3 -operand instruction a NOR b == NOT ( a OR b ) nor $t 0, $t 1, $zero Register 0: always read as zero $t 1 0000 0011 1100 0000 $t 0 1111 1100 0011 1111