Computer Architecture and Number Systems Topics What is

Computer Architecture and Number Systems Topics • What is Computer? • Major Computer Components • Computer Components Interconnection • Data Representation o o o Bits, Bytes, and Words The Decimal Number System The Binary Number System Converting from Binary to Decimal, Decimal to Binary The Hexadecimal Number System Converting from Hexadecimal to Decimal, Decimal to Hexadecimal CMSC 104, Section 301, Fall 2002 1 Lecture 02, 9/04/02

What is Computer? • A data processing machine capable of performing computations and making logical decisions very fast. • Consists of hardware such as keyboard, screen, mouse, disks, memory, CD-ROM, and processing units. • A program (software) is a set of instructions written in a computer language that runs on a computer. CMSC 104, Section 301, Fall 2002 2 Lecture 02, 9/04/02

Major Computer Components • Memory Unit (Main Memory, Secondary Storage Unit) • Arithmetic and Logic Unit (ALU), Central Processing Unit (CPU) • Input/Output (I/O) Unit CMSC 104, Section 301, Fall 2002 3 Lecture 02, 9/04/02

Memory Unit • Memory unit stores information such as computer programs, data, or documents. • Two types of memory devices: 1. Primary Storage or Main Memory 2. Secondary Storage CMSC 104, Section 301, Fall 2002 4 Lecture 02, 9/04/02

Memory Unit (con’t) • • Main memory is fast and expensive. • Stores frequently accessed information such as programs and data during their execution. • Is volatile storage. That is, if power is lost, the information in main memory is lost. Secondary storage is slower and cheaper. • Disks (floppy, hard, removable), Tapes, CDs, DVDs. • Is non-volatile, that is persistent (permanent) storage. CMSC 104, Section 301, Fall 2002 5 Lecture 02, 9/04/02

Memory Unit (con’t) • • Main memory consists of a collections of storage locations. Data are read from or written to memory in cells. A cell can be 8 – 64 bits. Address is used to uniquely identify a cell location. Cells may be grouped into words. E. g. , four 8 -bit cells forms one word. CMSC 104, Section 301, Fall 2002 6 Lecture 02, 9/04/02

Memory Unit (con’t) • Memory Access Methods • Sequential access memory • Read memory address one after another, e. g. tape. • Random-access memory (RAM) • Any location can be read by specifying its address, e. g. main memory, disks, CDs, DVDs. CMSC 104, Section 301, Fall 2002 7 Lecture 02, 9/04/02

Input/Output (I/O) Unit • Input/Output Unit Input unit accepts input data and programs from an input device. o Output unit sends the results of processing (output) to an output device. • More generally, these devices are known as peripheral devices. o Input device - keyboard, mouse, scanner o Output device - monitor, printer o I/O device - disk drive (floppy, hard, removable), CD or DVD drive o CMSC 104, Section 301, Fall 2002 8 Lecture 02, 9/04/02

ALU, CPU ALU performs calculations (such as addition, subtraction, multiplication, division) and logical operations (e. g. comparing two numbers). • CPU is the “brain” of the computer. • Controls operations of other components, memory, ALU, I/O. • Tells input unit when info is ready to be read into the memory unit. • Tells output unit when to send info from the memory unit to an output device. • CMSC 104, Section 301, Fall 2002 9 Lecture 02, 9/04/02

Computer Components Interconnection • CPU and memory are connected by a bus. • Connecting I/O devices o o I/O devices are slower than CPU/memory. Can’t connect directly to Bus. Need an I/O controller or interface to handle the differences in speed between the I/O device and the bus. • A bus is a group of parallel wires that carry control signals and data between CPU and memory. CMSC 104, Section 301, Fall 2002 10 Lecture 02, 9/04/02

Computer Components Interconnection • Three types of Bus o o o Data Bus Address Bus Control Bus • Data bus consists of many wires. Each wire carries 1 bit at a time. The # of wires (bits) needed = size of a word. If the word is 32 bits in a computer, then we need 32 -bit data bus. CMSC 104, Section 301, Fall 2002 11 Lecture 02, 9/04/02

Computer Components Interconnection • Address bus allows access to a particular word in a memory. The number of wires = log 2(total number of memory words). If the memory has 2 n words, address bus needs to carry n bits at a time. • Control bus carries communication signals between CPU and memory. The number of bits used = log 2(total number of control commands). CMSC 104, Section 301, Fall 2002 12 Lecture 02, 9/04/02

Data Representation Data types: • Text • Number • Image • Audio • Video CMSC 104, Section 301, Fall 2002 13 Lecture 02, 9/04/02

Bits, Bytes, and Words A bit is a single binary digit (a 1 or 0). A byte is 8 bits A word is 32 bits (that is, 4 bytes) Long word = 8 bytes = 64 bits Quad word = 16 bytes = 128 bits Programming languages use these standard number of bits when organizing data storage and access. • What do you call 4 bits? (hint: it is a small byte) • • • CMSC 104, Section 301, Fall 2002 14 Lecture 02, 9/04/02

Number Systems • The data in memory is represented in terms of 1’s and 0’s. • Therefore, thinking about how information is stored in RAM requires knowledge of the binary (base 2) number system. • Let’s review the decimal (base 10) number system first. CMSC 104, Section 301, Fall 2002 15 Lecture 02, 9/04/02

The Decimal Number System • The decimal number system is a positional number system. • Example: 1 2 65 5 X 100 = 5 103 102 101 100 6 X 101 = 60 2 X 102 = 200 1 X 103 = 1000 CMSC 104, Section 301, Fall 2002 16 Lecture 02, 9/04/02

The Decimal Number System (con’t) • The decimal number system is also known as base 10. The values of the positions are calculated by taking 10 raised to some power. • Why is the base 10 for decimal numbers? o Because we use 10 digits, the digits 0 through 9. CMSC 104, Section 301, Fall 2002 17 Lecture 02, 9/04/02

The Binary Number System • The binary number system is also known as base 2. The values of the positions are calculated by taking 2 to some power. • Why is the base 2 for binary numbers? o Because we use 2 digits, the digits 0 and 1. CMSC 104, Section 301, Fall 2002 18 Lecture 02, 9/04/02

The Binary Number System (con’t) • The binary number system is also a positional numbering system. • Instead of using ten digits, 0 - 9, the binary system uses only two digits, 0 and 1. • Example of a binary number and the values of the positions: 1 0 0 1 1 0 1 26 CMSC 104, Section 301, Fall 2002 25 24 23 19 22 21 20 Lecture 02, 9/04/02

Converting from Binary to Decimal 1 0 0 1 2 6 2 5 2 4 23 2 2 21 2 0 20 = 1 21 = 2 22 = 4 23 = 8 CMSC 104, Section 301, Fall 2002 24 = 16 25 = 32 26 = 64 20 1 X 20 = 1 0 X 21 = 0 0 X 22 = 0 1 X 23 = 8 0 X 24 = 0 0 X 25 = 0 1 X 26 = 64 7310 Lecture 02, 9/04/02

Converting from Binary to Decimal (con’t) Practice conversions: Binary 101 101101 CMSC 104, Section 301, Fall 2002 Decimal 21 Lecture 02, 9/04/02

Converting From Decimal to Binary (con’t) • Perform successive divisions by 2, placing the remainder (0 or 1) in each of the positions from right to left. • Continue until the quotient is zero. • Example: 4410 44 / 2 22 / 2 11 / 2 5/2 2/2 1/2 Done = 22 = 11 =5 =2 =1 =0 CMSC 104, Section 301, Fall 2002 rem = 0 rem = 1 answer = 1 0 1 1 0 0 2 22 Lecture 02, 9/04/02

Converting From Decimal to Binary (con’t) Practice conversions: Decimal Binary 59 82 175 CMSC 104, Section 301, Fall 2002 23 Lecture 02, 9/04/02

Working with Large Numbers 1101000010100110 = ? • Humans don’t work well with binary numbers; there are too many digits to deal with. • Memory addresses and other data can be quite large. Therefore, we sometimes use the hexadecimal number system. CMSC 104, Section 301, Fall 2002 24 Lecture 02, 9/04/02

The Hexadecimal Number System • The hexadecimal (hex) number system is also known as base 16. The values of the positions are calculated by taking 16 to some power. • Why is the base 16 for hexadecimal numbers ? o Because we use 16 symbols, the digits 0 and 1 and the letters A through F. CMSC 104, Section 301, Fall 2002 25 Lecture 02, 9/04/02

The Hexadecimal Number System (con’t) • Example of a hexadecimal number and the values of the positions: 3 C 8 B 0 5 1 166 165 164 163 162 161 160 CMSC 104, Section 301, Fall 2002 26 Lecture 02, 9/04/02

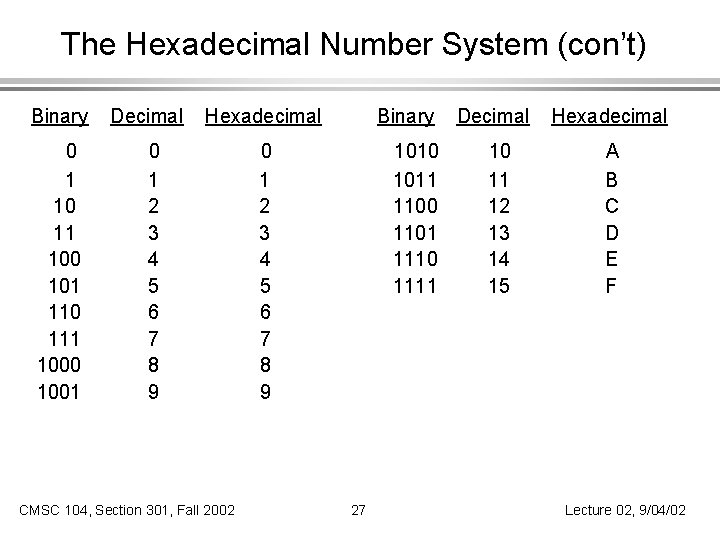
The Hexadecimal Number System (con’t) Binary 0 1 10 11 100 101 110 111 1000 1001 Decimal Hexadecimal 0 1 2 3 4 5 6 7 8 9 CMSC 104, Section 301, Fall 2002 Binary 0 1 2 3 4 5 6 7 8 9 1010 1011 1100 1101 1110 1111 27 Decimal 10 11 12 13 14 15 Hexadecimal A B C D E F Lecture 02, 9/04/02

Converting From Hexadecimal to Decimal • Example: Convert 1 A 5 F 16 to decimal. 1 A 5 F 163 4096 162 161 160 256 16 1 Recall: A 16 = 1010 and F 16 = 1510. = 1 x 4096 + A x 256 + 5 x 16 + F x 1 = 1 x 4096 + 10 x 256 + 5 x 16 + 15 x 1 = 4096 + 2560 + 80 + 15 = 675110 CMSC 104, Section 301, Fall 2002 28 Lecture 02, 9/04/02

Converting From Decimal to Hexadeciaml • • • Perform successive divisions by 16, placing the remainder (0 -9, A-F) in each of the positions from right to left. Continue until the quotient is zero. Example: Convert 14310 to hex. 143 / 16 = 8 8 / 16 = 0 Done rem = 1510 = F 16 rem = 8 answer = 8 F 16 To Check: 8 x 16 + 15 = 128 + 15 = 14310 CMSC 104, Section 301, Fall 2002 29 Lecture 02, 9/04/02

Example of Equivalent Numbers Binary: 1 0 0 0 0 1 1 12 Decimal: 2064710 Hexadecimal: 50 A 716 Notice that the number of digits needed is smaller as the base increases. CMSC 104, Section 301, Fall 2002 30 Lecture 02, 9/04/02

Next Class • Operating System and Using Linux. • Homework #1 due beginning of class on September 9. CMSC 104, Section 301, Fall 2002 31 Lecture 02, 9/04/02