Computer Architecture A Quantitative Approach Fifth Edition Chapter

Computer Architecture A Quantitative Approach, Fifth Edition Chapter 4 Data-Level Parallelism in Vector, SIMD, and GPU Architectures Copyright © 2012, Elsevier Inc. All rights reserved. 1

n SIMD architectures can exploit significant datalevel parallelism for: n n n matrix-oriented scientific computing media-oriented image and sound processors SIMD is more energy efficient than MIMD n n n Introduction Only needs to fetch one instruction per data operation Makes SIMD attractive for personal mobile devices SIMD allows programmer to continue to think sequentially Copyright © 2012, Elsevier Inc. All rights reserved. 2

n Vector architectures SIMD extensions Graphics Processor Units (GPUs) n For x 86 processors: n n n Introduction SIMD Parallelism Expect two additional cores per chip per year SIMD width to double every four years Potential speedup from SIMD to be twice that from MIMD! Copyright © 2012, Elsevier Inc. All rights reserved. 3

n Basic idea: n n Read sets of data elements into “vector registers” Operate on those registers Disperse the results back into memory Vector Architectures Registers are controlled by compiler n n Used to hide memory latency Leverage memory bandwidth Copyright © 2012, Elsevier Inc. All rights reserved. 4

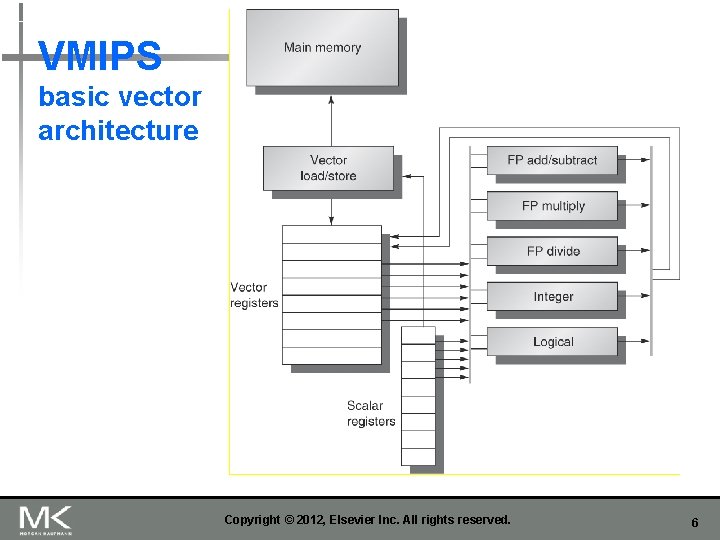
n Example architecture: VMIPS n n Loosely based on Cray-1 Vector registers n n Fully pipelined Data and control hazards are detected Vector load-store unit n n n Each register holds a 64 -element, 64 bits/element vector Register file has 16 read ports and 8 write ports Vector functional units n n Vector Architectures VMIPS Fully pipelined One word per clock cycle after initial latency Scalar registers n n 32 general-purpose registers 32 floating-point registers Copyright © 2012, Elsevier Inc. All rights reserved. 5

VMIPS basic vector architecture Copyright © 2012, Elsevier Inc. All rights reserved. 6

n n n ADDVV. D: add two vectors ADDVS. D: add vector to a scalar LV/SV: vector load and vector store from address Vector Architectures VMIPS Instructions Example: DAXPY (Y=a*X + Y) L. D F 0, a ; load scalar a LV V 1, Rx ; load vector X MULVS. D V 2, V 1, F 0 ; vector-scalar multiply LV V 3, Ry ; load vector Y ADDVV V 4, V 2, V 3 ; add SV Ry, V 4 ; store the result Requires 6 instructions vs. almost 600 for MIPS Copyright © 2012, Elsevier Inc. All rights reserved. 7

n Execution time depends on three factors: n n VMIPS functional units consume one element per clock cycle n n Length of operand vectors Structural hazards Data dependencies Vector Architectures Vector Execution Time Execution time is approximately the vector length Convey n Set of vector instructions that could potentially execute together Copyright © 2012, Elsevier Inc. All rights reserved. 8

n n Sequences with read-after-write dependency hazards can be in the same convey via chaining Chaining n n Vector Architectures Chimes Allows a vector operation to start as soon as the individual elements of its vector source operand become available Chime n n n Unit of time to execute one convey m conveys executes in m chimes For vector length of n, requires m x n clock cycles Copyright © 2012, Elsevier Inc. All rights reserved. 9

LV MULVS. D LV ADDVV. D SV Convoys: 1 LV 2 LV 3 SV V 1, Rx V 2, V 1, F 0 V 3, Ry V 4, V 2, V 3 Ry, V 4 ; load vector X ; vector-scalar multiply ; load vector Y ; add two vectors ; store the sum Vector Architectures Example MULVS. D ADDVV. D 3 chimes, 2 FP ops per result, cycles per FLOP = 1. 5 For 64 element vectors, requires 64 x 3 = 192 clock cycles Copyright © 2012, Elsevier Inc. All rights reserved. 10

n Start up time n n Latency of vector functional units Assume the same as Cray-1: n n n Vector Architectures Challenges Floating-point add => 6 clock cycles Floating-point multiply => 7 clock cycles Floating-point divide => 20 clock cycles Vector load => 12 clock cycles Improvements: n n n n > 1 element per clock cycle Non-64 wide vectors IF statements in vector code Memory system optimizations to support vector processors Multiple dimensional matrices Sparse matrices Programming a vector computer Copyright © 2012, Elsevier Inc. All rights reserved. 11

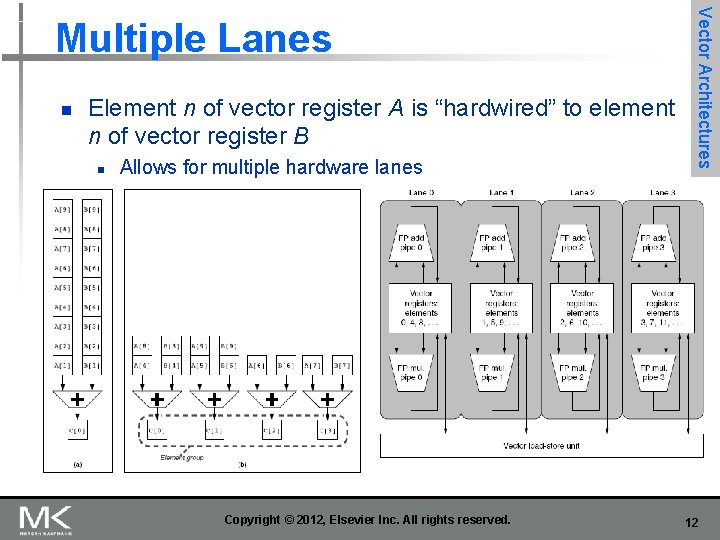
n Element n of vector register A is “hardwired” to element n of vector register B n Allows for multiple hardware lanes Copyright © 2012, Elsevier Inc. All rights reserved. Vector Architectures Multiple Lanes 12

n n n Vector length not known at compile time? Use Vector Length Register (VLR) Use strip mining for vectors over the maximum length: Vector Architectures Vector Length Register low = 0; VL = (n % MVL); /*find odd-size piece using modulo op ; MVL=Max Vector Length% */ for (j = 0; j <= (n/MVL); j=j+1) { /*outer loop*/ for (i = low; i < (low+VL); i=i+1) /*runs for length VL*/ Y[i] = a * X[i] + Y[i] ; /*main operation*/ low = low + VL; /*start of next vector*/ VL = MVL; /*reset the length to maximum vector length*/ } Copyright © 2012, Elsevier Inc. All rights reserved. 13

n n Consider: for (i = 0; i < 64; i=i+1) if (X[i] != 0) X[i] = X[i] – Y[i]; Use vector mask register to “disable” elements: LV LV L. D SNEVS. D SUBVV. D SV n V 1, Rx V 2, Ry F 0, #0 V 1, F 0 V 1, V 2 Rx, V 1 Vector Architectures Vector Mask Registers ; load vector X into V 1 ; load vector Y ; load FP zero into F 0 ; sets VM(i) to 1 if V 1(i)!=F 0 ; subtract under vector mask ; store the result in X GFLOPS rate decreases! Copyright © 2012, Elsevier Inc. All rights reserved. 14

n n Memory system must be designed to support high bandwidth for vector loads and stores Spread accesses across multiple banks n n Vector Architectures Memory Banks Control bank addresses independently Load or store non sequential words Support multiple vector processors sharing the same memory Example: n n n 32 processors, each generating 4 loads and 2 stores/cycle Processor cycle time is 2. 167 ns, SRAM cycle time is 15 ns How many memory banks needed? Copyright © 2012, Elsevier Inc. All rights reserved. 15

n n Consider: for (i = 0; i < 100; i=i+1) for (j = 0; j < 100; j=j+1) { A[i][j] = 0. 0; for (k = 0; k < 100; k=k+1) A[i][j] = A[i][j] + B[i][k] * D[k][j]; } Vector Architectures Stride Must vectorize multiplication of rows of B with columns of D Use non-unit stride Bank conflict (stall) occurs when the same bank is hit faster than bank busy time: n n #banks / LCM(stride, #banks) < bank busy time See example pg 279 Copyright © 2012, Elsevier Inc. All rights reserved. 16

Vector Architectures Scatter-Gather n n Consider: for (i = 0; i < n; i=i+1) A[K[i]] = A[K[i]] + C[M[i]]; Use index vector: LV Vk, Rk LVI Va, (Ra+Vk) LV Vm, Rm LVI Vc, (Rc+Vm) ADDVV. D Va, Vc SVI (Ra+Vk), Va ; load K ; load A[K[]] ; load M ; load C[M[]] ; add them ; store A[K[]] Copyright © 2012, Elsevier Inc. All rights reserved. 17

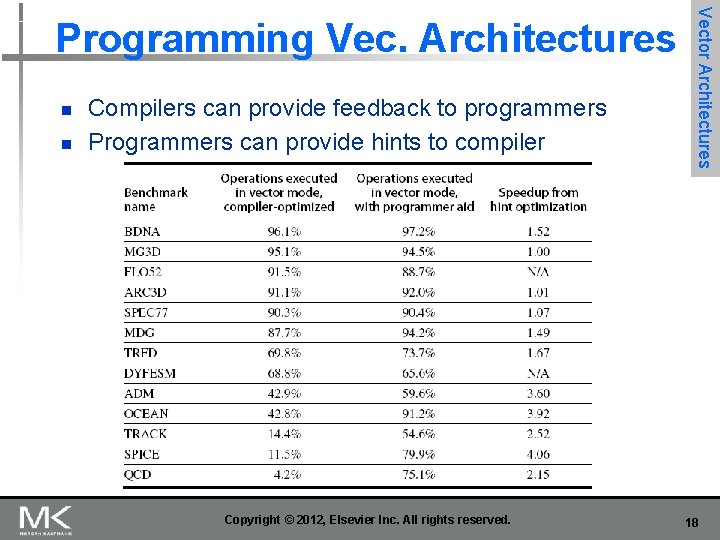
n n Compilers can provide feedback to programmers Programmers can provide hints to compiler Copyright © 2012, Elsevier Inc. All rights reserved. Vector Architectures Programming Vec. Architectures 18

n n Media applications operate on data types narrower than the native word size n Example: disconnect carry chains to “partition” adder Limitations, compared to vector instructions: n Number of data operands encoded into opcode (i. s. o. using VL register) n No sophisticated addressing modes (like strided, scatter-gather) n No mask registers Copyright © 2012, Elsevier Inc. All rights reserved. SIMD Instruction Set Extensions for Multimedia SIMD Extensions 19

n Implementations: n Intel MMX (1996) n n Streaming SIMD Extensions (SSE) (1999) n n n Eight 16 -bit integer ops Four 32 -bit integer/fp ops or two 64 -bit integer/fp ops Advanced Vector Extensions (AVX 2010) n n n Eight 8 -bit integer ops or four 16 -bit integer ops Four 64 -bit integer/fp ops 256 bit vectors -> 512 -> 1024 SIMD Instruction Set Extensions for Multimedia SIMD Implementations Operands must be consecutive and aligned memory locations Copyright © 2012, Elsevier Inc. All rights reserved. 20

n Example DXPY (Y=a*X + Y): L. D MOV MOV DADDIU Loop: MUL. 4 D ADD. 4 D S. 4 D DADDIU DSUBU BNEZ F 0, a F 1, F 0 F 2, F 0 F 3, F 0 R 4, Rx, #512 L. 4 D F 4, 0[Rx] F 4, F 0 F 8, 0[Ry] F 8, F 4 0[Ry], F 8 Rx, #32 Ry, #32 R 20, R 4, Rx R 20, Loop ; load scalar a ; copy a into F 1 for SIMD MUL ; copy a into F 2 for SIMD MUL ; copy a into F 3 for SIMD MUL ; last address to load ; load X[i], X[i+1], X[i+2], X[i+3] ; a×X[i], a×X[i+1], a×X[i+2], a×X[i+3] ; load Y[i], Y[i+1], Y[i+2], Y[i+3] ; a×X[i]+Y[i], . . . , a×X[i+3]+Y[i+3] ; store into Y[i], Y[i+1], Y[i+2], Y[i+3] ; increment index to X ; increment index to Y ; compute bound ; check if done Copyright © 2012, Elsevier Inc. All rights reserved. SIMD Instruction Set Extensions for Multimedia Example SIMD Code 21

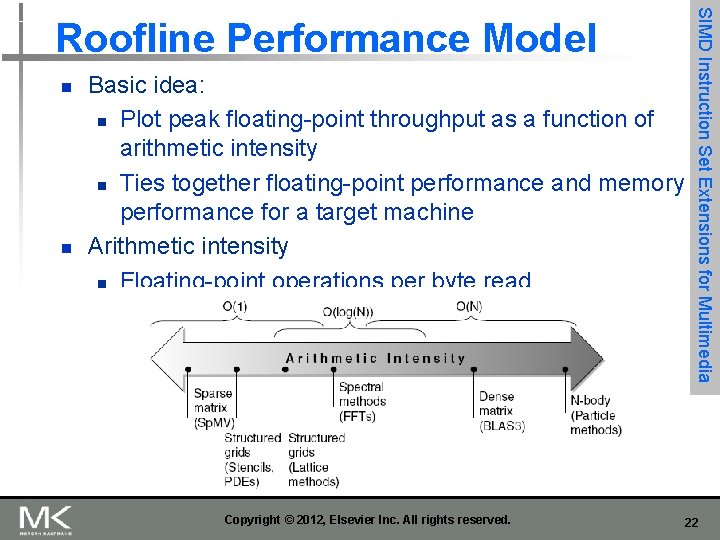
n n Basic idea: n Plot peak floating-point throughput as a function of arithmetic intensity n Ties together floating-point performance and memory performance for a target machine Arithmetic intensity n Floating-point operations per byte read Copyright © 2012, Elsevier Inc. All rights reserved. SIMD Instruction Set Extensions for Multimedia Roofline Performance Model 22

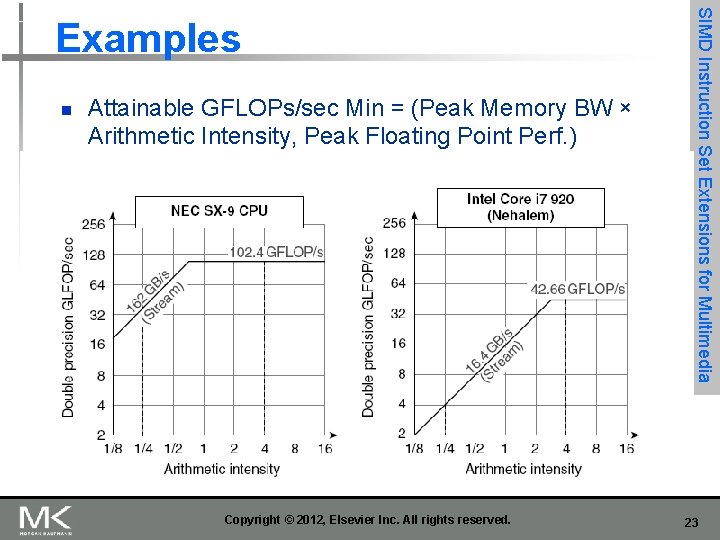
n Attainable GFLOPs/sec Min = (Peak Memory BW × Arithmetic Intensity, Peak Floating Point Perf. ) Copyright © 2012, Elsevier Inc. All rights reserved. SIMD Instruction Set Extensions for Multimedia Examples 23

n n Given the hardware invested to do graphics well, how can be supplement it to improve performance of a wider range of applications? Graphical Processing Units Basic idea: n Heterogeneous execution model n n CPU is the host, GPU is the device Develop a C-like programming language for GPU n n n NVIDIA: CUDA AMD/ATI: Brook+ Open. CL 24

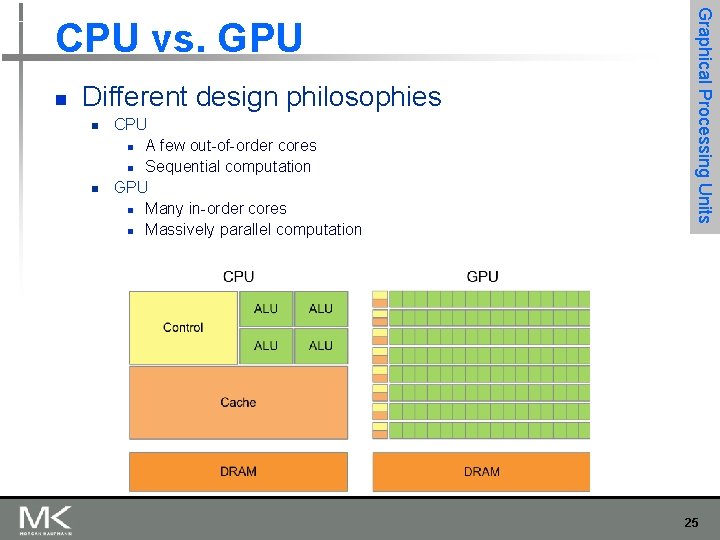
n Different design philosophies n n CPU n A few out-of-order cores n Sequential computation GPU n Many in-order cores n Massively parallel computation Graphical Processing Units CPU vs. GPU 25

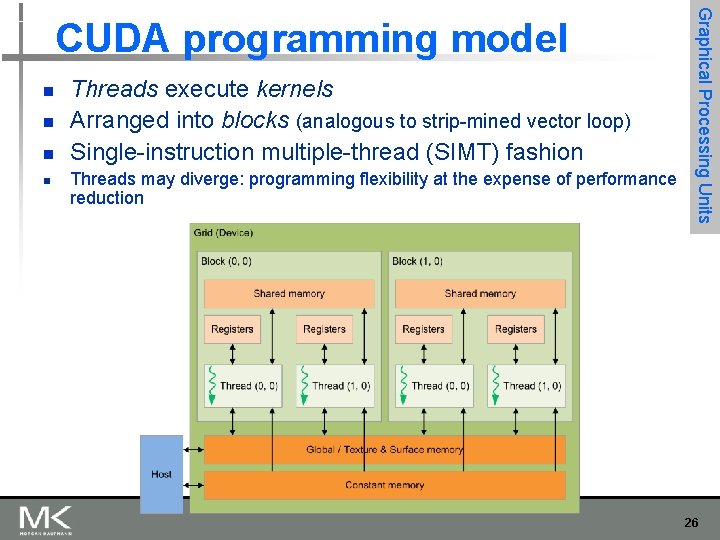
n n Threads execute kernels Arranged into blocks (analogous to strip-mined vector loop) Single-instruction multiple-thread (SIMT) fashion Threads may diverge: programming flexibility at the expense of performance reduction Graphical Processing Units CUDA programming model 26

n DAXPY: vectors of length 8192 n n Independent loop iterations Threads in thread blocks // DAXPY in C for (int i = 0; i < 8192; ++i) y[i] = a * x[i] + y[i]; Graphical Processing Units Example // DAXPY in CUDA – GPU code { int i = block. Idx. x * block. Dim. x + thread. Idx. x; if(i < n) y[i] = a * x[i] + y[i]; }. . . // Kernel invocation – CPU daxpy<<16, 512>>(n, a, x, y); 27

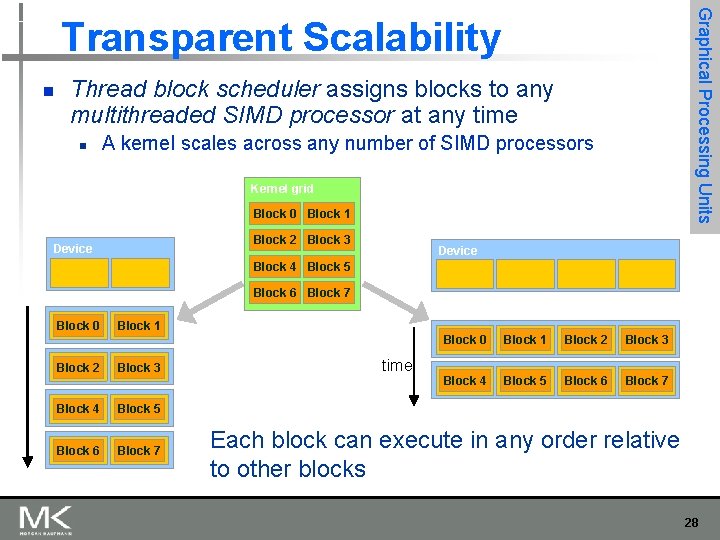
Graphical Processing Units Transparent Scalability n Thread block scheduler assigns blocks to any multithreaded SIMD processor at any time n A kernel scales across any number of SIMD processors Kernel grid Block 0 Block 1 Block 2 Block 3 Device Block 4 Block 5 Block 6 Block 7 Block 0 Block 2 Block 1 Block 3 Block 4 Block 5 Block 6 Block 7 Block 0 Block 1 Block 2 Block 3 Block 4 Block 5 Block 6 Block 7 time Each block can execute in any order relative to other blocks 28

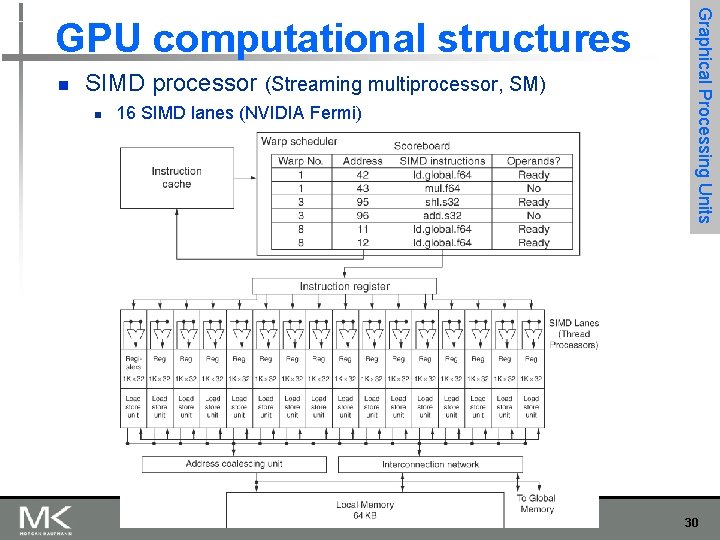
n Blocks within each SIMD processor: n n n SIMD lanes: 32 in NVIDIA devices Wide and shallow compared to vector processors Graphical Processing Units GPU computational structures Threads of SIMD instructions: Warps n n Each has its own PC SIMD thread scheduler uses scoreboard to dispatch No data dependencies between threads! Keeps track of up to 48 warps (Fermi) n Latency hiding 29

n SIMD processor (Streaming multiprocessor, SM) n 16 SIMD lanes (NVIDIA Fermi) Graphical Processing Units GPU computational structures 30

n SM hardware implements zero-overhead warp scheduling SIMD thread scheduler n time n warp 8 instruction 11 Operands ready? Eligible for execution Graphical Processing Units Scheduling of SIMD threads warp 1 instruction 42 warp 3 instruction 95. . . warp 8 instruction 12 warp 3 instruction 96 31 31

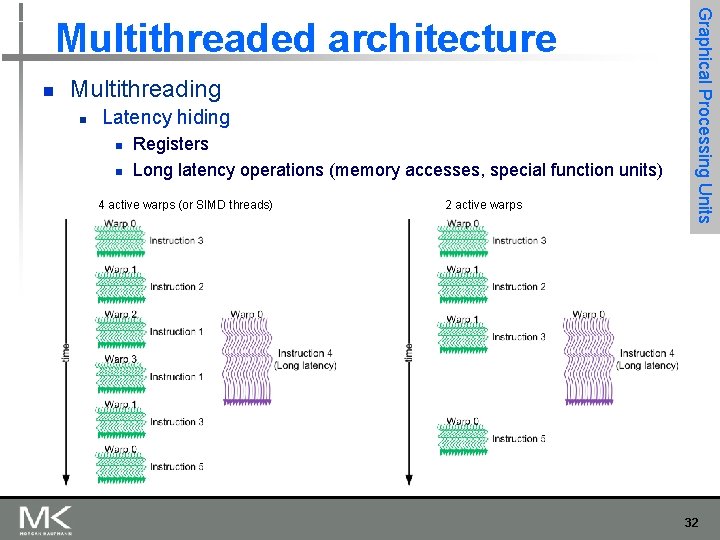
n Multithreading n Latency hiding n n Registers Long latency operations (memory accesses, special function units) 4 active warps (or SIMD threads) 2 active warps Graphical Processing Units Multithreaded architecture 32

n ISA is an abstraction of the hardware instruction set n n “Parallel Thread Execution (PTX)” Uses virtual registers Translation to machine code is performed in software Example: shl. s 32 R 8, block. Idx, 9 Graphical Processing Units NVIDIA Instruction Set Arch. ; Thread Block ID * Block size (512 or 29) add. s 32 R 8, thread. Idx ; R 8 = i = my CUDA thread ID ld. global. f 64 RD 0, [X+R 8] ; RD 0 = X[i] ld. global. f 64 RD 2, [Y+R 8] ; RD 2 = Y[i] mul. f 64 RD 0, RD 4 ; Product in RD 0 = RD 0 * RD 4 (scalar a) add. f 64 RD 0, RD 2 ; Sum in RD 0 = RD 0 + RD 2 (Y[i]) st. global. f 64 [Y+R 8], RD 0 ; Y[i] = sum (X[i]*a + Y[i]) 33

n n Like vector architectures, GPU branch hardware uses internal masks Also uses n Branch synchronization stack n n n Instruction markers to manage when a branch diverges into multiple execution paths n n Push on divergent branch …and when paths converge n n n Entries consist of masks for each SIMD lane I. e. which threads commit their results (all threads execute) Graphical Processing Units Conditional Branching Act as barriers Pops stack Per-thread-lane 1 -bit predicate register 34

if (X[i] != 0) X[i] = X[i] – Y[i]; else X[i] = Z[i]; ld. global. f 64 RD 0, [X+R 8] setp. neq. s 32 P 1, RD 0, #0 @!P 1, bra ELSE 1, *Push ld. global. f 64 RD 2, [Y+R 8] sub. f 64 RD 0, RD 2 st. global. f 64 [X+R 8], RD 0 @P 1, bra ENDIF 1, *Comp ELSE 1: ld. global. f 64 RD 0, [Z+R 8] st. global. f 64 [X+R 8], RD 0 ENDIF 1: <next instruction>, *Pop ; RD 0 = X[i] ; P 1 is predicate register 1 ; Push old mask, set new mask ; if P 1 false, go to ELSE 1 ; RD 2 = Y[i] ; Difference in RD 0 ; X[i] = RD 0 ; complement mask bits ; if P 1 true, go to ENDIF 1 ; RD 0 = Z[i] ; X[i] = RD 0 ; pop to restore old mask Graphical Processing Units Example 35

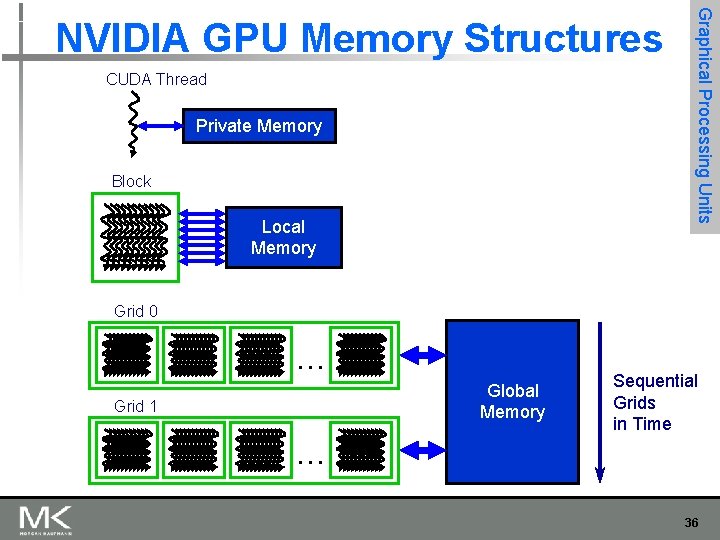
CUDA Thread Private Memory Block Local Memory Graphical Processing Units NVIDIA GPU Memory Structures Grid 0 . . . Global Memory Grid 1 Sequential Grids in Time . . . 36

n Each SIMD processor has n n n n n Two SIMD thread schedulers, two instruction dispatch units 16 SIMD lanes (SIMD width=32, chime=2 cycles), 16 load-store units, 4 special function units Thus, two threads of SIMD instructions are scheduled every two clock cycles Graphical Processing Units Fermi Architecture Innovations Fast double precision Caches for GPU memory: L 1, L 2 64 -bit addressing and unified address space Error correcting codes Faster context switching Faster atomic instructions 37

Graphical Processing Units Fermi Multithreaded SIMD Proc. 38

Graphical Processing Units Kepler Architecture Innovations n Each SIMD processor has n n n Compiler determines when instructions are ready to issue n n n 4 SIMD thread schedulers Each with 2 dispatch units – Instruction Level Parallelism 32 SIMD lanes for each SIMD thread (chime = 1 cycle) Thus, two instructions of 4 threads of SIMD instructions are scheduled every clock cycle This information is included in the instruction Even faster atomic instructions Shuffle instructions 39

Graphical Processing Units Kepler Multithreaded SIMD Proc. 40

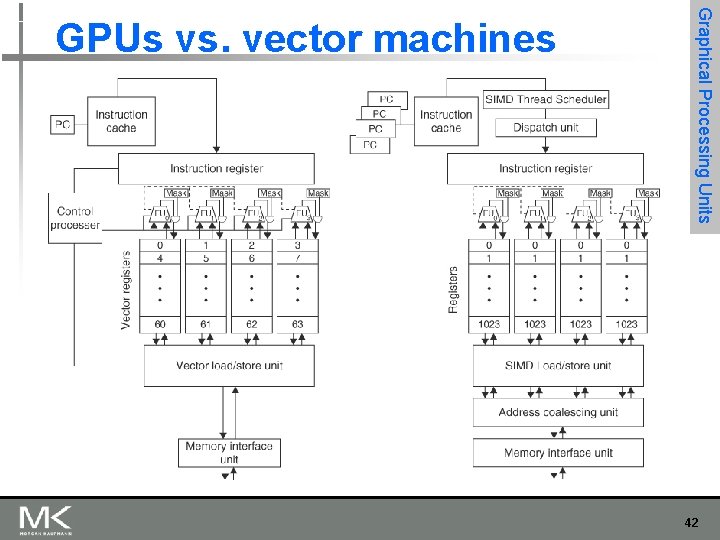
Graphical Processing Units GPUs vs. vector machines n Similarities to vector machines: n n n Works well with data-level parallel problems Scatter-gather transfers Mask registers Large register files Differences: n n n No scalar processor Uses multithreading to hide memory latency Has many functional units, as opposed to a few deeply pipelined units like a vector processor 41

Graphical Processing Units GPUs vs. vector machines 42

n Focuses on determining whether data accesses in later iterations are dependent on data values produced in earlier iterations n n Loop-carried dependence Example 1: for (i=999; i>=0; i=i-1) x[i] = x[i] + s; n No loop-carried dependence Detecting and Enhancing Loop-Level Parallelism 43

n Example 2: for (i=0; i<100; i=i+1) { A[i+1] = A[i] + C[i]; /* S 1 */ B[i+1] = B[i] + A[i+1]; /* S 2 */ } n n S 1 and S 2 use values computed by S 1 in previous iteration S 2 uses value computed by S 1 in same iteration Detecting and Enhancing Loop-Level Parallelism 44

n Example 3: for (i=0; i<100; i=i+1) { A[i] = A[i] + B[i]; /* S 1 */ B[i+1] = C[i] + D[i]; /* S 2 */ } n n S 1 uses value computed by S 2 in previous iteration but dependence is not circular so loop is parallel Transform to: A[0] = A[0] + B[0]; for (i=0; i<99; i=i+1) { B[i+1] = C[i] + D[i]; A[i+1] = A[i+1] + B[i+1]; } B[100] = C[99] + D[99]; Detecting and Enhancing Loop-Level Parallelism 45

n Assume indices are affine: n n n a x i + b (i is loop index) X[a x i + b] Assume: n n Store to a x i + b, then Load from c x i + d i runs from m to n Dependence exists if: n n Detecting and Enhancing Loop-Level Parallelism Finding dependencies Given j, k such that m ≤ j ≤ n, m ≤ k ≤ n Store to a x j + b, load from c x k + d, and a x j + b = c x k + d 46

n n Generally cannot determine at compile time Test for absence of a dependence: n GCD test: n n If a dependency exists, GCD(c, a) must evenly divide (d-b) Example: for (i=0; i<100; i=i+1) { X[2*i+3] = X[2*i] * 5. 0; } n n a=2, b=3, c=2, d=0 d-b=-3, GCD(a, c)=2 Detecting and Enhancing Loop-Level Parallelism Finding dependencies 47

n Example 2: for (i=0; i<100; i=i+1) { Y[i] = X[i] / c; /* S 1 */ X[i] = X[i] + c; /* S 2 */ Z[i] = Y[i] + c; /* S 3 */ Y[i] = c - Y[i]; /* S 4 */ } n Watch for antidependencies and output dependencies for (i=0; i<100; i=i+1) { T[i] = X[i] / c; /* S 1 */ X 1[i] = X[i] + c; /* S 2 */ Z[i] = T[i] + c; /* S 3 */ Y[i] = c - T[i]; /* S 4 */ } Detecting and Enhancing Loop-Level Parallelism Finding dependencies 48

n Reduction Operation: for (i=9999; i>=0; i=i-1) sum = sum + x[i] * y[i]; n Transform to… for (i=9999; i>=0; i=i-1) sum [i] = x[i] * y[i]; for (i=9999; i>=0; i=i-1) finalsum = finalsum + sum[i]; n Do on p processors: for (i=999; i>=0; i=i-1) finalsum[p] = finalsum[p] + sum[i+1000*p]; n Detecting and Enhancing Loop-Level Parallelism Reductions Note: assumes associativity! 49

n Increasing importance of data-level parallelism n n n Personal mobile devices Audio, video, games GPUs tend to become more mainstream n n n Graphical Processing Units Concluding remarks Small size of GPU memory CPU-GPU transfers Unified physical memories n AMD Fusion 50