Computer Architecture A Constructive Approach Sequential Circuits Arvind

Computer Architecture: A Constructive Approach Sequential Circuits Arvind Computer Science & Artificial Intelligence Lab. Massachusetts Institute of Technology Revised February 21, 2012 (Slides from #16 onwards) February 15, 2012 http: //csg. csail. mit. edu/6. S 078 L 3 -1

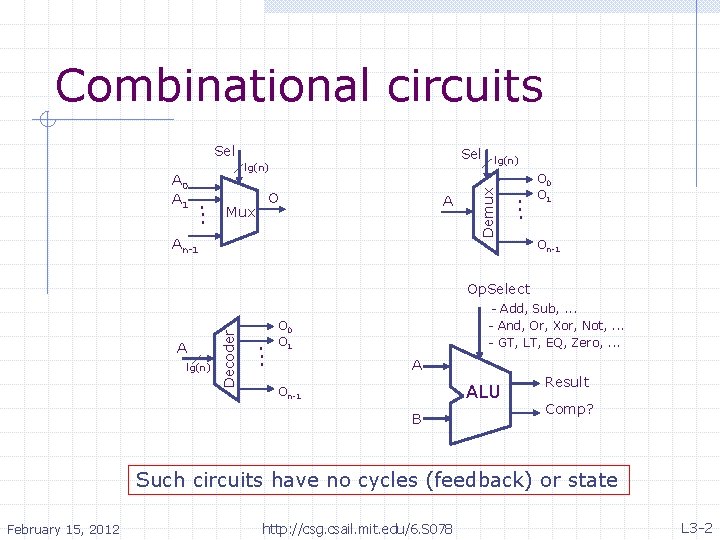
Combinational circuits Sel . . . O Mux A An-1 lg(n) Demux A 0 A 1 Sel lg(n) . . . O 0 O 1 On-1 A lg(n) Decoder Op. Select . . . - Add, Sub, . . . - And, Or, Xor, Not, . . . - GT, LT, EQ, Zero, . . . O 0 O 1 A ALU On-1 B Result Comp? Such circuits have no cycles (feedback) or state February 15, 2012 http: //csg. csail. mit. edu/6. S 078 L 3 -2

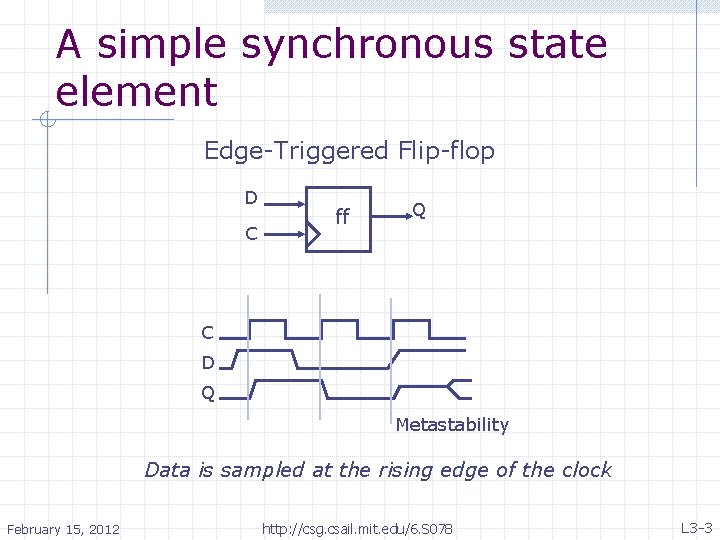
A simple synchronous state element Edge-Triggered Flip-flop D C ff Q C D Q Metastability Data is sampled at the rising edge of the clock February 15, 2012 http: //csg. csail. mit. edu/6. S 078 L 3 -3

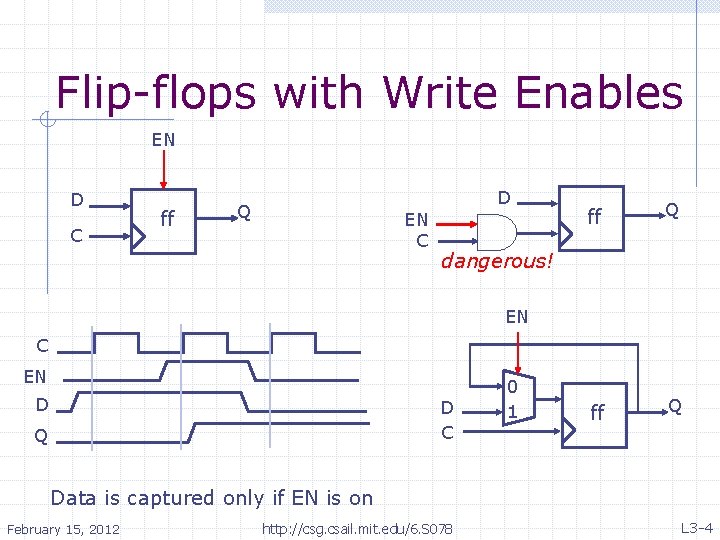
Flip-flops with Write Enables EN D C ff D Q EN C ff Q dangerous! EN C EN D D C Q 0 1 Data is captured only if EN is on February 15, 2012 http: //csg. csail. mit. edu/6. S 078 L 3 -4

Registers D D D D ff ff Q Q Q Q En C Register: A group of flip-flops with a common clock and enable Register file: A group of registers with a common clock, input and output port(s) February 15, 2012 http: //csg. csail. mit. edu/6. S 078 L 3 -5

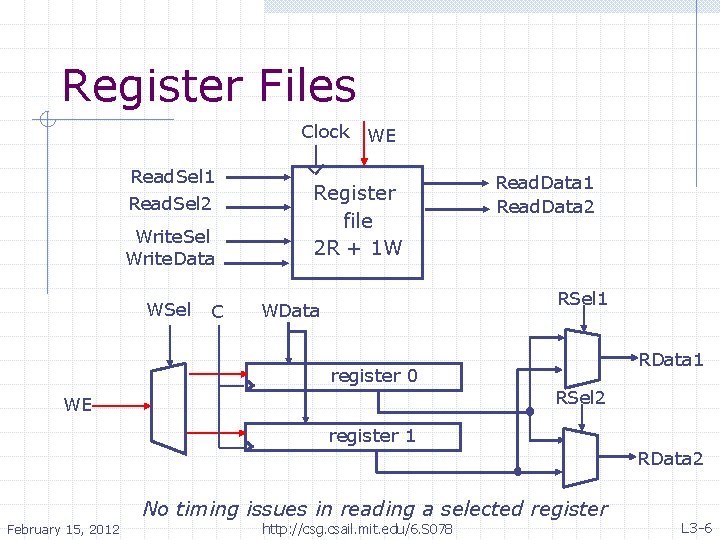
Register Files Clock WE Read. Sel 1 Read. Sel 2 Write. Sel Write. Data WSel C Register file 2 R + 1 W Read. Data 1 Read. Data 2 RSel 1 WData RData 1 register 0 RSel 2 WE register 1 RData 2 No timing issues in reading a selected register February 15, 2012 http: //csg. csail. mit. edu/6. S 078 L 3 -6

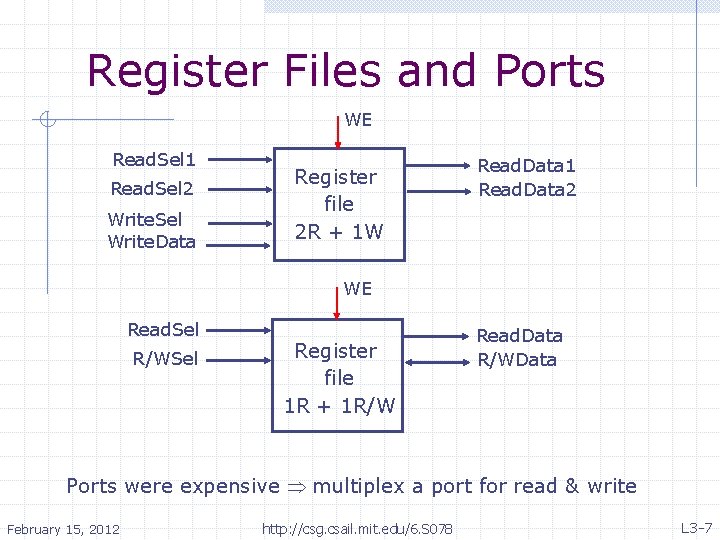
Register Files and Ports WE Read. Sel 1 Read. Sel 2 Write. Sel Write. Data Register file 2 R + 1 W Read. Data 1 Read. Data 2 WE Read. Sel R/WSel Register file 1 R + 1 R/W Read. Data R/WData Ports were expensive multiplex a port for read & write February 15, 2012 http: //csg. csail. mit. edu/6. S 078 L 3 -7

We can build useful and compact circuits using registers Example: Multiplication by repeated addition February 15, 2012 http: //csg. csail. mit. edu/6. S 078 L 3 -8

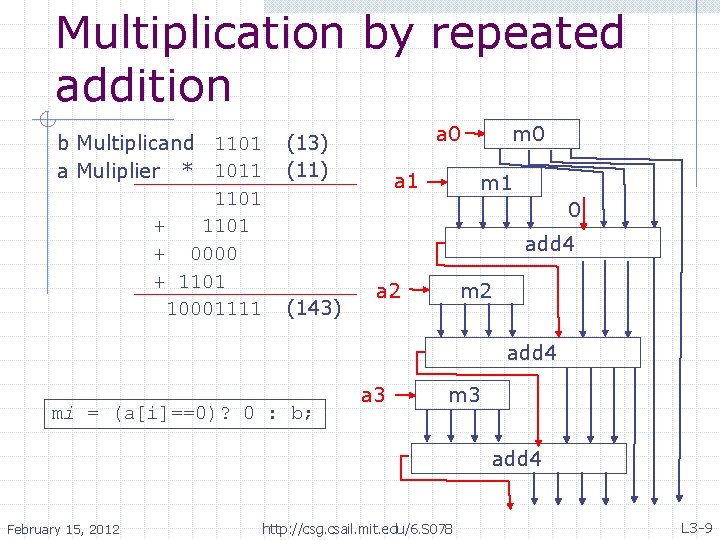
Multiplication by repeated addition b Multiplicand 1101 a Muliplier * 1011 1101 + 0000 + 1101 10001111 a 0 (13) (11) a 1 m 0 m 1 0 add 4 (143) a 2 m 2 add 4 mi = (a[i]==0)? 0 : b; a 3 m 3 add 4 February 15, 2012 http: //csg. csail. mit. edu/6. S 078 L 3 -9

Combinational 32 -bit multiply function Bit#(64) mul 32(Bit#(32) a, Bit#(32) b); Bit#(32) prod = 0; Bit#(32) tp = 0; for(Integer i = 0; i < 32; i = i+1) begin Bit#(32) m = (a[i]==0)? 0 : b; Bit#(33) sum = add 32(m, tp, 0); prod[i] = sum[0]; tp = truncate. LSB(sum); end return {tp, prod}; endfunction February 15, 2012 http: //csg. csail. mit. edu/6. S 078 L 3 -10

Design issues with combinational multiply Lot of hardware n 32 -bit multiply uses 31 add. N circuits Long chains of gates n n 32 -bit ripple carry adder has a 31 long chain of gates 32 -bit multiply has 31 ripple carry adders in sequence! The speed of a combinational circuit is determined by its longest input-to-output path February 15, 2012 http: //csg. csail. mit. edu/6. S 078 L 3 -11

Expressing a loop using registers function Bit#(64) mul 32(Bit#(32) a, Bit#(32) b); Bit#(32) prod = 0; Bit#(32) tp = 0; for(Integer i = 0; i < 32; i = i+1) begin Bit#(32) m = (a[i]==0)? 0 : b; Bit#(33) sum = add 32(m, tp, 0); prod[i] = sum[0]; tp = truncate. LSB(sum); end return {tp, prod}; endfunction Need registers to hold a, b, tp prod and i Update the registers every cycle until we are done February 15, 2012 http: //csg. csail. mit. edu/6. S 078 L 3 -12

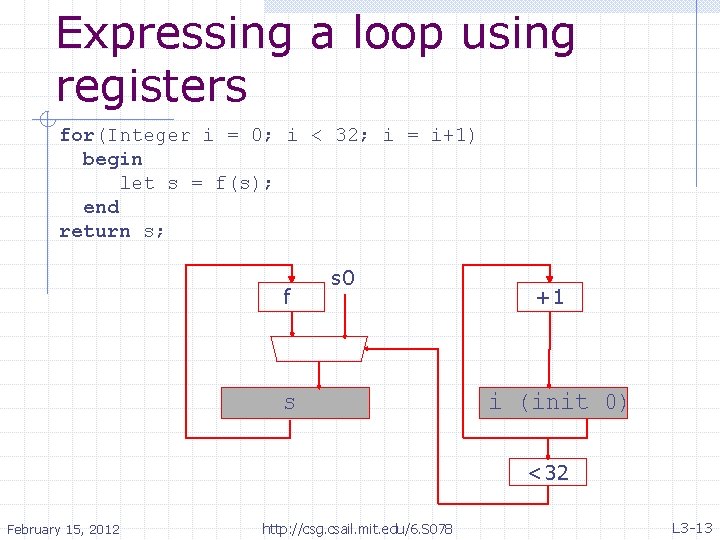
Expressing a loop using registers for(Integer i = 0; i < 32; i = i+1) begin let s = f(s); end return s; • f • s 0 s +1 i (init 0) <32 February 15, 2012 http: //csg. csail. mit. edu/6. S 078 L 3 -13

Sequential multiply Reg#(Bit#(32)) Reg#(Bit#(6)) a <- mk. Reg. U(); b <- mk. Reg. U(); prod <-mk. Reg. U(); tp <- mk. Reg. U(); i <- mk. Reg(32); rule mul. Step if (i < 32); Bit#(32) m = (a[i]==0)? 0 : b; Bit#(33) sum = add 32(m, tp, 0); prod[i] <= sum[0]; tp <= sum[32: 1]; i <= i+1; endrule state elements a rule to describe dynamic behavior So that the rule won’t fire until i is set to some other value February 15, 2012 http: //csg. csail. mit. edu/6. S 078 L 3 -14

Dynamic selection requires a mux i a a[i] • >> a 0 February 15, 2012 http: //csg. csail. mit. edu/6. S 078 a[0], a[1], a[2], … L 3 -15

Replacing repeated selections by shifts Reg#(Bit#(32)) Reg#(Bit#(6)) a <- mk. Reg. U(); b <- mk. Reg. U(); prod <-mk. Reg. U(); tp <- mk. Reg. U(); i <- mk. Reg(32); rule mul. Step if (i < 32); Bit#(32) m = (a[0]==0)? 0 : b; a <= a >> 1; Bit#(33) sum = add 32(m, tp, 0); prod <= {sum[0], (prod >> 1)[30: 0]}; tp <= sum[32: 1]; i <= i+1; endrule February 15, 2012 http: //csg. csail. mit. edu/6. S 078 L 3 -16

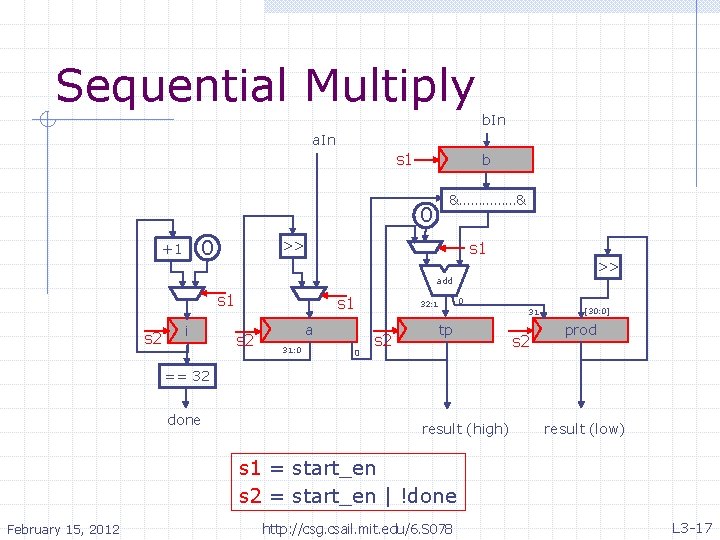
Sequential Multiply b. In a. In s 1 b &……………& 0 0 << s 1 << +1 add s 1 s 2 i s 1 s 2 a 31: 0 0 32: 1 s 2 0 tp 31 s 2 [30: 0] prod == 32 done result (high) result (low) s 1 = start_en s 2 = start_en | !done February 15, 2012 http: //csg. csail. mit. edu/6. S 078 L 3 -17

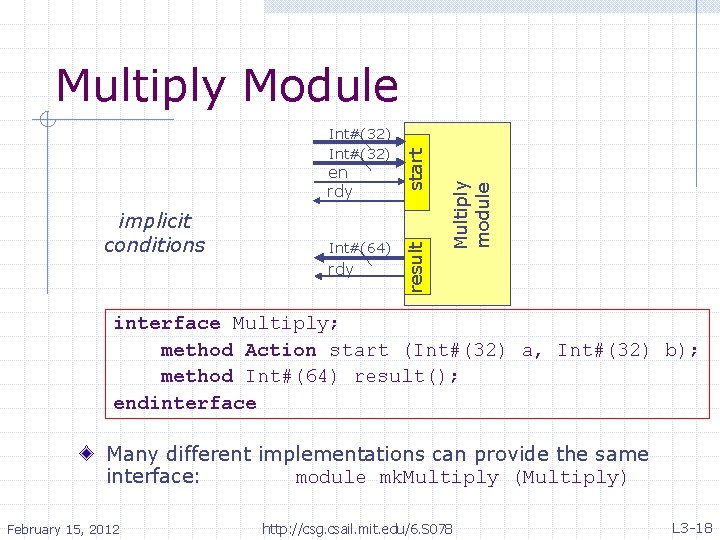
implicit conditions Int#(64) rdy Multiply module en rdy result Int#(32) start Multiply Module interface Multiply; method Action start (Int#(32) a, Int#(32) b); method Int#(64) result(); endinterface Many different implementations can provide the same interface: module mk. Multiply (Multiply) February 15, 2012 http: //csg. csail. mit. edu/6. S 078 L 3 -18

External interface Multiply Module mk. Multiply 32 (Multiply 32); Reg#(Bit#(32)) a <- mk. Reg. U(); Reg#(Bit#(32)) b <- mk. Reg. U(); Reg#(Bit#(32)) prod <-mk. Reg. U(); State Reg#(Bit#(32)) tp <- mk. Reg. U(); Reg#(Bit#(6)) i <- mk. Reg(32); rule mul. Step if (i < 32); Bit#(32) m = (a[0]==0)? 0 : b; Internal Bit#(33) sum = add 32(m, tp, 0); behavior prod <= {sum[0], (prod >> 1)[30: 0]}; tp <= sum[32: 1]; a <= a >> 1; i <= i+1; endrule method Action start(Bit#(32) a. In, Bit#(32) b. In) if (i == 32); a <= a. In; b <= b. In; i <= 0; tp <= 0; prod <= 0; endmethod Bit#(64) result() if (i == 32); return {tp, prod}; endmethod endmodule February 15, 2012 http: //csg. csail. mit. edu/6. S 078 L 3 -19

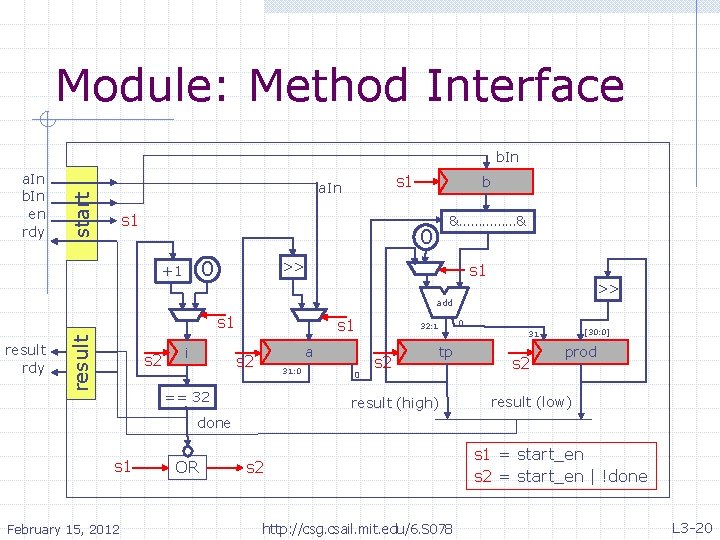
Module: Method Interface b. In s 1 b &……………& 0 0 +1 s 1 << start a. In << a. In b. In • en rdy add result rdy result s 1 s 2 i s 1 a s 2 31: 0 == 32 0 32: 1 s 2 tp result (high) 0 [30: 0] 31 s 2 prod result (low) done s 1 February 15, 2012 OR s 2 http: //csg. csail. mit. edu/6. S 078 s 1 = start_en s 2 = start_en | !done L 3 -20

Polymorphic Multiply Module Tadd(n+n) Int#(64) rdy #(Numeric type n) result implicit conditions n could be Multiply module enab rdy start n Int#(32), Int#(13), . . . interface Multiply; n n method Action start (Int#(32) a, Int#(32) b); TAdd#(n, n) method Int#(64) result(); endinterface The module can easily be made polymorphic January 11, 2012 http: //csg. csail. mit. edu/SNU L 02 -21

Sequential n-bit multiply module mk. Multiply. N (Multiply. N); Reg#(Bit#(n)) a <- mk. Reg. U(); Reg#(Bit#(n)) b <- mk. Reg. U(); Reg#(Bit#(n)) prod <-mk. Reg. U(); Reg#(Bit#(n)) tp <- mk. Reg. U(); Reg#(Bit#(Add#(Tlog(n), 1)) i <- mk. Reg(n); nv = value. Of(n); rule mul. Step if (i < nv); Bit#(n) m = (a[0]==0)? 0 : b; Bit#(TAdd#(n, 1)) sum = addn(m, tp, 0); prod <= {sum[0], (prod >> 1)[(nv-2): 0]}; tp <= sum[n: 1]; a <= a >> 1; i <= i+1; endrule method Action start(Bit#(n) a. In, Bit#(n) b. In) if (i == nv); a <= a. In; b <= b. In; i <= 0; tp <= 0; prod <= 0; endmethod Bit#(TAdd#(n, n)) result() if (i == nv); return {tp, prod}; endmethod endmodule February 15, 2012 http: //csg. csail. mit. edu/6. S 078 L 3 -22