Computer Architecture A Constructive Approach Instruction Representation Arvind

Computer Architecture: A Constructive Approach Instruction Representation Arvind Computer Science & Artificial Intelligence Lab. Massachusetts Institute of Technology January 13, 2012 http: //csg. csail. mit. edu/SNU L 5 -1

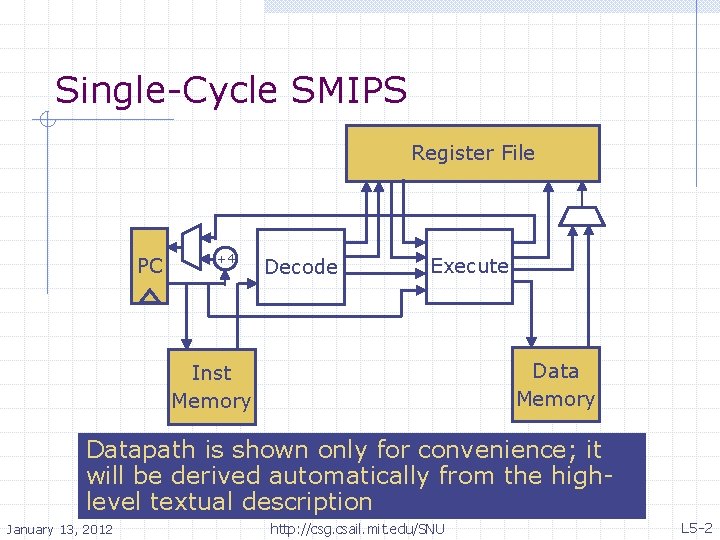
Single-Cycle SMIPS Register File PC +4 Decode Execute Data Memory Inst Memory Datapath is shown only for convenience; it will be derived automatically from the highlevel textual description January 13, 2012 http: //csg. csail. mit. edu/SNU L 5 -2

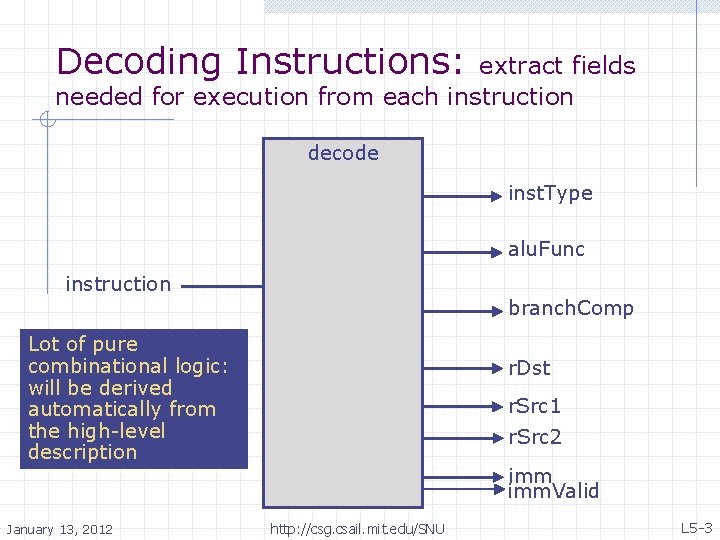
Decoding Instructions: extract fields needed for execution from each instruction decode 31: 26 inst. Type 31: 26 alu. Func 5: 0 instruction Lot of pure combinational logic: will be derived automatically from the high-level description 31: 26 20: 16 r. Dst 15: 11 25: 21 r. Src 1 20: 16 r. Src 2 15: 0 25: 0 January 13, 2012 branch. Comp ext http: //csg. csail. mit. edu/SNU imm. Valid L 5 -3

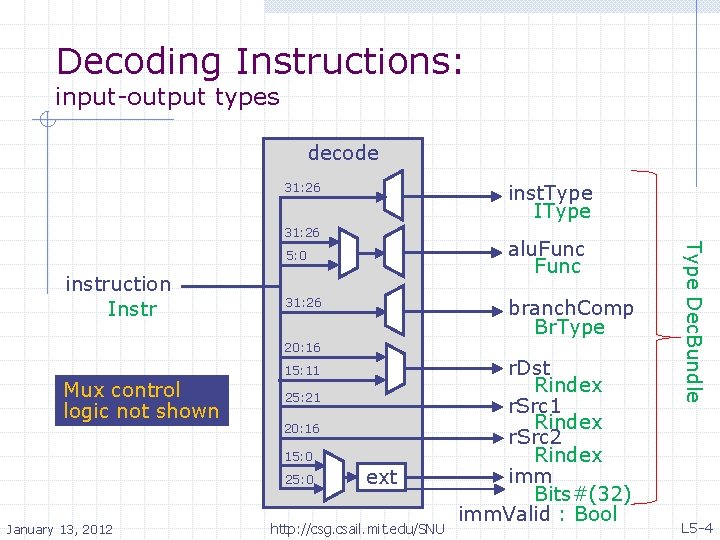
Decoding Instructions: input-output types decode 31: 26 inst. Type IType 31: 26 instruction Instr 31: 26 branch. Comp Br. Type 20: 16 Mux control logic not shown 15: 11 25: 21 20: 16 15: 0 25: 0 January 13, 2012 ext http: //csg. csail. mit. edu/SNU r. Dst Rindex r. Src 1 Rindex r. Src 2 Rindex imm Bits#(32) imm. Valid : Bool Type Dec. Bundle alu. Func 5: 0 L 5 -4

Type defs typedef enum {RAlu, IALU, Ld, St, …} IType deriving(Bits, Eq); typedef enum {Eq, Neq, Le, Lt, Ge, Gt, J, JR, N} Br. Type deriving(Bits, Eq); typedef enum {Add, Sub, And, Or, Xor, Nor, Sltu, LShift, RShift, Sra} Func deriving(Bits, Eq); January 13, 2012 http: //csg. csail. mit. edu/SNU L 5 -5

Instruction grouping Many instructions have the same implementation except for the ALU function they invoke We can group such instructions and reduce the amount of code we have to write Example: R-Type ALU, I-Type ALU, Br Type, Memory Type, … January 13, 2012 http: //csg. csail. mit. edu/SNU L 5 -6

Decoding Instructions function Decoded. Inst decode(Bit#(32) inst, Addr pc); Decoded. Inst = ? ; let opcode = instr. Bits[ 31 : 26 ]; let rs = instr. Bits[ 25 : 21 ]; let rt = instr. Bits[ 20 : 16 ]; let rd = instr. Bits[ 15 : 11 ]; let shamt = instr. Bits[ 10 : 6 ]; let funct = instr. Bits[ 5 : 0 ]; let imm = instr. Bits[ 15 : 0 ]; let target = instr. Bits[ 25 : 0 ]; case (inst. Type(opcode)). . . endcase return d. Inst; endfunction January 13, 2012 http: //csg. csail. mit. edu/SNU L 5 -7

Decoding Instructions: R-Type ALU case (inst. Type(opcode)) … RAlu: begin d. Inst. inst. Type = Alu; d. Inst. alu. Func = case (funct) fc. ADDU: Add fc. SUBU: Sub. . . endcase; d. Inst. r. Dst = rd; d. Inst. r. Src 1 = rs; d. Inst. r. Src 2 = rt; d. Tnst. imm. Valid = False end January 13, 2012 http: //csg. csail. mit. edu/SNU L 5 -8

Decoding Instructions: I-Type ALU case (inst. Type(opcode)) … IAlu: begin d. Inst. inst. Type = Alu; d. Inst. alu. Func = case (opcode) op. ADDUI: Add. . . endcase; d. Inst. r. Dst = rt; d. Inst. r. Src 1 = rs; d. Inst. imm = signed. IAlu(opcode) ? sign. Extend(imm): zero. Extend(imm); d. Tnst. imm. Valid = True end January 13, 2012 http: //csg. csail. mit. edu/SNU L 5 -9

Decoding Instructions: Load & Store case (inst. Type(opcode)) LW: begin d. Inst. inst. Type = Ld; d. Inst. alu. Func = Add; d. Inst. r. Dst = rt; d. Inst. r. Src 1 = rs; d. Inst. imm = sign. Extned(imm); d. Tnst. imm. Valid = True end SW: begin d. Inst. inst. Type = St; d. Inst. alu. Func = Add; d. Inst. r. Dst = rt; d. Inst. r. Src 1 = rs; d. Inst. imm = sign. Extned(imm); d. Tnst. imm. Valid = True end January 13, 2012 http: //csg. csail. mit. edu/SNU L 5 -10

Decoding Instructions: Jump case (inst. Type(opcode)) … J, JAL: begin d. Inst. inst. Type = opcode==J ? J : Jal; d. Inst. r. Dst = 31; d. Inst. imm = zero. Extend({target, 2’b 00}); d. Tnst. imm. Valid = True end r. Jump: begin d. Inst. inst. Type = funct==JR ? Jr : Jalr; d. Inst. r. Dst = rd; d. Inst. r. Src 1 = rs; end January 13, 2012 http: //csg. csail. mit. edu/SNU L 5 -11

Decoding Instructions: Branch case (inst. Type(opcode)) … Branch: begin d. Inst. inst. Type = Br; d. Inst. branch. Comp = case (opcode) op. BEQ: EQ op. BLEZ: LE. . . endcase; d. Inst. r. Src 1 = rs; d. Inst. r. Src 2 = rt; d. Inst. imm = sign. Extend({imm, 2’b 00}); d. Tnst. imm. Valid = True end January 13, 2012 http: //csg. csail. mit. edu/SNU L 5 -12

Decoding Not all fields of d. Inst are defined in each case We may decide to pass more information from decode to execute for efficiency– in that case the definition of the type of the decoded instruction has to be adjusted accordingly January 13, 2012 http: //csg. csail. mit. edu/SNU L 5 -13

Single-Cycle SMIPS module mk. Proc(Proc); Reg#(Addr) pc <- mk. Reg. U; RFile rf <- mk. RFile; Memory mem <- mk. Memory; rule fetch. And. Execute; //fetch let inst. Resp <mem. iside(Mem. Req{op: Ld, addr: pc, data: ? }); //decode let dec. Inst = decode(inst. Resp); Data r. Val 1 = rf. rd 1(dec. Inst. r. Src 1); Data r. Val 2 = rf. rd 2(dec. Inst. r. Src 2); January 13, 2012 http: //csg. csail. mit. edu/SNU L 5 -14 • 14

• Single-Cycle SMIPS cont //execute let exec. Inst = exec(dec. Inst, pc, r. Val 1, r. Val 2); if(exec. Inst. inst. Type==Ld || exec. Inst. inst. Type==St) exec. Inst. data <- mem. dside( Mem. Req{op: exec. Inst. inst. Type, addr: exec. Inst. addr, data: exec. Inst. data}); pc <= exec. Inst. br. Taken ? exec. Inst. addr : pc + 4; //writeback if(exec. Inst. inst. Type==Alu || exec. Inst. inst. Type==Ld) rf. wr(exec. Inst. r. Dst, exec. Inst. data); endrule endmodule; January 13, 2012 http: //csg. csail. mit. edu/SNU L 5 -15

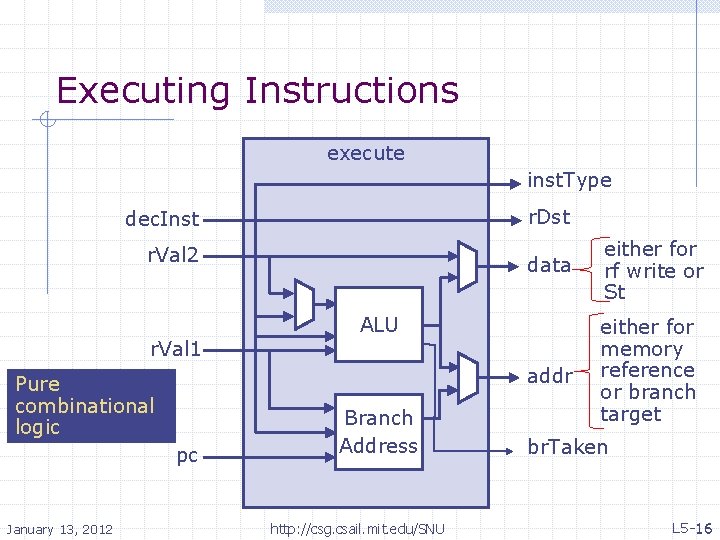
Executing Instructions execute inst. Type r. Dst dec. Inst r. Val 2 data either for rf write or St addr either for memory reference or branch target ALU r. Val 1 Pure combinational logic pc January 13, 2012 Branch Address http: //csg. csail. mit. edu/SNU br. Taken L 5 -16 • 16

Executing Instructions function Exec. Inst exec(Decoded. Inst, Addr pc, Data r. Val 1, Data r. Val 2); Data alu. Val 2 = (d. Inst. imm. Valid)? d. Inst. imm : r. Val 2 let alu. Res = alu(r. Val 1, alu. Val 2, d. Inst. alu. Func); let br. Res = alu. Br(r. Val 1, alu. Val 2, d. Inst. br. Comp); let br. Addr = br. Addr. Cal(pc, r. Val 1, d. Inst. inst. Type, d. Inst. imm); return Exec. Inst{ inst. Type: d. Inst. inst. Type, br. Taken: br. Res, addr: d. Inst. inst. Type==(Ld || St) ? alu. Res : br. addr, data: d. Inst. inst. Type==St ? r. Val 2 : alu. Res, r. Dst: d. Inst. r. Dst}; endfunction January 13, 2012 http: //csg. csail. mit. edu/SNU L 5 -17 • 17

Branch Resolution function Address br. Addr. Cal(Address pc, Data val, Inst. Type i. Type, Data imm); let target. Addr = case (i. Type) J : {pc[31: 26], imm[25: 0]} JR : val default: pc + imm endcase; return target. Addr; endfunction January 13, 2012 http: //csg. csail. mit. edu/SNU L 5 -18 • 18

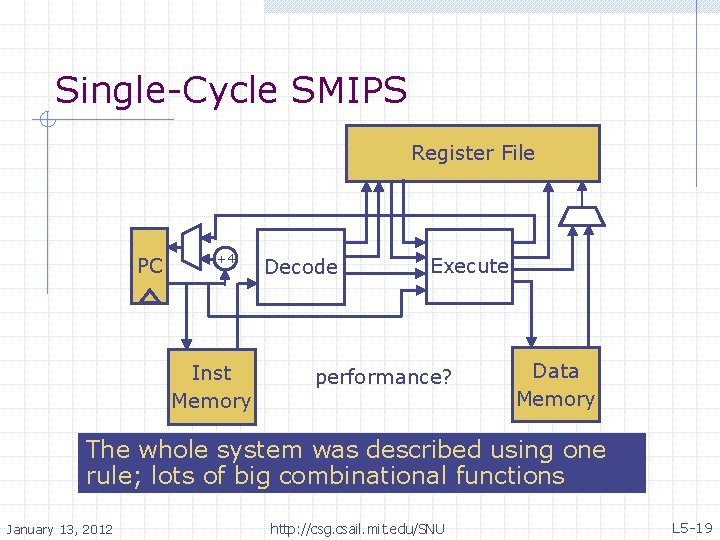
Single-Cycle SMIPS Register File PC +4 Inst Memory Decode Execute performance? Data Memory The whole system was described using one rule; lots of big combinational functions January 13, 2012 http: //csg. csail. mit. edu/SNU L 5 -19

Next few lectures Can we build a faster machine? What if program and data resided in the same memory What if the register file did not have adequate number of ports January 13, 2012 http: //csg. csail. mit. edu/SNU L 5 -20