Computer Architecture A Constructive Approach Combinational ALU Arvind

Computer Architecture: A Constructive Approach Combinational ALU Arvind Computer Science & Artificial Intelligence Lab. Massachusetts Institute of Technology January 9, 2012 http: //csg. csail. mit. edu/SNU L 1 -1

Computing Devices Then… EDSAC, University of Cambridge, UK, 1949 January 9, 2012 http: //csg. csail. mit. edu/SNU L 01 -2

Computing Devices Now Dramatic progress in terms of size, speed, cost, reliability January 9, 2012 http: //csg. csail. mit. edu/SNU L 01 -3

How does a program execute on hardware A C program to add two arrays: void vvadd( int n, int a[], int b[], int c[] ) { int i; for ( i = 0; i < n; i++ ) c[i] = a[i] + b[i]; } The hardware must know, for example, n n How to add and compare two numbers Must have a place to keep the program and data Must know how to fetch instructions and data Must know how to sequence instructions: w Fetch a[i], Fetch b[i], add, store results in c[i], increment i, … Computer Architecture is learning about how programs execute and designing hardware to execute them efficiently January 9, 2012 http: //csg. csail. mit. edu/SNU L 1 -4

Instruction Set Architecture (ISA) Computer architecture is the discipline of designing and implementing interfaces through which hardware and software interact This interface is often referred to as the Instruction Set Architecture (ISA) n n Examples: Intel’s IA-32, ARM-Thumb, Power. PC In this class we will use SMIPS, a subset of MIPS ISA Implementations are deeply affected by the technology issues; we will assume a simple and abstract model of technology based on Silicon January 9, 2012 http: //csg. csail. mit. edu/SNU L 1 -5

Goal of the Intensive Course Learn a constructive approach to studying computer architecture Learn a new method of describing architectures where there is less emphasis on figures/diagrams and more emphasis on executable descriptions n Each architecture and each part of it would be defined as executable code in Bluespec By this Friday you will have designed several different computers on which you will be able to execute your C programs January 9, 2012 http: //csg. csail. mit. edu/SNU L 1 -6

In this lecture we will study how to implement simple arithmetic-logic operations we will first look at circuits for component functions such as Add, Shift and then put them together to form an Arithmetic-Logic Unit (ALU) January 9, 2012 http: //csg. csail. mit. edu/SNU L 1 -7

Arithmetic-Logic Unit (ALU) Computers have many important interconnected parts or subsystems: n n n Central Processing Unit Memory system including caches I/O systems Op ALU resides inside the CPU and carried out all the arithmetic and logical functions January 9, 2012 A - Add, Sub, . . . - And, Or, Xor, Not, . . . - GT, LT, EQ, Zero, . . . • ALU B http: //csg. csail. mit. edu/SNU Result Comp? L 1 -8
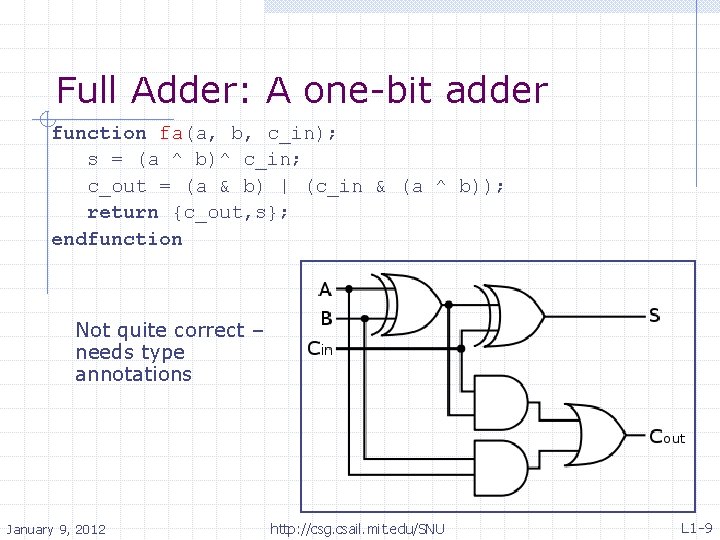
Full Adder: A one-bit adder function fa(a, b, c_in); s = (a ^ b)^ c_in; c_out = (a & b) | (c_in & (a ^ b)); return {c_out, s}; endfunction Not quite correct – needs type annotations January 9, 2012 http: //csg. csail. mit. edu/SNU L 1 -9
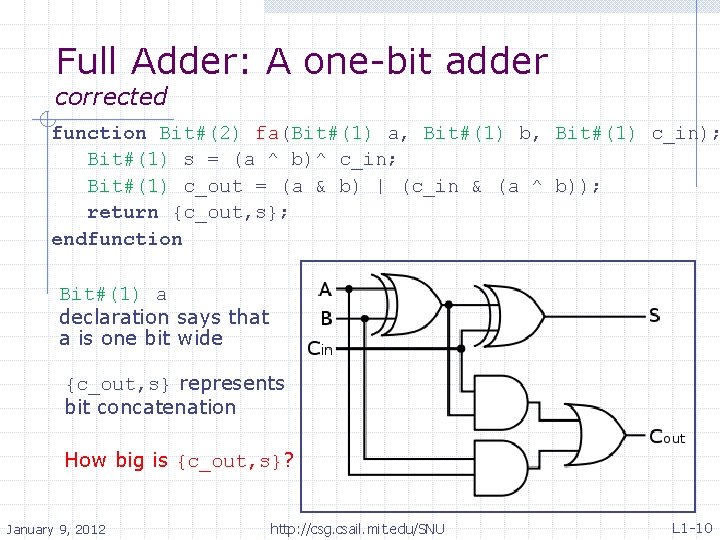
Full Adder: A one-bit adder corrected function Bit#(2) fa(Bit#(1) a, Bit#(1) b, Bit#(1) c_in); Bit#(1) s = (a ^ b)^ c_in; Bit#(1) c_out = (a & b) | (c_in & (a ^ b)); return {c_out, s}; endfunction Bit#(1) a declaration says that a is one bit wide {c_out, s} represents bit concatenation How big is {c_out, s}? January 9, 2012 http: //csg. csail. mit. edu/SNU L 1 -10

Types Every expression and variable in a Bluespec program has a type; sometimes it is specified explicitly and sometimes it is deduced by the compiler A type is a grouping of values: n n n Integer: 1, 2, 3, … Bool: True, False Bit: 0, 1 A pair of Integers: Tuple 2#(Integer, Integer) A function fname from Integers to Integers: function Integer fname (Integer arg) Thus we say an expression has a type, belongs to a type The type of each expression is unique January 9, 2012 http: //csg. csail. mit. edu/SNU L 1 -11

Type declaration versus deduction User writes down types of some expressions in a program and the compiler deduces the types of the rest of expressions If the type deduction cannot be performed or the type declarations are inconsistent then the compiler complains function Bit#(2) fa(Bit#(1) a, Bit#(1) b, Bit#(1) c_in); Bit#(1) s = (a ^ b)^ c_in; Bit#(2) c_out = (a & b) | (c_in & (a ^ b)); return {c_out, s}; endfunction type error Type checking prevents lots of silly mistakes January 9, 2012 http: //csg. csail. mit. edu/SNU L 1 -12

2 -bit Ripple-Carry Adder function Bit#(3) add(Bit#(2) x, Bit#(2) y, Bit#(1) c 0); Bit#(2) s = 0; Bit#(3) c; c[0] = c 0; let cs 0 = fa(x[0], y[0], c[0]); c[1] = cs 0[1]; s[0] = cs 0[0]; let cs 1 = fa(x[1], y[1], c[1]); c[2] = cs 1[1]; s[1] = cs 1[0]; return {c[2], s}; x[0] y[0] x[1] y[1] endfunction c[0] fa s[0] January 9, 2012 http: //csg. csail. mit. edu/SNU c[1] fa c[2] s[1] L 1 -13

“let” syntax The “let” syntax: avoids having to write down types explicitly n n January 9, 2012 let cs 0 = fa(x[0], y[0], c[0]); Bits#(2) cs 0 = fa(x[0], y[0], c[0]); http: //csg. csail. mit. edu/SNU The same L 1 -14

Parameterized types: # A type declaration itself can be parameterized – the parameters are indicated by using the syntax ‘#’ n n January 9, 2012 For example Bit#(n) represents n bits and can be instantiated by specifying a value of n Bit#(1), Bit#(32), Bit#(8), … http: //csg. csail. mit. edu/SNU L 1 -15

An w-bit Ripple-Carry Adder function Bit#(w+1) add. N(Bit#(w) x, Bit#(w) y, Bit#(1) c 0); Bit#(w) s; Bit#(w+1) c; c[0] = c 0; for(Integer i=0; i<w; i=i+1) begin let cs = fa(x[i], y[i], c[i]); c[i+1] = cs[1]; s[i] = cs[0]; end Not quite correct return {c[w], s}; endfunction // concrete instances of add. N! function Bit#(33) add 32(Bit#(32) x, Bit#(32) y, Bit#(1) c 0) = add. N(x, y, c 0); function Bit#(4) add 3(Bit#(3) x, Bit#(3) y, Bit#(1) c 0) = add. N(x, y, c 0); January 9, 2012 http: //csg. csail. mit. edu/SNU L 1 -16
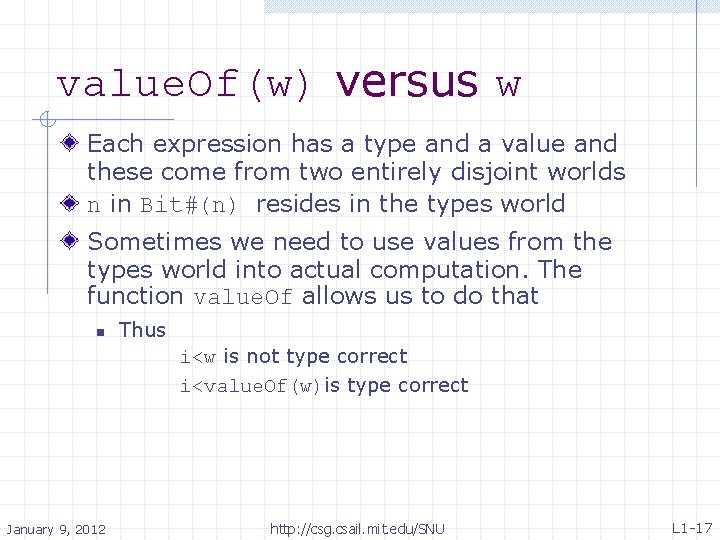
value. Of(w) versus w Each expression has a type and a value and these come from two entirely disjoint worlds n in Bit#(n) resides in the types world Sometimes we need to use values from the types world into actual computation. The function value. Of allows us to do that Thus i<w is not type correct i<value. Of(w)is type correct n January 9, 2012 http: //csg. csail. mit. edu/SNU L 1 -17

Tadd#(w, 1) versus w+1 Sometimes we need to perform operations in the types world that are very similar to the operations in the value world n Examples: Add, Mul, Log We define a few special operators in the types space for such operations n January 9, 2012 Examples: Tadd#(m, n), Tmul#(m, n), … http: //csg. csail. mit. edu/SNU L 1 -18

A w-bit Ripple-Carry Adder corrected function Bit#(Tadd#(w, 1)) add. N(Bit#(w) x, Bit#(w) y, Bit#(1) c 0); Bit#(w) s; Bit#(Tadd#(w, 1)) c; c[0] = c 0; let valw = value. Of(w); for(Integer i=0; i<valw; i=i+1) begin let cs = fa(x[i], y[i], c[i]); c[i+1] = cs[1]; s[i] = cs[0]; end return {c[valw], s}; endfunction January 9, 2012 http: //csg. csail. mit. edu/SNU L 1 -19

Integer versus Int#(32) In mathematics integers are unbounded but in computer systems integers always have a fixed size Bluespec allows us to express both types of integers, though unbounded integers are used only as a programming convenience for(Integer i=0; i<valw; i=i+1) begin let cs = fa(x[i], y[i], c[i]); c[i+1] = cs[1]; s[i] = cs[0]; end January 9, 2012 http: //csg. csail. mit. edu/SNU L 1 -20

Static Elaboration phase When Bluespec program are compiled, first type checking is done and then the compiler gets rid of many different constructs which have no direct hardware meaning, like Integers, loops for(Integer i=0; i<valw; i=i+1) begin let cs = fa(x[i], y[i], c[i]); c[i+1] = cs[1]; s[i] = cs[0]; end cs 0 = fa(x[0], y[0], c[0]); c[1]=cs 0[1]; s[0]=cs 0[0]; cs 1 = fa(x[1], y[1], c[1]); c[2]=cs 1[1]; s[1]=cs 1[0]; … csw = fa(x[w-1], y[w-1], c[w-1]); c[w] = csw[1]; s[w-1] = csw[0]; January 9, 2012 http: //csg. csail. mit. edu/SNU L 1 -21

Logical right shift by 2 abcd 0 0 00 ab Fixed size shift operation is cheap in hardware – just wire the circuit appropriately Rotate, sign-extended shifts – all are equally easy January 9, 2012 http: //csg. csail. mit. edu/SNU L 1 -22

Conditional operation: shift versus no-shift 0 0 s We need a Mux to select the appropriate wires: if s is one the Mux will select the wires on the left otherwise it would select wires on the right (s==0)? {a, b, c, d}: {0, 0, a, b}; January 9, 2012 http: //csg. csail. mit. edu/SNU L 1 -23
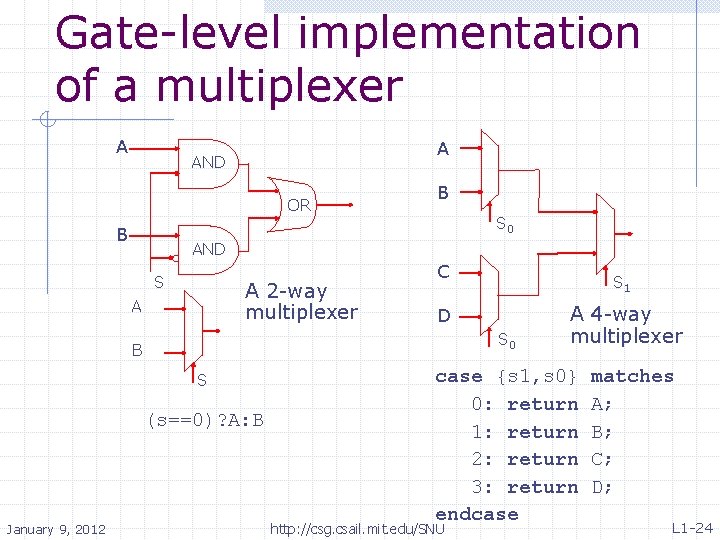
Gate-level implementation of a multiplexer A A AND OR B B S 0 AND S A 2 -way multiplexer A C D S 0 B S (s==0)? A: B January 9, 2012 S 1 A 4 -way multiplexer case {s 1, s 0} matches 0: return A; 1: return B; 2: return C; 3: return D; endcase http: //csg. csail. mit. edu/SNU L 1 -24
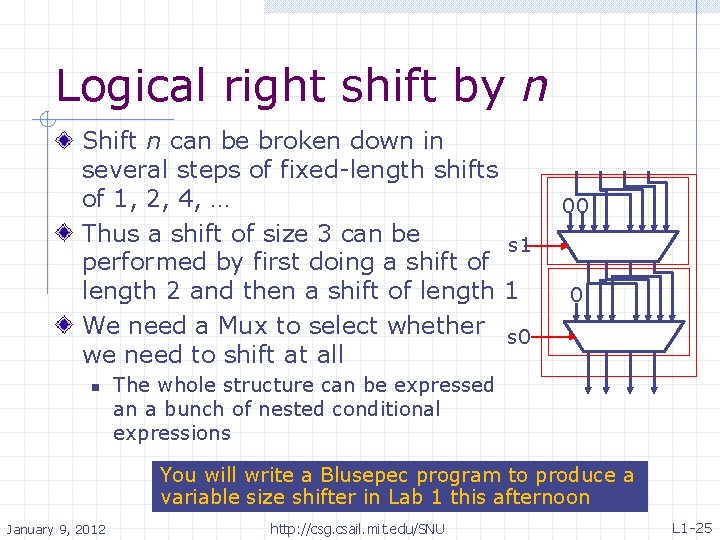
Logical right shift by n Shift n can be broken down in several steps of fixed-length shifts of 1, 2, 4, … Thus a shift of size 3 can be s 1 performed by first doing a shift of length 2 and then a shift of length 1 We need a Mux to select whether s 0 we need to shift at all n 00 0 The whole structure can be expressed an a bunch of nested conditional expressions You will write a Blusepec program to produce a variable size shifter in Lab 1 this afternoon January 9, 2012 http: //csg. csail. mit. edu/SNU L 1 -25

Combinational ALU function Bit#(width) comb. ALU(Bit#(width) a, Bit#(width) b, OP op); case op matches NOT: return ~a; Once we have AND: return a&b; implemented the OR: return a|b; primitive operations like add. N, >>, the ALU can SHL: return a<<b; be implemented simply SHR: return a>>b; by introducing a Mux ADD: return add. N(a, b); controlled by op to SUB: return a-b; select the appropriate MUL: return comb. Mul. N(a, b); circuit endcase slightly stylized code endfunction Other operations may be needed January 9, 2012 http: //csg. csail. mit. edu/SNU L 1 -26

Conditional operations Generate one-bit result which is used for branching n n n Eq (a, b) : (a == b); Neq(a, b) : (a != b); Le(a) : signed. LE(a, 0); Lt(a) : signed. LT(a, 0); Ge(a) : signed. GE(a, 0); Gt(a) : signed. GT(a, 0); Straightforward to implement; can be combined with the ALU with an extra bit of output January 9, 2012 http: //csg. csail. mit. edu/SNU L 1 -27
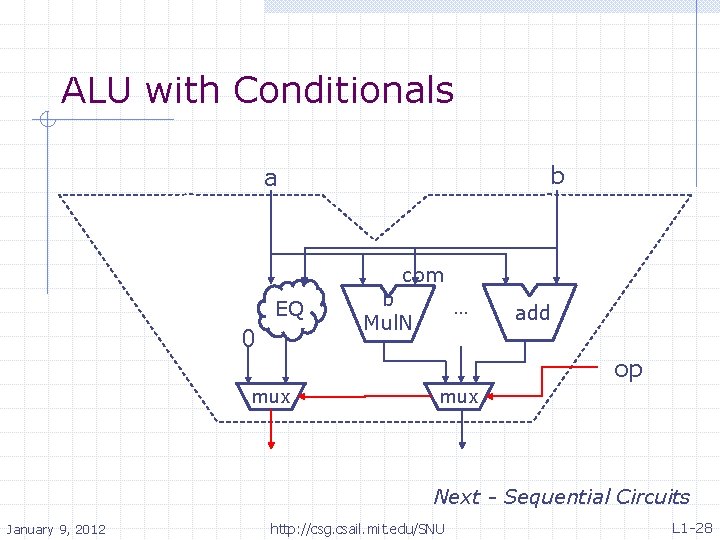
ALU with Conditionals b a com EQ 0 b Mul. N … add op mux Next - Sequential Circuits January 9, 2012 http: //csg. csail. mit. edu/SNU L 1 -28
- Slides: 28