Computer Animation Algorithms and Techniques Technical Background Rick

Computer Animation Algorithms and Techniques Technical Background Rick Parent Computer Animation

Spaces and Transformations Left-handed v. right handed Homogeneous coordinates: 4 x 4 transformation matrix (TM) Concatenating TMs Basic transformations (TMs) Display pipeline Rick Parent Computer Animation

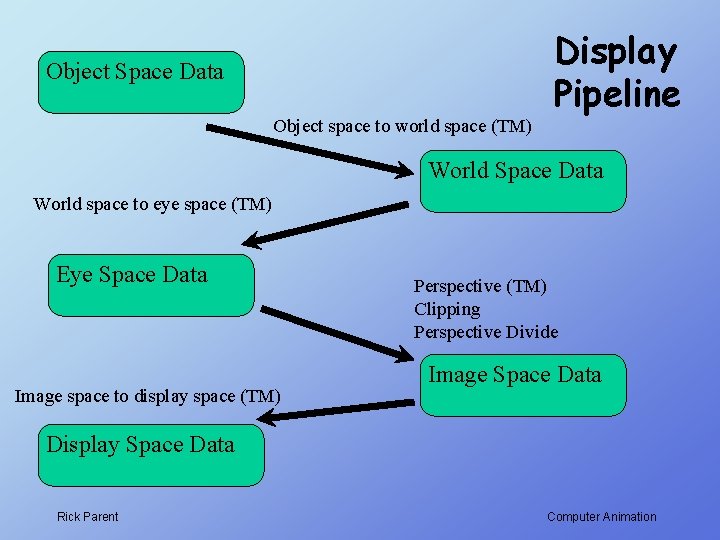
Object Space Data Object space to world space (TM) Display Pipeline World Space Data World space to eye space (TM) Eye Space Data Image space to display space (TM) Perspective (TM) Clipping Perspective Divide Image Space Data Display Space Data Rick Parent Computer Animation

Representing an orientation Example: fixed angles - rotate around global axes Y Orientation: X Z Rick Parent Computer Animation

Working with fixed angles and Rotation Matrices (RMs) Orthonormalizing a RM Y Extracing fixed angles from an orientation Z Extracing fixed angles from a RM Y X X Z Rick Parent Making a RM from fixed angles Making a RM from transformed unit coordinate system (TUCS) Computer Animation

Transformations in pipeline object -> world: often rigid transforms world -> eye: rigid transforms perspective matrix: uses 4 th component of homo. coords perspective divide image -> screen: 2 D map to screen coordinates Clipping: procedure that considers view frustum Rick Parent Computer Animation

Error considerations Accumulated round-off error - transform data: transform world data by delta RM update RM by delta RM; apply to object data update angle; form RM; apply to object data orthonormalization rotation matrix: orthogonal, unit-length columns iterate update by taking cross product of 2 vectors scale to unit length considerations of scale miles-to-inches can exeed single precision arithmetic Rick Parent Computer Animation

Orientation Representation Rotation matrix Fixed angles: rotate about global coordinate system Euler angles: rotate about local coordinate system Axis-angle: arbitrary axis and angle Quaternions: mathematically handy axis-angle 4 -tuple Exponential map: 3 -tuple version of quaternions Rick Parent Computer Animation

Transformation Matrix Rick Parent Computer Animation

Transformation Matrix Rick Parent Computer Animation

Rotation Matrices Rick Parent Computer Animation

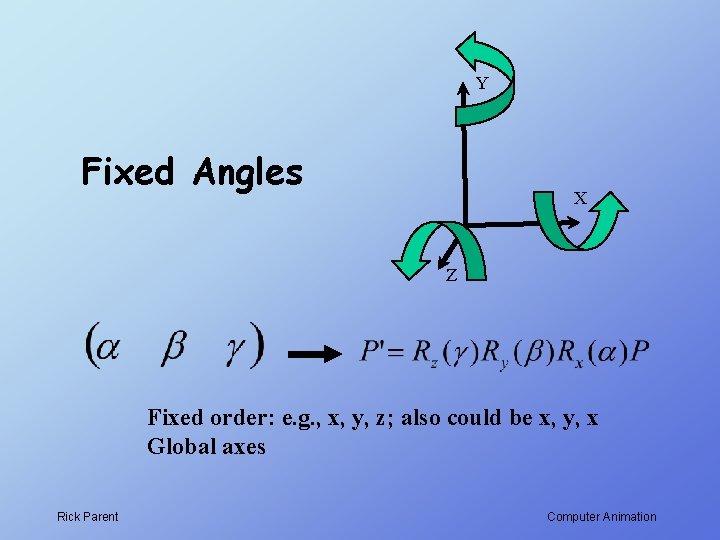
Y Fixed Angles X Z Fixed order: e. g. , x, y, z; also could be x, y, x Global axes Rick Parent Computer Animation

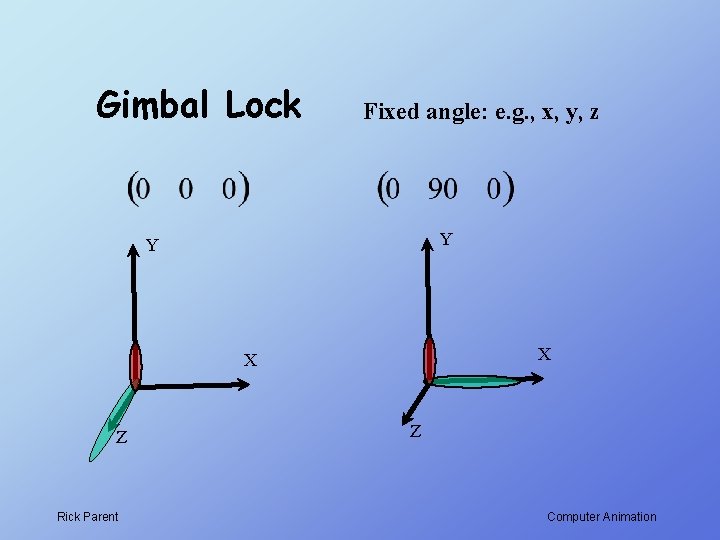
Gimbal Lock Fixed angle: e. g. , x, y, z Y Y X X Z Rick Parent Z Computer Animation

Gimbal Lock Fixed order of rotations: x, y, z What do these epsilon rotations do? Y X Z Rick Parent Computer Animation

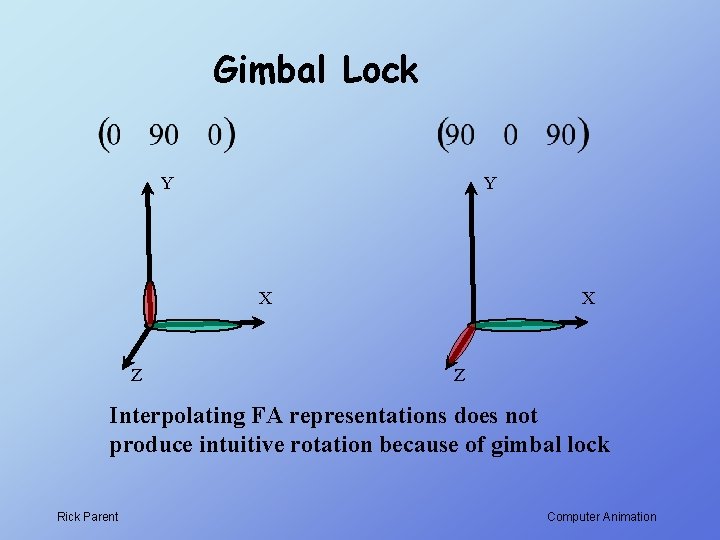
Gimbal Lock Y Y X X Z Z Interpolating FA representations does not produce intuitive rotation because of gimbal lock Rick Parent Computer Animation

Euler Angles Y X Prescribed order: e. g. , x, y, z or x, y, x Rotate around (rotated) local axes Z Note: fixed angles are same as Euler angles in reverse order and vice versa Rick Parent Computer Animation

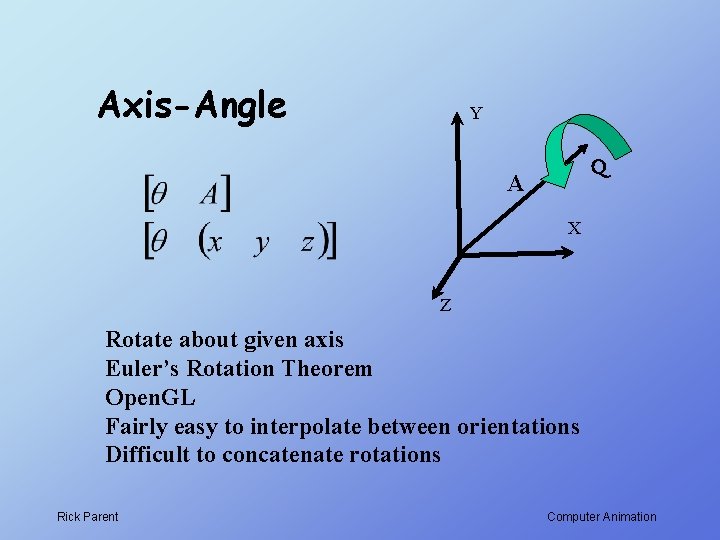
Axis-Angle Y Q A X Z Rotate about given axis Euler’s Rotation Theorem Open. GL Fairly easy to interpolate between orientations Difficult to concatenate rotations Rick Parent Computer Animation

Axis-angle to rotation matrix Y Q A X Z Rick Parent Concantenate the following: Rotate A around z to x-z plane Rotate A’ around y to x-axis Rotate theta around x Undo rotation around y-axis Undo rotation around z-axis Computer Animation

Axis-angle to rotation matrix Y A Q P’ X P Z Rick Parent Computer Animation

Quaternion Y Q A X Same as axis-angle, but different form Still rotate about given axis Mathematically convenient form Z Note: in this form v is a scaled version of the given axis of rotation, A Rick Parent Computer Animation

Quaternion Arithmetic Addition Multiplication Inner Product Length Rick Parent Computer Animation

Quaternion Arithmetic Inverse Unit quaternion Rick Parent Computer Animation

Quaternion Represention Vector Transform Rick Parent Computer Animation

Quaternion Geometric Operations Rick Parent Computer Animation

Unit Quaternion Conversions Axis-Angle Rick Parent Computer Animation

Quaternions Avoid gimbal lock Easy to rotate a point Easy to convert to a rotation matrix Easy to concatenate – quaternion multiply Easy to interpolate – interpolate 4 -tuples How about smoothly (in both space and time) interpolate? Rick Parent Computer Animation