Computer and Robot Vision I Chapter 8 The

Computer and Robot Vision I Chapter 8 The Facet Model Presented by: 蕭延儒 luis 862013@gmail. com 指導教授: 傅楸善 博士

8. 0 Outline l l l l 8. 1 Introduction 8. 2 Relative Maxima 8. 3 Sloped Facet Parameter and Error Estimation 8. 4 Facet-Based Peak Noise Removal 8. 5 Iterated Facet Model 8. 6 Gradient-Based Facet Edge Detection 8. 7 Bayesian Approach to Gradient Edge Detection 8. 8 Zero-Crossing Edge Detector 8. 9 Integrated Directional Derivative Gradient Operator 8. 10 Corner Detection 8. 11 Isotropic Derivative Magnitudes 8. 12 Ridges and Ravines on Digital Images 8. 13 Topographic Primal Sketch DC & CV Lab. CSIE NTU 1

Outline l l l l 8. 1 Introduction 8. 2 Relative Maxima 8. 3 Sloped Facet Parameter and Error Estimation 8. 4 Facet-Based Peak Noise Removal 8. 5 Iterated Facet Model 8. 6 Gradient-Based Facet Edge Detection 8. 7 Bayesian Approach to Gradient Edge Detection 8. 8 Zero-Crossing Edge Detector 8. 9 Integrated Directional Derivative Gradient Operator 8. 10 Corner Detection 8. 11 Isotropic Derivative Magnitudes 8. 12 Ridges and Ravines on Digital Images 8. 13 Topographic Primal Sketch DC & CV Lab. CSIE NTU 2

8. 1 Introduction l l The facet model principle states that the image can be thought of as an underlying continuum or piecewise continuous gray level intensity surface. observed digital image: noisy discretized sampling of distorted version of this surface DC & CV Lab. CSIE NTU 3

8. 1 Introduction l To actually carry out the processing with the observed digital image requires a model describes what the general form of the surface would be in the neighborhood of any pixel. https: //all 3 dp. com/what-is-stl-file-format-extension-3 d-printing/ DC & CV Lab. CSIE NTU 4

8. 1 Introduction l Example: Imagine an image (size=1*N) https: //all 3 dp. com/what-is-stl-file-format-extension-3 d-printing/ DC & CV Lab. CSIE NTU 5

8. 1 Introduction l Example: https: //all 3 dp. com/what-is-stl-file-format-extension-3 d-printing/ DC & CV Lab. CSIE NTU 6
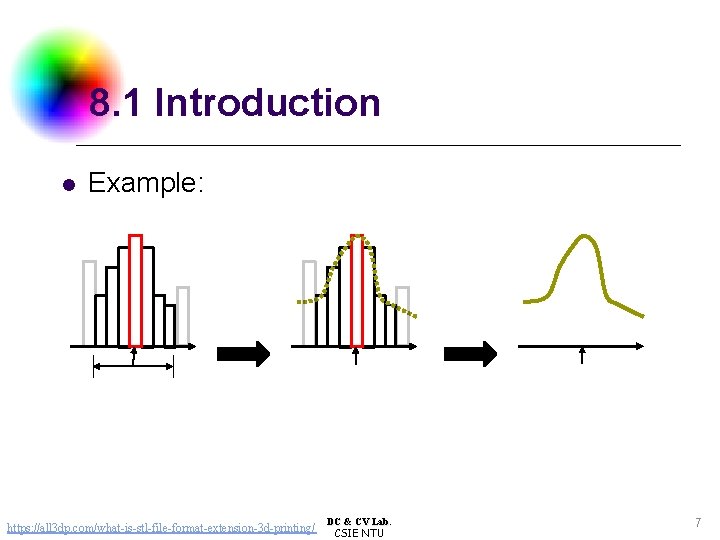
8. 1 Introduction l Example: https: //all 3 dp. com/what-is-stl-file-format-extension-3 d-printing/ DC & CV Lab. CSIE NTU 7
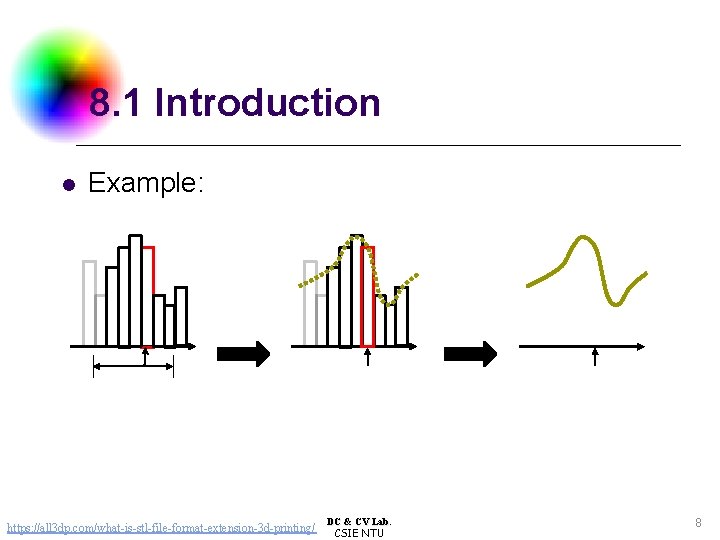
8. 1 Introduction l Example: https: //all 3 dp. com/what-is-stl-file-format-extension-3 d-printing/ DC & CV Lab. CSIE NTU 8

8. 1 Introduction l There are many kinds of facet model 1. piecewise constant (flat facet model) 2. piecewise linear (sloped facet model) 3. piecewise quadratic 4. piecewise cubic DC & CV Lab. CSIE NTU 9
8. 1 Introduction l Cubic surfaces https: //en. wikipedia. org/wiki/Cubic_surface DC & CV Lab. CSIE NTU 10

Outline l l l l 8. 1 Introduction 8. 2 Relative Maxima 8. 3 Sloped Facet Parameter and Error Estimation 8. 4 Facet-Based Peak Noise Removal 8. 5 Iterated Facet Model 8. 6 Gradient-Based Facet Edge Detection 8. 7 Bayesian Approach to Gradient Edge Detection 8. 8 Zero-Crossing Edge Detector 8. 9 Integrated Directional Derivative Gradient Operator 8. 10 Corner Detection 8. 11 Isotropic Derivative Magnitudes 8. 12 Ridges and Ravines on Digital Images 8. 13 Topographic Primal Sketch DC & CV Lab. CSIE NTU 11

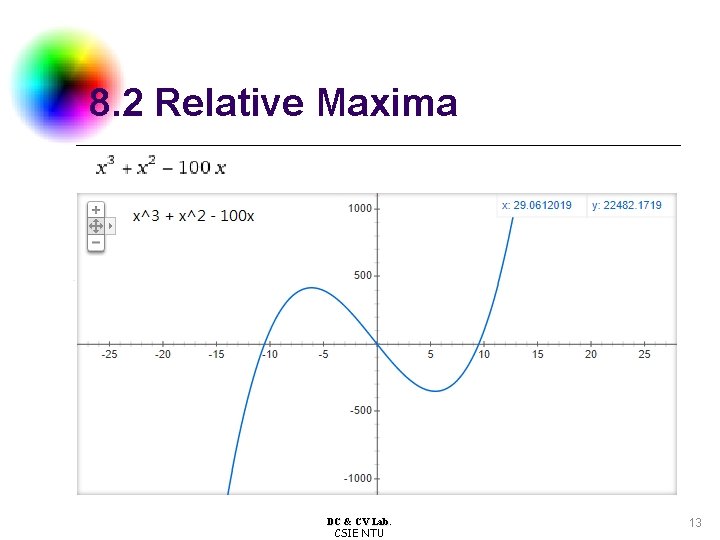
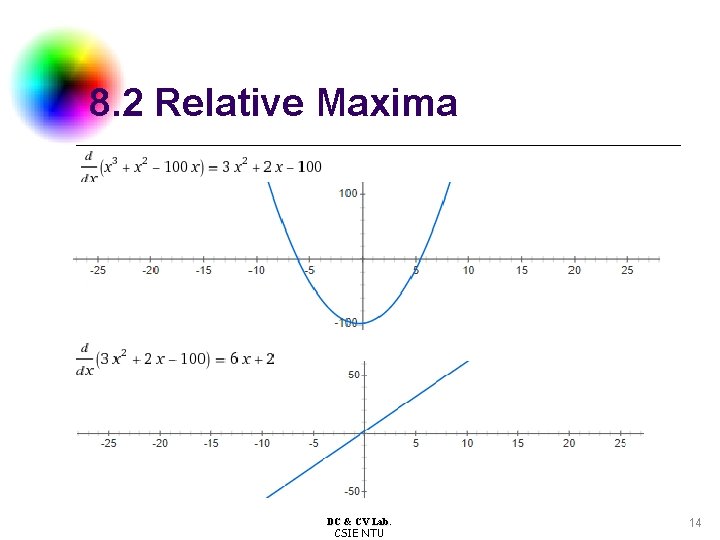
8. 2 Relative Maxima l a simple labeling application l l Detect and locate all relative maxima: l l first derivative zero second derivative negative DC & CV Lab. CSIE NTU 12
8. 2 Relative Maxima DC & CV Lab. CSIE NTU 13
8. 2 Relative Maxima DC & CV Lab. CSIE NTU 14

8. 2 Relative Maxima l DC & CV Lab. CSIE NTU 15

8. 2 Relative Maxima l DC & CV Lab. CSIE NTU 16

8. 2 Relative Maxima l (-1, 3), (0, 4), (1, 5) DC & CV Lab. CSIE NTU 17

8. 2 Relative Maxima l (-1, 3), (0, 4), (1, 5) (-1, 4), (0, 5), (1, 2) DC & CV Lab. CSIE NTU 18

8. 2 Relative Maxima (-1, 3), (0, 4), (1, 5) (-1, 5), (0, 2), (1, 7) (-1, 4), (0, 5), (1, 2) (-1, 2), (0, 7), (1, 8) DC & CV Lab. CSIE NTU 19
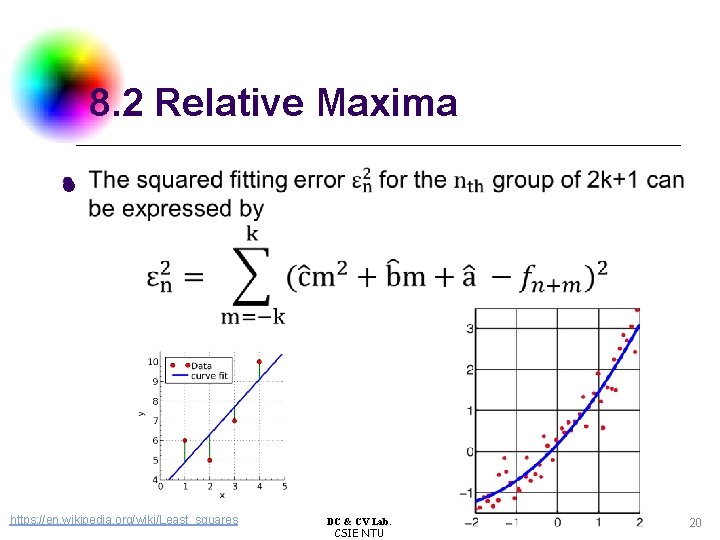
8. 2 Relative Maxima l https: //en. wikipedia. org/wiki/Least_squares DC & CV Lab. CSIE NTU 20

8. 2 Relative Maxima l https: //en. wikipedia. org/wiki/Least_squares DC & CV Lab. CSIE NTU 21

8. 2 Relative Maxima l DC & CV Lab. CSIE NTU 22
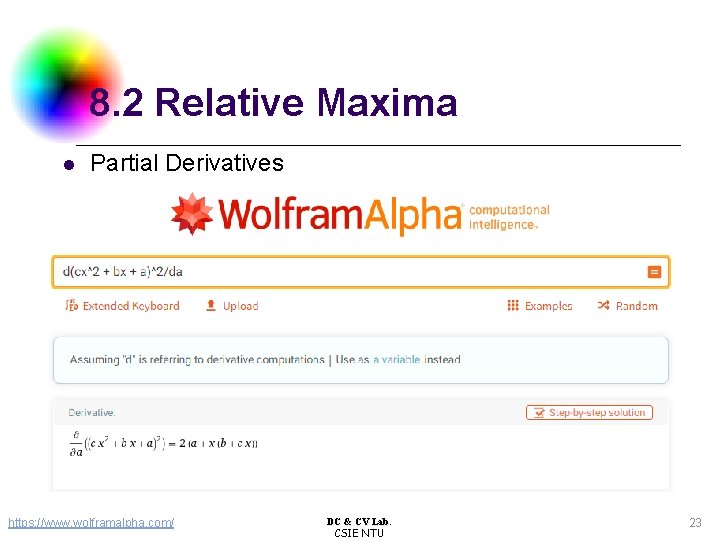
8. 2 Relative Maxima l Partial Derivatives https: //www. wolframalpha. com/ DC & CV Lab. CSIE NTU 23

8. 2 Relative Maxima l Assume k = 1, setting these partial derivatives to zero and simplifying yields the matrix equation from DC & CV Lab. CSIE NTU 24

8. 2 Relative Maxima l DC & CV Lab. CSIE NTU 25

8. 2 Relative Maxima DC & CV Lab. CSIE NTU 26
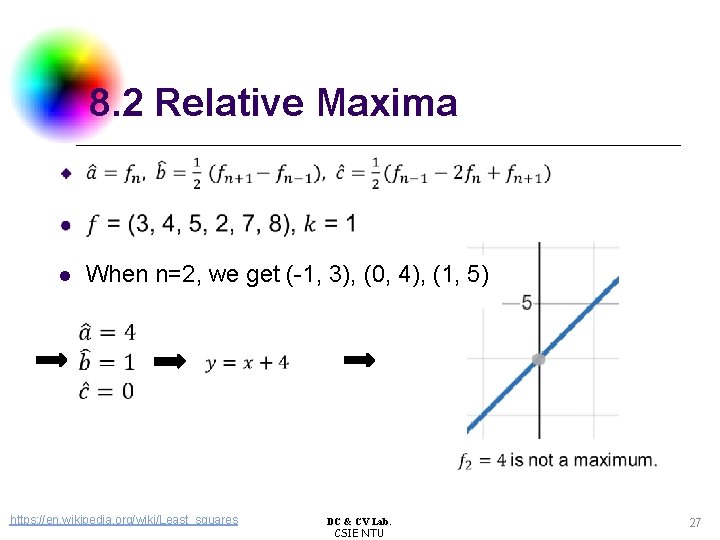
8. 2 Relative Maxima When n=2, we get (-1, 3), (0, 4), (1, 5) l https: //en. wikipedia. org/wiki/Least_squares DC & CV Lab. CSIE NTU 27
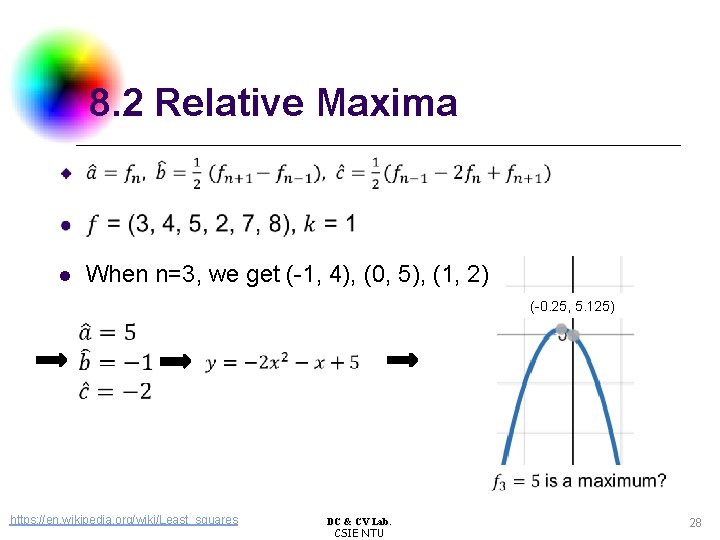
8. 2 Relative Maxima When n=3, we get (-1, 4), (0, 5), (1, 2) l (-0. 25, 5. 125) https: //en. wikipedia. org/wiki/Least_squares DC & CV Lab. CSIE NTU 28

8. 2 Relative Maxima l DC & CV Lab. CSIE NTU 29
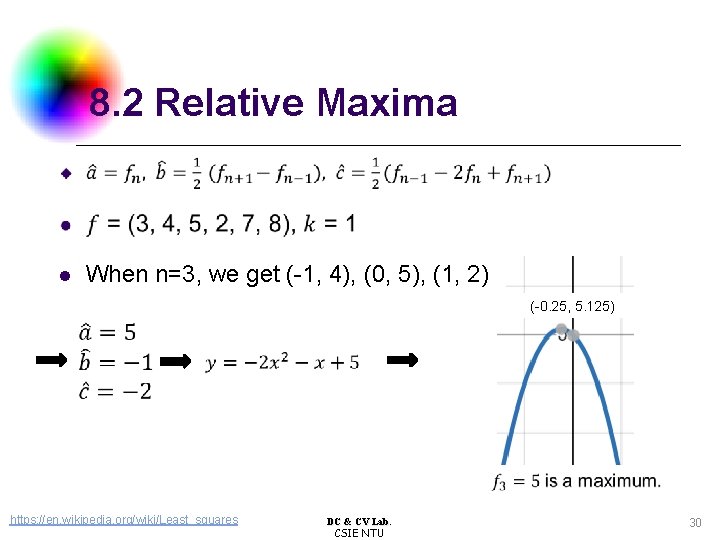
8. 2 Relative Maxima When n=3, we get (-1, 4), (0, 5), (1, 2) l (-0. 25, 5. 125) https: //en. wikipedia. org/wiki/Least_squares DC & CV Lab. CSIE NTU 30
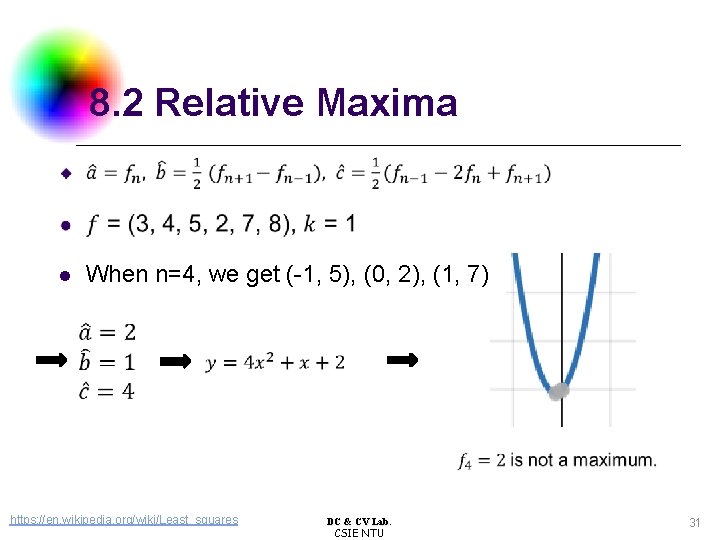
8. 2 Relative Maxima When n=4, we get (-1, 5), (0, 2), (1, 7) l https: //en. wikipedia. org/wiki/Least_squares DC & CV Lab. CSIE NTU 31
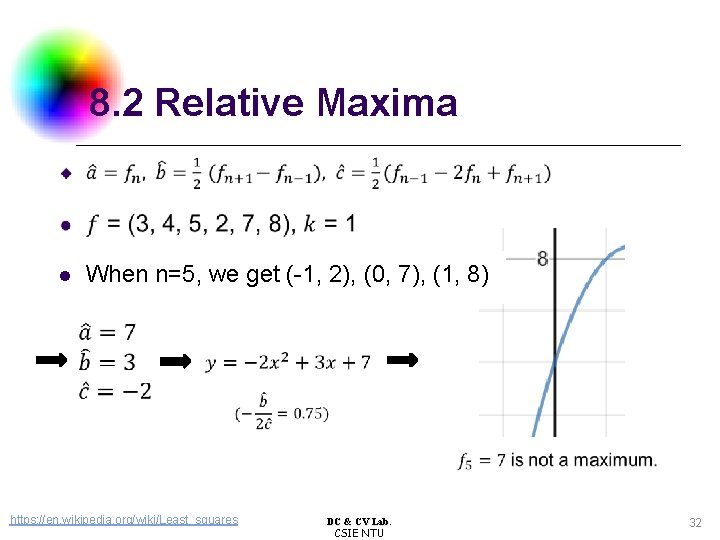
8. 2 Relative Maxima When n=5, we get (-1, 2), (0, 7), (1, 8) l https: //en. wikipedia. org/wiki/Least_squares DC & CV Lab. CSIE NTU 32

Outline l l l l 8. 1 Introduction 8. 2 Relative Maxima 8. 3 Sloped Facet Parameter and Error Estimation 8. 4 Facet-Based Peak Noise Removal 8. 5 Iterated Facet Model 8. 6 Gradient-Based Facet Edge Detection 8. 7 Bayesian Approach to Gradient Edge Detection 8. 8 Zero-Crossing Edge Detector 8. 9 Integrated Directional Derivative Gradient Operator 8. 10 Corner Detection 8. 11 Isotropic Derivative Magnitudes 8. 12 Ridges and Ravines on Digital Images 8. 13 Topographic Primal Sketch DC & CV Lab. CSIE NTU 33

8. 3 Sloped Facet Parameter and Error Estimation l Similar to 8. 2, we employ a least-squares procedure both to estimate the parameters of the sloped facet model. l Given two-dimensional rectangular neighborhood, the row index set is R and the column index set is C DC & CV Lab. CSIE NTU 34

8. 3 Sloped Facet Parameter and Error Estimation l observed truth noise DC & CV Lab. CSIE NTU 35

8. 3 Sloped Facet Parameter and Error Estimation l estimated DC & CV Lab. CSIE NTU observed 36

8. 3 Sloped Facet Parameter and Error Estimation l l We choose our coordinate Rx. C so that the center of the neighborhood Rx. C has coordinates (0, 0) The symmetry in the chosen coordinate system leads to l and Hence DC & CV Lab. CSIE NTU 37

8. 3 Sloped Facet Parameter and Error Estimation DC & CV Lab. CSIE NTU 38

8. 3 Sloped Facet Parameter and Error Estimation DC & CV Lab. CSIE NTU 39

8. 3 Sloped Facet Parameter and Error Estimation 0 0 DC & CV Lab. CSIE NTU 40

8. 3 Sloped Facet Parameter and Error Estimation 0 0 DC & CV Lab. CSIE NTU 41

8. 3 Sloped Facet Parameter and Error Estimation 0 0 DC & CV Lab. CSIE NTU 42

8. 3 Sloped Facet Parameter and Error Estimation 0 0 DC & CV Lab. CSIE NTU 43

8. 3 Sloped Facet Parameter and Error Estimation l DC & CV Lab. CSIE NTU 44

8. 3 Sloped Facet Parameter and Error Estimation l Example: consider the following 3*3 region 3 5 9 4 7 7 0 3 7 DC & CV Lab. CSIE NTU 45

8. 3 Sloped Facet Parameter and Error Estimation l Example: 3 5 9 4 7 7 0 3 7 DC & CV Lab. CSIE NTU 46

8. 3 Sloped Facet Parameter and Error Estimation l Example: 3 5 9 4 7 7 0 3 7 DC & CV Lab. CSIE NTU 47

8. 3 Sloped Facet Parameter and Error Estimation l Example: 3 5 9 4 7 7 0 3 7 DC & CV Lab. CSIE NTU 48

8. 3 Sloped Facet Parameter and Error Estimation Example: l r c -1 0 1 estimated DC & CV Lab. CSIE NTU 49

8. 3 Sloped Facet Parameter and Error Estimation l Example: 3. 5 estimated DC & CV Lab. CSIE NTU 50

8. 3 Sloped Facet Parameter and Error Estimation l Example: 3. 5 6. 17 estimated DC & CV Lab. CSIE NTU 51

8. 3 Sloped Facet Parameter and Error Estimation l Example: 3. 5 6. 17 8. 84 estimated DC & CV Lab. CSIE NTU 52

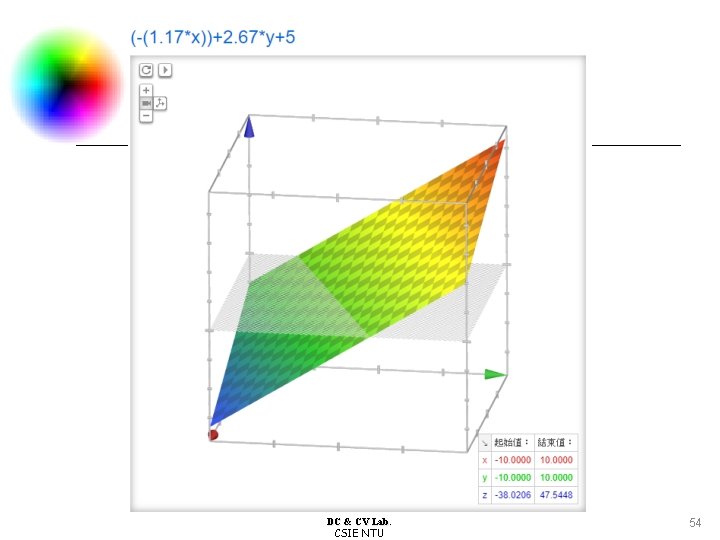
8. 3 Sloped Facet Parameter and Error Estimation l Example: 3. 5 6. 17 8. 84 2. 33 5 7. 67 1. 17 3. 83 6. 5 estimated DC & CV Lab. CSIE NTU 53
DC & CV Lab. CSIE NTU 54

8. 3 Sloped Facet Parameter and Error Estimation l Example: Calculate the error: 3. 5 6. 17 8. 84 2. 33 5 7. 67 1. 17 3. 83 6. 5 estimated 3 5 9 - = 0. 5 1. 17 -0. 17 4 7 7 -1. 67 -2 0. 67 0 3 7 1. 17 0. 83 -0. 5 observed DC & CV Lab. CSIE NTU error 55

8. 3 Sloped Facet Parameter and Error Estimation Example: l r c -1 0 1 -1 0. 5 1. 17 -0. 17 0 -1. 67 -2 0. 67 1 1. 17 0. 83 -0. 5 DC & CV Lab. CSIE NTU 56

8. 3 Sloped Facet Parameter and Error Estimation l DC & CV Lab. CSIE NTU 57

8. 3 Sloped Facet Parameter and Error Estimation l 3 5 9 4 7 7 0 3 7 observed DC & CV Lab. CSIE NTU 58

Outline l l l l 8. 1 Introduction 8. 2 Relative Maxima 8. 3 Sloped Facet Parameter and Error Estimation 8. 4 Facet-Based Peak Noise Removal 8. 5 Iterated Facet Model 8. 6 Gradient-Based Facet Edge Detection 8. 7 Bayesian Approach to Gradient Edge Detection 8. 8 Zero-Crossing Edge Detector 8. 9 Integrated Directional Derivative Gradient Operator 8. 10 Corner Detection 8. 11 Isotropic Derivative Magnitudes 8. 12 Ridges and Ravines on Digital Images 8. 13 Topographic Primal Sketch DC & CV Lab. CSIE NTU 59

8. 4 Facet-Based Peak Noise Removal l Peak noise pixel: a pixel whose gray level intensity significantly differs from neighborhood pixels. l It is difficult to judge that the center pixel in part (b) is peak noise, whereas it is easier in part (a) DC & CV Lab. CSIE NTU

8. 4 Facet-Based Peak Noise Removal l Let N be a set of neighborhood pixels that does not contain the center pixel (-1, -1) (-1, 0) (-1, 1) (0, -1) (0, 0) (0, 1) (1, -1) (1, 0) (1, 1) observed truth noise DC & CV Lab. CSIE NTU 61

8. 4 Facet-Based Peak Noise Removal l DC & CV Lab. CSIE NTU 62

8. 4 Facet-Based Peak Noise Removal l DC & CV Lab. CSIE NTU 63
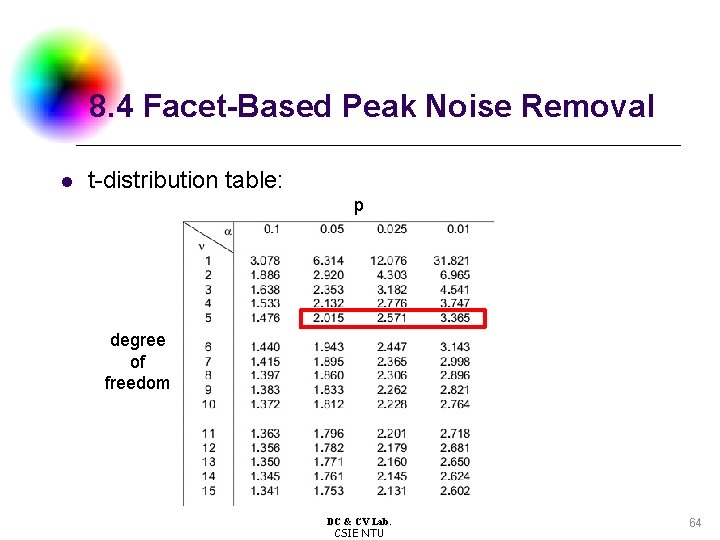
8. 4 Facet-Based Peak Noise Removal l t-distribution table: p degree of freedom DC & CV Lab. CSIE NTU 64

8. 4 Facet-Based Peak Noise Removal l DC & CV Lab. CSIE NTU 65

8. 4 Facet-Based Peak Noise Removal l Example: consider the following 3*3 region 3 5 3 4 9 3 0 3 3 DC & CV Lab. CSIE NTU 66

8. 4 Facet-Based Peak Noise Removal l Example: 3 5 3 4 9 3 0 3 3 DC & CV Lab. CSIE NTU 67
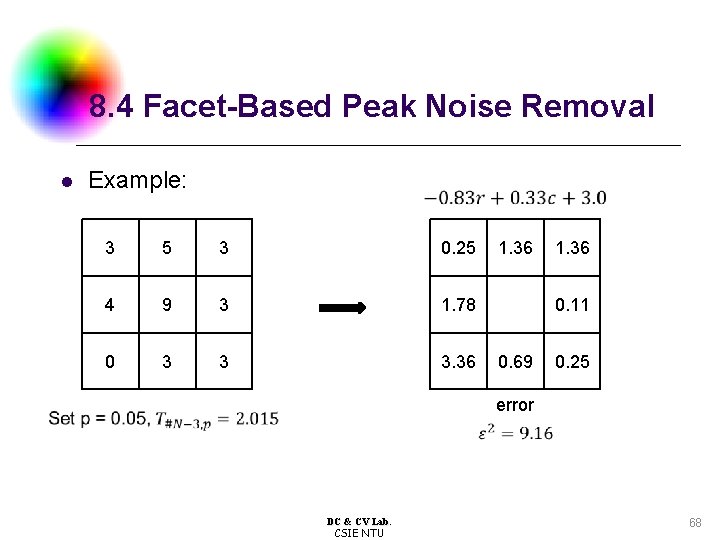
8. 4 Facet-Based Peak Noise Removal l Example: 3 5 3 0. 25 4 9 3 1. 78 0 3 3 3. 36 DC & CV Lab. CSIE NTU 1. 36 0. 11 0. 69 0. 25 error 68

8. 4 Facet-Based Peak Noise Removal l Example: 3 5 3 4 9 3 0 3 3 DC & CV Lab. CSIE NTU 69

8. 4 Facet-Based Peak Noise Removal l Example: 3 5 3 4 9 3 0 3 3 DC & CV Lab. CSIE NTU 70

8. 4 Facet-Based Peak Noise Removal l Example: 3 5 3 4 9. 5 3 0 3 3 DC & CV Lab. CSIE NTU 71

8. 4 Facet-Based Peak Noise Removal l Example: 3 5 3 4 3 3 0 3 3 DC & CV Lab. CSIE NTU 72

Outline l l l l 8. 1 Introduction 8. 2 Relative Maxima 8. 3 Sloped Facet Parameter and Error Estimation 8. 4 Facet-Based Peak Noise Removal 8. 5 Iterated Facet Model 8. 6 Gradient-Based Facet Edge Detection 8. 7 Bayesian Approach to Gradient Edge Detection 8. 8 Zero-Crossing Edge Detector 8. 9 Integrated Directional Derivative Gradient Operator 8. 10 Corner Detection 8. 11 Isotropic Derivative Magnitudes 8. 12 Ridges and Ravines on Digital Images 8. 13 Topographic Primal Sketch DC & CV Lab. CSIE NTU 73

8. 5 Iterated Facet Model The iterated model for ideal image l l The spatial of the image can be partitioned into connected regions called facets. Each of which satisfies certain gray level and shape constraints. DC & CV Lab. CSIE NTU 74

8. 5 Iterated Facet Model The iterated model for ideal image https: //www. pinterest. com/pin/296674694187240243/ DC & CV Lab. CSIE NTU 75

8. 5 Iterated Facet Model l DC & CV Lab. CSIE NTU

8. 5 Iterated Facet Model l Example: DC & CV Lab. CSIE NTU

8. 5 Iterated Facet Model l Example: DC & CV Lab. CSIE NTU

8. 5 Iterated Facet Model l Example: DC & CV Lab. CSIE NTU

8. 5 Iterated Facet Model l Example: DC & CV Lab. CSIE NTU

8. 5 Iterated Facet Model l Example: DC & CV Lab. CSIE NTU

Outline l l l l 8. 1 Introduction 8. 2 Relative Maxima 8. 3 Sloped Facet Parameter and Error Estimation 8. 4 Facet-Based Peak Noise Removal 8. 5 Iterated Facet Model 8. 6 Gradient-Based Facet Edge Detection 8. 7 Bayesian Approach to Gradient Edge Detection 8. 8 Zero-Crossing Edge Detector 8. 9 Integrated Directional Derivative Gradient Operator 8. 10 Corner Detection 8. 11 Isotropic Derivative 8. 12 Ridges and Ravines on Digital Images 8. 13 Topographic Primal Sketch DC & CV Lab. CSIE NTU 82
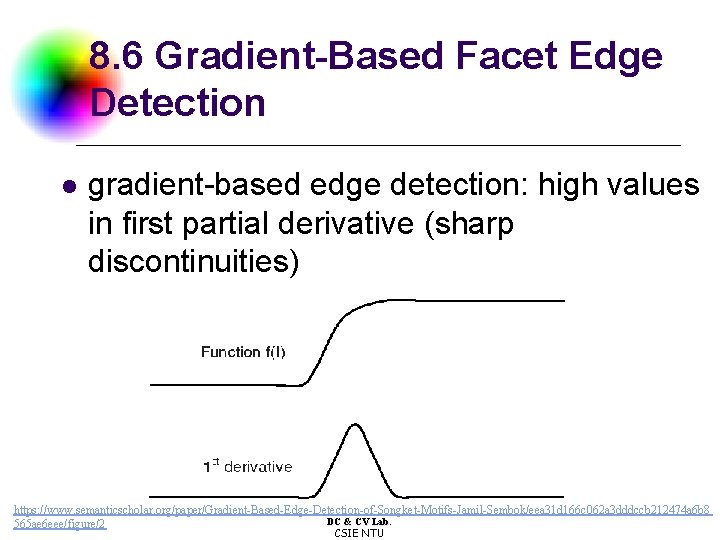
8. 6 Gradient-Based Facet Edge Detection l gradient-based edge detection: high values in first partial derivative (sharp discontinuities) https: //www. semanticscholar. org/paper/Gradient-Based-Edge-Detection-of-Songket-Motifs-Jamil-Sembok/eea 31 d 166 c 062 a 3 dddccb 212474 a 6 b 8 DC & CV Lab. 565 ae 6 eee/figure/2 CSIE NTU

8. 6 Gradient-Based Facet Edge Detection l DC & CV Lab. CSIE NTU 84

8. 6 Gradient-Based Facet Edge Detection l For example: 3. 5 6. 17 8. 84 2. 33 5 7. 67 1. 17 3. 83 6. 5 DC & CV Lab. CSIE NTU 85

8. 6 Gradient-Based Facet Edge Detection l DC & CV Lab. CSIE NTU 86

8. 6 Gradient-Based Facet Edge Detection l DC & CV Lab. CSIE NTU 87

8. 6 Gradient-Based Facet Edge Detection l DC & CV Lab. CSIE NTU 88
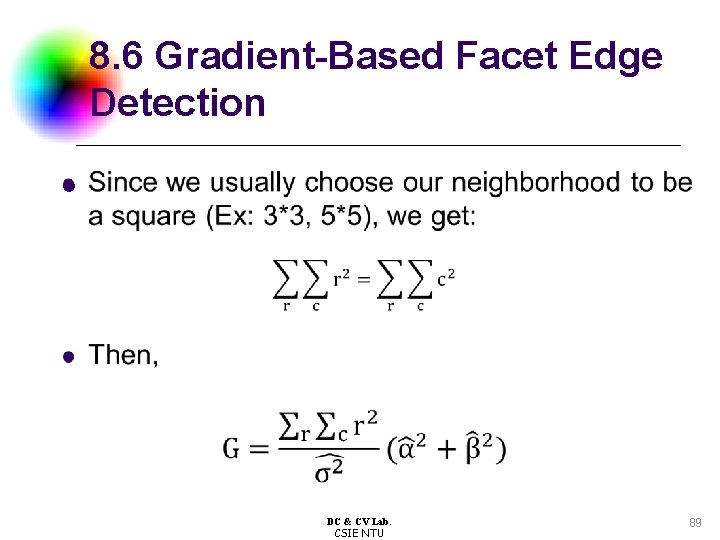
8. 6 Gradient-Based Facet Edge Detection l DC & CV Lab. CSIE NTU 89

8. 6 Gradient-Based Facet Edge Detection l DC & CV Lab. CSIE NTU 90

8. 6 Gradient-Based Facet Edge Detection DC & CV Lab. CSIE NTU 91
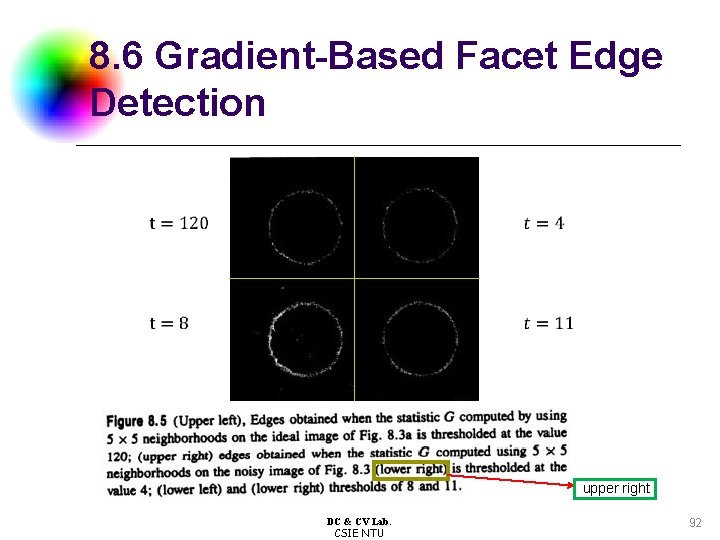
8. 6 Gradient-Based Facet Edge Detection upper right DC & CV Lab. CSIE NTU 92

8. 6 Gradient-Based Facet Edge Detection l Example: lena. bmp DC & CV Lab. CSIE NTU 93

8. 6 Gradient-Based Facet Edge Detection l Example: Set neighborhood size to 3*3 Original Slope image DC & CV Lab. CSIE NTU 94

8. 6 Gradient-Based Facet Edge Detection l Example: Set neighborhood size to 3*3, threshold to 10, 60, 120, respectively. DC & CV Lab. CSIE NTU 95

8. 6 Gradient-Based Facet Edge Detection l Example: Set neighborhood size to 5*5 Original Slope image DC & CV Lab. CSIE NTU 96

8. 6 Gradient-Based Facet Edge Detection l Example: Set neighborhood size to 5*5, threshold to 10, 60, 120, respectively. DC & CV Lab. CSIE NTU 97

8. 6 Gradient-Based Facet Edge Detection l Example: Set neighborhood size to 3*3, threshold to 10, 60, 120, respectively. DC & CV Lab. CSIE NTU 98

Outline l l l l 8. 1 Introduction 8. 2 Relative Maxima 8. 3 Sloped Facet Parameter and Error Estimation 8. 4 Facet-Based Peak Noise Removal 8. 5 Iterated Facet Model 8. 6 Gradient-Based Facet Edge Detection 8. 7 Bayesian Approach to Gradient Edge Detection 8. 8 Zero-Crossing Edge Detector 8. 9 Integrated Directional Derivative Gradient Operator 8. 10 Corner Detection 8. 11 Isotropic Derivative Magnitudes 8. 12 Ridges and Ravines on Digital Images 8. 13 Topographic Primal Sketch DC & CV Lab. CSIE NTU 99

8. 7 Bayesian Approach to Gradient Edge Detection l DC & CV Lab. CSIE NTU

8. 7 Bayesian Approach to Gradient Edge Detection Hence, a decision for edge is made whenever DC & CV Lab. CSIE NTU 101

8. 7 Bayesian Approach to Gradient Edge Detection l DC & CV Lab. CSIE NTU 102

8. 7 Bayesian Approach to Gradient Edge Detection l DC & CV Lab. CSIE NTU 103

8. 7 Bayesian Approach to Gradient Edge Detection l DC & CV Lab. CSIE NTU 104

Outline l l l l 8. 1 Introduction 8. 2 Relative Maxima 8. 3 Sloped Facet Parameter and Error Estimation 8. 4 Facet-Based Peak Noise Removal 8. 5 Iterated Facet Model 8. 6 Gradient-Based Facet Edge Detection 8. 7 Bayesian Approach to Gradient Edge Detection 8. 8 Zero-Crossing Edge Detector 8. 9 Integrated Directional Derivative Gradient Operator 8. 10 Corner Detection 8. 11 Isotropic Derivative Magnitudes 8. 12 Ridges and Ravines on Digital Images 8. 13 Topographic Primal Sketch DC & CV Lab. CSIE NTU 105

8. 8 Zero-Crossing Edge Detector l compare l l l gradient edge detector: looks for high values of first derivatives zero-crossing edge detector: looks for relative maxima in first derivative In what follows we assume that in each neighborhood of the images, the underlying graylevel intensity function f takes the form DC & CV Lab. CSIE NTU
8. 8 Zero-Crossing Edge Detector http: //140. 117. 156. 238/course/CSSV/2011/%E 7%9 B%A 3%E 6%8 E%A 7%E 8%A 6%96%E 8%A 8%8 A_ch 3. pdf DC & CV Lab. CSIE NTU

8. 8. 1 Discrete Orthogonal Polynomials l l The underlying functions from which the directional derivative are computed are easy to represent as linear combinations of the polynomials in any polynomial basis set. 刪掉 basis set: l The discrete orthogonal polynomials DC & CV Lab. CSIE NTU 108

8. 8. 1 Discrete Orthogonal Polynomials l Index Set Discrete Orthogonal Polynomial Set DC & CV Lab. CSIE NTU

8. 8. 1 Discrete Orthogonal Polynomials (cont’) l DC & CV Lab. CSIE NTU

8. 8. 1 Discrete Orthogonal Polynomials (cont’) l DC & CV Lab. CSIE NTU

8. 8. 1 Discrete Orthogonal Polynomials (cont’) l DC & CV Lab. CSIE NTU

8. 8. 1 Discrete Orthogonal Polynomials (cont’) l DC & CV Lab. CSIE NTU

8. 8. 1 Discrete Orthogonal Polynomials (cont’) DC & CV Lab. CSIE NTU

8. 8. 1 Discrete Orthogonal Polynomials (cont’) DC & CV Lab. CSIE NTU

8. 8. 1 Discrete Orthogonal Polynomials (cont’) Ex. l Index Set Discrete Orthogonal Polynomial Set DC & CV Lab. CSIE NTU

8. 8. 2 Two-Dimensional Discrete Orthogonal Polynomials l 2 -D discrete orthogonal polynomials creatable from tensor products of 1 D from above equations DC & CV Lab. CSIE NTU

8. 8. 2 Two-Dimensional Discrete Orthogonal Polynomials l l DC & CV Lab. CSIE NTU

8. 8. 2 Two-Dimensional Discrete Orthogonal Polynomials l 2 -D discrete orthogonal polynomials creatable from tensor products of 1 D from above equations DC & CV Lab. CSIE NTU

8. 8. 3 Equal-Weighted Least. Squares Fitting Problem l DC & CV Lab. CSIE NTU 120

8. 8. 3 Equal-Weighted Least. Squares Fitting Problem l Proof DC & CV Lab. CSIE NTU 121

8. 8. 3 Equal-Weighted Least. Squares Fitting Problem DC & CV Lab. CSIE NTU

8. 8. 3 Equal-Weighted Least. Squares Fitting Problem (cont’) DC & CV Lab. CSIE NTU
Break time DC & CV Lab. CSIE NTU 124

8. 8. 4 Directional Derivative Edge Finder l l l We define the directional derivative edge finder as the operator that places an edge in all pixels having a negatively sloped zero crossing of the second directional derivative taken in the direction of the gradient r: row c: column ρ: radius in polar coordinate α: angle in polar coordinate, clockwise from column axis DC & CV Lab. CSIE NTU

8. 8. 4 Directional Derivative Edge Finder (cont’) l DC & CV Lab. CSIE NTU

8. 8. 4 Directional Derivative Edge Finder (cont’) DC & CV Lab. CSIE NTU 127

8. 8. 4 Directional Derivative Edge Finder (cont’) l DC & CV Lab. CSIE NTU

8. 8. 4 Directional Derivative Edge Finder (cont’) l DC & CV Lab. CSIE NTU 129

8. 8. 4 Directional Derivative Edge Finder (cont’) 4. 6 Directional Derivatives and the Gradient DC & CV Lab. CSIE NTU 130
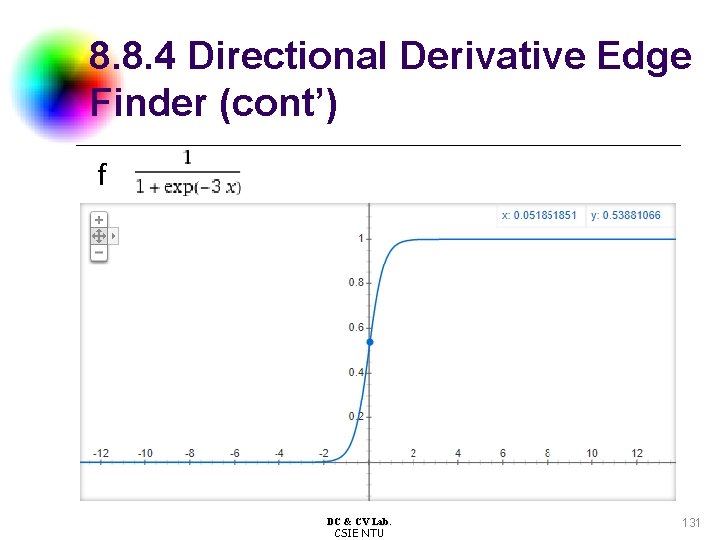
8. 8. 4 Directional Derivative Edge Finder (cont’) f DC & CV Lab. CSIE NTU 131
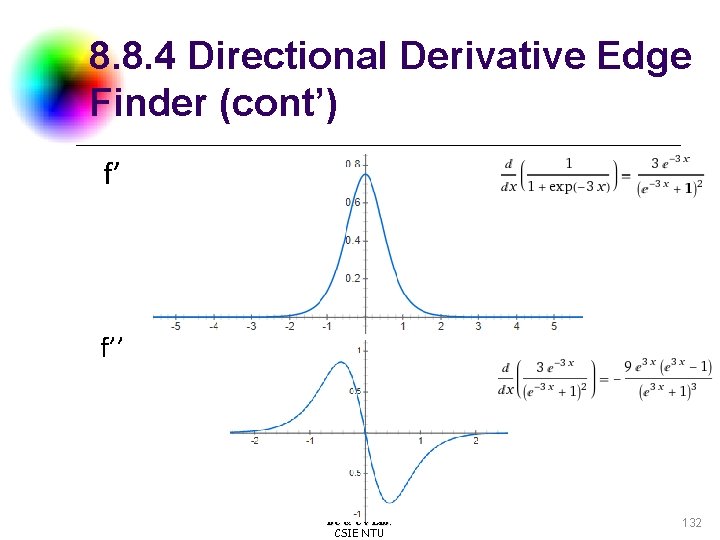
8. 8. 4 Directional Derivative Edge Finder (cont’) f’ f’’ DC & CV Lab. CSIE NTU 132
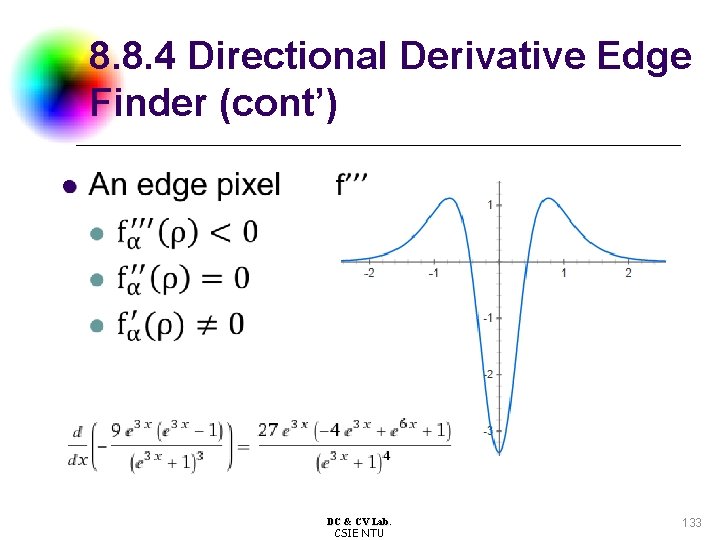
8. 8. 4 Directional Derivative Edge Finder (cont’) l DC & CV Lab. CSIE NTU 133

Outline l l l l 8. 1 Introduction 8. 2 Relative Maxima 8. 3 Sloped Facet Parameter and Error Estimation 8. 4 Facet-Based Peak Noise Removal 8. 5 Iterated Facet Model 8. 6 Gradient-Based Facet Edge Detection 8. 7 Bayesian Approach to Gradient Edge Detection 8. 8 Zero-Crossing Edge Detector 8. 9 Integrated Directional Derivative Gradient Operator 8. 10 Corner Detection 8. 11 Isotropic Derivative Magnitudes 8. 12 Ridges and Ravines on Digital Images 8. 13 Topographic Primal Sketch DC & CV Lab. CSIE NTU 134

8. 9 Integrated Directional Derivative Gradient Operator l integrated directional derivative gradient operator l l an operator that measures the integrated directional derivative strength as the integral of first directional derivative taken over a square area more accurate step edge direction DC & CV Lab. CSIE NTU Journals

Outline l l l l 8. 1 Introduction 8. 2 Relative Maxima 8. 3 Sloped Facet Parameter and Error Estimation 8. 4 Facet-Based Peak Noise Removal 8. 5 Iterated Facet Model 8. 6 Gradient-Based Facet Edge Detection 8. 7 Bayesian Approach to Gradient Edge Detection 8. 8 Zero-Crossing Edge Detector 8. 9 Integrated Directional Derivative Gradient Operator 8. 10 Corner Detection 8. 11 Isotropic Derivative Magnitudes 8. 12 Ridges and Ravines on Digital Images 8. 13 Topographic Primal Sketch DC & CV Lab. CSIE NTU 136

8. 10 Corner Detection l purpose l l l corners: to detect buildings in aerial images corner points: to determine displacement vectors from image pair corners with two conditions l l the occurrence of an edge significant changes in edge direction DC & CV Lab. CSIE NTU

Aerial Images Blackwell’s | Book store 138
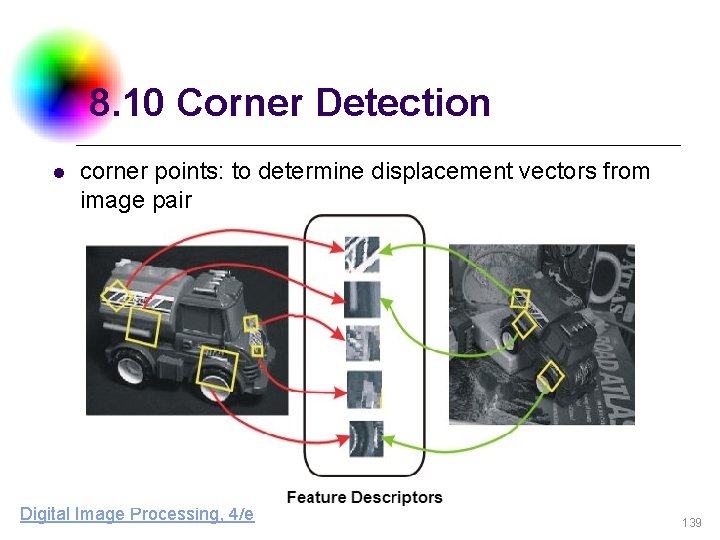
8. 10 Corner Detection l corner points: to determine displacement vectors from image pair Digital Image Processing, 4/e 139

8. 10 Corner Detection l corner points: to determine displacement vectors from image pair Digital Image Processing, 4/e 140
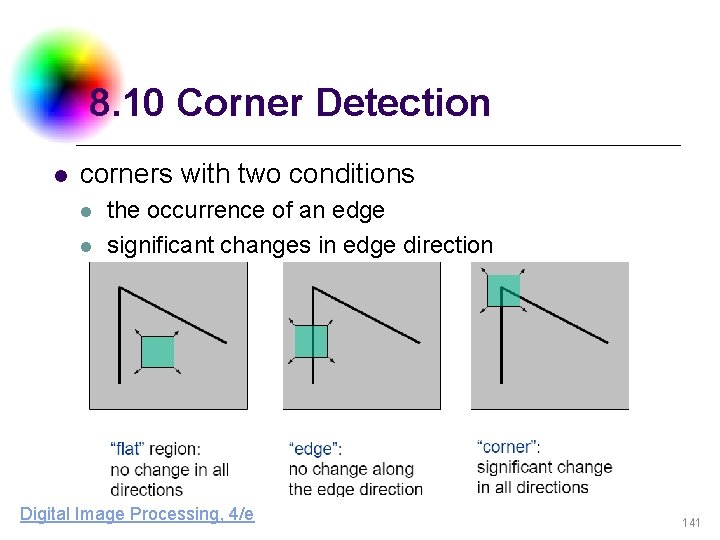
8. 10 Corner Detection l corners with two conditions l l the occurrence of an edge significant changes in edge direction Digital Image Processing, 4/e 141

8. 10 Corner Detection l DC & CV Lab. CSIE NTU 142

Outline l l l l 8. 1 Introduction 8. 2 Relative Maxima 8. 3 Sloped Facet Parameter and Error Estimation 8. 4 Facet-Based Peak Noise Removal 8. 5 Iterated Facet Model 8. 6 Gradient-Based Facet Edge Detection 8. 7 Bayesian Approach to Gradient Edge Detection 8. 8 Zero-Crossing Edge Detector 8. 9 Integrated Directional Derivative Gradient Operator 8. 10 Corner Detection 8. 11 Isotropic Derivative Magnitudes 8. 12 Ridges and Ravines on Digital Images 8. 13 Topographic Primal Sketch DC & CV Lab. CSIE NTU 143

8. 11 Isotropic Derivative Magnitudes l DC & CV Lab. CSIE NTU 144

8. 11 Isotropic Derivative Magnitudes l DC & CV Lab. CSIE NTU 145

8. 11 Isotropic Derivative Magnitudes l DC & CV Lab. CSIE NTU 146

8. 11 Isotropic Derivative Magnitudes l DC & CV Lab. CSIE NTU 147

Outline l l l l 8. 1 Introduction 8. 2 Relative Maxima 8. 3 Sloped Facet Parameter and Error Estimation 8. 4 Facet-Based Peak Noise Removal 8. 5 Iterated Facet Model 8. 6 Gradient-Based Facet Edge Detection 8. 7 Bayesian Approach to Gradient Edge Detection 8. 8 Zero-Crossing Edge Detector 8. 9 Integrated Directional Derivative Gradient Operator 8. 10 Corner Detection 8. 11 Isotropic Derivative 8. 12 Ridges and Ravines on Digital Images 8. 13 Topographic Primal Sketch DC & CV Lab. CSIE NTU 148

8. 12 Ridges and Ravines on Digital Images DC & CV Lab. CSIE NTU 149

8. 12 Ridges and Ravines on Digital Images l A digital ridge (ravine) occurs on a digital image when there is a simply connected sequence of pixels with gray level intensity values that are significantly higher (lower) in the sequence than those neighboring the sequence. l The facet model can be used to help accomplish ridge and ravine identification. DC & CV Lab. CSIE NTU

Outline l l l l 8. 1 Introduction 8. 2 Relative Maxima 8. 3 Sloped Facet Parameter and Error Estimation 8. 4 Facet-Based Peak Noise Removal 8. 5 Iterated Facet Model 8. 6 Gradient-Based Facet Edge Detection 8. 7 Bayesian Approach to Gradient Edge Detection 8. 8 Zero-Crossing Edge Detector 8. 9 Integrated Directional Derivative Gradient Operator 8. 10 Corner Detection 8. 11 Isotropic Derivative Magnitudes 8. 12 Ridges and Ravines on Digital Images 8. 13 Topographic Primal Sketch DC & CV Lab. CSIE NTU 151

8. 13 Topographic Primal Sketch 8. 13. 1 Introduction l We can categorize topography using functions. l Categories: l These categories have required invariance • • Peak Pit Ridge Ravine DC & CV Lab. CSIE NTU • Saddle • Flat • Hillside

8. 13. 2 Mathematical Classification of Topographic Structure l We will use the following notation to describe the mathematical properties of our topographic categories for continuous surfaces DC & CV Lab. CSIE NTU 153

8. 13. 2 Mathematical Classification of Topographic Structure l DC & CV Lab. CSIE NTU 154

8. 13. 2 Peak l DC & CV Lab. CSIE NTU

8. 13. 2 Peak l l : second directional derivative in direction DC & CV Lab. CSIE NTU

8. 13. 2 Pit l l pit (sink: bowl): local minimum in all directions pit: gradient zero, second directional derivative positive DC & CV Lab. CSIE NTU

8. 13. 2 Ridge l l l A ridge occurs on ridge line, a curve consisting of a series of ridge points and along ridge line, the points to the right and left are lower ridge line: may be flat, sloped upward, sloped downward, curved upward… ridge: local maximum in one direction DC & CV Lab. CSIE NTU

8. 13. 2 Ravine l l A ravine (valley): is identical to a ridge except that it is a local minimum in one direction walk along ravine line: points to the right and left are higher DC & CV Lab. CSIE NTU

8. 13. 2 Saddle local maximum in one direction, local minimum in perpendicular dir. l positive curvature in one direction, negative in perpendicular dir. l gradient magnitude zero l extrema of second directional derivative have opposite signs l DC & CV Lab. CSIE NTU

8. 13. 2 Flat l l l A flat (plain) is a simple, horizontal surface, must have zero gradient and no curvature. It satisfies the following conditions If the conditions are true, we may further classify a foot or a shoulder foot: flat begins to turn up into a hill shoulder: flat ending and turning down into a hill DC & CV Lab. CSIE NTU 161

8. 13. 2 Hillside l A hillside point is anything not covered by previous categories. hillside: nonzero gradient, no strict extrema Slope: tilted flat (constant gradient) l convex hill: curvature positive (upward) l l concave hill: curvature negative (downward) l DC & CV Lab. CSIE NTU

8. 13. 2 Hillside l saddle hill: up in one direction, down in perpendicular direction inflection point: zero crossing of second directional derivative l DC & CV Lab. CSIE NTU
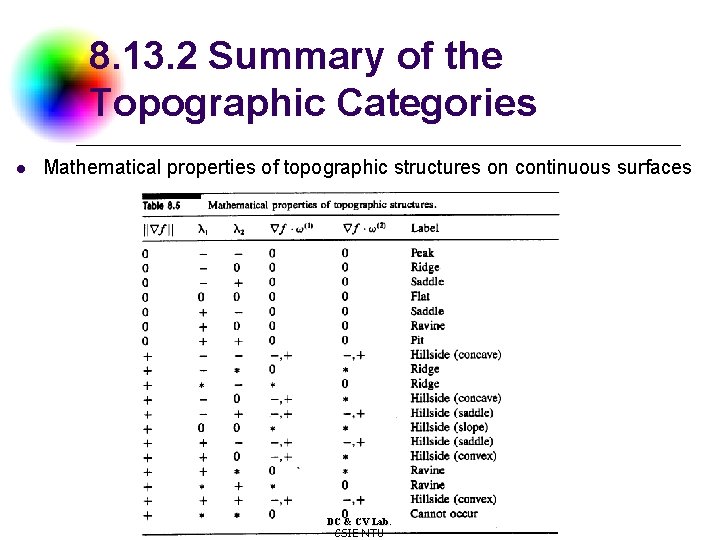
8. 13. 2 Summary of the Topographic Categories l Mathematical properties of topographic structures on continuous surfaces DC & CV Lab. CSIE NTU

8. 13. 2 Invariance of the Topographic Categories l l Invariant under monotonically increasing gray level transformations l Topographic labels (peak, pit, ridge, ravine, saddle, flat, and hillside) l Gradient direction l Directions of second directional derivative extrema Monotonically increasing: l positive derivative everywhere DC & CV Lab. CSIE NTU

8. 13. 3 Topographic Classification Algorithm l peak, pit, ridge, ravine, saddle: likely not to occur precisely at a pixel’s center l peak, pit, ridge, ravine, saddle: if within pixel area, carry the label l We search zero crossing of the first directional derivative, then decide the label of the pixel. DC & CV Lab. CSIE NTU

8. 13. 3 Case One: No Zero Crossing l No zero crossing along either of two directions: flat or hillside l l l If gradient zero, then flat If gradient nonzero, then hillside Hillside: possibly inflection point, slope, convex hill, concave hill, … DC & CV Lab. CSIE NTU

8. 13. 3 Case Two: One Zero Crossing l one zero crossing: peak, pit, ridge, ravine, or saddle DC & CV Lab. CSIE NTU
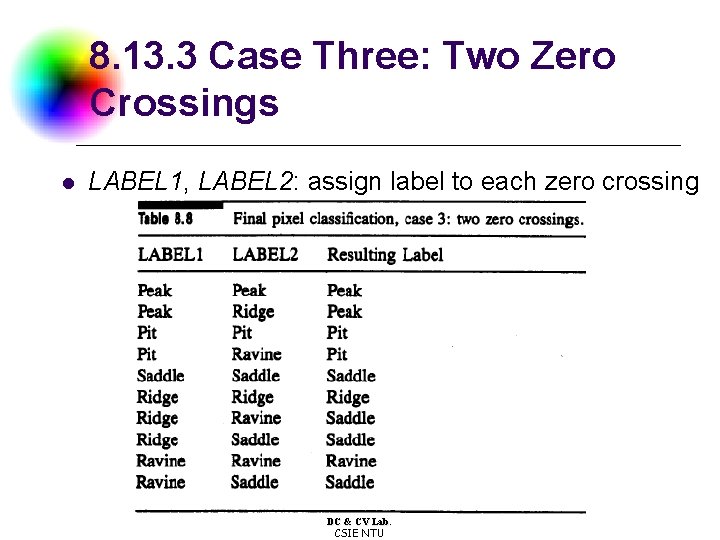
8. 13. 3 Case Three: Two Zero Crossings l LABEL 1, LABEL 2: assign label to each zero crossing DC & CV Lab. CSIE NTU

8. 13. 3 Case Four: More Then Two Zero Crossings l More than two zero crossings: l l Choose the one closest to pixel center After ignoring the other, same as case 3 DC & CV Lab. CSIE NTU

8. 13. 4 Summary of Topographic Classification Scheme l DC & CV Lab. CSIE NTU

l. END DC & CV Lab. CSIE NTU 172
- Slides: 173