COMPUTER 2430 Object Oriented Programming and Data Structures

COMPUTER 2430 Object Oriented Programming and Data Structures I 1

Sorting Algorithms The orders of algorithms, or the Big Os Selection Sort O(n 2) Bubble Sort O(n 2) Insertion Sort Worst Case: O(n 2) Average case: O(n 2) 2

Orders of Algorithms (Big Os) The order of an algorithm is the order of the fastest growing term (as n ). For example, O( 6 n 3 + 1200 n 2 + 100 n + 20 ) = O(n 3) O( 16 n 3 - n 2 + 2000 ) = O(n 3) Different coefficients (6 and 16) are ignored. Less significant terms are ignored Also known as the Time Complexity 3

Examples A un-sorted array of N elements • Finding if a target is in the array – Worst case is N steps – Average is N/2 – Both O(N) • Finding the max/min value in an array – O(N) • Calculating the average value – O(N) • Linear Search 4

Examples A regular array of N elements • Adding an element at the end – A few steps, no need to go over the array – Constant time – O(1) items[count] = obj; count ++; items[count ++] = obj; 5

Examples A regular array of N elements • Removing an element (at position index) and maintaining the order of remaining element by moving up elements – O(N) for (int i = index; i < count – 1; i ++) items[i] = items[i + 1]; count --; for (int i = index; i < count; i ++) items[i] = items[i + 1]; 6

Examples A regular array of N elements • Removing an element (at position index) without maintaining the order of remaining elements – O(1) items[index] = items[count - 1]; count --; items[index] = items[-- count]; 7

public class Stack { private Object[] items; private int top; // top is count public Stack ( int size ) { items = new Object[size]; top = 0; } public boolean is. Full() { return top == items. length; } public boolean is. Empty() { return top == 0; } } Big O: O(1) for is. Empty and is. Full. 8

public class Stack { private Object[] items; private int top; // top is count . . . public void push( Object obj ) { items[top ++] = obj; } } Big O: O(1) for push 9

public class Stack { private Object[] items; private int top; // top is count . . . public Object pop() { return items[-- top]; } } Big O: O(1) for pop 10

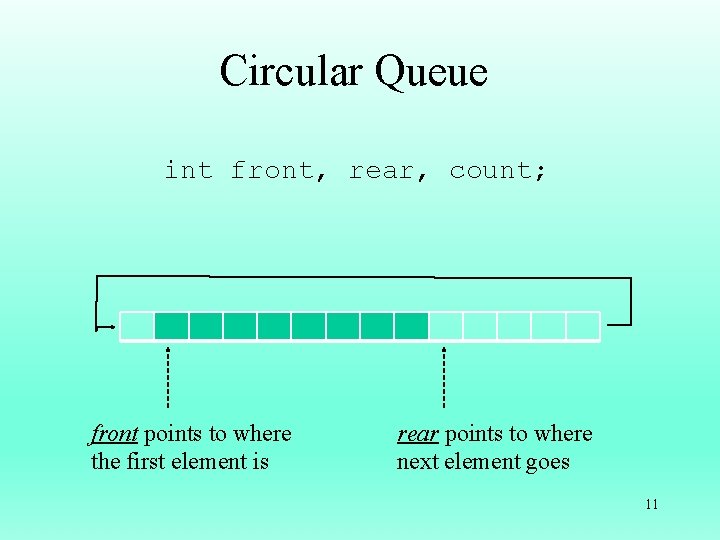
Circular Queue int front, rear, count; front points to where the first element is rear points to where next element goes 11

public class Queue { private Object[] items; private int front, rear, count; . . . // The constructor takes the saze (items. length) public Queue ( int size ) { items = new Object[size]; front = rear = count = 0; } } // class Queue 12

public class Queue { private Object[] items; private int front, rear, count; . . . public void add ( Object x ) { items[rear] = x; rear = (rear + 1) % items. length; count ++; } } // class Queue Big O: O(1) for add 13

public class Queue { private Object[] items; private int front, rear, count; . . . public Object remove () { Object obj = items[front]; front = (front + 1) % items. length; return obj; } } // class Queue Big O: O(1) for remove 14

Big Os O(1): not dependent on the number of items O(log N): much slower than O(N): linear time O(N * log N) O(N 2). . . O(2 N): exponential 15

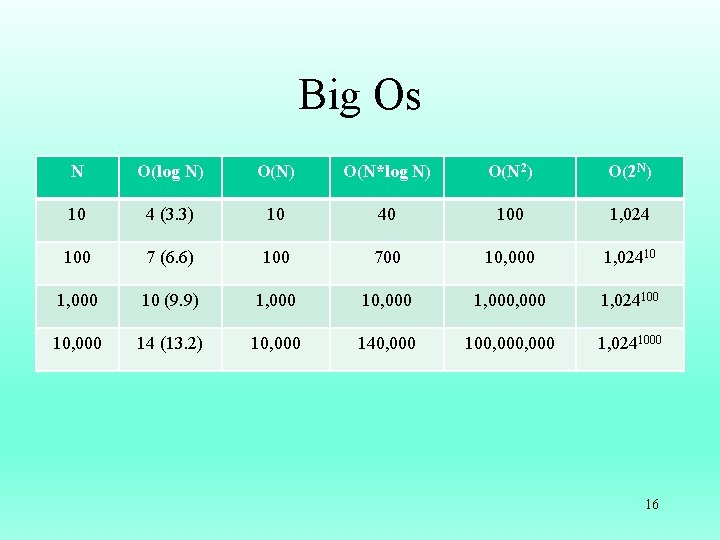
Big Os N O(log N) O(N*log N) O(N 2) O(2 N) 10 4 (3. 3) 10 40 100 1, 024 100 7 (6. 6) 100 700 10, 000 1, 02410 1, 000 10 (9. 9) 1, 000 10, 000 1, 024100 10, 000 14 (13. 2) 10, 000 140, 000 100, 000 1, 0241000 16

Formula How many items? Step is a non-zero integer s s+step s+2*step. . . t-2*step t-step t (t – s) / step + 1 (last – first) / step + 1 18

Counting: What is the sum? 1 + 2 + 3 +. . . + (n-3) + (n– 2) + (n-1) + S = 1 + 2 + 3 +. . . +(n-3)+(n– 2)+(n-1) S = (n-1)+(n-2)+(n-3)+. . . + 3 + 2 + 1 2*S = n + n = n * (n-1) + n +. . . + n + n S = n * (n – 1) / 2 = (first + last) * (number of items) / 2 19

Counting: What is the sum? How many items? n – t + 1 t + (t+1) + (t+2) +. . . + (n-2) + (n-1) + n + S = t n + (t+1) + (t+2) +. . . + (n-2) + (n-1) + n + (n-1) + (n-2) +. . . + (t+2) + (t+1) + t 2*S = (t+n) +. . . + (t+n) = (t+n) * (n-t+1) S = (t + n) * (n – t + 1) / 2 = (first + last) * (number of items) / 2 20

Math Formulas 1 + 2 + 3 +. . + r = (1 + r) * r / 2 t + (t+1) + (t+2) +. . + r = (t+r) * (r-t+1) / 2 = (first + last) * (number of items) / 2 21

Exercise Counting Turn in Monday in class Five Bonus Points 22

Quiz 5 • • Wednesday, Nov 28 Sorting Big Os Counting 23

Prog 5 Due Monday, Nov 26 Grace Wednesday, Nov 28 (-5) 24