Computations for growth models Plotting exponential growthdecline curve

Computations for growth models

Plotting exponential growth/decline curve Matlab commands: clear all % figures for exponential growth/decline tim=[0: 0. 1: 20]; r=0. 1; N_0=100; N=N_0*exp(r*tim); plot(tim, N, 'k')

Using Matlab function ode 45 for computing solution to logistic equation Matlab commands: clear all % environmental capacity K=500; % Initial population size N 0=1; % growth rate r=0. 1; % time scale tim=0: 0. 1: 100;

% analytic solution to logistic differential equaiton for ki=1: length(tim) N(ki)=K/(1+(K/N 0 -1)*exp(-r*tim(ki))); end % Now we compute the same using ode 45 % and the function 'lgf' which defines logistic model [Tode, Node]=ode 45('lgf', [0 100], 1); % compare two curves plot(tim, N, Tode, Node, 'or')

Matlab function ‘lgf’ used in the above procedure ‘ode 45’ % function lgf function d. N=lgf(T, N) r=0. 1; K=500; d. N=r*N*(1 -N/K);

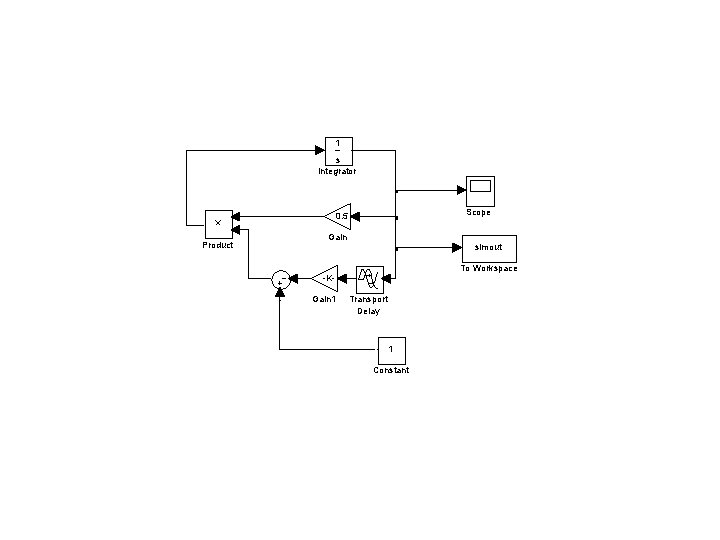
Simulink block diagram for logistic model with delay in environmental limiting action

1 s Integrator Scope 0. 5 Product Gain simout To Workspace -KGain 1 Transport Delay 1 Constant

Fitting model parameters to data Method of least squares, find (estimate) X Size(B) = n x 1, Size(A) = n x k, Size(X) = k x 1, n > k T – matrix transposition Matlab function to compute X: X=AB

Data on world population http: //www. census. gov/ipc/www/world. html

Fitting exponential model to data on world population - 1 Data written in Matlab format: clear all popdt=[-10000 1; -4000 7; -500 100; 200 190; 700 207; 1100 301; 1340 443; 1650 470; 1850 1128; 1930 2070; tim=popdt(: , 1); popul=popdt(: , 2); -8000 5; -3000 14; -400 162; 400 190; 800 220; 1200 360; 1400 350; 1700 600; 1900 1550; 1940 2300; -6500 -200 500 900 1250 1500 1750 1910 1950 5; 27; 150; 190; 226; 400; 425; 629; 1750; 2400]; -5000 5; -1000 50; 1 170; 600 200; 1000 254; 1300 360; 1600 545; 1800 813; 1920 1860;

A=[tim ones(size(tim))]; B=log(popul); % our estimated parameters PAR=AB % now let us see how our estimates compare to data for kk=1: length(B) ppl(kk)=PAR(1)*tim(kk)+PAR(2); end plot(tim, ppl, tim, log(popul), 'or') pause % or plot(tim, exp(ppl), tim, popul, 'or')

Fitting exponential model to data on world population - 2 Use of Matlab function ‘fmins’ to minimize over arguments Matlab commands: % find parameters estimates QPAR=fmins('wp_fun', [0. 0006 5]) % now let us see how our estimates compare to data for kk=1: length(tim) qppl(kk)=exp(QPAR(1)*tim(kk)+QPAR(2)); end plot(tim, log(qppl), tim, log(popul), 'or') pause % or plot(tim, qppl, tim, popul, 'or')

More data USA population 1790 – 2000: http: //fisher. lib. virginia. edu/census/ Chinese children growth charts: http: //www. fwcc. org/growthchart. html