Computational thinking algorithms and programming Computer Science Hexadecimal

Computational thinking, algorithms and programming Computer Science Hexadecimal Conversions 2. 6 – Representing Data

Computational thinking, algorithms and programming Computer Science What is Hexadecimal? Hexadecimal is a base 16 number system: there are 16 digits, 0 to 15. As we have only 10 single digits (0 -9), we use upper-case letters A to F for the remaining digits. Therefore, hexadecimal digits are represented as: 0123456789 ABCDEF

Computational thinking, algorithms and programming Computer Science Why do we need Hexadecimal? We need hexadecimal numbers because of our human limitations. Computers do not use or understand hexadecimal, only binary. Hexadecimal is used because we get confused with large binary numbers, so we simplify them by representing them in hexadecimal notation. If we tried to give our phone number to someone in binary, it would be really difficult, therefore humans need an easier method. Since a byte is 8 -bits, it makes sense to divide that binary number into two 4 -bit numbers. Since 4 -bits gives you a possible range of 0 -15, a Base 16 system is easier to work with. Lets look at an example…

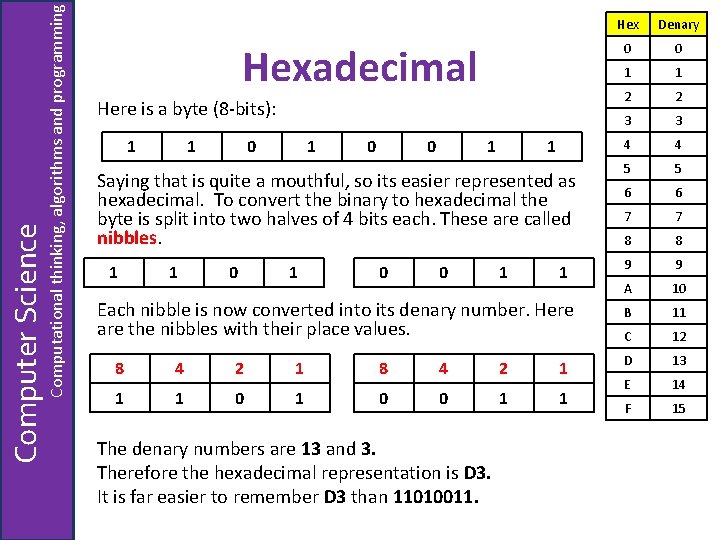
Computational thinking, algorithms and programming Computer Science Hexadecimal Number system Hex Denary 0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 A 10 B 11 C 12 D 13 E 14 F 15 Remember that in denary (Base 10) we only have 10 single digits available to us… therefore, for Base 16 we use this representation.

Computational thinking, algorithms and programming Computer Science Hexadecimal Here is a byte (8 -bits): 1 1 0 0 1 1 Saying that is quite a mouthful, so its easier represented as hexadecimal. To convert the binary to hexadecimal the byte is split into two halves of 4 bits each. These are called nibbles. 1 1 0 0 1 1 Each nibble is now converted into its denary number. Here are the nibbles with their place values. 8 4 2 1 1 1 0 0 1 1 The denary numbers are 13 and 3. Therefore the hexadecimal representation is D 3. It is far easier to remember D 3 than 11010011. Hex Denary 0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 A 10 B 11 C 12 D 13 E 14 F 15

Computational thinking, algorithms and programming Computer Science Lets have a go… a) b) c) d) e) f) g) 1000 0111 0101 0001 1000 0110 1001 1111 1011 0110

Computational thinking, algorithms and programming Computer Science Answers… a) b) c) d) e) f) g) 1000 0111 0101 0001 1000 0110 1001 1111 1011 0110 87 75 18 6 E 9 F BB 66

Computational thinking, algorithms and programming Computer Science Converting denary to hexadecimal Here is denary number 213. To convert to hexadecimal, we must progressively divide by 16 until the result is 0 and remember the remainders. 213 ÷ 16 = 13 (remainder 5) 13 = D D 5 5=5 Hex Denary 0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 A 10 B 11 C 12 D 13 E 14 F 15

Computational thinking, algorithms and programming Computer Science Lets have a go… a) b) c) d) e) f) g) 226 98 13 57 198 207 136

Computational thinking, algorithms and programming Computer Science Answers… a) b) c) d) e) f) g) 226 98 13 57 198 207 136 E 2 62 D 39 C 6 CF 88