Computational Solid State Physics 5 5 Band offset

Computational Solid State Physics 計算物性学特論　5回 5. Band offset at hetero-interfaces 　　and effective mass approximation

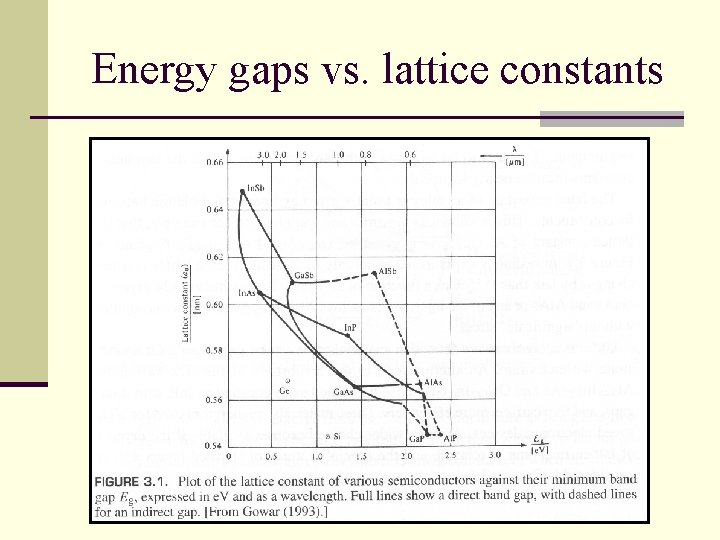
Energy gaps vs. lattice constants

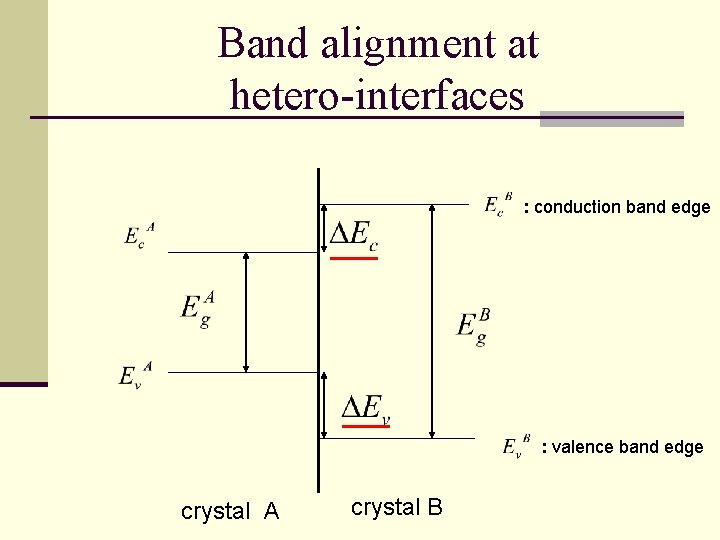
Band alignment at hetero-interfaces : conduction band edge : valence band edge crystal A crystal B

Anderson’s rule for the band alignment (1) χ: electron affinity None of the interface effects are considered.

Anderson’s rule for the band alignment (2) : conduction band offset : valence band offset

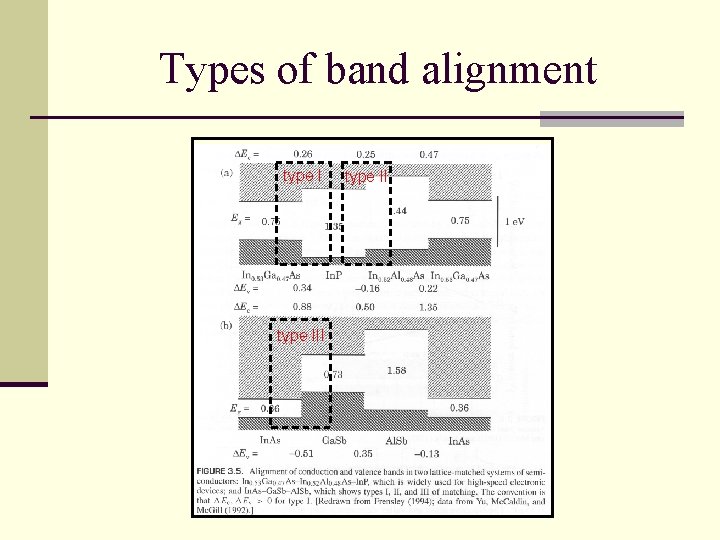
Types of band alignment type III type II

Band bending in a doped hetero-junction (1)

Band bending in a doped hetero-junction (2)

Effective mass approximation ・Suppose that a perturbation 　 is added to a perfect crystal. ・How is the electronic state? Examples of perturbations an impurity, a quantum well, barrier, superlattice, potential from a patterned gate, space charge potential

Effective mass approximation (1) V : external potential : Bloch function assume: conduction band 　　　　　　n is minimum at k=0

Effective mass approximation(2)

Effective mass approximation(3) If Schroedinger equation for envelope function χ(r)

Effective mass approximation (4) ・Schroedinger equation for an envelope 　function χ(r) All the effects of crystal potential are included in εc and effective mass m*.

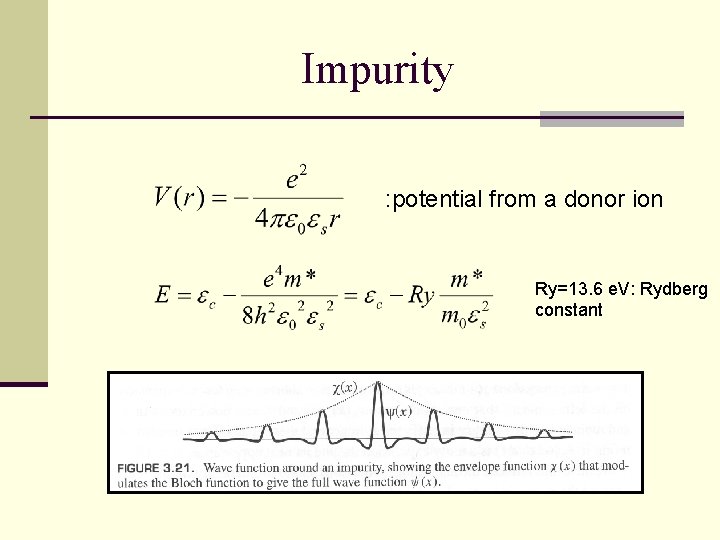
Impurity : potential from a donor ion Ry=13. 6 e. V: Rydberg constant

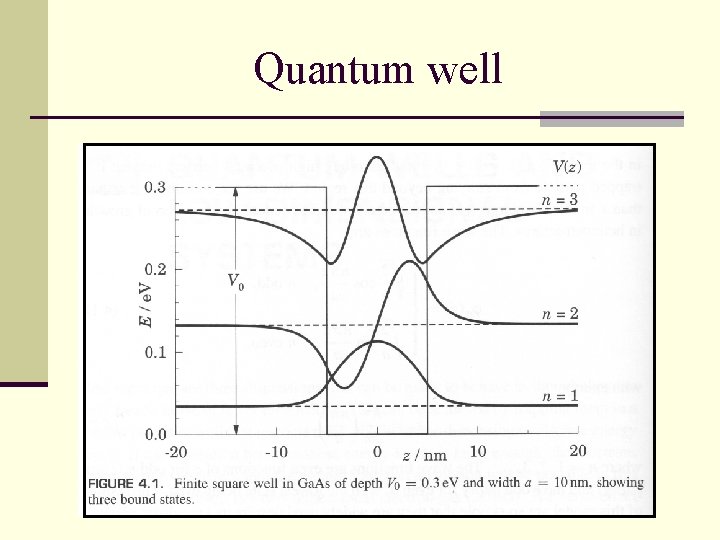
Quantum well

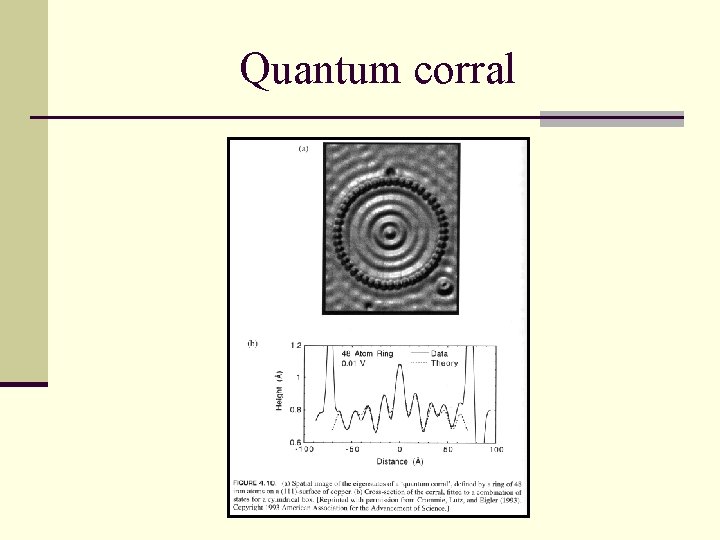
Quantum corral

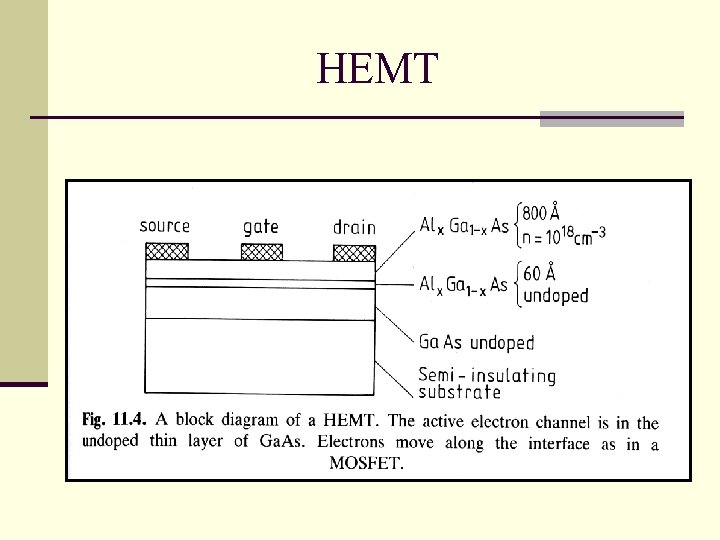
HEMT

2 D-electron confinement in HEMT The sub-band structure at the interface of the Ga. As active channel in a HEMT structure. E 1 and E 2 are the confined levels. The approximate positions of E 1 and E 2 as well as the shape of the wave functions are indicated in the lower part of the diagram. In the uper part, an approximate form of the potential profile is shown, including contributions of the conduction band offset and of the space charge potential.

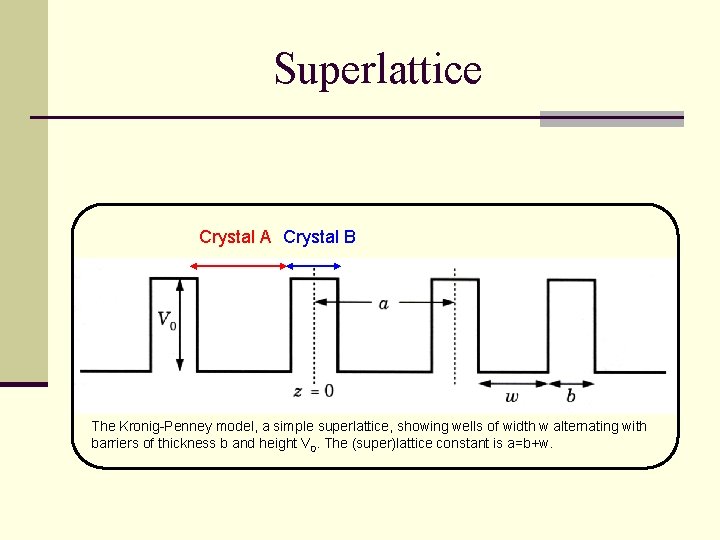
Superlattice Crystal A Crystal B The Kronig-Penney model, a simple superlattice, showing wells of width w alternating with barriers of thickness b and height V 0. The (super)lattice constant is a=b+w.

Kronig-Penny model (1) Schroedinger equation in the effective mass approximation Bloch condition for superlattice k: wave vector of Bloch 　 function in the superlattice

Kronog-Penney model (2) Boundary condition at x=0 (1)continuity of wavefunction (2)connection condition for the 1 st derivative of wavefunction (2’) Solution of Schroedinger equation for

Kronig-Penney model (3) (1) (2’) Simultaneous equation for E(k)

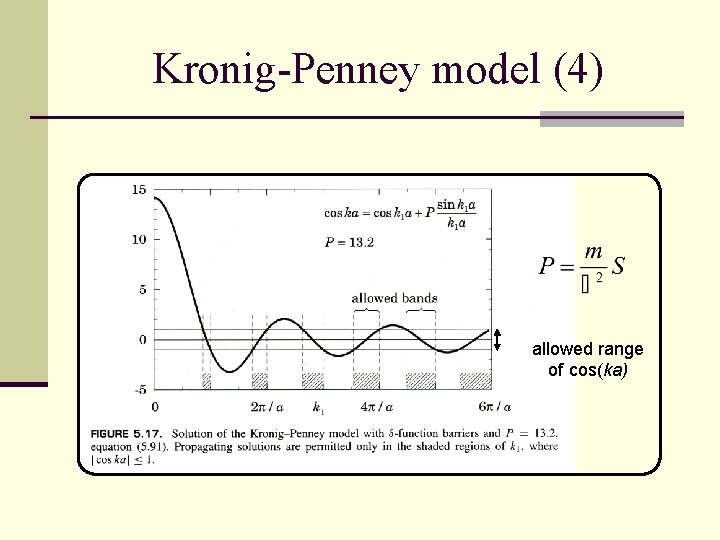
Kronig-Penney model (4) allowed range of cos(ka)

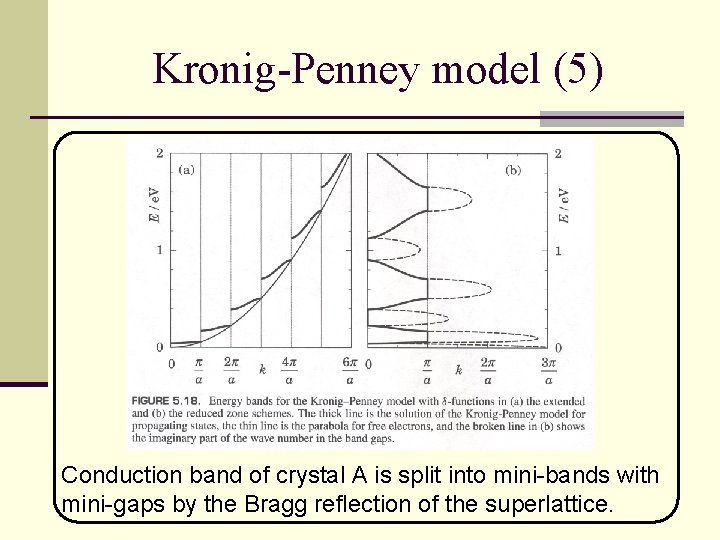
Kronig-Penney model (5) Conduction band of crystal A is split into mini-bands with mini-gaps by the Bragg reflection of the superlattice.

Problems 5 n Calculate the lowest energy level for electrons and light and heavy holes in a Ga. As well 6 nm wide sandwiched between layers of Al 0. 35 Ga 0. 65 As. Calculate the photoluminescence energy of the optical transition. n Calculate the two-dimensional Schroedinger equation for free electrons confined in a cylindrical well with infinitely high walls for r>a.