Computational Solid State Physics 4 Electronic structure of

Computational Solid State Physics 計算物性学特論 第４回 4. Electronic structure of crystals

Single electron Schroedinger equation m: electron mass V(r): potential energy h: Planck constant Expansion by base functions Φn : overlap integral

: algebraic equation : matrix element of Hamiltonian

: expression of algebraic equation by matrixes and vectors

Solution (1) : ortho-normalized bases eigenvalue equation condition of existence of inverse matrix of secular equation : unit matrix

Solution (2)

Potential energy in crystals : periodic potential a, b, c: primitive vectors of the crystal n. l. m: integers G: reciprocal lattice vectors Fourier transform of the periodic potential energy

Primitive reciprocal lattice vectors Properties of primitive reciprocal lattice vectors Volume of 1 st Brilloluin zone : volume of a unit cell

Bloch’s theorem for wavefunctions in crystal (1) (2) k is wave vectors in the 1 st Brillouin zone. Equations (1) and (2) are equivalent.

Plane wave expansion of Bloch functions G : reciprocal lattice vectors

Normalized plane wave basis set : satisfies the Bloch’s theorem V : volume of crystal

Schroedinger equation for single electron in crystals : potential energy in crystal : secular equation to obtain the energy eigenvalue at k. : Bragg reflection

Energy band structure of metals

Zincblende structure c b a

Brillouin zone for the zincblende lattice

Energy band of Si, Ge and Sn Si Ge Sn Empirical pseudopotential method

Tight-binding approximation Linear Combination of Atomic Orbits (LCAO) i-th atomic wavefunction at (n, l, m)-lattice sites satisfies the Bloch theorem.

1 -dimensional lattice (1) a S(n-m)

1 -dimensional lattice (2) : Schroedinger equation

1 -dimensional lattice (3) Energy dispersion relation 1 st Brillouin zone ε 0=H 00: site energy t=H 10=H-10: transfer energy t<0 ε(k)/-t ka

Valence orbits for III-V compounds 4 bonds

Matrix elements of Hamiltonian between atomic orbits

Matrix element of Hamiltonian between atomic orbit Bloch functions

Calculation of Hamiltonian matrix element

Matrix element between atomic orbits

Hamiltonian matrix for the zincblende structure

Energy at Gamma point (k=0) 1 -fold 3 -fold Bottom of conduction band: s-orbit Top of valence band: p-orbit

Energy band of Germanium

Energy band of Ga. As, Zn. Se, In. Sb, Cd. Te

Spin-orbit splitting at band edge

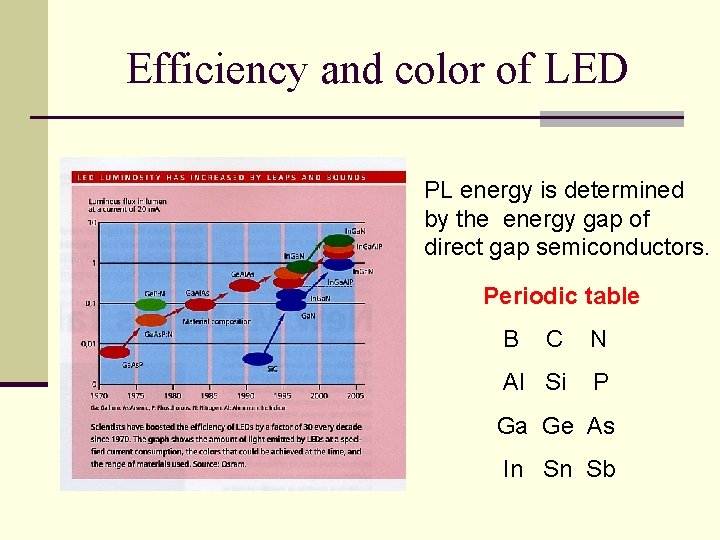
Efficiency and color of LED PL energy is determined by the energy gap of direct gap semiconductors. Periodic table B C N Al Si P Ga Ge As In Sn Sb

Bond picture (1): sp 3 hybridization [111] [-1 -1 -1] [-1 -11]

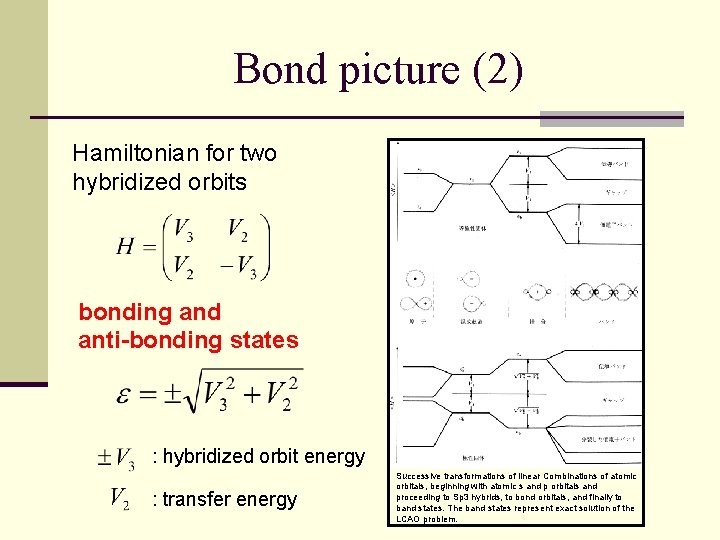
Bond picture (2) Hamiltonian for two hybridized orbits bonding and anti-bonding states : hybridized orbit energy : transfer energy Successive transformations of linear Combinations of atomic orbitals, beginning with atomic s and p orbitals and proceeding to Sp 3 hybrids, to bond orbitals, and finally to band states. The band states represent exact solution of the LCAO problem.

Problems 4 n Calculate the free electron dispersion relation within the 1 st Brillouin zone for diamond structure. n Calculate the energy dispersion relation for a graphen sheet, using a tight-binding approximation. n Calculate the dispersion relation for a graphen sheet, using pane wave bases.