Computational Molecular Biology Group Testing Pooling Designs Group

Computational Molecular Biology Group Testing – Pooling Designs

Group Testing (GT) Ø Definition: q Given n items with at most d positive ones q Identify all positive ones by the minimum number of tests Ø Each test is on a subset of items Ø Positive test outcome: there exists a positive item in the subset My T. Thai mythai@cise. ufl. edu 2

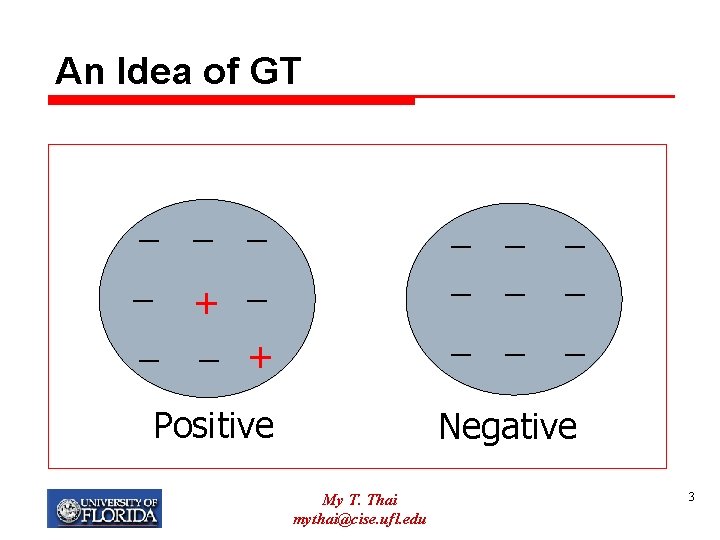
An Idea of GT _ _ _ + Positive _ _ _ _ _ Negative My T. Thai mythai@cise. ufl. edu 3

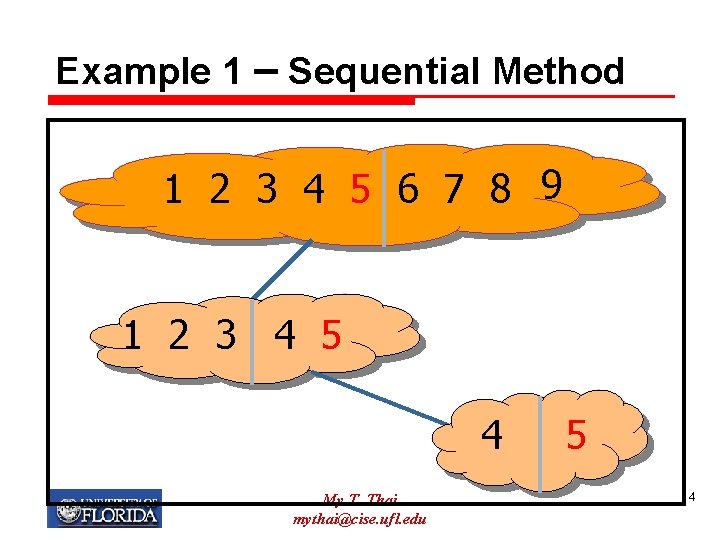
Example 1 – Sequential Method 1 2 3 4 5 6 7 8 9 1 2 3 4 5 4 My T. Thai mythai@cise. ufl. edu 5 4

Example 2 – Non-adaptive Method P 4 p 5 p 6 p 1 1 2 3 p 2 4 5 6 p 3 7 8 9 Non-adaptive group testing is called pooling design in biology My T. Thai mythai@cise. ufl. edu 5

Sequential and Non-adaptive Ø Sequential GT needs less number of tests, but longer time. Ø Non-adaptive GT needs more tests, but shorter time. Ø In molecular biology, non-adaptive GT is usually taken. Why? My T. Thai mythai@cise. ufl. edu 6

Because… Ø The same library is screened with many different probes. It is expensive to prepare a pool for testing first time. Once a pool is prepared, it can be screened many times with different probes. Ø Screening one pool at a time is expensive. Screening pools in parallel with same probe is cheaper. Ø There are constrains on pool sizes. If a pool contains too many different clones, then positive pools can become too dilute and could be mislabeled as negative pools. My T. Thai mythai@cise. ufl. edu 7

Pooling Designs Ø Problem Definition q Given a set of n clones with at most d positive clones q Identify all positive clones with the minimum number of tests Ø Pool: a subset of clones Ø Positive pool: a pool contains at least one positive clone Ø Clones = Items My T. Thai mythai@cise. ufl. edu 8

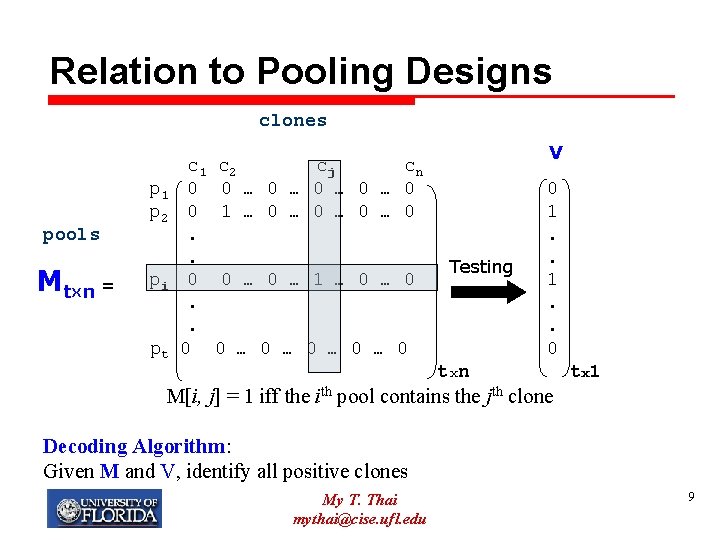
Relation to Pooling Designs clones pools M tx n = c 1 p 1 0 p 2 0. . pi 0. . pt 0 V c 2 cj cn 0 … 0 … 0 1 … 0 … 0 0 … 1 … 0 Testing 0 … 0 … 0 0 1. . 0 txn t x 1 M[i, j] = 1 iff the ith pool contains the jth clone Decoding Algorithm: Given M and V, identify all positive clones My T. Thai mythai@cise. ufl. edu 9

Observation clones pools p 1 p 2 p 3 c 1 1 0 0 c 2 1 0 0 0 1 0 c 3 1 0 0 1 cj 0 0 1 1 1 0 0 1 0 0 0 1 0 0 1 Observation: All columns are distinct. To identify up to d positives, all unions of up to d columns should be distinct! Union of d columns: Boolean sum of these d columns My T. Thai mythai@cise. ufl. edu 10

Challenges Ø Challenge 1: How to construct the binary matrix M such that: q Outputs of any union of d columns are distinct Ø Challenge 2: How to design a decoding algorithm with efficient time complexity [O(tn)] My T. Thai mythai@cise. ufl. edu 11

d-separable Matrix clones pools p 1 p 2 p 3 pi pt c 1 0 0 1 0. . 0 c 2 c 3 0 0 … 0 1 0 … 0 … 0 0 1 … 0 … … 0 0 cj … 0 … 0 … … … … 0 0 0 0 … … cn 0 0 0 … 0 … 1 … 0 … 0 0 0 … 0 … 0 All unions of d columns are distinct. My T. Thai mythai@cise. ufl. edu 12

d-separable Matrix clones pools p 1 p 2 p 3 pi pt c 1 0 0 1 0. . 0 c 2 c 3 0 0 … 0 1 0 … 0 … 0 0 1 … 0 … … 0 0 cj … 0 … 0 … … … … 0 0 0 0 … … cn 0 0 0 … 0 … 1 … 0 … 0 0 0 … 0 … 0 All unions of up to d columns are distinct. Decoding: O(nd) My T. Thai mythai@cise. ufl. edu 13

d-disjunct Matrix Ø Definition: An binary matrix Mtxn is a ddisjunct matrix (d < t) if: q The union of any d columns does not contain any other column Ø Example: A 2 -disjunct matrix M = 1 0 0 0 1 My T. Thai mythai@cise. ufl. edu 14

d-disjunct Matrix (cont) Ø d-disjunct matrix can efficiently identify up to d positive clones. Why? Ø Theorem 1: All unions of d distinct columns are distinct (thus d-disjunct implies d-separable) Ø Theorem 2: The number of clones not in negative pools is always at most d q Corollary 1: The tests of negative outputs determine all negative clones q Decoding time complexity: O(tn) My T. Thai mythai@cise. ufl. edu 15

Proof of Theorem 2 Ø Note that an item does not appearing in any negative pool iff its corresponding column is contained by the union of d positive columns Ø Therefore, the number of items not appearing in any negative pool is more than d iff there at least a non-positive item whose column is contained by the d positive columns Ø But M is d-disjunct, hence Theorem 2 follows My T. Thai mythai@cise. ufl. edu 16

Decoding Algorithm Input: d-disjunct matrix M and output vector V Output: All positive clones for each clone c in n clones if c is in a negative pool remove c return remaining clones c 1 c 2 c 3 c 4 c 5 c 6 p 1 1 0 0 0 1 P 2 1 0 0 1 1 0 0 P 3 0 1 0 1 0 P 4 0 0 1 1 1 My T. Thai mythai@cise. ufl. edu 17

Fields Ø Field: is any set of elements that satisfies the field axioms for both addition and multiplication and is a division algebra Ø Eg: Compex, Rational, Real My T. Thai mythai@cise. ufl. edu 18

Division Algebra My T. Thai mythai@cise. ufl. edu 19

Finite Fields Ø Finite Field: q is a field with a finite field order, i. e. , number of elements. q The order of a finite field is always a prime or a prime power (power of a prime) § Eg: 16 = 2^4 is a prime power where 6, 15 are not Ø Eg: in GF(5), 4+3=7 is reduced to 2 modulo 5 My T. Thai mythai@cise. ufl. edu 20

How to construct a d-disjunct matrix Consider a finite field GF(q). Choose s, q, k satisfying: Step 1: Construct matrix Asxn as follows: for x from 0 to s -1 for each polynomials pj of degree k A[x, pj] = pj(x) p 1 A= p 2 pj p 2(x) pj(x) pn 0 1 x s-1 My T. Thai mythai@cise. ufl. edu 21

Algorithm (cont) Step 2: Construct matrix Btxn from Asxn as follows: for x from 0 to s -1 for y from 0 to q -1 for each polynomials pj of degree k if A[x, pj] = = y B[(x, y), pj] = 1 else B[(x, y), pj] = 0 p 2(x) ≠ y p 1 p 2 pj 0 1 pn p 1 pj(x) = y p 2 pj 0 1 pn (0, 0) (0, 1) A= x s-1 p 2(x) pj(x) B = (x, y) My T. Thai (s-1, q-1) mythai@cise. ufl. edu 22

Algorithm Analysis Ø Theorem 3: (Correctness) If kd ≤ s ≤ q, then Btxn is ddisjunct. Ø Theorem 4: The number of tests t obtained from this algorithm is t = qs = O(q 2) where: My T. Thai mythai@cise. ufl. edu 23

Errors in Experiments Ø False negative: q Pool contains some positive clones q But return the negative outcome Ø False positive: q Pool contains all negative clones q But return the positive outcome My T. Thai mythai@cise. ufl. edu 24

An e-Error Correcting Model Ø Definition: q Assume that there is at most e errors in testing q All positive clones can still be identified Ø Hamming distance: the Hamming distance of two column vectors is the number of different components between them Ø e-error-correcting: A matrix is said to be e-errorcorrecting if the Hamming distance of any two unions of d columns is at least 2 e + 1 My T. Thai mythai@cise. ufl. edu 25

(d, e)-disjunct Matrix Ø Definition: An t × n binary matrix M is (d, e)disjunct if for any one column j and any other d columns j 1, j 2, . . . , jd, there exist e + 1 rows i 0, i 2, … , ie such that Miuj = 1 and Miujv = 0 for u = 0, 1, …, e and v = 1, 2, . . . , d My T. Thai mythai@cise. ufl. edu 26

E-error Correcting Ø Theorem 5: For every (d, k)-disjunct matrix, the Hamming distance between any two unions of d columns is at least 2 k + 2 My T. Thai mythai@cise. ufl. edu 27

Theorem 6 Ø Theorem 6: Suppose testing is based on a (d, e) -disjunct matrix. If the number of errors is at most e, then the number of negative pools containing a positive item is always smaller than the number of negative pools containing a negative item My T. Thai mythai@cise. ufl. edu 28

Proof of Theorem 6 Ø Let i be a positive item, j be a negative item. Suppose #negative pools containing i = m. Then m pools must receive errors. Hence, there at most e – m error tests turning negative outcome to positive outcome. Moreover, if no error exists, # negative pools containing j is at least e + 1 due to (d, e)-disjunct. Hence #negative pools containing j is at least (e+1)-(e-m) = m +1>m My T. Thai mythai@cise. ufl. edu 29

Decoding in e-error-correcting Ø Corollary: From Theorem 6, we see that to decode positives from testing based on (d, e)disjuct matrix, we only need to compute the number of negative pools containing each item and select d smallest one. This runs in time O(nt) My T. Thai mythai@cise. ufl. edu 30

Decoding Algorithm with e Errors T = empty set for each clone ci (i = 1…n) t(ci) = # negative pools containing ci T=T t(ci) end for Let Td = set of d smallest t(ci) in T return ci if t(ci) in Td Time complexity: O(tn) My T. Thai mythai@cise. ufl. edu 31