Computational methods in physics 1 Introduction to Lattice


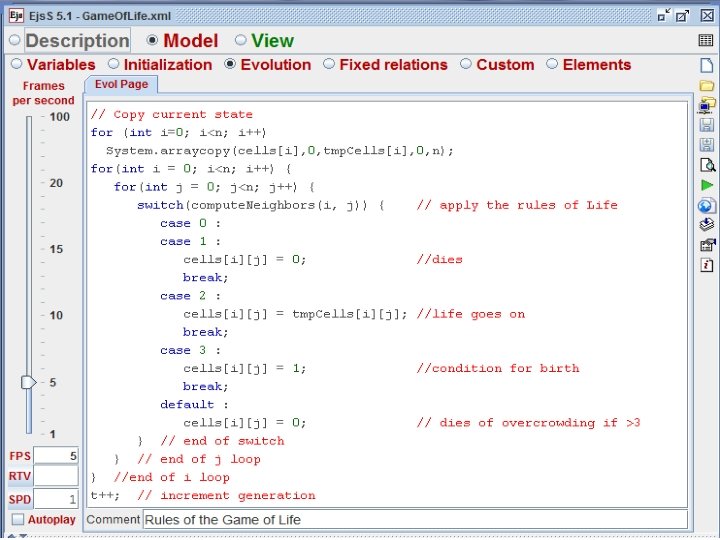
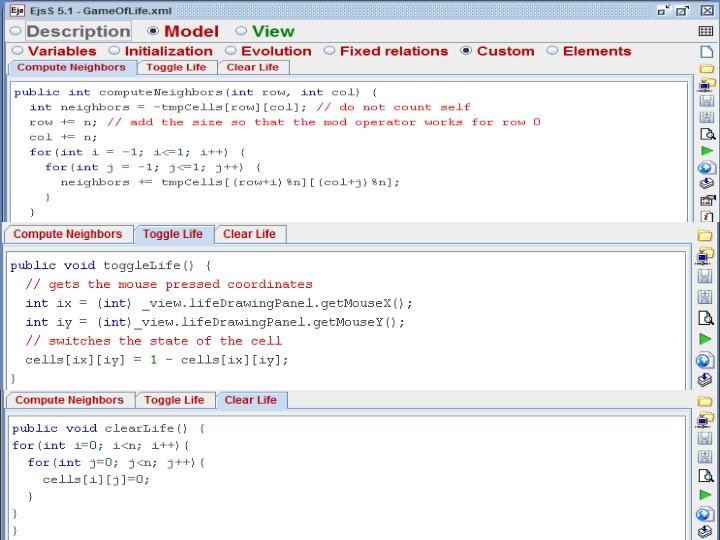
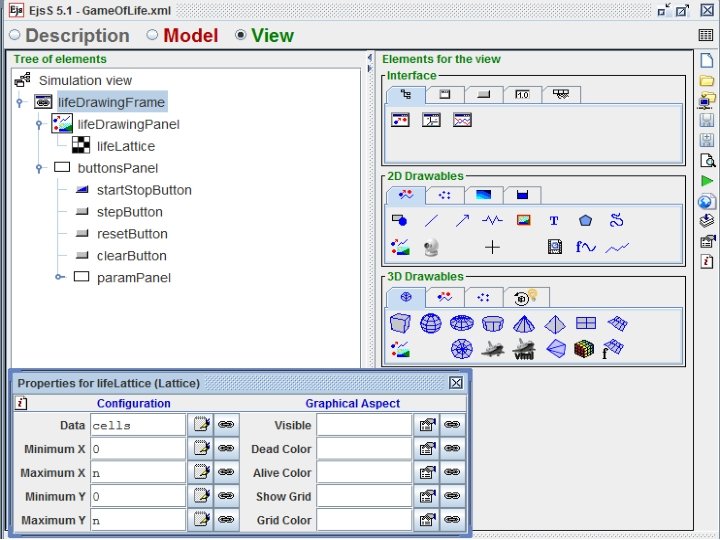



- Slides: 26

Computational methods in physics

1 Introduction to Lattice Models Introduction to Easy Java Simulations software 2 Deterministic cellular automata Conway model 3 Monte-Carlo method Ising model 4 Random and selfavoiding walk Brownian motion and diffusion 5 Percolation theory Site square model 6 Pattern and dendrite growth

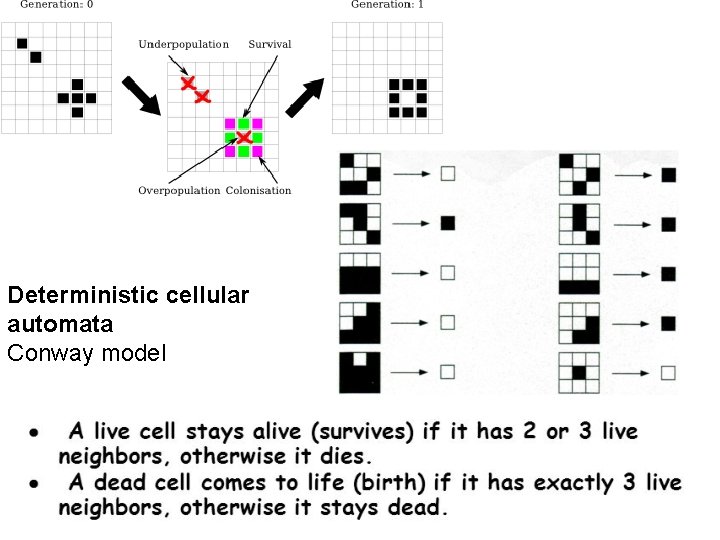
Deterministic cellular automata Conway model


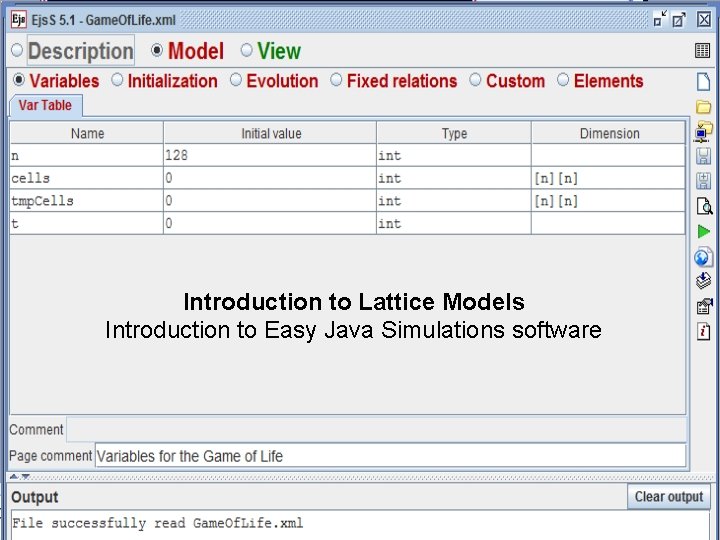
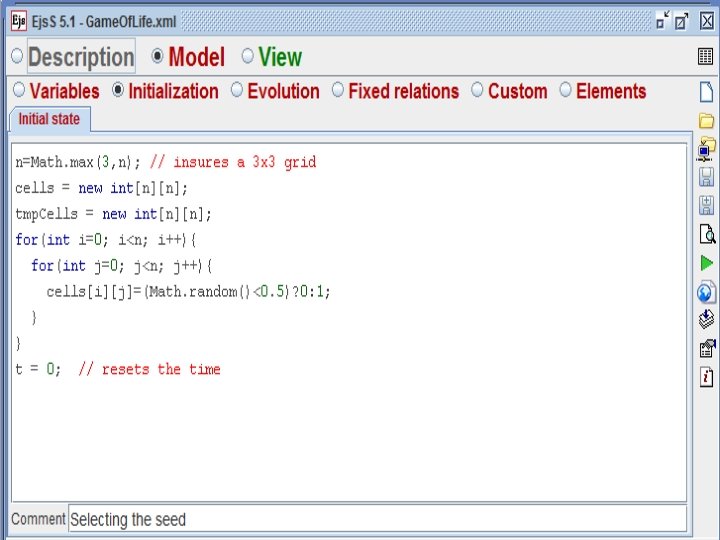
Introduction to Lattice Models Introduction to Easy Java Simulations software





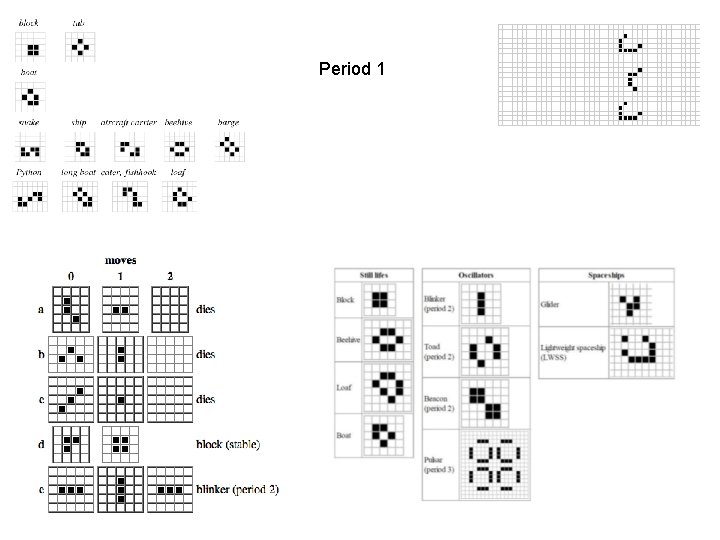
Period 1

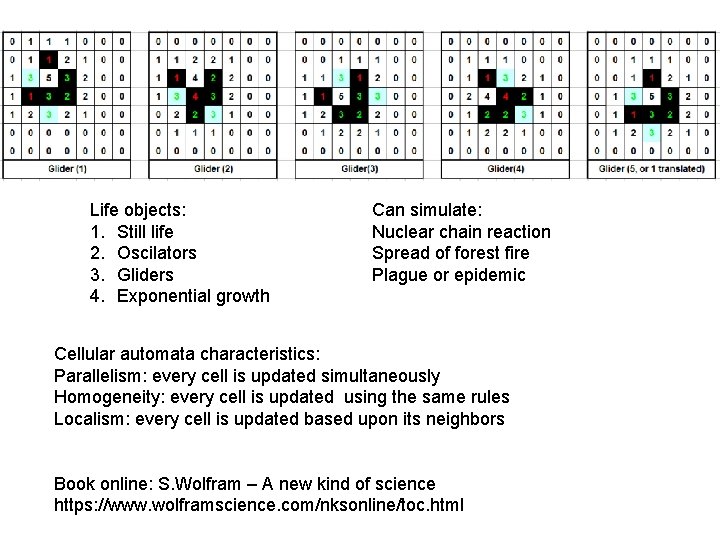
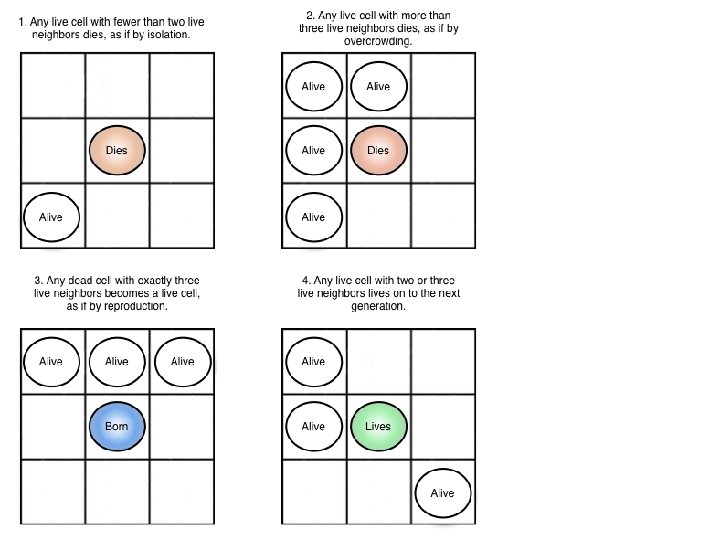
Life objects: 1. Still life 2. Oscilators 3. Gliders 4. Exponential growth Can simulate: Nuclear chain reaction Spread of forest fire Plague or epidemic Cellular automata characteristics: Parallelism: every cell is updated simultaneously Homogeneity: every cell is updated using the same rules Localism: every cell is updated based upon its neighbors Book online: S. Wolfram – A new kind of science https: //www. wolframscience. com/nksonline/toc. html

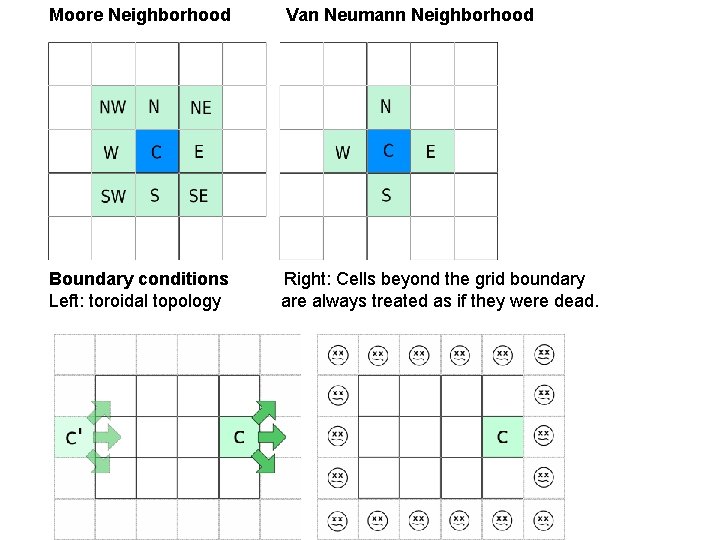
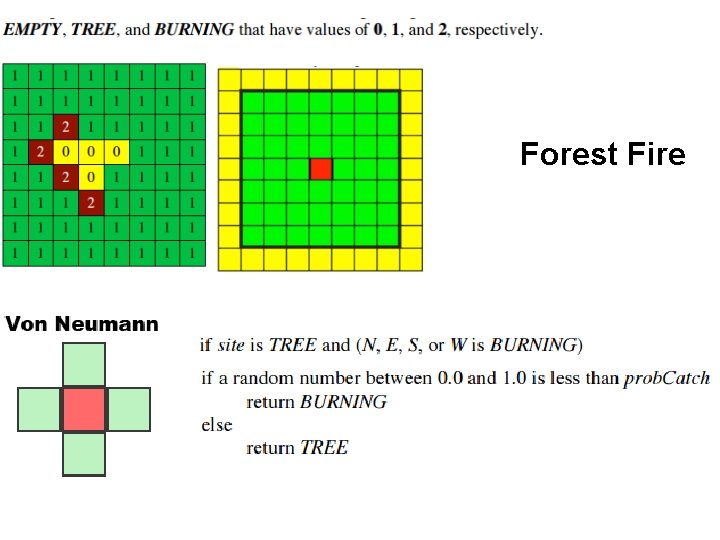
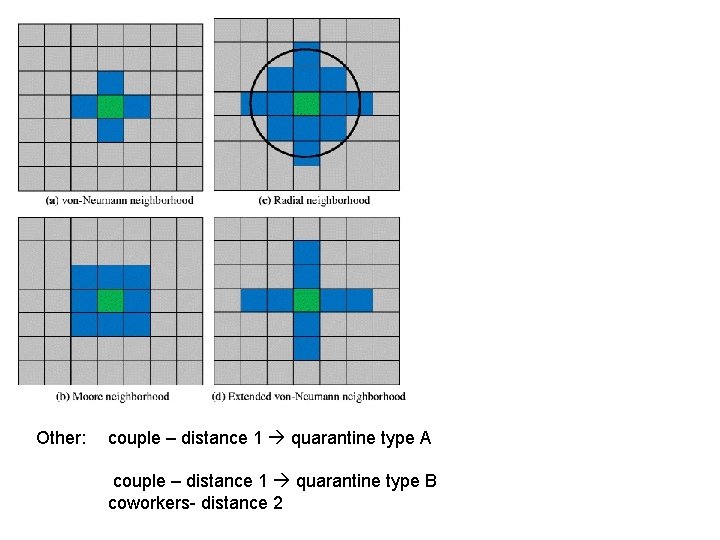
Moore Neighborhood Van Neumann Neighborhood Boundary conditions Right: Cells beyond the grid boundary Left: toroidal topology are always treated as if they were dead.



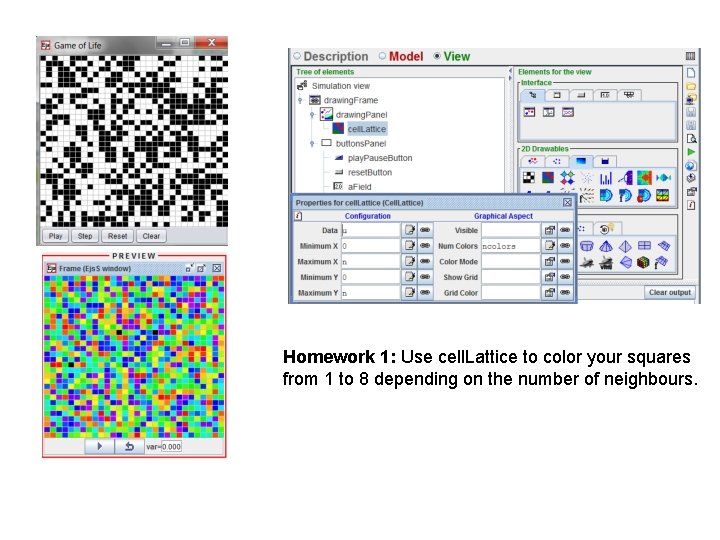
Homework 1: Use cell. Lattice to color your squares from 1 to 8 depending on the number of neighbours.

Homework 2: Find all 3 x 3 “creatures” (total number 2^18=262. 144 ) and find the number of creatures (up to vertical, horizontal, diagonal mirror symmetry): * Stable - Patterns that do not change over time * Oscillators - Patterns that change over time but repeat themselves every n cycles. * Flyers - Patterns that essentially stay the same over time but move across the board like a bird or spaceship. • Other patterns - Discover your own type of pattern Homework 3: Find the lifespans of 3 x 3 “creatures” classified to Other patterns. Find methuselahs with long lifespan Lifespan – number of generations until the pattern dies or becomes stable, oscillator or flyer. R-pentomimo with 1103 generations

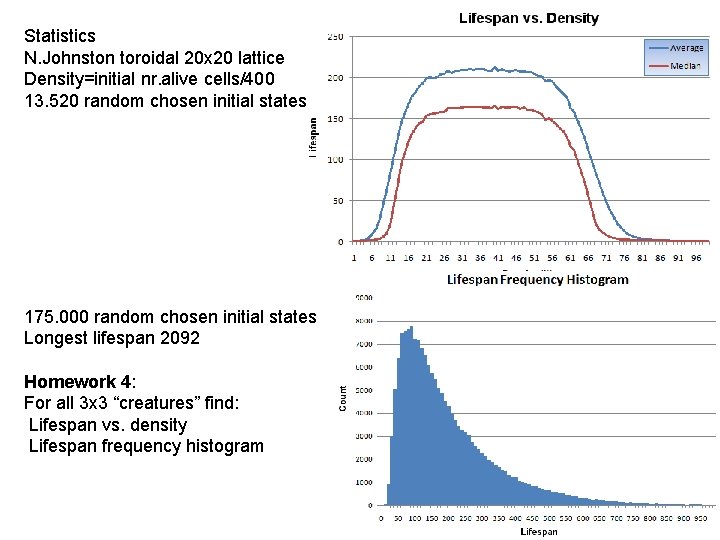
Statistics N. Johnston toroidal 20 x 20 lattice Density=initial nr. alive cells/400 13. 520 random chosen initial states 175. 000 random chosen initial states Longest lifespan 2092 Homework 4: For all 3 x 3 “creatures” find: Lifespan vs. density Lifespan frequency histogram

Homework 5: Explore other rules B 3/S 23 Conway Game of life – Born when 3 cells alive, Survive if two or three cells are alive B 36/S 23 – High Life B 2/S –Seeds B 23/S 3 –Reversed GOL B 02468/S 02468 – Evens B 3678/S 34678 – Day and night B 3/S 12345 – Maze B 45678/S 2345 – Walled cities

Forest Fire



Other: couple – distance 1 quarantine type A couple – distance 1 quarantine type B coworkers- distance 2


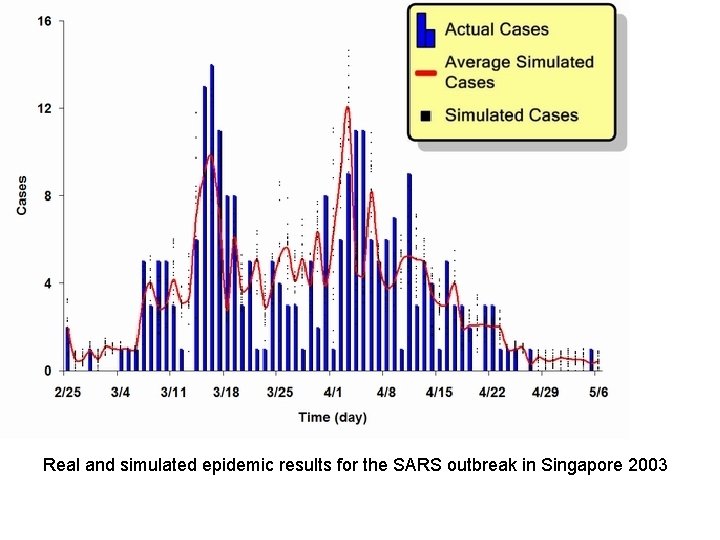
Real and simulated epidemic results for the SARS outbreak in Singapore 2003


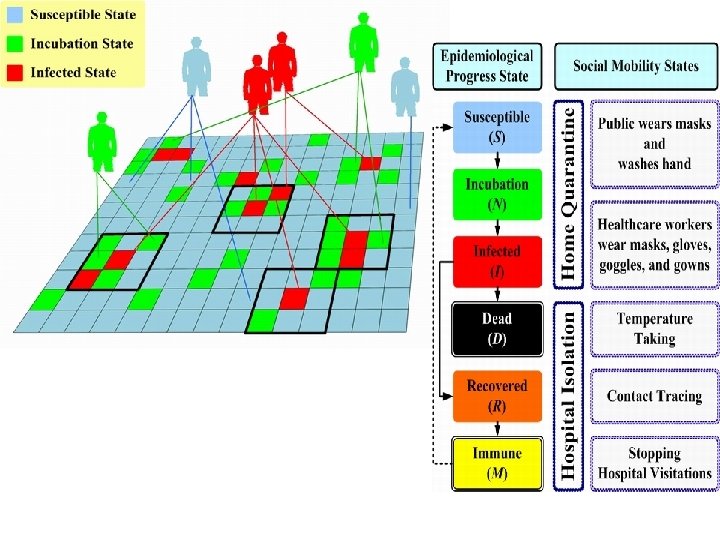
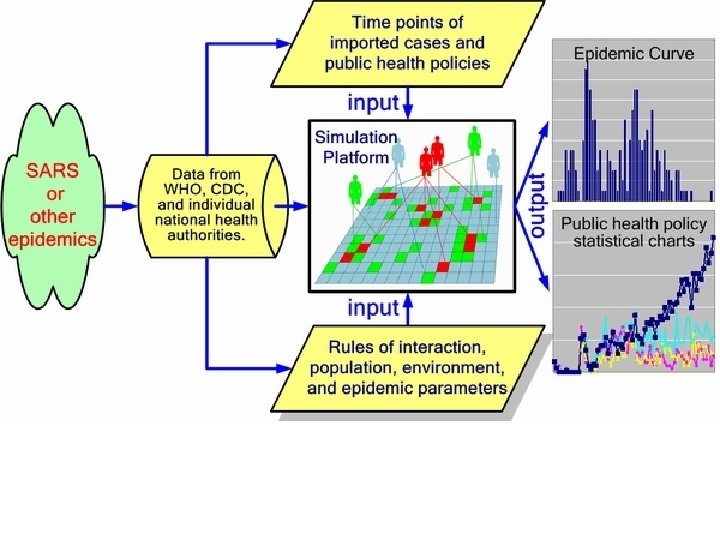
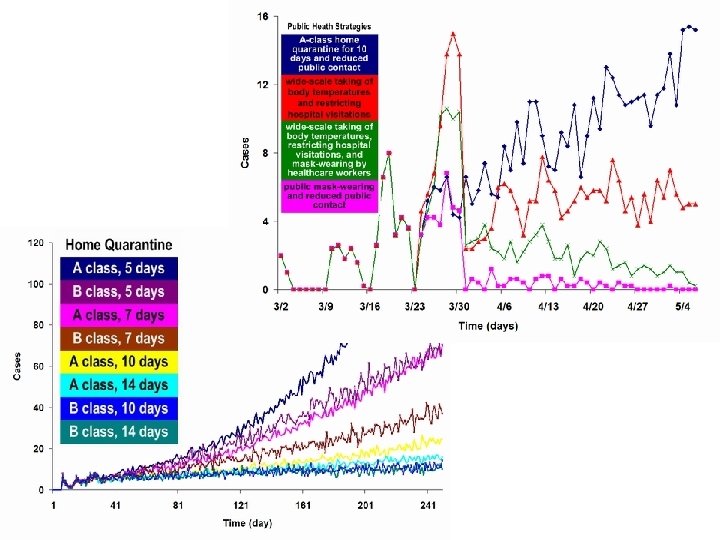
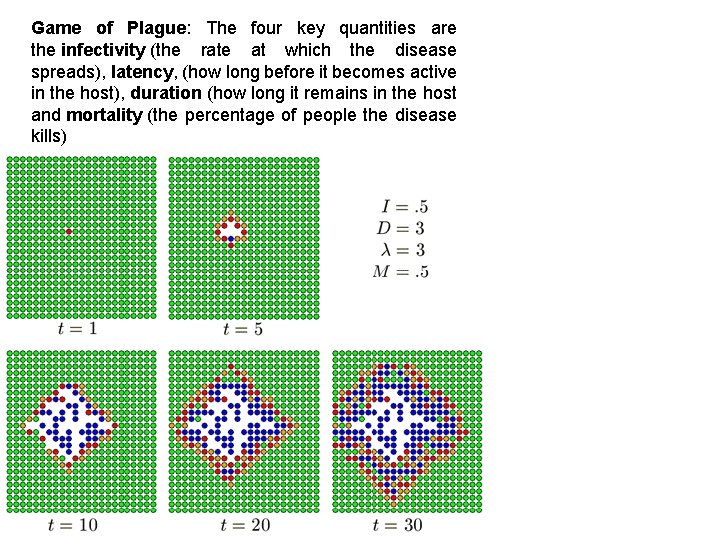
Game of Plague: The four key quantities are the infectivity (the rate at which the disease spreads), latency, (how long before it becomes active in the host), duration (how long it remains in the host and mortality (the percentage of people the disease kills)