Computational Methods in Astrophysics Dr Rob Thacker AT

Computational Methods in Astrophysics Dr Rob Thacker (AT 319 E) thacker@ap

Today’s Lecture Distributed Memory Computing II User defined (derived) datatypes, packing, communicators n Abstract topologies, Cartesian primitives, performance and scaling n

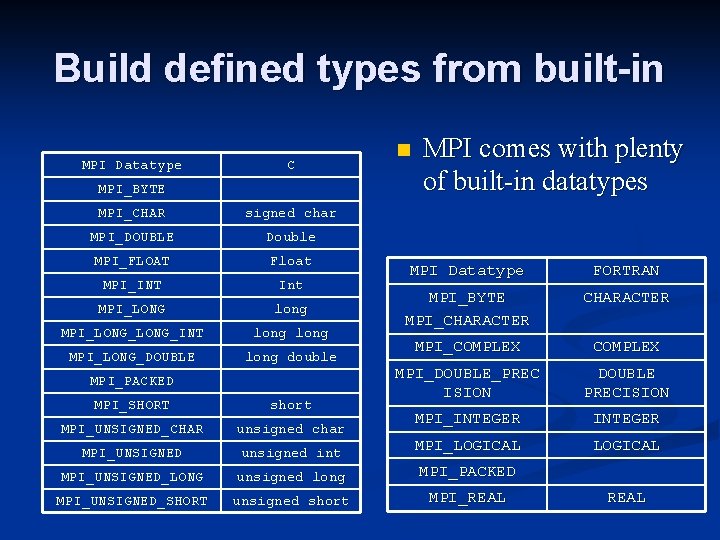
Build defined types from built-in MPI Datatype C MPI_BYTE MPI_CHAR signed char MPI_DOUBLE Double MPI_FLOAT Float MPI_INT Int MPI_LONG long MPI_LONG_INT long MPI_LONG_DOUBLE long double MPI_PACKED n MPI comes with plenty of built-in datatypes MPI Datatype FORTRAN MPI_BYTE MPI_CHARACTER MPI_COMPLEX MPI_DOUBLE_PREC ISION DOUBLE PRECISION MPI_INTEGER LOGICAL MPI_SHORT short MPI_UNSIGNED_CHAR unsigned char MPI_UNSIGNED unsigned int MPI_LOGICAL MPI_UNSIGNED_LONG unsigned long MPI_PACKED MPI_UNSIGNED_SHORT unsigned short MPI_REAL

Making a trivial new datatype n MPI_Type_contiguous(n, oldtype, newtype, ierror) n n Produces a new datatype that is n copies of the old Each entry is displaced by the extent of oldtype can be a derived datatype as well Must “commit” type before sending Use MPI_Type_commit(newtype, ierr) n Free up with MPI_Type_Free(newtype, ierr) – finite number of datatypes MPI_Send(buffer, count, datatype, dest, tag, comm, ierr) n Equivalent calls MPI_Type_contiguous(count, datatype, newtype, ierr) MPI_Type_commit(newtype, ierr) MPI_Send(buffer, 1, newtype, dest, tag, comm, ierr) MPI_Type_free(newtype, ierr)

Arbitrary datatypes n To derive a datatype from another n Specify a typemap of datatypes and BYTE displacements n The type signature is the list of basic datatypes within the new datatype: n Type signature directly controls the interpretation of both sent and received data, displacements indicate where to find information n Decodes information contained in the buffers

Vector datatypes n MPI_Type_vector(count, blocklength, stride, oldtype, newtype, ierror) n n The function selects count blocks of data of type oldtype Each block is blocklength data items long Separation between successive starting blocks is stride Function MPI_Type_contiguous can be thought of as a special case of MPI_Type_vector: n MPI_Type_contiguous(count, oldtype, newtype, ierr) = MPI_Type_vector(count, 1, 1, oldtype, newtype, ierr)

Vector Example n n Let oldtype = {(double, 0), (char, 8)} (named_double) Call MPI_Type_vector(2, 3, 4, named_double, six_named_doubles, ierr) n n New MPI data type, which has the following map: newtype = {(double, 0), (char, 8), (double, 16), (char, 24), (double, 32), (char, 40), (double, 64), (char, 72), (double, 80), (char, 88), (double, 96), (char, 104)} n n n Two blocks of data are taken, each containing 3 structures of the type named_double The 3 structures within the block are concatenated contiguously The stride is set to extent of 4 objects of the same type =

Indexed data types n MPI_Type_indexed(count, array_of_blocklengths, array_of_displacements, oldtype, newtype, ierror) n The function selects count blocks of data of type oldtype n Block n is array_of_blocklengths(n) data items long n List of displacements is defined relative to the first item n MPI_Type_vector can be thought of as a special case of MPI_Type_indexed All array_of_blocklengths entries = vector blocklen n List of displacements are multiples of the n

Example of using indexing n Suppose you only need a subset of an array Could send many short messages n Could pack a datatype n Better solution create a datatype the includes the displacements you need n Example: n 9 n 27 39 List of offsets: 9, 27, 39, 142

Example cont n n n In this case we have 4 elements (=n_to_move) Array of displacements (offset()) Each part of the list is a single element n n n `Block’ lengths are all unity (blocksize()) List datatype will be denoted ltype Following code performs the implicit packing for you: MPI_Type_indexed(n_to_move, blocksize, offset, ltype, newtype, ierr) MPI_Type_commit(newtype, ierr) MPI_Send(buffer, 1, newtype, dest, tag, comm, ierr) MPI_Type_free(newtype, ierr)

When to use H versions n Data maybe stored in dynamically allocated region n n No single buffer to refer displacements from MPI_Address(location, address, ierr) will return the byte address of the element location within an allocated window Create list of byte positions for Hindexed using MPI_Address MPI_BOTTOM can then be used as the starting address for the MPI_Send n MPI_Send(MPI_BOTTOM, 1, mytype, dest, tag, comm, ie rr)

Packing n On some occasions packing may be desirable over specifying a datatype n n e. g. packing across multiple arrays MPI_Pack allows a user to incrementally add data into a user provided buffer n MPI_Pack(inbuf, incount, datatype, outbuf, outcount, posi tion, comm, ierr) n n Packed data is given the MPI_PACKED datatype MPI_Pack_size can be used to determine how large the required buffer is in bytes n n Specify number of elements, MPI datatype, communicator Communicator is required since heterogeneous environment may require more packing than expected

Equivalent examples – both datatypes send the same message int I; char c[100]; MPI_Aint disp[2]; int blocklen[2] = {1, 100}; MPI_Datatype[2] = {MPI_INT, MPI_CHAR}; MPI_Datatype Type; /*create datatype*/ MPI_Get_address(&I, &(disp[0])); MPI_Get_address(c, &(disp[1])); MPI_Type_create_struct(2, blocklen, disp, type, &Type); MPI_Type_commit(&Type); Struct datatype /* Send */ MPI_Send(MPI_BOTTOM, 1, Type, 1, 0, MPI_COMM_WORLD); int I; char c[100]; char buffer[110]; int position = 0; Packed datatype /* Pack */ MPI_Pack(&i, 1, MPI_INT, buffer, 110, &position, MPI_COMM_WORLD); MPI_Pack(c, 100, MPI_CHAR, buffer, 110, &position, MPI_COMM_WORLD); /*send*/ MPI_Send(buffer, position, MPI_PACKED, 1, 0, MPI_COMM_WORLD);

Receiving & unpacking packed messages Note MPI_PACKED datatype can be used to receive any message n To unpack, make succesful calls to MPI_Unpack(inbuf, insize, position, outbuf, o utcount, datatype, comm, ierr) n First call starts at position 0 n Second call starts at the position returned by the first MPI_Unpack (value returned by position variable) n

MPI_Unpack example int I; char c[100]; MPI_Status status; char buffer[110]; int position = 0; /* receive */ MPI_Recv(buffer, 110, MPI_PACKED, 1, 0, MPI_COMM_WORLD, &status); /*unpack*/ MPI_Unpack(buffer, 110, &position, &i, 1, MPI_INT, MPI_COMM_WORLD); MPI_Unpack(buffer, 110, &position, c, 100, MPI_CHAR, MPI_COMM_WORLD);

Note on implementation n A packing unit may contain metadata (recall issue of heterogeneity in communicator) n n e. g. 64 processors of standard type, 1 additional graphics processor of opposite endian Any header will contain information on encoding and the size of the unit for error checking n n Implies you can’t concatenate two packed messages and send in a single operation Similarly can’t separate an incoming message into two sections and unpack separately

Topologies, Cartesian Primitives and messaging performance n n Applicable to applications where data structures reflect a specific domain decomposition Optional attribute that can be given to an intracommunicator only – not to intercommunicators May possibly help runtime mapping of processes onto hardware We’ll examine one code example that brings together a number of features we have discussed and places them in context

Inadequacies of linear ranking n Linear ranking implies a ring-like abstract topology for the processes n n n Few applications have a communication pattern that logically reflects a ring Two or three dimensional grids/torii are very common We define the logical processes arrangement defined by the communication pattern the “virtual topology” Do not confuse the virtual topology with the machine topology The virtual topology must be mapped to the hardware via an embedding This may or may not be beneficial

Graphs & Virtual Topologies n n Communication pattern defines a graph Communication graphs are assumed to be symmetric n n if a communicates with b, b can communicate with a Communicators allow messaging between any pair of nodes n virtual topologies may necessarily neglect some communication modes Cartesian example 0 1 2 3 (0, 2) (1, 2) (2, 2) (3, 2) 4 5 6 7 (0, 1) (1, 1) (2, 1) (3, 1) 8 9 10 11 (0, 0) (1, 0) (2, 0) (3, 0) 3 x 4 2 d virtual topology. Upper number is the rank, lower Value gives (column, row).

Specific example: Poisson Equation on 2 d grid interior boundary n n xi=i/n+1, where n defines number of points, same in y axis On unit square grid spacing h=1/n+1 Equation is approximated by Solve by guessing for u initially, then iteratively solve for u (Jacobi iteration) i, j+1 i, j i-1, j i+1, j i, j-1

2 d Poisson continued Rank=1 n n Calculation of the updated uk involves looping over all grid points How do we decompose the problem in parallel? n n n Rank=0 Simplest choice: 1 -d decomposition (slabs) Solid lines denote data stored on node Dotted lines denote all required data required for calculation n Nodes will always require data that they do not hold a copy of locally – ghost cells

Changes to the loop structure Single processor integer i, j, n double precision u(0: n+1, 0: n+1) double precision unew(0: n+1, 0: n+1) do j=1, n do i=1, n unew(i, j)= 0. 25*( u(i-1, j) + u(i, j+1)+u(i, j-1)+u(i+1, j) + -h**2*f(i, j)) end do n integer i, j, n double precision u(0: n+1, s-1: e+1) double precision unew(0: n+1, s-1: e+1) do j=s, e do i=1, n unew(i, j)= 0. 25*( u(i-1, j) + u(i, j+1)+u(i, j-1)+u(i+1, j) + -h**2*f(i, j)) end do Loop is now over node start and end points n n n Parallel Node Data arrays must include space for j+1 and j-1 entries in the y direction Ghost data must be communicated MPI_Cart topologies create the necessary facilities for this messaging to be done quickly and easily

MPI_Cart_create n n Creates a communicator with a Cartesian topology 2 nd through 5 th arguments define the new topology. 1 st argument is the initial communicator, 6 th argument is the new communicator n Example for a logical 2 d grid of processors: integer dims(2) logical isperiodic(2), reorder Dimensions of axes dims(1)=4 dims(2)=3 Are axis directions isperiodic(1)=. false. periodic? (consider grid isperiodic(2)=. false. on the Earth for example) reorder=. true. ndim=2 Rank in new communicator call MPI_Cart_create(MPI_COMM_WORLD, may be different from old + ndim, dims, isperiodic, reorder, (may improve performance) + comm 2 d, ierr)

Important issue n The topology MPI_Cart_create initializes is related to the communication required by the domain decomposition n Not the implicit communication structure of the algorithm For the 1 d decomposition all x values are contained on node – only y boundaries need be exhanged In the 2 d Poisson example we can choose either a 1 d or 2 d decomposition

Finding your coordinates & neighbours in the new communicator n MPI_Cart_get(comm 1 d, 1, dims, isperiodic, coords, ierr) n n n You may also want to convert a rank to coordinates n n Returns dims, isperiodic as defined in the communicator Calling processes coords are returned MPI_Cart_coords(comm 1 d, rank, maxdims, coords, ierr) If you call with your own rank then call returns your coords When moving data we frequently wish to move across one axis direction synchronously across all processors If you just want to send and receive ghost cell values to/from neighbours there is a simple mechanism for determining the neighbouring ranks n MPI_Cart_shift

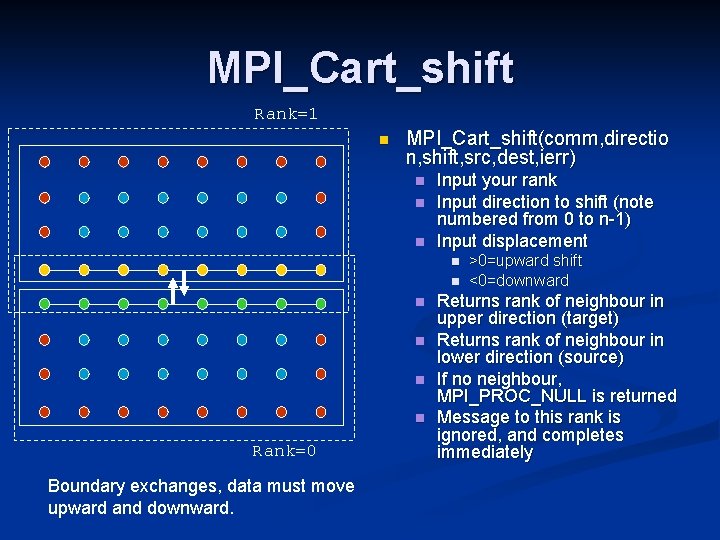
MPI_Cart_shift Rank=1 n MPI_Cart_shift(comm, directio n, shift, src, dest, ierr) n n n Input your rank Input direction to shift (note numbered from 0 to n-1) Input displacement n n n Rank=0 Boundary exchanges, data must move upward and downward. >0=upward shift <0=downward Returns rank of neighbour in upper direction (target) Returns rank of neighbour in lower direction (source) If no neighbour, MPI_PROC_NULL is returned Message to this rank is ignored, and completes immediately

Remaining ingredients n n n Still need to compute the start and end points for each node If n is divisible by nprocs (best for load balance): s = 1 + myrank * (n/nprocs) e = s + (n / nprocs) -1 When nprocs does not divide n naïve solution: s = 1 + myrank * (n/nprocs) if (myrank. eq. nprocs-1) then e = n else e = s + floor(n / nprocs) -1 end if n n Floor(x) returns largest integer value no greater than x Better to use MPE_Decomp 1 d to even out, but load balance still won’t be perfect (see the ANL/MSU MPI website)

http: //www-unix. mcs. anl. gov/mpi/usingmpi/examples/intermediate/oned_f. htm Prototype code call MPI_CART_CREATE( MPI_COMM_WORLD, 1, numprocs, . false. , . true. , comm 1 d, ierr ) $ c c Get my position in this communicator, and my neighbors c call MPI_COMM_RANK( comm 1 d, myid, ierr ) call MPI_Cart_shift( comm 1 d, 0, 1, nbrbottom, nbrtop, ierr ) c Compute the actual decomposition call MPE_DECOMP 1 D( ny, numprocs, myid, s, e ) c Initialize the right-hand-side (f) and the initial solution guess (a) call onedinit( a, b, f, nx, s, e ) c c Actually do the computation. Note the use of a collective operation to c check for convergence, and a do-loop to bound the number of iterations. c do 10 it=1, maxit call exchng 1( a, nx, s, e, comm 1 d, nbrbottom, nbrtop ) call sweep 1 d( a, f, nx, s, e, b ) ! Jacobi sweep call exchng 1( b, nx, s, e, comm 1 d, nbrbottom, nbrtop ) call sweep 1 d( b, f, nx, s, e, a ) dwork = diff( a, b, nx, s, e ) ! Convergence test call MPI_Allreduce( dwork, diffnorm, 1, MPI_DOUBLE_PRECISION, $ MPI_SUM, comm 1 d, ierr ) if (diffnorm. lt. 1. 0 e-5) goto 20 c if (myid. eq. 0) print *, 2*it, ' Difference is ', diffnorm 10 continue if (myid. eq. 0) print *, 'Failed to converge' 20 continue if (myid. eq. 0) then print *, 'Converged after ', 2*it, ' Iterations’ endif Routine alternately computes into a and then b – hen

Which routine determines performance (other than comp. kernel)? n n exchng 1 controls the messaging and how this is coded will strongly affect overall execution time Recall from last lecture, 5(!) different ways to do communication: n Blocking sends and receives n n Ordered send n n n match send and receive perfectly Sendrecv n n very bad idea, potentially unsafe (although in this case it is OK) systems deals with buffering Buffered Bsend Nonblocking Isend

Option #1: Simple sends and receives subroutine exchng 1( a, nx, s, e, comm 1 d, nbrbottom, nbrtop ) include 'mpif. h' integer nx, s, e double precision a(0: nx+1, s-1: e+1) integer comm 1 d, nbrbottom, nbrtop integer status(MPI_STATUS_SIZE), ierr C & & call MPI_SEND( a(1, e), nx, MPI_DOUBLE_PRECISION, nbrtop, 0, comm 1 d, ierr ) call MPI_RECV( a(1, s-1), nx, MPI_DOUBLE_PRECISION, nbrbottom, 0, comm 1 d, status, ierr ) call MPI_SEND( a(1, s), nx, MPI_DOUBLE_PRECISION, nbrbottom, 1, comm 1 d, ierr ) call MPI_RECV( a(1, e+1), nx, MPI_DOUBLE_PRECISION, nbrtop, 1, comm 1 d, status, ierr ) return end

Option #2: Matched sends and receives subroutine exchng 1( a, nx, s, e, comm 1 d, nbrbottom, nbrtop ) use mpi integer nx, s, e double precision a(0: nx+1, s-1: e+1) integer comm 1 d, nbrbottom, nbrtop, rank, coord integer status(MPI_STATUS_SIZE), ierr ! & & & & call MPI_COMM_RANK( comm 1 d, rank, ierr ) call MPI_CART_COORDS( comm 1 d, rank, 1, coord, ierr ) if (mod( coord, 2 ). eq. 0) then call MPI_SEND( a(1, e), nx, MPI_DOUBLE_PRECISION, nbrtop, 0, comm 1 d, ierr ) call MPI_RECV( a(1, s-1), nx, MPI_DOUBLE_PRECISION, nbrbottom, 0, comm 1 d, status, ierr ) call MPI_SEND( a(1, s), nx, MPI_DOUBLE_PRECISION, nbrbottom, 1, comm 1 d, ierr ) call MPI_RECV( a(1, e+1), nx, MPI_DOUBLE_PRECISION, nbrtop, 1, comm 1 d, status, ierr ) else call MPI_RECV( a(1, s-1), nx, MPI_DOUBLE_PRECISION, nbrbottom, 0, comm 1 d, status, ierr ) call MPI_SEND( a(1, e), nx, MPI_DOUBLE_PRECISION, nbrtop, 0, comm 1 d, ierr ) call MPI_RECV( a(1, e+1), nx, MPI_DOUBLE_PRECISION, nbrtop, 1, comm 1 d, status, ierr ) call MPI_SEND( a(1, s), nx, MPI_DOUBLE_PRECISION, nbrbottom, 1, comm 1 d, ierr ) endif return end

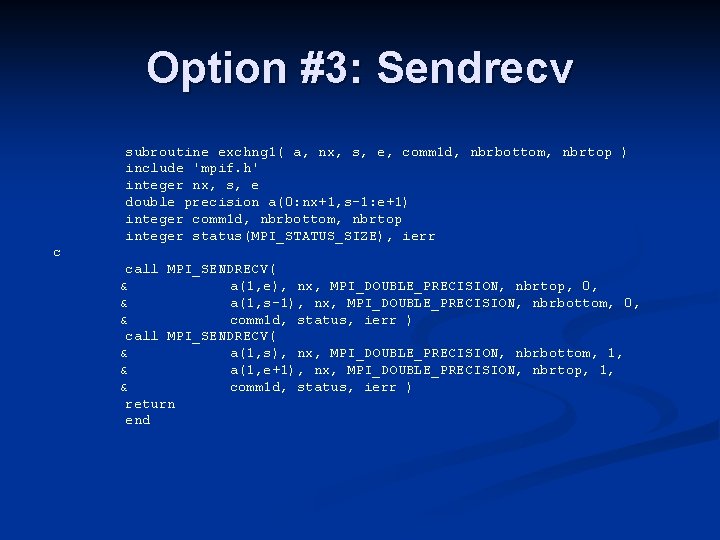
Option #3: Sendrecv subroutine exchng 1( a, nx, s, e, comm 1 d, nbrbottom, nbrtop ) include 'mpif. h' integer nx, s, e double precision a(0: nx+1, s-1: e+1) integer comm 1 d, nbrbottom, nbrtop integer status(MPI_STATUS_SIZE), ierr c call MPI_SENDRECV( & a(1, e), nx, MPI_DOUBLE_PRECISION, nbrtop, 0, & a(1, s-1), nx, MPI_DOUBLE_PRECISION, nbrbottom, 0, & comm 1 d, status, ierr ) call MPI_SENDRECV( & a(1, s), nx, MPI_DOUBLE_PRECISION, nbrbottom, 1, & a(1, e+1), nx, MPI_DOUBLE_PRECISION, nbrtop, 1, & comm 1 d, status, ierr ) return end

Option #4: Buffered Bsend subroutine exchng 1( a, nx, s, e, comm 1 d, nbrbottom, nbrtop ) use mpi integer nx, s, e double precision a(0: nx+1, s-1: e+1) integer comm 1 d, nbrbottom, nbrtop integer status(MPI_STATUS_SIZE), ierr call MPI_BSEND( a(1, e), nx, MPI_DOUBLE_PRECISION, nbrtop, & 0, comm 1 d, ierr ) call MPI_RECV( a(1, s-1), nx, MPI_DOUBLE_PRECISION, nbrbottom, & 0, comm 1 d, status, ierr ) call MPI_BSEND( a(1, s), nx, MPI_DOUBLE_PRECISION, nbrbottom, & 1, comm 1 d, ierr ) call MPI_RECV( a(1, e+1), nx, MPI_DOUBLE_PRECISION, nbrtop, & 1, comm 1 d, status, ierr ) return end Must also provide buffer space and connected to it via MPI_BUFFER_ATTACH (see Using MPI book)

Option #5: Nonblocking Isend subroutine exchng 1( a, nx, s, e, comm 1 d, nbrbottom, nbrtop ) include 'mpif. h' integer nx, s, e double precision a(0: nx+1, s-1: e+1) integer comm 1 d, nbrbottom, nbrtop integer status_array(MPI_STATUS_SIZE, 4), ierr, req(4) C call MPI_IRECV ( & a(1, s-1), nx, MPI_DOUBLE_PRECISION, nbrbottom, 0, & comm 1 d, req(1), ierr ) call MPI_IRECV ( & a(1, e+1), nx, MPI_DOUBLE_PRECISION, nbrtop, 1, & comm 1 d, req(2), ierr ) call MPI_ISEND ( & a(1, e), nx, MPI_DOUBLE_PRECISION, nbrtop, 0, & comm 1 d, req(3), ierr ) call MPI_ISEND ( & a(1, s), nx, MPI_DOUBLE_PRECISION, nbrbottom, 1, & comm 1 d, req(4), ierr ) C call MPI_WAITALL ( 4, req, status_array, ierr ) return end

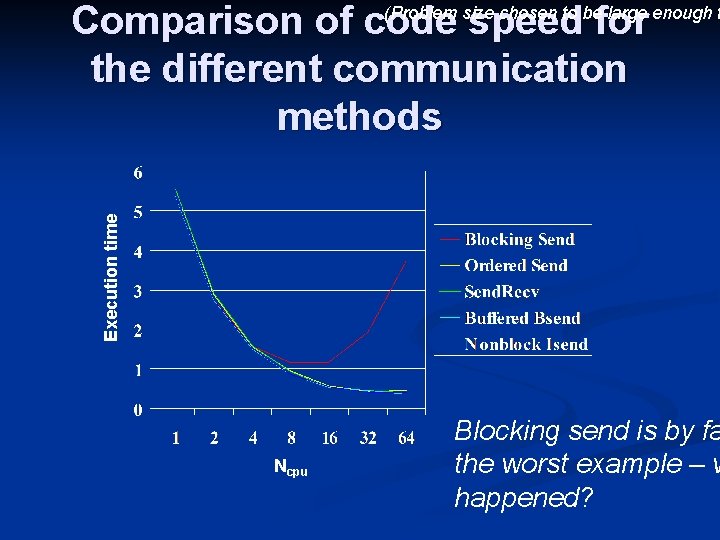
Comparison of code speed for the different communication methods Execution time (Problem size chosen to be large enough t Ncpu Blocking send is by fa the worst example – w happened?

What happens in the blocking sending version? n n The blocking communication can create a serial cascade “Top process” sends a message to a null process which completes It can then receive from another process P 5 P 0 P 2 P 3 P 4 n The ability. P 1 to receive then cascades through the SEND SEND RECV process ranks n RECV Completely serial communication Time RECV

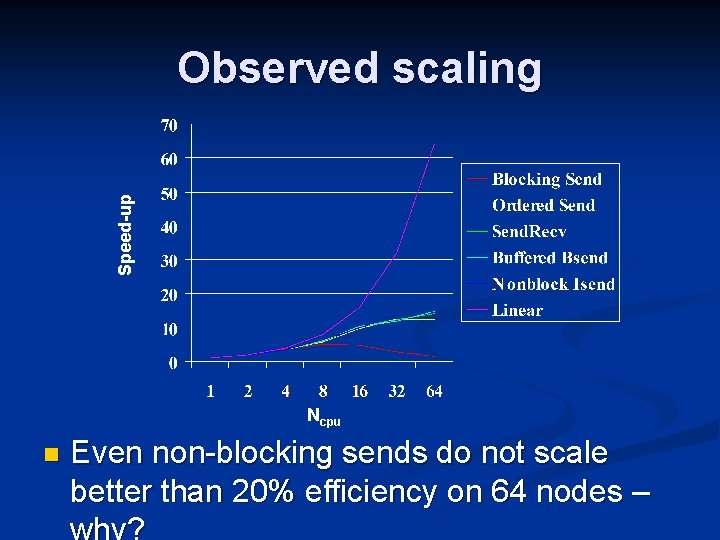
Speed-up Observed scaling Ncpu n Even non-blocking sends do not scale better than 20% efficiency on 64 nodes –

Scalability Analysis n n Examine execution time to see if time in communication is a bottleneck Time to send n bytes: Timecomm=s+r*n n Time in exchng 1 d routine ~ 2(s+r*n) n n s = start-up overhead r = time to send one byte (~1/bandwidth) n=8*nx for double precision data Communication time per process is fixed regardless of number of processors! n Communication doesn’t scale

2 -d topology communication time n Excluding processors on domain edge, then exchange of x boundary, followed by exchange of y boundary n For a square, with p total processors n Communication time decreases as a function of 1/sqrt(p) – moderately scalable Note for a small number of processors 1 d decomposition is actually better n

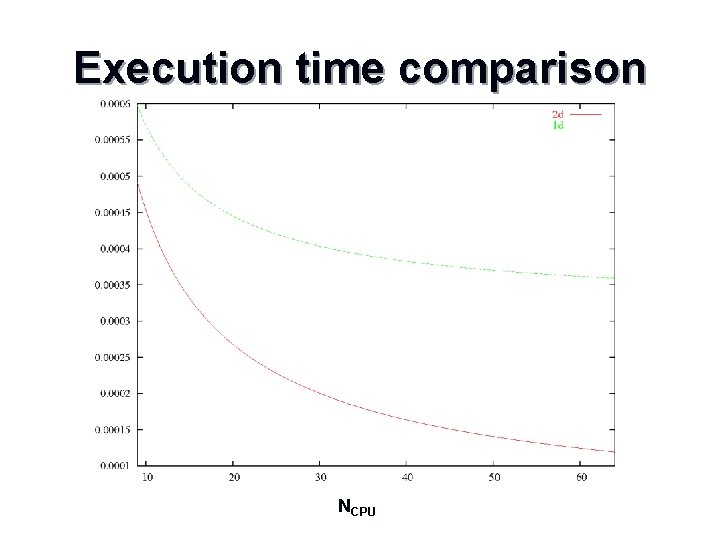
Execution time comparison NCPU

Changes required for the 2 -d domain decomposition n Need to update process topology n n Need two calls to MPI_Cart_shift n n n One for each axis direction Body of sweep routine must change loop limits n n MPI_Cart_create(MPI_COMM_WORLD, 2, . . Now have limits in x direction Arrays must also be updated for smaller sizes Lastly, exchng 1 must be updated to exchng 2 n Boundary exchanges in both directions

2 d: User derived datatype for boundary exchanges n x-boundary consists of non-contiguous memory locations n n Unavoidable due to 2 d array being mapped into memory Use MPI_Type_vector discussed previously 57 58 59 60 61 62 63 64 49 50 51 52 53 54 55 56 41 42 43 44 45 46 47 48 33 34 35 36 37 38 39 40 25 26 27 28 29 30 31 32 17 18 19 20 21 22 23 24 9 1 10 11 12 13 14 15 16 2 3 4 5 6 7 8

Solution n Number of blocks = (y end)-(y start)+1=ey-sy+3 n n n 1 entry per block Stride = (x end)-(x start)+1 = ex-sx+3 n n e. g. if end=4, start=2 there are 3 entries Remember it is a displacement between entries Create and commit: call MPI_Type_vector(ey-sy+3, 1, ex-sx+3, & MPI_DOUBLE_PRECISION, stridetype, ierr) call MPI_Type_commit(stridetype, ierr)

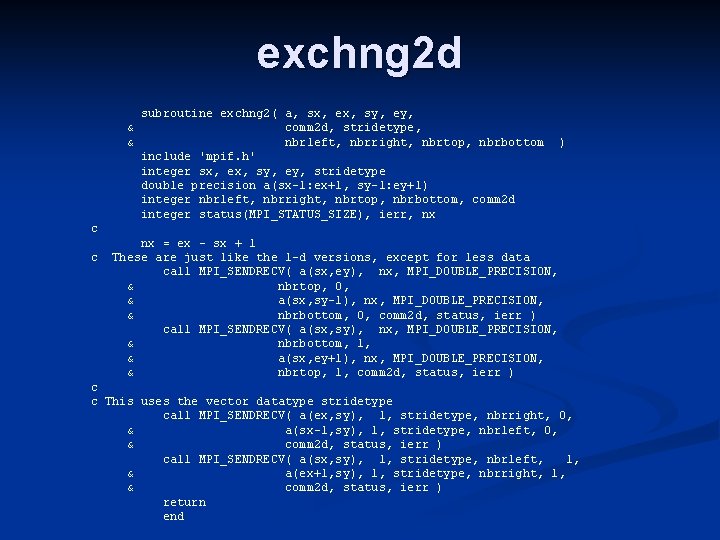
exchng 2 d & & subroutine exchng 2( a, sx, ex, sy, ey, comm 2 d, stridetype, nbrleft, nbrright, nbrtop, nbrbottom include 'mpif. h' integer sx, ex, sy, ey, stridetype double precision a(sx-1: ex+1, sy-1: ey+1) integer nbrleft, nbrright, nbrtop, nbrbottom, comm 2 d integer status(MPI_STATUS_SIZE), ierr, nx ) c c nx = ex - sx + 1 These are just like the 1 -d versions, except for less data call MPI_SENDRECV( a(sx, ey), nx, MPI_DOUBLE_PRECISION, & nbrtop, 0, & a(sx, sy-1), nx, MPI_DOUBLE_PRECISION, & nbrbottom, 0, comm 2 d, status, ierr ) call MPI_SENDRECV( a(sx, sy), nx, MPI_DOUBLE_PRECISION, & nbrbottom, 1, & a(sx, ey+1), nx, MPI_DOUBLE_PRECISION, & nbrtop, 1, comm 2 d, status, ierr ) c c This uses the vector datatype stridetype call MPI_SENDRECV( a(ex, sy), 1, stridetype, nbrright, 0, & a(sx-1, sy), 1, stridetype, nbrleft, 0, & comm 2 d, status, ierr ) call MPI_SENDRECV( a(sx, sy), 1, stridetype, nbrleft, 1, & a(ex+1, sy), 1, stridetype, nbrright, 1, & comm 2 d, status, ierr ) return end

Overlapping communication and computation n The expensive nature of communication argues for overlapping (pipelining!) it with computation n n Increasing divide between CPU speed and message latency means this will only be more important in the future Not always achievable – e. g. master-slave task decomposition Nonblocking communication facilitates this kind of overlap 2 d Poisson example n Interior of arrays can be calculated without the ghost cells

Computation that can be computed without ghost cells n n n All blue points are contained on node Red points denote ghost cells Blue points contained within the rectangle use only local data 2 d domain decomposition

Steps in comms/comp overlapping version 1. 2. 3. 4. 5. Indicate where data from other processes is to be received Post non-blocking sends to other processes Perform local computation Check for arrival of data from other processes Final algorithm is more complicated than the non-overlappi Complete remaining computation version, but all the necessary code has already been writte algorithmic structure is used universally to overlap comms

Structure of computation of final pieces n n Post 4 MPI_Irecv’s and 4 MPI_Isends Handles from the 4 Irecv’s determine which part of the remaining cells to compute Use MPI_WAITANY to test on whether operations have completed Ignore completion of sends (but must still ensure they have completed) do 100 k=1, 8 call MPI_WAITANY( 8, requests, idx, status, ierr ) ! Use tag to determine which edge if (idx. eq. 1) then do j=sy, ey ! Left hand cells unew(si, j) =. . . end do else if (idx. eq. 2) then do j=sy, ey ! Right hand cells unew(ei, j) =. . . end do else if (idx. eq. 3) then do i=sx, ex ! Upper cells unew(i, ej) =. . . end do else if (idx. eq. 4) then do i=sx, ex ! Lower cells unew(i, sj) =. . . end do end if end do

Note about overlapping comms and comps n n Nonblocking operations were introduced first and foremost to allow the writing of safe programs Many implementations cannot physically overlap without additional hardware n n n Communication processor or system communication thread Thus nonblocking operations may allow the overlapping, but they are not required to If code that overlaps comms/comps does not increase performance it may not be your fault

3 d n n n Problem sizes scale cubically in three dimensions Number of grids cells frequently exceeds 107 Large amount of work makes 3 d codes natural candidates for parallelization Domain decomposition is expected to best for a 3 d virtual topology MPI_Dims_create(nodes, ndims, dims) divides up nodes into best load balanced topology n n n e. g. MPI_Dims_create(6, 3, dims) gives dims=(3, 2, 1) Values of dims may be set before the call, e. g. dims=(0, 3, 0) then MPI_Dims_create(6, 3, dims) gives dims=(2, 3, 1) If nodes is not divisible then an error is returned

Summary Domain decomposition determines the communication pattern required n The topology primitives provide a fast and simple way to write the communication routines n The decomposition and communication pattern will frequently determine the scalability of a code n Overlapping comms and comps is a good idea, but is not always achievable n