Computational Intelligence Winter Term 201415 Prof Dr Gnter

Computational Intelligence Winter Term 2014/15 Prof. Dr. Günter Rudolph Lehrstuhl für Algorithm Engineering (LS 11) Fakultät für Informatik TU Dortmund

Plan for Today Lecture 02 ● Single-Layer Perceptron § Accelerated Learning § Online- vs. Batch-Learning ● Multi-Layer-Perceptron § Model § Backpropagation G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 2

Single-Layer Perceptron (SLP) Lecture 02 Acceleration of Perceptron Learning Assumption: x 2 { 0, 1 }n ) ||x|| ≥ 1 for all x ≠ (0, . . . , 0)‘ If classification incorrect, then w‘x < 0. Consequently, size of error is just = -w‘x > 0. ) wt+1 = wt + ( + ) x w‘t+1 x for > 0 (small) corrects error in a single step, since = (wt + ( + ) x)‘ x = w‘t x + ( + ) x‘x = - + ||x||2 = (||x||2 – 1) + ||x||2 > 0 ≥ 0 >0 G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 3

Single-Layer Perceptron (SLP) Lecture 02 Generalization: Assumption: x 2 Rn ) ||x|| > 0 for all x ≠ (0, . . . , 0)‘ as before: wt+1 = wt + ( + ) x for > 0 (small) and = - w‘t x > 0 ) w‘t+1 x = (||x||2 – 1) + ||x||2 < 0 possible! > 0 Idea: Scaling of data does not alter classification task! Let Set = min { || x || : x 2 B } > 0 ^x = x ^ ) set of scaled examples B ) || ^x || ≥ 1 ) || ^x ||2 – 1 ≥ 0 ) w’t+1 ^x > 0 G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 4

Single-Layer Perceptron (SLP) Lecture 02 There exist numerous variants of Perceptron Learning Methods. Theorem: (Duda & Hart 1973) If rule for correcting weights is wt+1 = wt + t x (if w‘t x < 0) 1. 8 t ≥ 0 : t ≥ 0 2. 3. then wt → w* for t → 1 with 8 x‘w* > 0. e. g. : t = > 0 or ■ t = / (t+1) for > 0 G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 5

Single-Layer Perceptron (SLP) Lecture 02 as yet: Online Learning → Update of weights after each training pattern (if necessary) now: Batch Learning → Update of weights only after test of all training patterns → Update rule: wt+1 = wt + x ( > 0) w‘t x < 0 x 2 B vague assessment in literature: • advantage : „usually faster“ • disadvantage : „needs more memory“ just a single vector! G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 6

Single-Layer Perceptron (SLP) Lecture 02 find weights by means of optimization Let F(w) = { x 2 B : w‘x < 0 } be the set of patterns incorrectly classified by weight w. Objective function: f(w) = – w‘x → min! x 2 F(w) Optimum: f(w) = 0 iff F(w) is empty Possible approach: gradient method wt+1 = wt – rf(wt) ( > 0) converges to a local minimum (dep. on w 0) G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 7

Single-Layer Perceptron (SLP) Lecture 02 Gradient method wt+1 = wt – rf(wt) Gradient points in direction of steepest ascent of function f(¢) Caution: Indices i of wi here denote components of vector w; they are not the iteration counters! G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 8

Single-Layer Perceptron (SLP) Lecture 02 Gradient method thus: gradient method batch learning G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 9

Single-Layer Perceptron (SLP) Lecture 02 How difficult is it (a) to find a separating hyperplane, provided it exists? (b) to decide, that there is no separating hyperplane? Let B = P [ { -x : x 2 N } (only positive examples), wi 2 R, 2 R , |B| = m For every example xi 2 B should hold: xi 1 w 1 + xi 2 w 2 +. . . + xin wn ≥ → trivial solution wi = = 0 to be excluded! Therefore additionally: 2 R xi 1 w 1 + xi 2 w 2 +. . . + xin wn – – ≥ 0 Idea: maximize → if * > 0, then solution found G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 10

Single-Layer Perceptron (SLP) Lecture 02 Matrix notation: Linear Programming Problem: f(z 1, z 2, . . . , zn+1, zn+2) = zn+2 → max! s. t. calculated by e. g. Kamarkaralgorithm in polynomial time Az ≥ 0 If zn+2 = > 0, then weights and threshold are given by z. Otherwise separating hyperplane does not exist! G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 11

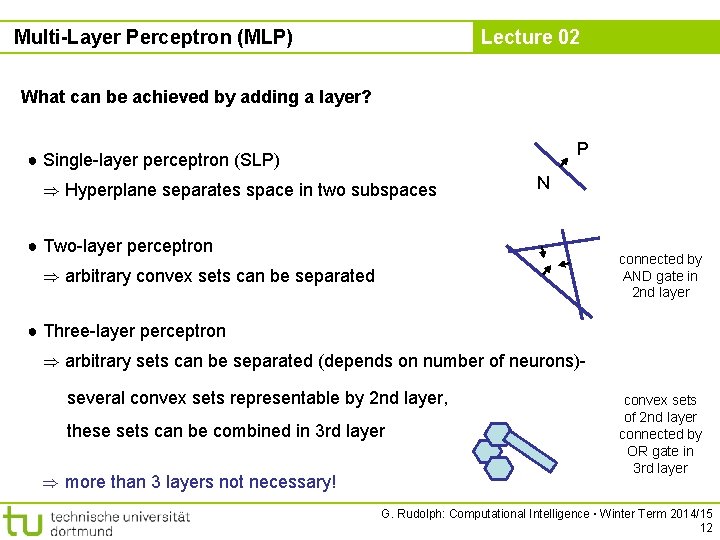
Multi-Layer Perceptron (MLP) Lecture 02 What can be achieved by adding a layer? P ● Single-layer perceptron (SLP) ) Hyperplane separates space in two subspaces N ● Two-layer perceptron connected by AND gate in 2 nd layer ) arbitrary convex sets can be separated ● Three-layer perceptron ) arbitrary sets can be separated (depends on number of neurons)several convex sets representable by 2 nd layer, these sets can be combined in 3 rd layer ) more than 3 layers not necessary! convex sets of 2 nd layer connected by OR gate in 3 rd layer G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 12

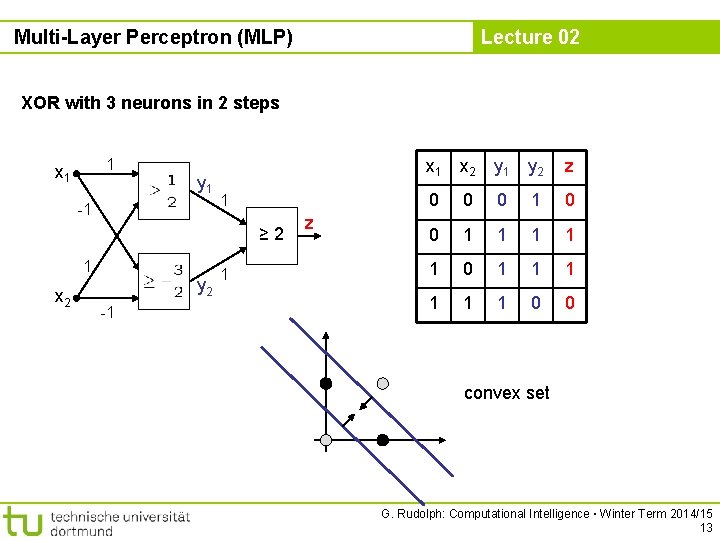
Multi-Layer Perceptron (MLP) Lecture 02 XOR with 3 neurons in 2 steps 1 x 1 y 1 -1 1 ≥ 2 1 x 2 y 2 -1 1 z x 1 x 2 y 1 y 2 z 0 0 0 1 1 1 0 0 convex set G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 13

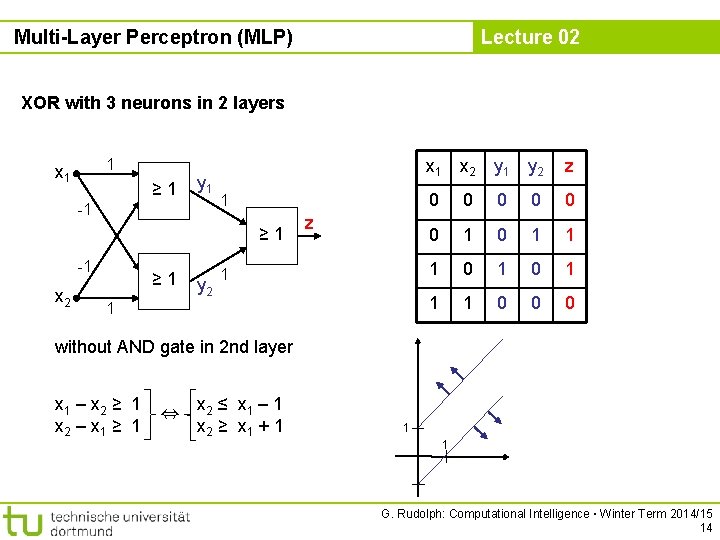
Multi-Layer Perceptron (MLP) Lecture 02 XOR with 3 neurons in 2 layers 1 x 1 ≥ 1 y 1 -1 1 ≥ 1 -1 x 2 ≥ 1 y 2 z 1 1 x 2 y 1 y 2 z 0 0 0 1 0 1 1 1 0 0 0 without AND gate in 2 nd layer x 1 – x 2 ≥ 1 x 2 – x 1 ≥ 1 , x 2 ≤ x 1 – 1 x 2 ≥ x 1 + 1 1 1 G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 14

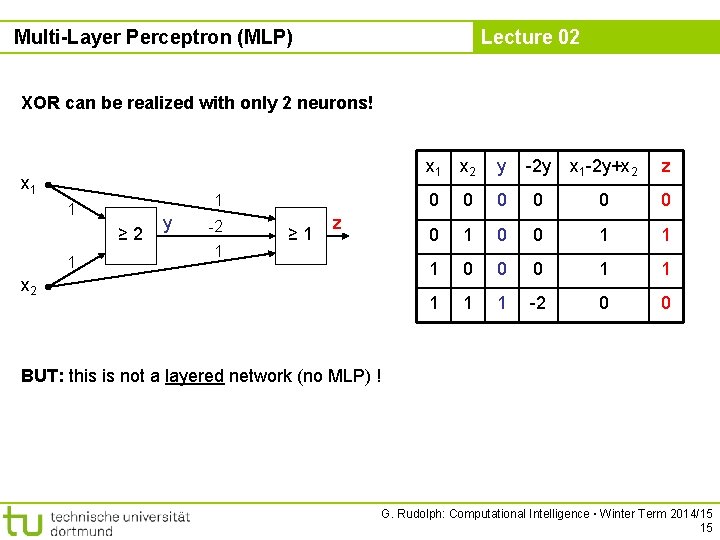
Multi-Layer Perceptron (MLP) Lecture 02 XOR can be realized with only 2 neurons! x 1 1 1 ≥ 2 1 y -2 1 ≥ 1 z x 2 x 1 x 2 y -2 y x 1 -2 y+x 2 z 0 0 0 0 1 1 1 0 0 0 1 1 1 -2 0 0 BUT: this is not a layered network (no MLP) ! G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 15

Multi-Layer Perceptron (MLP) Lecture 02 Evidently: MLPs deployable for addressing significantly more difficult problems than SLPs! But: How can we adjust all these weights and thresholds? Is there an efficient learning algorithm for MLPs? History: Unavailability of efficient learning algorithm for MLPs was a brake shoe. . . until Rumelhart, Hinton and Williams (1986): Backpropagation Actually proposed by Werbos (1974). . . but unknown to ANN researchers (was Ph. D thesis) G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 16

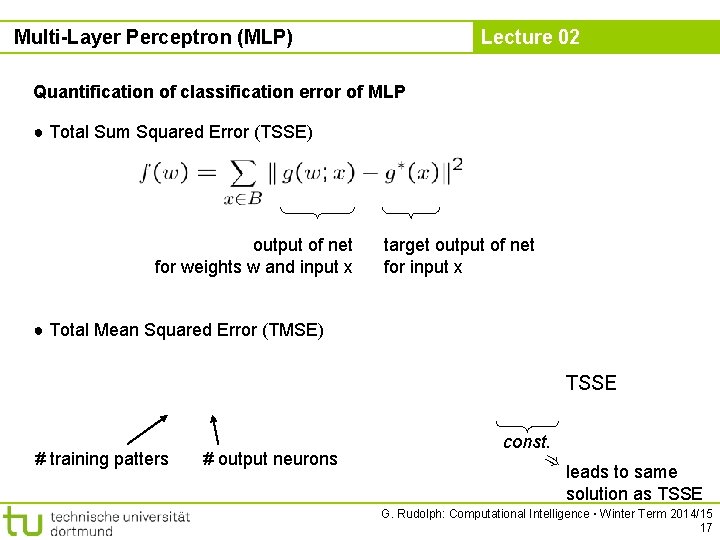
Multi-Layer Perceptron (MLP) Lecture 02 Quantification of classification error of MLP ● Total Sum Squared Error (TSSE) output of net for weights w and input x target output of net for input x ● Total Mean Squared Error (TMSE) TSSE # training patters # output neurons const. ) leads to same solution as TSSE G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 17

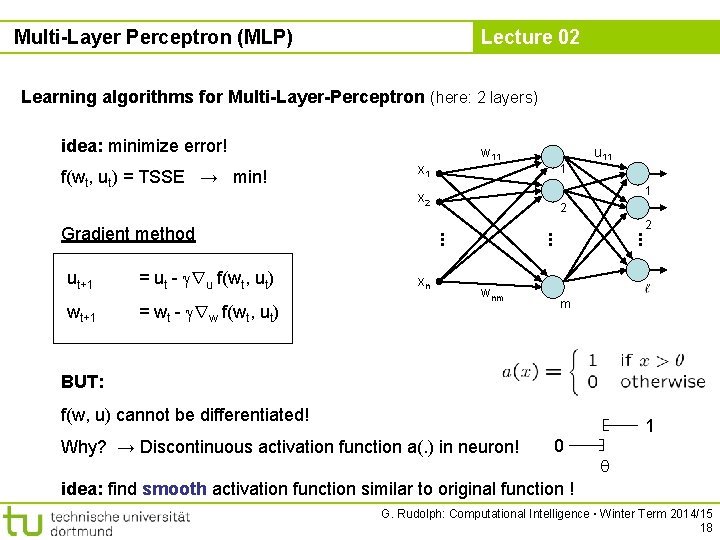
Multi-Layer Perceptron (MLP) Lecture 02 Learning algorithms for Multi-Layer-Perceptron (here: 2 layers) idea: minimize error! f(wt, ut) = TSSE → min! x 1 2 wnm . . . = wt - rw f(wt, ut) xn . . . wt+1 2 . . . = ut - ru f(wt, ut) 1 u 11 1 x 2 Gradient method ut+1 w 11 m BUT: f(w, u) cannot be differentiated! Why? → Discontinuous activation function a(. ) in neuron! 0 1 idea: find smooth activation function similar to original function ! G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 18

Multi-Layer Perceptron (MLP) Lecture 02 Learning algorithms for Multi-Layer-Perceptron (here: 2 layers) good idea: sigmoid activation function (instead of signum function) 0 1 1 • monotone increasing 0 • differentiable • non-linear • output 2 [0, 1] instead of 2 { 0, 1 } e. g. : ● ● • threshold integrated in activation function values of derivatives directly determinable from function values G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 19

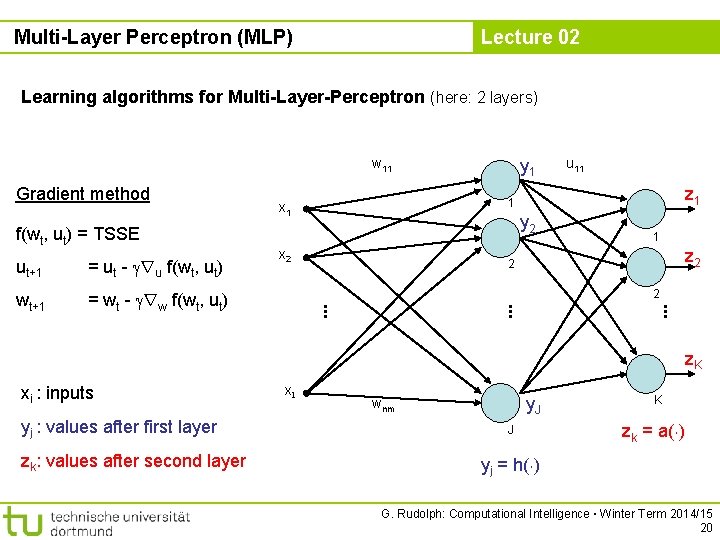
Multi-Layer Perceptron (MLP) Lecture 02 Learning algorithms for Multi-Layer-Perceptron (here: 2 layers) w 11 Gradient method f(wt, ut) = TSSE = wt - rw f(wt, ut) y 2 x 2 1 z 2 2 2 . . . wt+1 z 1 . . . = ut - ru f(wt, ut) u 11 1 x 1 . . . ut+1 y 1 z. K xi : inputs yj : values after first layer zk: values after second layer x. I y. J wnm J K zk = a(¢) yj = h(¢) G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 20

Multi-Layer Perceptron (MLP) Lecture 02 output of neuron j after 1 st layer output of neuron k after 2 nd layer error of input x: output of net target output for input x G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 21

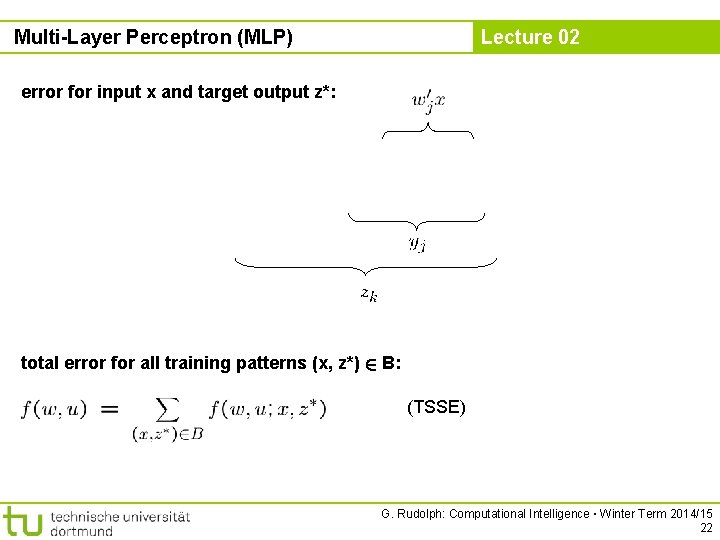
Multi-Layer Perceptron (MLP) Lecture 02 error for input x and target output z*: total error for all training patterns (x, z*) 2 B: (TSSE) G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 22

Multi-Layer Perceptron (MLP) Lecture 02 gradient of total error: vector of partial derivatives w. r. t. weights ujk and wij thus: and G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 23

Multi-Layer Perceptron (MLP) assume: Lecture 02 ) and: chain rule of differential calculus: outer derivative inner derivative G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 24

Multi-Layer Perceptron (MLP) Lecture 02 partial derivative w. r. t. ujk: “error signal“ k G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 25

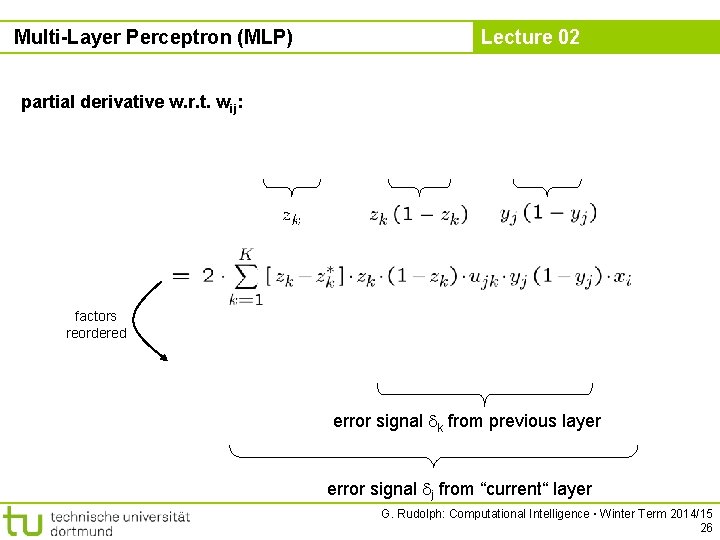
Multi-Layer Perceptron (MLP) Lecture 02 partial derivative w. r. t. wij: factors reordered error signal k from previous layer error signal j from “current“ layer G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 26

Multi-Layer Perceptron (MLP) Lecture 02 Generalization (> 2 layers) Let neural network have L layers S 1, S 2, . . . SL. Let neurons of all layers be numbered from 1 to N. j 2 Sm → neuron j is in m -th layer All weights wij are gathered in weights matrix W. Let oj be output of neuron j. error signal: correction: in case of online learning: correction after each test pattern presented G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 27

Multi-Layer Perceptron (MLP) Lecture 02 error signal of neuron in inner layer determined by ● error signals of all neurons of subsequent layer and ● weights of associated connections. ) ● First determine error signals of output neurons, ● use these error signals to calculate the error signals of the preceding layer, ● and so forth until reaching the first inner layer. ) thus, error is propagated backwards from output layer to first inner ) backpropagation (of error) G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 28

Multi-Layer Perceptron (MLP) Lecture 02 ) other optimization algorithms deployable! in addition to backpropagation (gradient descent) also: ● Backpropagation with Momentum take into account also previous change of weights: ● Quick. Prop assumption: error function can be approximated locally by quadratic function, update rule uses last two weights at step t – 1 and t – 2. ● Resilient Propagation (RPROP) exploits sign of partial derivatives: 2 times negative or positive ) increase step! change of sign ) reset last step and decrease step! typical values: factor for decreasing 0, 5 / factor of increasing 1, 2 ● evolutionary algorithms individual = weights matrix later more about this! G. Rudolph: Computational Intelligence ▪ Winter Term 2014/15 29