Computational Geometry Some useful algorithmsformulas for solving geometric

Computational Geometry Some useful algorithms/formulas for solving geometric problems

Overview n n n Representation Basic geometric problems Other issues

Representation n Points n n n Segments n n Position of the end points Lines n n (x, y) Cartesian coordinates (r, Θ) Polar coordinates 2 -tuple (m, c) using y = mx + c 3 -tuple (a, b, c) using ax + by = c Two points P 0, P 1 on the line using P(t) = (1 -t)P 0 + t P 1 Polygon n Ordered list of points

Basic geometric problems n n n n Area of polygon CCW Line segment intersection Distance between a point and a line Closest point Angle between two lines Point in a polygon Convex hull

Area of polygon n Given a simple polygon, find its area. (x 2, y 2) … (x 1, y 1) (xn, yn) n Area = 1/2 * [(x 1. y 2 + x 2. y 3 +…+ xn. y 1) - (y 1. x 2 + y 2. x 3 + … + yn, x 1)]

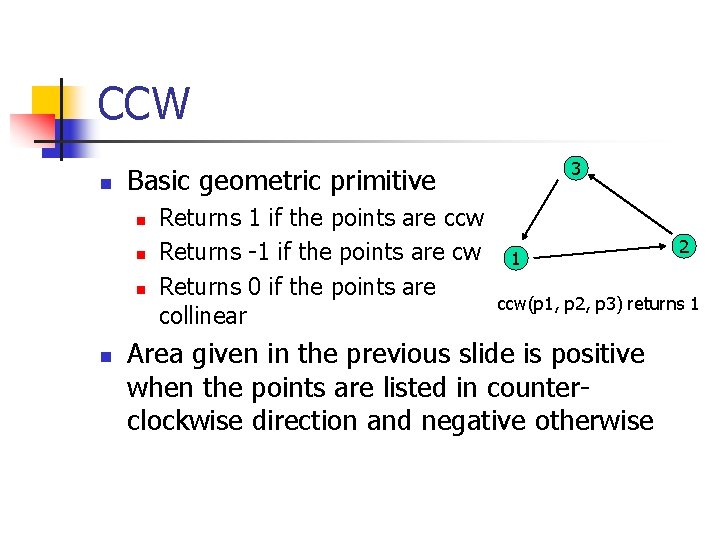
CCW n Basic geometric primitive n n 3 Returns 1 if the points are ccw Returns -1 if the points are cw Returns 0 if the points are collinear 1 2 ccw(p 1, p 2, p 3) returns 1 Area given in the previous slide is positive when the points are listed in counterclockwise direction and negative otherwise

Line segment intersection (I) n Given two line segments l 1 and l 2, determine if they intersect ? l 1. p 2 l 2. p 1 l 2. p 2 l 1. p 1 n is. Intersect = ccw(l 1. p 1, l 1. p 2, l 2. p 1) * ccw(l 1. p 1, l 1. p 2, l 2. p 2) <= 0 && ccw(l 2. p 1, l 2. p 2, l 1. p 1) * ccw(l 2. p 1, l 2. p 2, l 1. p 2) <= 0

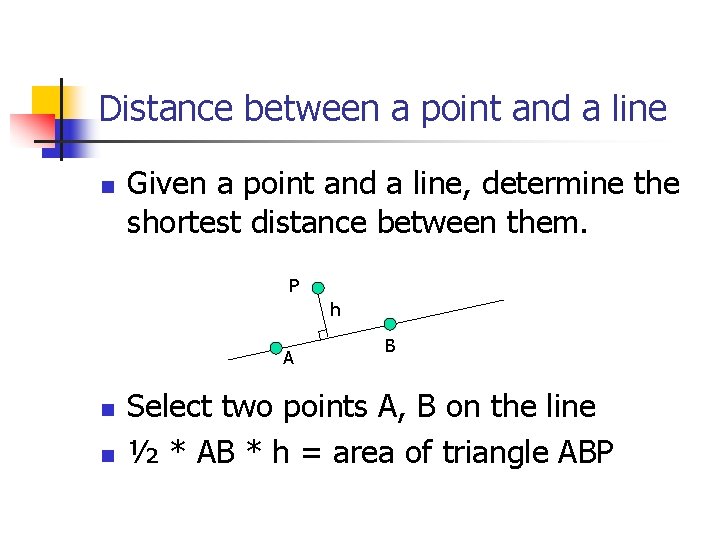
Distance between a point and a line n Given a point and a line, determine the shortest distance between them. P h A n n B Select two points A, B on the line ½ * AB * h = area of triangle ABP

Closest point (I) n n n Given a line L and a point P, find the point on L closest to P Recall that if u is a unit vector and v is any vector. The projection of v on u is given by (u. v)u u. v is the number k which minimized |v – ku|

Closest point (II) n n The theorem in the previous slide can only be applied to lines which pass through the origin This is sufficient to compute the general case as we can apply a translation if the line does not pass through the origin

Angle between two lines n n Represent lines as vectors u (a, b) and v (c, d) Definition of dot product: n n n u. v = |u||v|cos Θ = ac + bd u |u| = sqrt(u. u) Θ = cos-1(u. v / |u||v|) Θ v

Point in a polygon (I) n n n Given a point and a closed polygon, determine whether the point lies inside the polygon. Most algorithms extends a ray from the given point and considers the interaction of the polygon with the ray Such algorithms needs to handle the following boundary cases:

Point in a polygon (II) n n A standard way to resolve this issue is to adopt the following set of rules Edge crossing rules n n an upward edge includes its starting endpoint and excludes its endpoint a downward edge excludes its starting endpoint and includes its endpoint horizontal edges are excluded the edge-ray intersection point must be strictly right of the point P

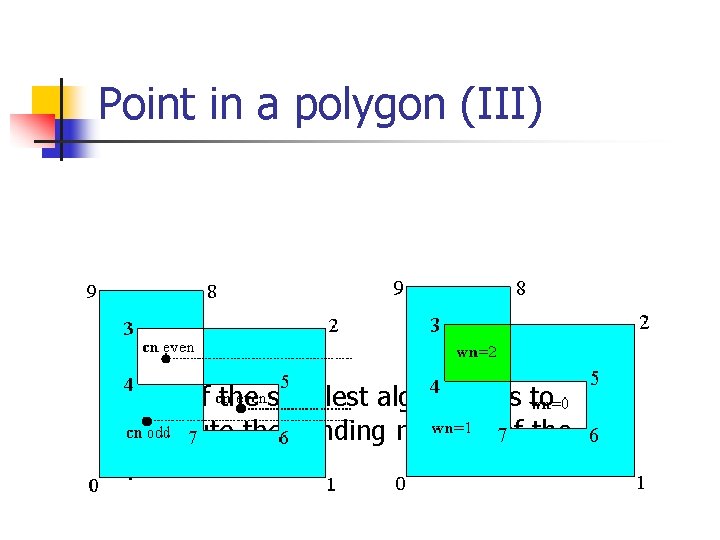
Point in a polygon (III) n One of the simplest algorithm is to compute the winding number of the point

Point in a polygon (IV) n Winding number n n number of times the polygon winds around the point Point is outside iff WN = 0 Upward edges => WN++ Downward edges => WN--

Point in a polygon (V) n // Input: P = a point, // V[] = vertex points of a polygon with V[n]=V[0] // Return: wn = the winding number (=0 only if P is outside V[]) int wn_Point. In. Poly(Point P, Point* V, int n) { int wn = 0; // the winding number counter // loop through all edges of the polygon for (int i=0; i<n; i++) { if (V[i]. y <= P. y) { if (V[i+1]. y > P. y) if (ccw( V[i], V[i+1], P) > 0) ++wn; } else { // V[i]. y > P. y if (V[i+1]. y <= P. y) if (ccw( V[i], V[i+1], P) < 0) --wn; } } return wn; } // edge from V[i] to V[i+1] // start y <= P. y // an upward crossing // P left of edge // have a valid up intersect // a downward crossing // P right of edge // have a valid down intersect

Convex hull (I) n n Given a set of points, determine the smallest convex set containing all the points A set S is convex if whenever two points P and Q are inside S, then the whole line segment PQ is also in S

Convex hull (II) n n One simple algorithm is Graham Scan, often cited as the first computational geometry algorithm Pseudocode n n n n Select the lowest leftmost point P[0] in S Sort the rest of the points in S according to the angle made with P[0], break ties base on distance to P[0] Let P[0. . n-1] be the sorted array of points Create an empty stack ST ST. push(P[n-1]) //P[n-1] must be on the hull ST. push(P[0]) //P[0] must be on the hull For i from 2 to n – 1 n n Let PT 1 denote the topmost point on ST Let PT 2 denote the second topmost point on ST while (ccw(PT 2, PT 1, P[i]) <= 0) ST. pop() ST. push(P[i])

Other issues n n n Case analysis Use of floating point numbers Overflow

References n n n http: //softsurfer. com/, Dan Sunday Algorithms, Robert Sedgewick Programming Challenges, Skiena and Revilla