COMPUTATIONAL FLUID DYNAMICS IN REALTIME An Introduction to

COMPUTATIONAL FLUID DYNAMICS IN REAL-TIME An Introduction to Simulation and Animation of Liquids and Gases

Considered Papers • Real-Time Fluid Dynamics for Games (2003) • by Jos Stam • previously worked on Maya; now with NVidia • covers gases • Realistic Animation of Liquids (1996) • by Nick Foster and Dimitri Metaxas • first attempt to solve Navier-Stokes in full 3 -D • Practical Animation of Liquids (2001) • by Nick Foster and Ronald Fedkiw • Particle-Based Fluid Simulation for Interactive Applications (2003) • by Matthias Mueller, David Charypar and Markus Gross

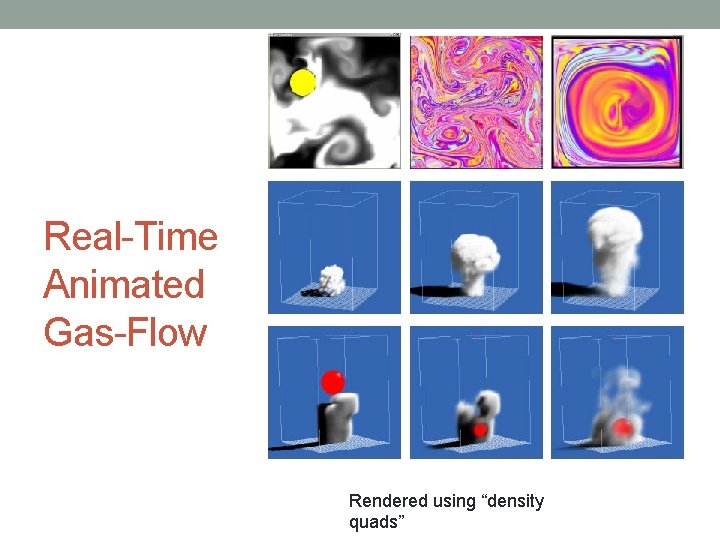
Real-Time Animated Gas-Flow Rendered using “density quads”

Grid-Based Water Animation Hybrid Surface Model

Particle-Based Water Animation Particles Point Splatting Iso-Surface (Marching Cubes)

Difference between liquids and gases • Gases have simpler free surfaces • Density provides enough information for renderer • For liquids we must also produce a smooth enough free surface at boundaries • Gases are compressible • Density of liquids, generally, never changes • Gases have often negligible viscosity • Liquids observe more obvious friction at boundary interfaces • But both are guided by the same equations

Physics of Fluids: The Navier-Stokes Equations • Velocity field: • Density distribution: u = velocity, ρ = density, κ = rate of diffusion, S = source influences • Conservation of mass: ∇⋅u=0 • i. e. , at any point in time, all velocities added together, cancel each other • Change of pressure: • Caused by movement of the liquid

Three components • Discretization • Grid • Particles • Algorithm to solve the mathematical model • Linear solver • More about this next time • Rendering • Billboarding • Particles • Point splatting • Iso-surfaces

Discretization • Old method: Propagate fluid state through a 2 -D or 3 -D grid • Every cell has density, velocity and pressure information • Liquid cells have 3 mutually exclusive states: • Full • Surface (boundary) • Empty • Object boundaries must coincide with the grid • New method: Use Smoothed-particle hydrodynamics • Particles that allow for smooth interpolation between their positions • Define rules for boundaries • At the system’s edges • For interfaces with other objects or fluids • Sources & Sinks

Grid-based algorithm for liquids (1996) 1. Define obstacles and initial configuration 2. Setup grid with initial configuration 3. Track surface in cells 4. Setup boundary conditions 5. Update velocity values 6. Update pressure values 7. Recalculate boundary information of surface cells 8. Update position of surface and objects 9. Go to step 3

Rendering (2001): Hybrid Surface Model • Move mass-less marker particles through the grid • Use algorithm (e. g. Marching Cubes) to determine a smooth iso-countour • Use other particle information and isocountour to make local changes

There is more to rendering • Transparency • Reflection • Refraction • Soft shadows

Fin • That’s it – For now!