Computational Finance Lecture 6 BlackScholes Formula Agenda n

Computational Finance Lecture 6 Black-Scholes Formula

Agenda n n How to use the B-S formula in Excel; Some possible extensions: n n n Stocks with dividends; Options on foreign currencies Implied volatility and historical volatility

Black-Scholes Formula n Stock price process: Drift: Volatility: Risk free interest rate:

Black-Scholes Formula n Option prices: n n Call option: Strike price Time to maturity Put option: Strike price Time to maturity

Black-Scholes Formula must satisfy the following PDE: n n and

Black-Scholes Formula n Black-Scholes formula: n European call: n European put: where

Example n What is the price of a European call option on a non-dividend-paying stock when the stock price is $52, the strike price is $50, the risk-free interest rate is 12% per annum and the volatility is 30% per annum and the time to maturity is three months?

Put-Call Parity Revisited n Suppose that a call and a put with the same strike price, the same time to maturity and on the same underlying stock. Then,

Some Extensions: Options on Dividend Stocks n Options on dividend stocks: n n Consider a 6 -month European call option on a stock when there are two dividend payments expected in two months and five months. The dividend of each payment is expected to be $0. 5. Current stock price $40, volatility 30% per annum, risk free interest: 9% per annum; Strike price $40

Some Extensions: Options on Dividend Stocks n Usually we can view the whole stock prices as the sum of two parts: n n n Riskless component that corresponds to the known dividend during the life of the option; Risky component. Reset to be the current stock price minus the present value of dividends. Then we can use the B-S formula.

Some Extensions: Currency Options n Options on foreign currencies: Consider a four-month European call option traded in the US market on the British pound. n n Current exchange rate US$1. 9/pound; Strike price: US$1. 95 Risk free interest rates: 8% in US, 11% in UK Exchange rate volatility: 20%

Some Extensions: Currency Options n The duplication argument will lead to

Some Extensions: Currency Options n Black-Scholes formula foreign currency options: n Call option: n Put option: where

Implied Volatility n Recall: n European call: n European put: where

Implied Volatility n n In the B-S formula, only one thing is unobservable: stock’s volatility. One way: Use the historical volatility to price options. But the historical information might be outdated.

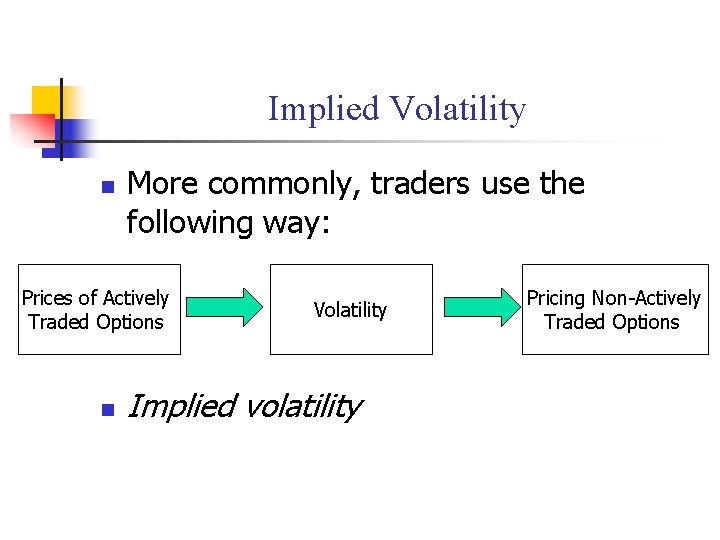
Implied Volatility n More commonly, traders use the following way: Prices of Actively Traded Options n Volatility Implied volatility Pricing Non-Actively Traded Options

Implied Volatility n Objective: n Note that where n Knowing or , solving for

Implied Volatility n n Example: Call option with strike price $30. Two stocks, A and B. A is more volatile and B is more placid. A: Price at maturity Payoffs n $10 $20 $30 $40 $50 $0 $10 $20 $0 $25 $0 $30 $0 $35 $5 $40 $10 B: Price at maturity Payoffs

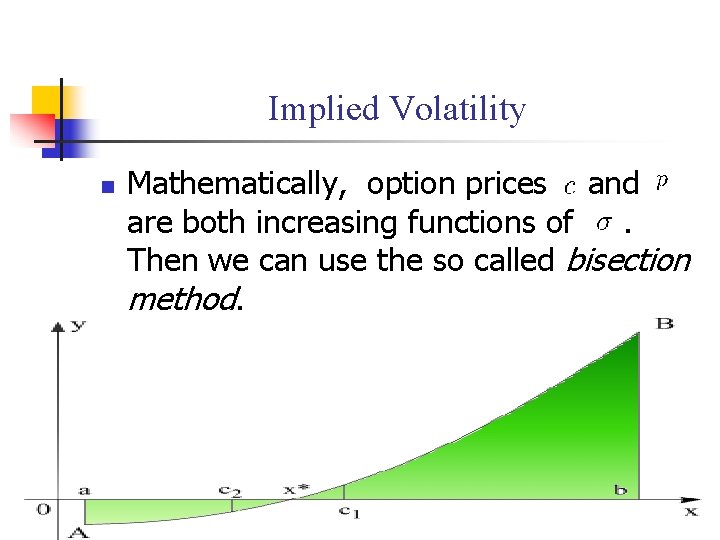
Implied Volatility n Mathematically, option prices and are both increasing functions of. Then we can use the so called bisection method.

Implied Volatility n Pseudo code: Do while ( Let If ); ; , then ; else ; End If End Loop

Implied Volatility n European call option: n n n Price: $1. 875 Underlying stock price: $21 Strike price: $20 Interest rate: 10% Time to maturity: 0. 25