Computational Complexity and Physics Scott Aaronson MIT New


















- Slides: 20

“Computational Complexity and Physics” Scott Aaronson (MIT) New Insights Into Computational Intractability Oxford University, October 3, 2013

Title is too broad! So, I’ll just give two “tales from the trenches”: - One about Boson. Sampling, one about black holes What you should take away: 1990 s: Today: Computational Complexity Shor & Grover Quantum Physics

Boson. Sampling (A. -Arkhipov 2011) A rudimentary type of quantum computing, involving only non-interacting photons Classical counterpart: Galton’s Board Replacing the balls by photons leads to famously counterintuitive phenomena, like the Hong-Ou-Mandel dip

In general, we consider a network of beamsplitters, with n input “modes” (locations) and m>>n output modes n identical photons enter, one per input mode Assume for simplicity they all leave in different modes—there are possibilities The beamsplitter network defines a column-orthonormal matrix A Cm n, such that where is the matrix permanent n n submatrix of A corresponding to S For simplicity, I’m ignoring outputs with ≥ 2 photons per mode

Example For Hong-Ou-Mandel experiment, In general, an n n complex permanent is a sum of n! terms, almost all of which cancel How hard is it to estimate the “tiny residue” left over? Answer: #P-complete, even for constant-factor approx (Contrast with nonnegative permanents!)

So, Can We Use Quantum Optics to Solve a #P-Complete Problem? That sounds way too good to be true… Explanation: If X is sub-unitary, then |Per(X)|2 will usually be exponentially small. So to get a reasonable estimate of |Per(X)|2 for a given X, we’d generally need to repeat the optical experiment exponentially many times

Better idea: Given A Cm n as input, let Boson. Sampling be the problem of merely sampling from the same distribution DA that the beamsplitter network samples from—the one defined by Pr[S]=|Per(AS)|2 Theorem (A. -Arkhipov 2011): Suppose Boson. Sampling is solvable in classical polynomial time. Then P#P=BPPNP Better Theorem: Suppose we can sample DA even approximately in classical polynomial time. Then in BPPNP, it’s possible to estimate Per(X), with high probability over a Gaussian random matrix Upshot: Compared to (say) Shor’s factoring algorithm, we get different/stronger evidence that a weaker system can do something classically hard

Experiments Last year, groups in Brisbane, Oxford, Rome, and Vienna reported the first 3 -photon Boson. Sampling experiments, confirming that the amplitudes were given by 3 x 3 permanents # of experiments > # of photons!

Obvious Challenges for Scaling Up: - Reliable single-photon sources (optical multiplexing? ) - Minimizing losses - Getting high probability of n-photon coincidence Goal (in our view): Scale to 10 -30 photons Don’t want to scale much beyond that—both because (1) you probably can’t without fault-tolerance, and (2) a classical computer probably couldn’t even verify the results! Theoretical Challenge: Argue that, even with photon losses and messier initial states, you’re still solving a classically-intractable sampling problem

Recent Criticisms of Gogolin et al. (ar. Xiv: 1306. 3995) Suppose you ignore which actual photodetectors light up, and count only the number of times each output configuration occurs. In that case, the Boson. Sampling distribution DA is exponentially-close to the uniform distribution U Response: Why would you ignore which detectors light up? ? The output of almost any algorithm is also gobbledygook if you ignore the order of the output bits…

Recent Criticisms of Gogolin et al. (ar. Xiv: 1306. 3995) OK, so maybe DA isn’t close to uniform. Still, the very same arguments we gave for why polynomial-time classical algorithms can’t sample DA, suggest that they can’t even distinguish DA from U! Response: That’s why we said to focus on 10 -30 photons—a range where a classical computer can verify a Boson. Sampling device’s output, but the Boson. Sampling device might be “faster”! (And 10 -30 photons is probably the best you can do anyway, without quantum fault-tolerance)

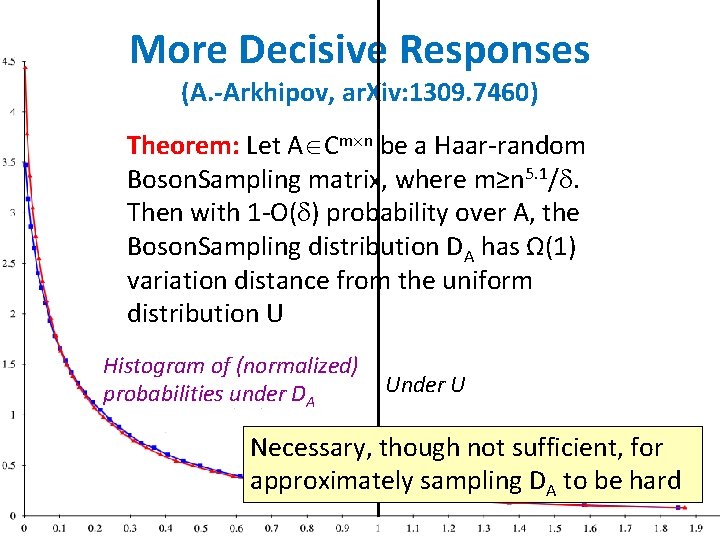
More Decisive Responses (A. -Arkhipov, ar. Xiv: 1309. 7460) Theorem: Let A Cm n be a Haar-random Boson. Sampling matrix, where m≥n 5. 1/. Then with 1 -O( ) probability over A, the Boson. Sampling distribution DA has Ω(1) variation distance from the uniform distribution U Histogram of (normalized) probabilities under DA Under U Necessary, though not sufficient, for approximately sampling DA to be hard

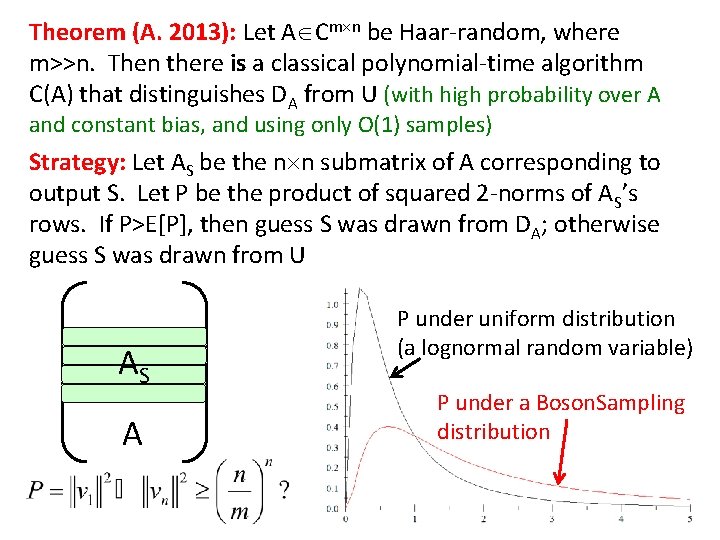
Theorem (A. 2013): Let A Cm n be Haar-random, where m>>n. Then there is a classical polynomial-time algorithm C(A) that distinguishes DA from U (with high probability over A and constant bias, and using only O(1) samples) Strategy: Let AS be the n n submatrix of A corresponding to output S. Let P be the product of squared 2 -norms of AS’s rows. If P>E[P], then guess S was drawn from DA; otherwise guess S was drawn from U AS A P under uniform distribution (a lognormal random variable) P under a Boson. Sampling distribution

Using Quantum Optics to Prove that the Permanent is #P-Complete [A. , Proc. Roy. Soc. 2011] Valiant showed that the permanent is #P-complete—but his proof required strange, custom-made gadgets We gave a new, arguably more transparent proof by combining three facts: (1) n-photon amplitudes correspond to n n permanents (2) Postselected quantum optics can simulate universal quantum computation [Knill-Laflamme-Milburn 2001] (3) Quantum computations can encode #P-complete quantities in their amplitudes

Black Holes and Computational Complexity? ? QAM AM QSZK BPP BQP YES!! Amazing connection made this year by Harlow & Hayden But first, we need to review 40 years of black hole history

Bekenstein 1972, Hawking 1975: Black holes have entropy and temperature! They emit radiation The Information Loss Problem: Calculations suggest that Hawking radiation is thermal—uncorrelated with whatever fell in. So, is infalling information lost forever? Would violate the unitarity / reversibility of QM OK then, assume the information somehow gets out! The Xeroxing Problem: How could the same qubit | fall inexorably toward the singularity, and emerge in Hawking radiation? Would violate the No-Cloning Theorem Black Hole Complementarity (Susskind, ‘t Hooft): An external observer can describe everything unitarily without including the interior at all! Interior should be seen as “just a scrambled re-encoding” of the exterior degrees of freedom

The Firewall Paradox (AMPS 2012) R = Faraway Hawking Radiation H = Just-Emitted Hawking Radiation Near-maximal entanglement B = Interior of “Old” Black Hole Also near-maximal entanglement Violates “monogamy of entanglement”! The same qubit can’t be maximally entangled with 2 things

Harlow-Hayden 2013 (ar. Xiv: 1301. 4504): Striking argument that Alice’s decoding task would require exponential time Complexity theory to the rescue of quantum field theory? ? The HH decoding problem: Given an n-qubit pure state | BHR produced by a known, poly-size quantum circuit. Promised that, by acting only on R (the “Hawking radiation”), it’s possible to distill an EPR pair (|00 +|11 )/√ 2 between R and B (the “black hole interior”). Distill such a pair, by applying a unitary transformation UR to the qubits in R. Theorem (HH): This decoding problem is QSZK-hard. So presumably intractable, unless QSZK=BQP (which we have oracle evidence against)!

Improvement (A. 2013): Suppose there are poly-size quantum circuits for the HH decoding problem. Then any OWF f: {0, 1}n {0, 1}p(n) can be inverted in quantum polynomial time. Proof: Assume for simplicity that f is injective. Consider Suppose applying UR to R decodes an EPR pair between R and B. Then for some {| x }x, we must have Generalizing to arbitrary OWFs requires Furthermore, to get perfect entanglement, we need | x =| x techniques similar to those used in HILL Theorem! for all x! So from U , we can get unitaries V, W such that R

Other Exciting Recent Complexity/Physics Connections Quantum PCP Conjecture. “Is approximate quantum MAX-k-SAT hard for quantum NP? ” If so, will require the construction exotic condensed matter systems, exhibiting room-temperature entanglement! Beautiful recent. Isurvey by Aharonov et al. many (ar. Xiv: 1309. 7495) hope for, and expect, more such striking connections! Using Entanglement to Steer Quantum Systems. Can Indeed, makingfor these connections possible use Bell inequality violation guaranteed randomness might be theblind most and important result of QC expansion (Vazirani-Vidick), authenticated quantum computing verifier, research—even if useful with a classical polynomial-time QMIP=MIP* QCs eventually get built! (Reichardt-Unger-Vazirani)…