Computational Biology Part 7 Similarity Functions and Sequence

Computational Biology, Part 7 Similarity Functions and Sequence Comparison with Dot Matrices Robert F. Murphy Copyright 1996, 1999 -2001. All rights reserved.

Similarity Functions � Used to facilitate comparison of two sequence elements � logical valued (true or false, 1 or 0) � test whether first argument matches (or could match) second argument � numerical valued � test degree to which first argument matches second

Logical valued similarity functions � Let Search(I)=‘A’ and Sequence(J)=‘R’ � A Function to Test for Exact Match � Match. Exact(Search(I), Sequence(J)) would return FALSE since A is not R � A Function to Test for Possibility of a Match using IUB codes for Incompletely Specified Bases � Match. Wild(Search(I), Sequence(J)) would return TRUE since R can be either A or G

Numerical valued similarity functions � return value could be probability (for DNA) � Let Search(I) = 'A' and Sequence(J) = 'R' � Similar. Nuc (Search(I), Sequence(J)) could return 0. 5 � since chances are 1 out of 2 that a purine is adenine � return value could be similarity (for protein) � Let Seq 1(I) = 'K' (lysine) and Seq 2(J) = 'R' (arginine) � Similar. Prot(Seq 1(I), Seq 2(J)) could return 0. 8 � since lysine is similar to arginine � usually use integer values for efficiency

Scoring (similarity) matrices � For each pair of characters in alphabet, value is proportional to degree of similarity (or other scoring criterion) between them � For proteins, most frequently used is Mutation Data Matrix from Dayhoff, 1978 (MDM 78)

Dayhoff PAM 250 similarity matrix (partial)

Origin of PAM 250 matrix � Take aligned set of closely related proteins � For each position in the set, find the most common amino acid observed there � Calculate the frequency with which each other amino acid is observed at that position � Combine frequencies from all positions to give table showing frequencies for each amino acid changing to each other amino acid � Take logarithm and normalize for frequency of each amino acid

Sequence comparison with dot matrices � Goal: Graphically display regions of similarity between two sequences (e. g. , domains in common between two proteins of suspected similar function)

Sequence comparison with dot matrices � Basic Method: For two sequences of lengths M and N, lay out an M by N grid (matrix) with one sequence across the top and one sequence down the left side. For each position in the grid, compare the sequence elements at the top (column) and to the left (row). If and only if they are the same, place a dot at that position.

Sequence comparison with dot matrices - References � W. M. Fitch. An improved method of testing for evolutionary homology. J. Mol. Biol. 16: 9 -16 (1966) � W. M. Fitch. Locating gaps in amino acid sequences to optimize the homology between two proteins. Biochem. Genet. 3: 99 -108 (1969)

Sequence comparison with dot matrices - References � A. J. Gibbs & G. A. Mc. Intyre. The diagram, a method for comparing sequences. Its use with amino acid and nucleotide sequences. Eur. J. Biochem. 16: 1 -11 (1970) � A. D. Mc. Lachlan. Test for comparing related amino acid sequences: cytochrome c and cytochrome c 551. J. Mol. Biol. 61: 409 -424 (1971)

Sequence comparison with dot matrices - References � J. Pustell & F. C. Kafatos. A high speed, high capacity homology matrix: zooming through SV 40 and polyoma. Nucleic Acids Res. 10: 4765 -4782 (1982) � J. Pustell & F. C. Kafatos. A convenient and adaptable package of computer programs for DNA and protein sequence management, analysis and homology determination. Nucleic Acids Res. 12: 643 -655 (1984)

Examples for protein sequences � (Demonstration A 5, Sequence 1 vs. 2) � (Demonstration A 5, Sequence 2 vs. 3)

Interpretation of dot matrices � Regions of similarity appear as diagonal runs of dots � Reverse diagonals (perpendicular to diagonal) indicate inversions � Reverse diagonals crossing diagonals (Xs) indicate palindromes � (Demonstration A 5, Sequence 4 vs. 4)

Interpretation of dot matrices � Can link or "join" separate diagonals to form alignment with "gaps" � Each a. a. or base can only be used once � Can't trace vertically or horizontally � Can't double back � A gap is introduced by each vertical or horizontal skip

Uses for dot matrices � Can use dot matrices to align two proteins or two nucleic acid sequences � Can use to find amino acid repeats within a protein by comparing a protein sequence to itself � Repeats appear as a set of diagonal runs stacked vertically and/or horizontally � (Demonstration A 5, Sequence 5 vs. 6)

Uses for dot matrices � Can use to find self base-pairing of an RNA (e. g. , t. RNA) by comparing a sequence to itself complemented and reversed � Excellent approach for finding sequence transpositions

Filtering to remove “noise” � A problem with dot matrices for long sequences is that they can be very noisy due to lots of insignificant matches (i. e. , one A) � Solution use a window and a threshold � compare character by character within a window (have to choose window size) � require certain fraction of matches within window in order to display it with a “dot”

Example spreadsheet with window � (Demonstration A 6)

How do we choose a window size? � Window size changes with goal of analysis � size of average exon � size of average protein structural element � size of gene promoter � size of enzyme active site

How do we choose a threshold value? � Threshold based on statistics � using shuffled actual sequence average (m) and s. d. ( ) of match scores of shuffled sequence � convert original (unshuffled) scores (x) to Z scores � find • Z = (x - m)/ � use threshold Z of of 3 to 6 � using analysis of other sets of sequences � provides “objective” standard of significance

Displaying matrices by Pustell method with Mac. Vector � Goal: Determine differences in arrangements of elements of p. Bluescript family of vectors � Starting point: Use sequences of three of the members of the family: open the first three files in the Common Vectors: Bluescript folder.
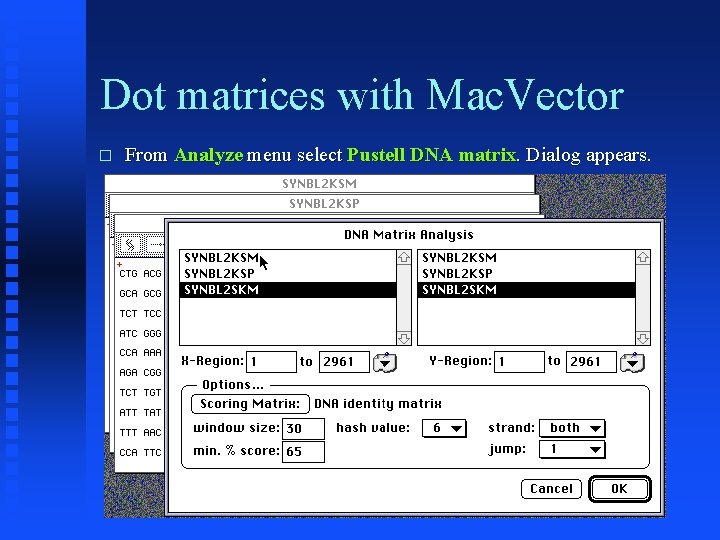
Dot matrices with Mac. Vector � From Analyze menu select Pustell DNA matrix. Dialog appears.
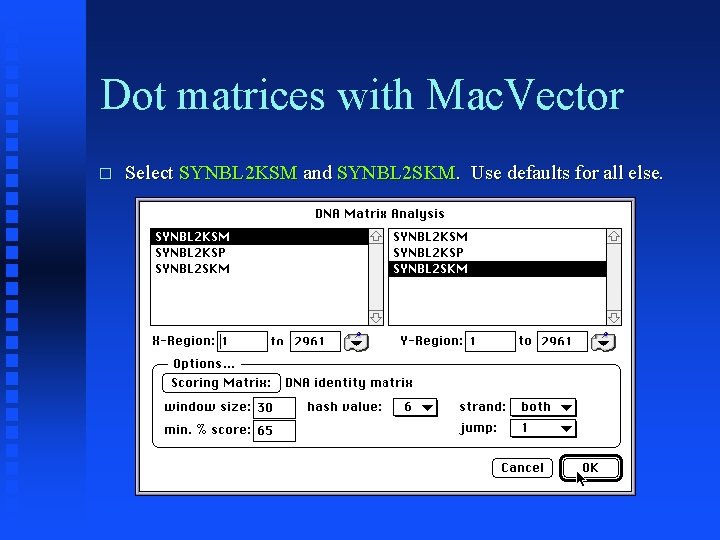
Dot matrices with Mac. Vector � Select SYNBL 2 KSM and SYNBL 2 SKM. Use defaults for all else.

Dot matrices with Mac. Vector � 23 reagons of homology (“diagonals”) obtained. Request “Matrix map” only (don’t need “Aligned sequences”)

Dot matrices with Mac. Vector � Note inversion near nucleotide 700 (the direction of the polylinker is reversed between the two vectors)
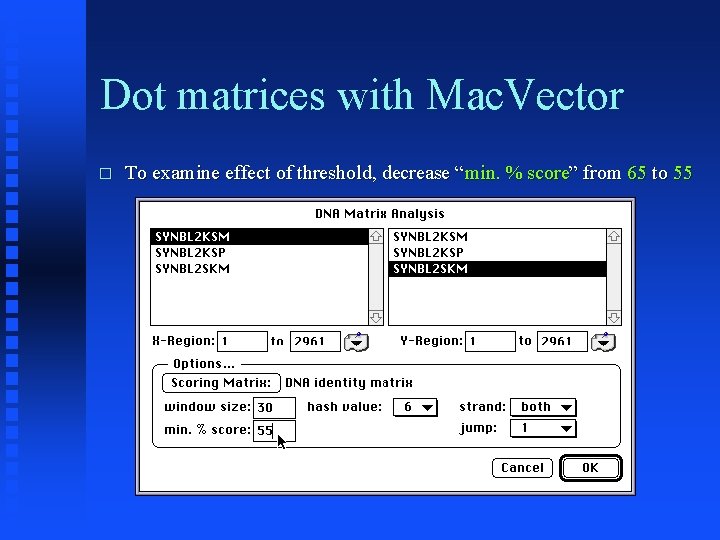
Dot matrices with Mac. Vector � To examine effect of threshold, decrease “min. % score” from 65 to 55
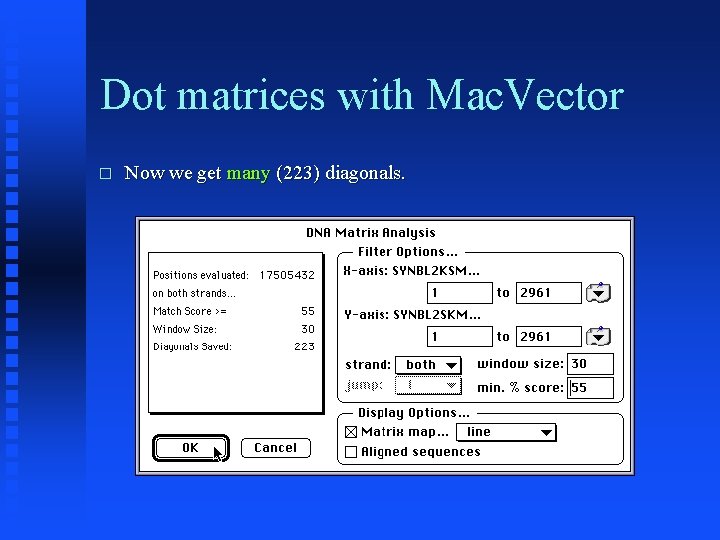
Dot matrices with Mac. Vector � Now we get many (223) diagonals.

Dot matrices with Mac. Vector � Note presence of many short regions of at least 55% homology.
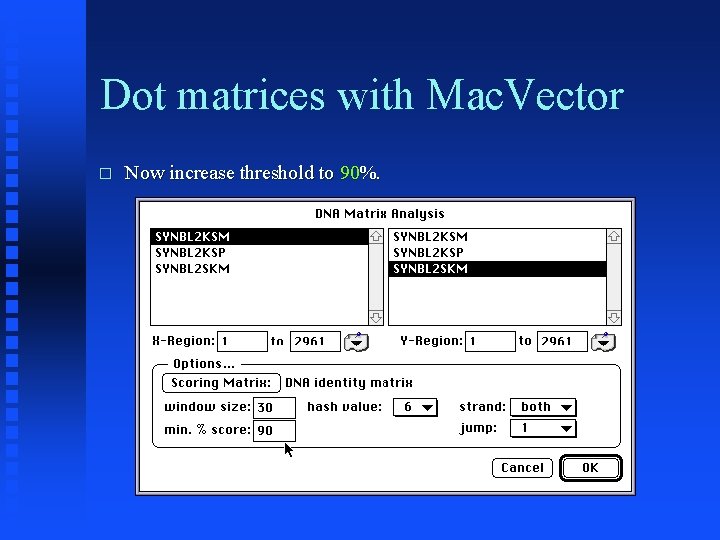
Dot matrices with Mac. Vector � Now increase threshold to 90%.
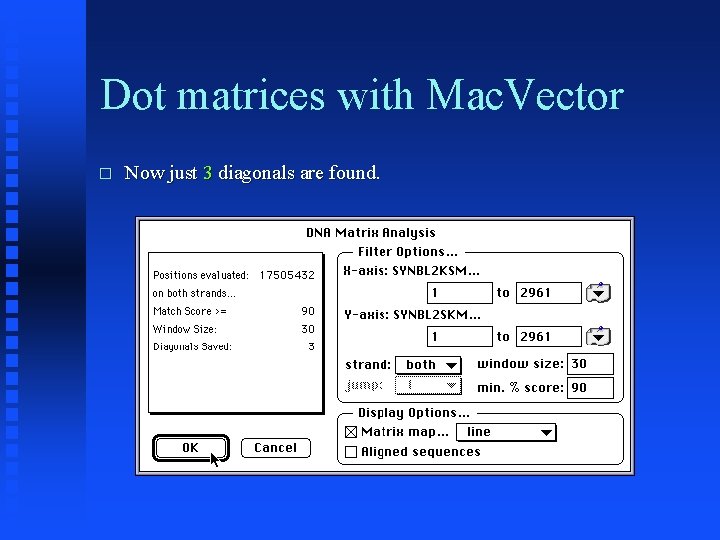
Dot matrices with Mac. Vector � Now just 3 diagonals are found.

Dot matrices with Mac. Vector � Note absence of short homologous regions (“noise”).
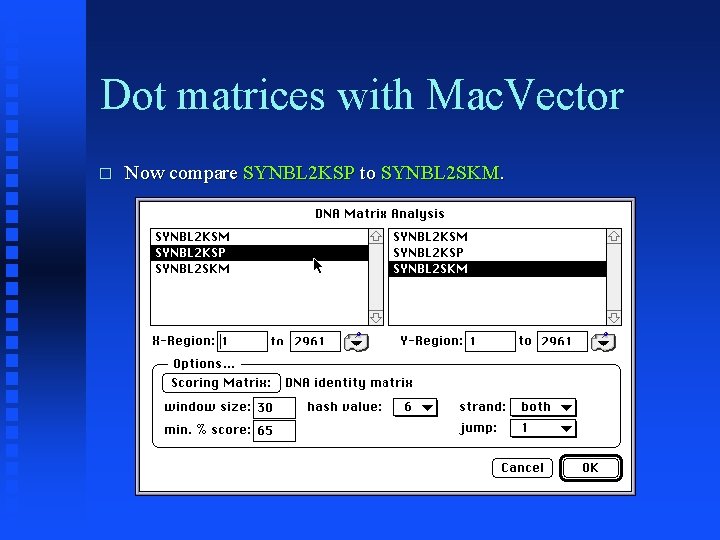
Dot matrices with Mac. Vector � Now compare SYNBL 2 KSP to SYNBL 2 SKM.

Dot matrices with Mac. Vector � 22 diagonals found using default settings.

Dot matrices with Mac. Vector � Note second large inversion at one end of sequences.

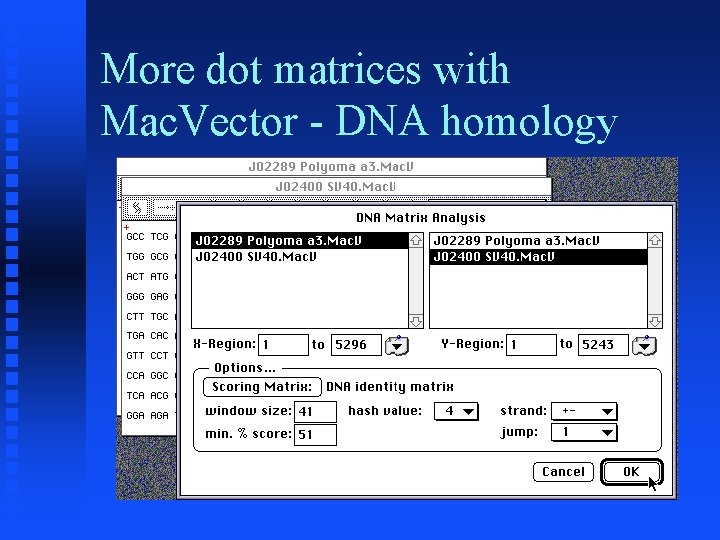
More dot matrices with Mac. Vector - DNA homology � Goal: Duplicate Figure 6 of Chapter 3 of Sequence Analysis Primer � Get Accession numbers J 02289 (Polyoma) and J 02400 (SV 40) from Entrez � Do Pustell DNA Matrix analysis using parameters similar to those used in text (window size = 41, %identity = 51)
More dot matrices with Mac. Vector - DNA homology
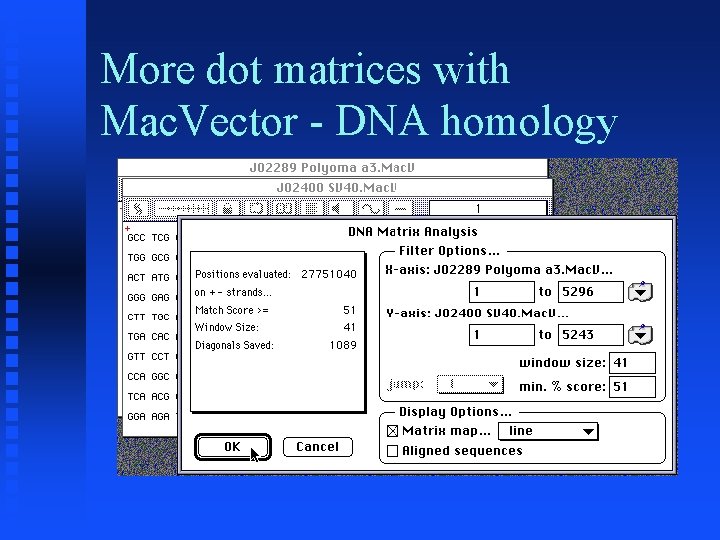
More dot matrices with Mac. Vector - DNA homology

More dot matrices with Mac. Vector - DNA homology

More dot matrices with Mac. Vector - protein homology � Goal: Reproduce Figure 15 from Chapter 3 of Sequence Analysis Primer � Get Accession numbers P 17678 (Chicken) and X 17254 (human) erythroid transcription factors using Entrez � Do Pustell Protein Matrix Analysis

Reading for next class � B & O, Chapter 7 just pp. 145 -155 � Additional optional reading: Sequence Analysis Primer, pp. 124 -134 “Dynamic Programming Methods” (on web site as Reading 1) � (03 -510) Durbin et al, Sections 2. 1 - 2. 4 � Everybody: Look over paper by Needleman and Wunsch on web site (Reading 2)

Summary, Part 7 � Similarity functions or similarity matrices describe (quantitatively) the degree of similarity between two sequence elements (bases or amino acids) � The Dayhoff MDM 78 matrix is a similarity matrix commonly used to estimate the degree to which a change from one amino acid to another can be “tolerated” in a protein

Summary, Part 7 � Dot matrices graphically present regions of identity or similarity between two sequences � The use of windows and thresholds can reduce “noise” in dot matrices � Inversions, duplications and palindromes have unique “signatures” in dot matrices
- Slides: 43