Computational Biology Information encoded in biological systems Onedimensional

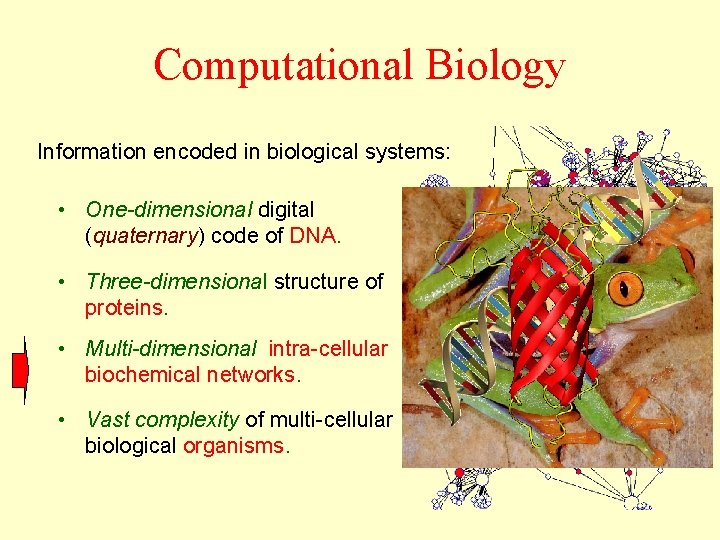
Computational Biology Information encoded in biological systems: • One-dimensional digital (quaternary) code of DNA. • Three-dimensional structure of proteins. • Multi-dimensional intra-cellular biochemical networks. • Vast complexity of multi-cellular biological organisms.

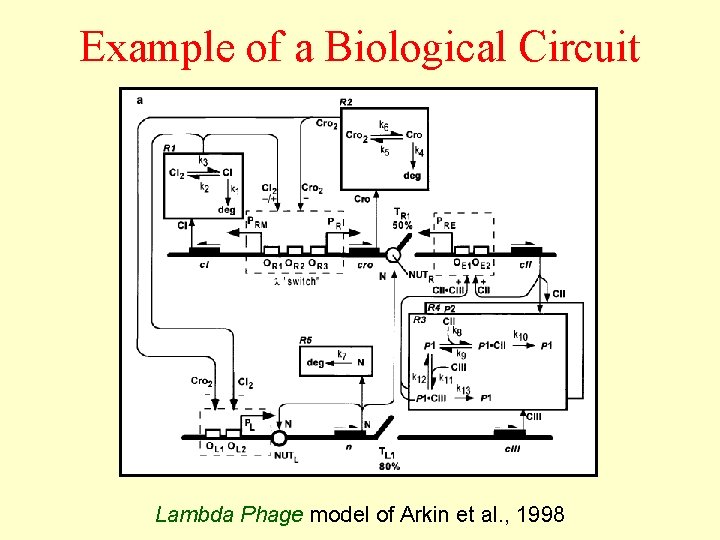
Example of a Biological Circuit Lambda Phage model of Arkin et al. , 1998

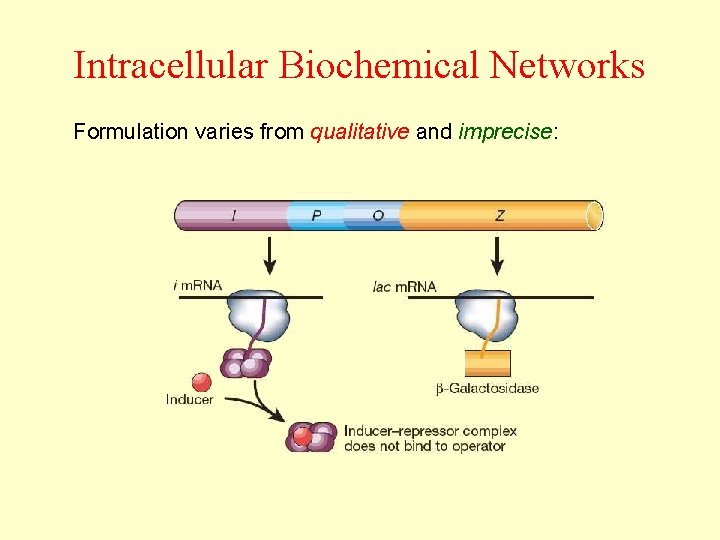
Intracellular Biochemical Networks Formulation varies from qualitative and imprecise:

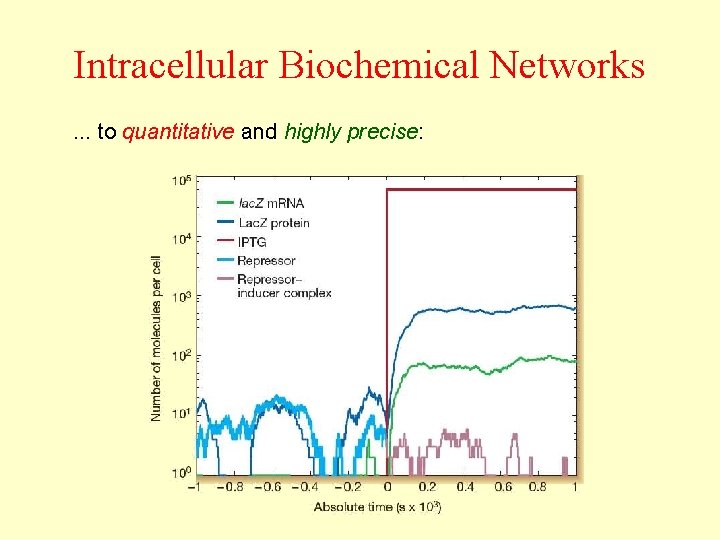
Intracellular Biochemical Networks. . . to quantitative and highly precise:

Biochemical Reactions Lingua Franca of computational biology. Reaction 1 molecule of type A combines with 2 molecules of type B to produce 2 molecules of type C. Reaction is annotated with a rate constant and physical constraints (localization, gradients, etc. )

Biochemical Reactions Lingua Franca of computational biology. Reaction Species: • Elementary molecules (e. g. , hydrogen, phosphorous, . . . ) • Complex molecules (e. g. , proteins, enzymes, RNA. . . ) Reaction: • Elementary step (e. g. , ) • Conglomeration of steps (e. g. , transcription of gene product)

Biochemical Reactions Lingua Franca of computational biology. Coupled Set Reactions R 1 R 2 R 3 Goal: given initial conditions, analyze (predict) the evolution of such a system.

Biochemical Reactions Convential Approach: numerical calculations based on coupled ordinary differential equations. • Computationally challenging (sometimes intractable). • Assumes that molecular quantities are continuous values that vary deterministically over time.

Biochemical Reactions Convential Approach: numerical calculations based on coupled ordinary differential equations. • In intracellular networks, the number of molecules of each complex type is generally small (10 s, 100 s, at most 1000 s). • Individual reactions matter.

Gillespie’s Framework Track precise (integer) quantities of molecular species. “States” A Reactions B C S 1 4 7 5 R 1 S 2 2 6 8 R 2 S 3 22 0 997 R 3 A reaction transforms one state into another: e. g. ,

Stochastic Simulation S 1 = [5, 5, 5] 0 R 1 R 2 R 3 Ri Choose the next reaction according to: where

Stochastic Simulation S 1 = [5, 5, 5] 0 R 1 R 2 R 3 Ri Choose the time of the next reaction according to:

S 1 = [5, 5, 5] 0 R 1 R 2 Stochastic Simulation R 3 See D. Gillespie, “Exact Stochastic Simulation of Coupled Chemical Reactions”, J. Phys. Chem. 1977

S 1 = [5, 5, 5] 0 Stochastic Simulation Choose R 3 and t = 3 seconds. R 1 R 2 R 3 S 2 = [4, 7, 4] 3 Choose R 1 and t = 1 seconds. S 3 = [2, 6, 7] 4 Choose R 3 and t = 2 seconds. S 4 = [1, 8, 6] 6 Choose R 2 and t = 1 seconds.

S 1 = [5, 5, 5] 0 Stochastic Simulation Choose R 3 and t = 3 seconds. S 2 = [4, 7, 4] 37 Choose R 1 and t = 1 seconds. S 3 = [2, 6, 7] 4 Choose R 3 and t = 2 seconds. S 4 = [1, 8, 6] 6 Choose R 2 and t = 1 seconds.