Computation of Force Closure Grasps from Finite Contact

Computation of Force Closure Grasps from Finite Contact Point Set Nattee Niparnan Advisor: Dr. Attawith Sudsang

General Outline l l l The story so far: robotic grasping What lies behind us: literature review Where shall we go: the problem Who walk along the same road: related work Problem Detail l Grasping Basic How do we reach the goal: attack point Boring stuffs l work plan, objective, scopes, benefit

Robotic Grasping l To hold an object firmly l Prevent motion of an object

State of the Art

Ultimate Goal of Grasping Sense the object l Calculate grasping position l Initiate a grasp l

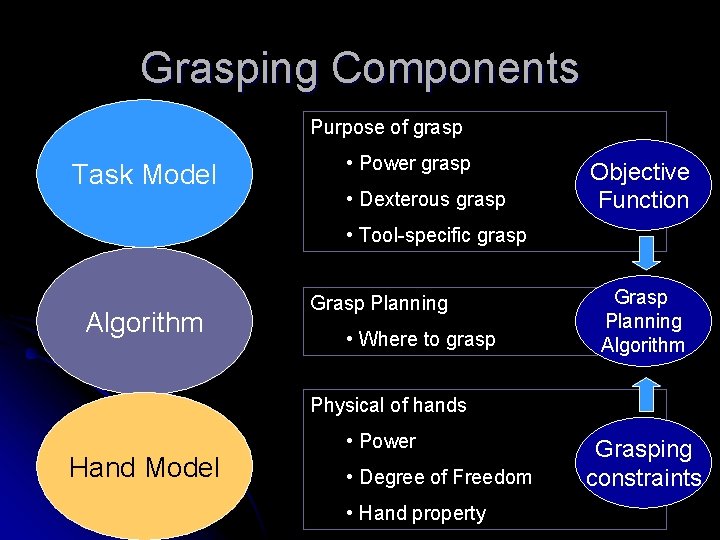
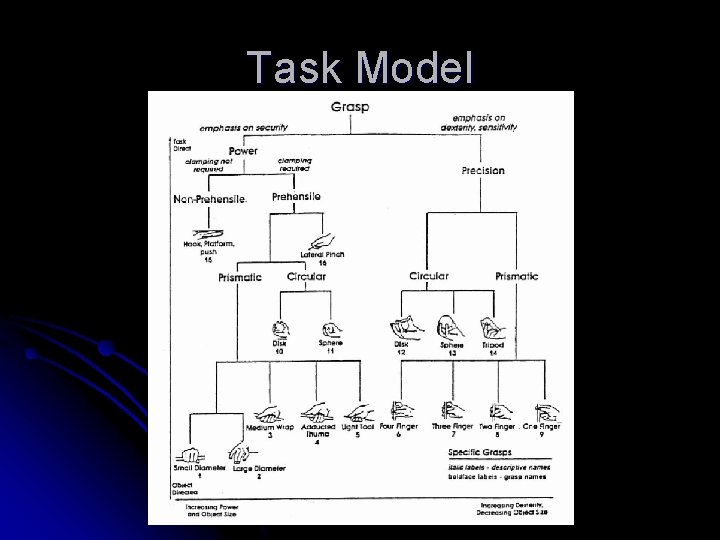
Grasping Components Purpose of grasp Task Model • Power grasp • Dexterous grasp Objective Function • Tool-specific grasp Algorithm Grasp Planning • Where to grasp Grasp Planning Algorithm Physical of hands Hand Model • Power • Degree of Freedom • Hand property Grasping constraints

Example: Grasping a Hammer l Task: Moving a Hammer l Maximize l stability Task: Using a Hammer l Maximize head speed Hand: Parallel Jaw Gripper l Hand: 4 -fingered Hand l

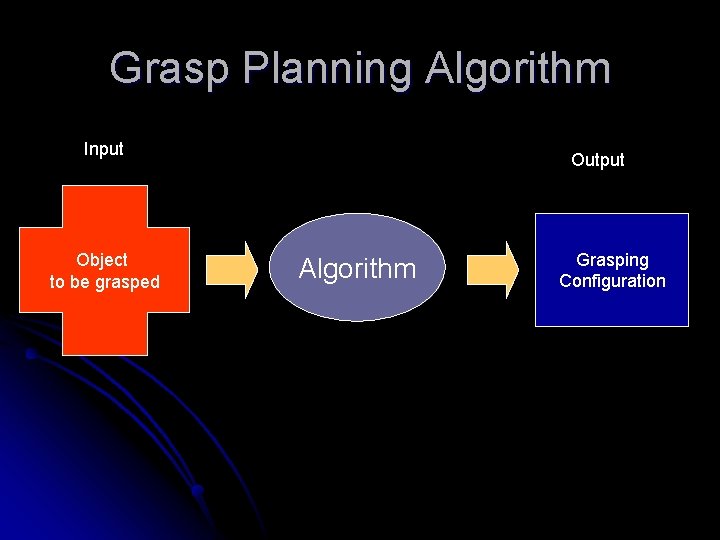
Grasp Planning Algorithm Input Object to be grasped Output Algorithm Grasping Configuration

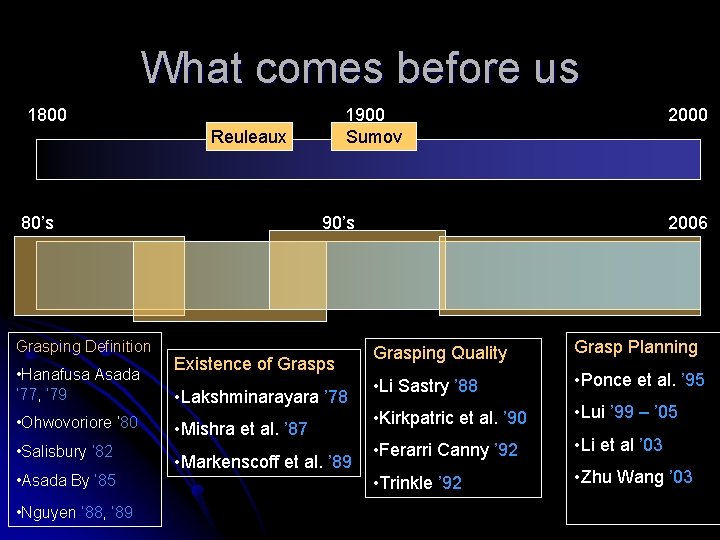
What comes before us 1800 1900 Sumov Reuleaux 80’s Grasping Definition • Hanafusa Asada ’ 77, ’ 79 • Ohwovoriore ‘ 80 • Salisbury ’ 82 • Asada By ’ 85 • Nguyen ’ 88, ’ 89 2000 90’s Existence of Grasps • Lakshminarayara ’ 78 • Mishra et al. ’ 87 • Markenscoff et al. ’ 89 2006 Grasping Quality Grasp Planning • Li Sastry ’ 88 • Ponce et al. ’ 95 • Kirkpatric et al. ’ 90 • Lui ’ 99 – ’ 05 • Ferarri Canny ’ 92 • Li et al ’ 03 • Trinkle ’ 92 • Zhu Wang ’ 03

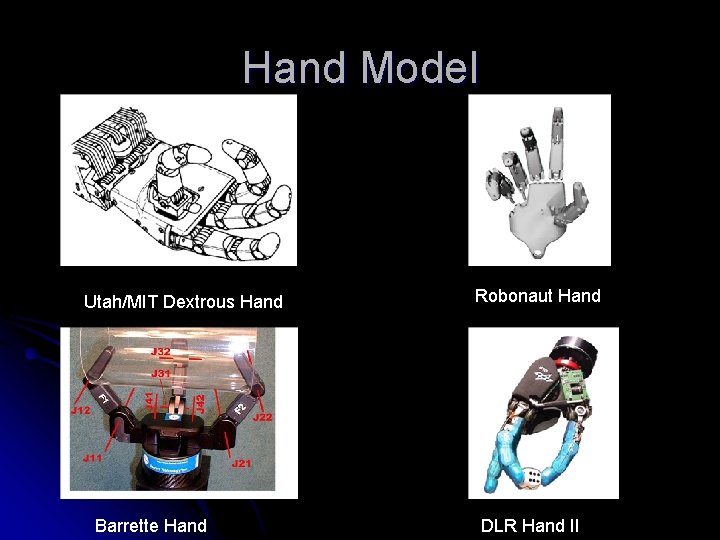
Hand Model Utah/MIT Dextrous Hand Barrette Hand Robonaut Hand DLR Hand II

Task Model

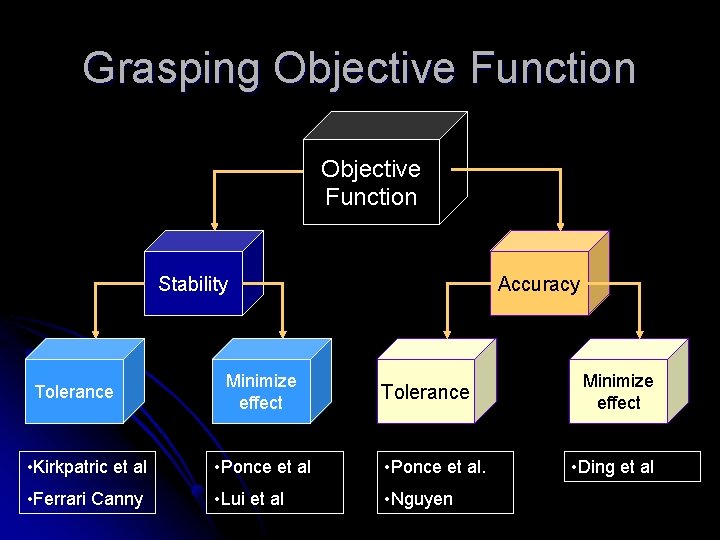
Grasping Objective Function Stability Tolerance Minimize effect Accuracy Tolerance • Kirkpatric et al • Ponce et al. • Ferrari Canny • Lui et al • Nguyen Minimize effect • Ding et al

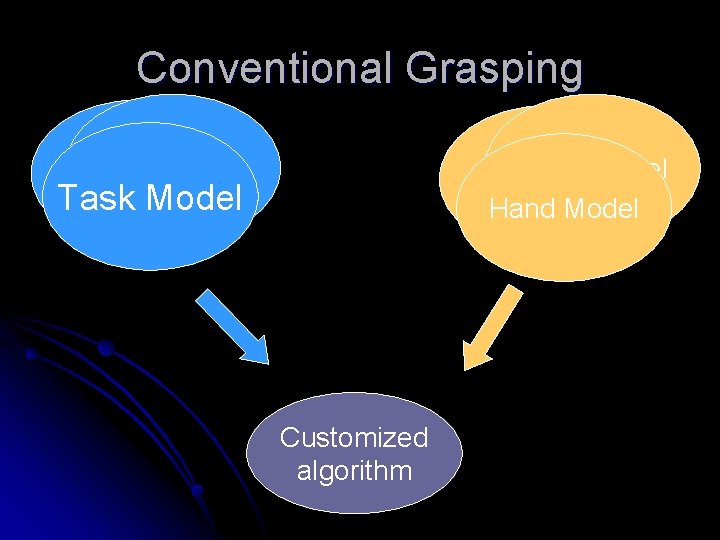
Conventional Grasping Objective Function Task Model Hand Model Customized algorithm

Issues l No generally good grasp!!! l No general task model l No general hand model l Different measurement and constraints l Object modeling l Modeling accuracy

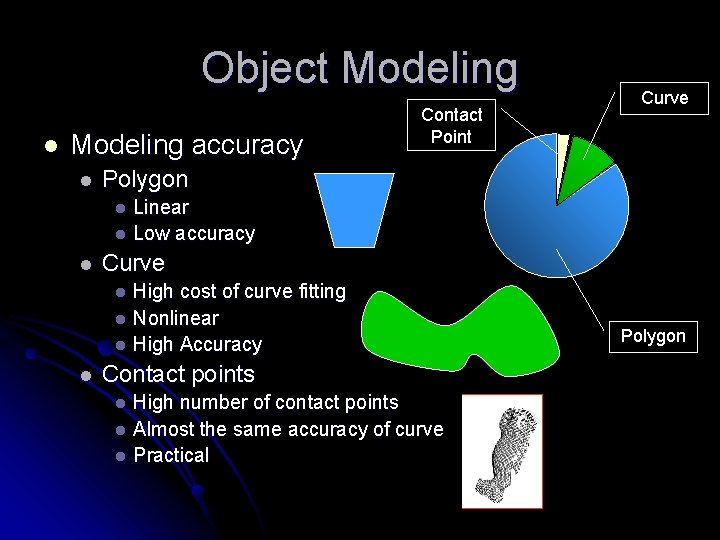
Object Modeling l Modeling accuracy l Contact Point Curve Polygon Linear l Low accuracy l l Curve High cost of curve fitting l Nonlinear l High Accuracy l l Contact points High number of contact points l Almost the same accuracy of curve l Practical l Polygon

Where shall we go l New grasp planning framework Task Model Use Contact Points (Model-less) Hand Model Generalized Algorithm Take no a priori knowledge

Where shall we go l Instead of finding one best grasp l Just l find “firm” grasps Find lots of grasps l Use no a priori knowledge of Task/Hand l Let task model and hand model choose appropriate grasp l Using contact points l Model-less la input large number of input

Is It Hard? l Consider one single “firm grasp” problem in Polygonal model l Multiple grasping solution? l l Computational intensive Linear Programming / Ray Shooting / Point Inclusion Almost unobtainable until recently With contact point model? l l l Polygon around 10 -20 faces Contact Point around 1000 contact points Much more computational extensive

Challenge l SPEED!!!

Usage of the Result l Given Task/Hand l enumerate solution to find the best one l O(n) l Result is associated to the object l Normal use usually involve multiple step l Regrasp

Problem Statement: First Draft Given a set of contact points l Find l l As many good grasps as possible l In a short time

Naïve Approach l one single “firm grasp” problem l Still is an active topic l l l Lui ’ 99 – ’ 05 Li et al ’ 03 Zhu Wang ’ 03 Borst et al ’ 03 Zhu et al ’ 04

Naïve Approach l Finding all solutions l Combinatorial Problem l l 1000 points 4 fingers Must check 1000 4 O(N 4) Search space

Who walk along the same road l Contact point input l l l Wallack Canny ‘ 94 Brost Goldberg ‘ 96 Wang ‘ 00 l l Multiple solutions l van der Stappen ‘ 04 Multiple solutions & Contact point Input l None. . .

Problem Detail

Grasping Basic l Force Closure l Formal definition of firm grasp l “Hand can influence the object such that any external disturbance can be nullified”

Influence of a hand via contact points between a hand an object l Described by l l Contact positions ( r ) l Contact directions ( n )

Influence of a Contact Point l Force (contact direction) l Force l vector ( f ) Torque (contact position & direction) l Torque vector ( r x f )

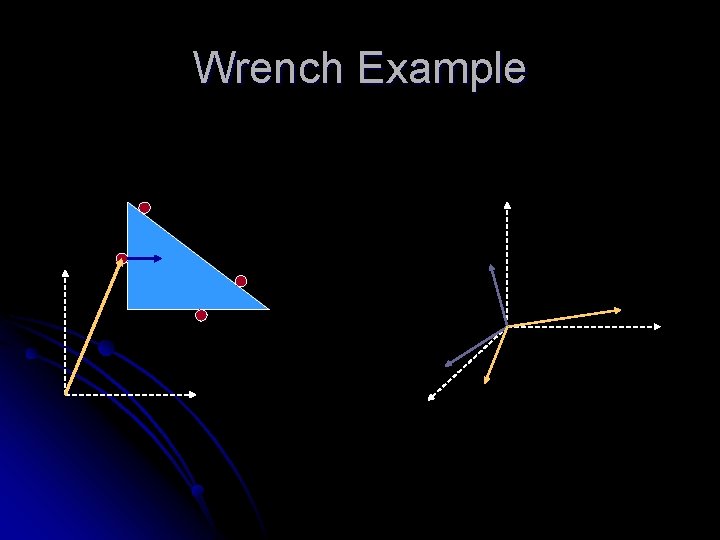
Wrench l To combine force and torque into one component l l Easier to describe Wrench = force vector concatenates with torque vector w = ( f, r x f ) Model a contact point by a wrench Space Dimension Force Dimension Torque Dimension Wrench Dimension 2 D 3 D 1 D 3 D 3 D 6 D

Wrench Example

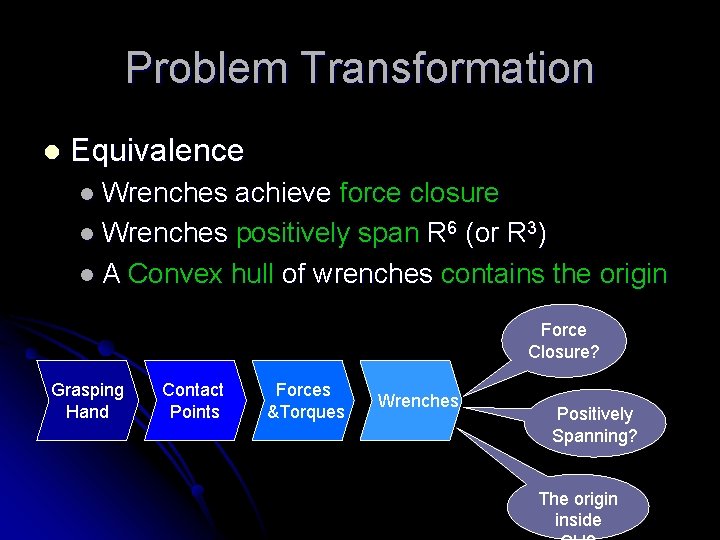
Force Closure in terms of Wrenches External disturbance can also be written as a wrench l Contact points can exert l l Their respective wrenches l Also l positive combinations of the wrenches Force Closure = any wrench can be expressed by a positive combination of contact point wrenches Grasping Hand Contact Points Forces &Torques Wrenches

Problem Transformation l Equivalence l Wrenches achieve force closure l Wrenches positively span R 6 (or R 3) l A Convex hull of wrenches contains the origin Force Closure? Grasping Hand Contact Points Forces &Torques Wrenches Positively Spanning? The origin inside

Positively Spanning l any vector can be expressed by a positive combination of given vectors

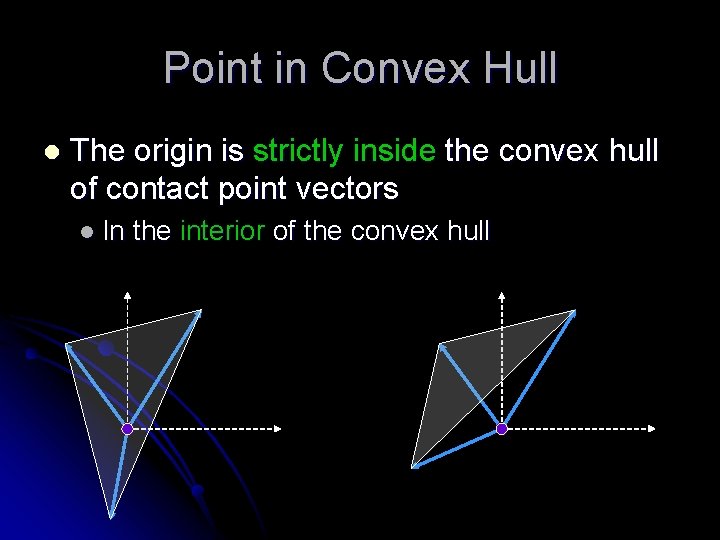
Point in Convex Hull l The origin is strictly inside the convex hull of contact point vectors l In the interior of the convex hull

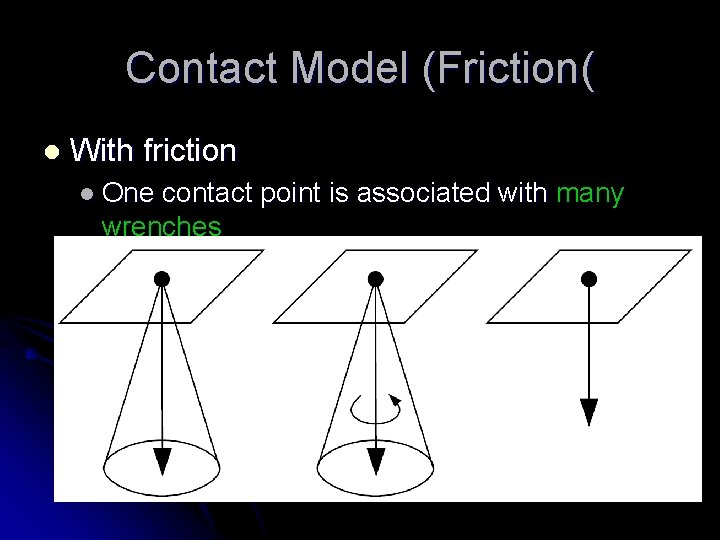
Contact Model (Friction( l With friction l One contact point is associated with many wrenches

Check Point l Grasping problem is l. A mathematical problem l A computational geometry problem l Emphasize on deriving of an efficient algorithm for reporting several solutions from contact point input

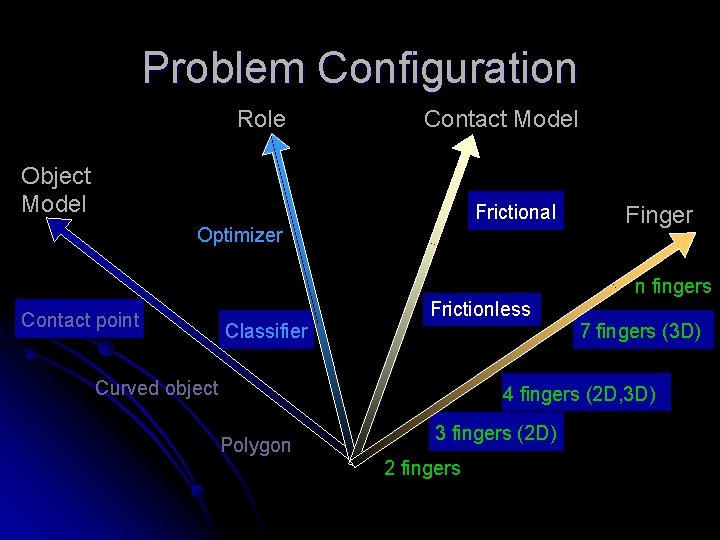
Problem Configuration Role Contact Model Object Model Frictional Optimizer Finger n fingers Contact point Frictionless Classifier 7 fingers (3 D) Curved object 4 fingers (2 D, 3 D) Polygon 3 fingers (2 D) 2 fingers

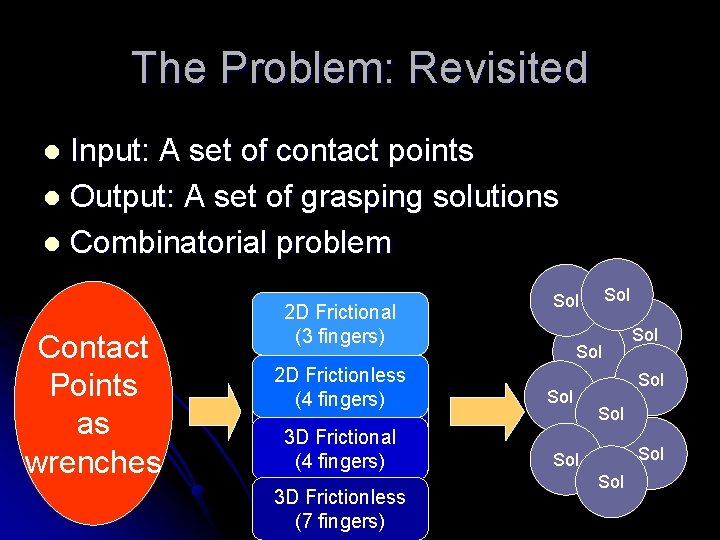
The Problem: Revisited Input: A set of contact points l Output: A set of grasping solutions l Combinatorial problem l Contact Points as wrenches 2 D Frictional (3 fingers) 2 D Frictionless (4 fingers) Algorithm 3 D Frictional (4 fingers) 3 D Frictionless (7 fingers) Sol Sol Sol

How do we reach the goal l Exploit multiple solution nature of the problem l Try to use pre-computation l Sorting, l searching, suitable data structure, etc. Problem reformulation l Reduce dimension of wrench space

Work Plan l l l l l Study the works in the related fields Preliminary works on a heuristic algorithm Study a reformulation of the problem In-depth study of grasp planning algorithms Perform extensive comparison of various grasping condition Develop algorithms Comparison Publish a journal article Prepare and engage in a thesis defense

Recent Works l l l Fast Computation of 4 -Fingered Force-Closure Grasps from Surface Points. Proc. of the IEEE/RSJ International Conf. on Intelligent Robots and Systems, pp 3692 -3697, 2004. Regrasp Planning of Four-Fingered Hand for Parallel Grasp of a Polygonal Object. Proc. of the IEEE International Conf. on Robotics and Automation, pp 791 -796, 2005. A Heuristic Approach for Computing Frictionless Force-Closure Grasps of 2 D Objects from Contact Point Set. Proc. of the IEEE International Conference on Robotics, Automation and Mechatronics, 2006 Planning Optimal Force-Closure Grasps for Curved Objects by Genetic Algorithm. Proc. of the IEEE International Conference on Robotics, Automation and Mechatronics, 2006 4 -Fingered Force-Closure Grasps from Surface Points using Genetic Algorithm. Proc. of the IEEE International Conference on Robotics, Automation and Mechatronics, 2006

Objective l To develop efficient algorithms that report several force closure grasps from a set of finite contact points

Scope of the Research Considers force closure grasping in both 2 D and 3 D in friction and frictionless case l Derived algorithms must work faster than an enumerative approach that uses the fastest computation l Performance measurement can be either an actual running time (in case of a heuristic algorithm) or a complexity analysis (in case of a complete algorithm) l

Scope of the Research 2 D Frictional (3 fingers) 2 D Frictionless (4 fingers) 3 D Frictional (4 fingers) 3 D Frictionless (7 fingers) Compare with the best known “single solution” algorithm Evidence of superiority • Proof of complexity analysis Evidence of superiority • Proof. Evidence of Time complexity analysis of superiority • Running Comparison • Proof of Time complexity analysis • Running Comparison • Running Time Comparison

Expected Contribution l Having algorithms that report several force closure grasps from a set of discrete contact points.

Thank You Comments are heartily welcomed

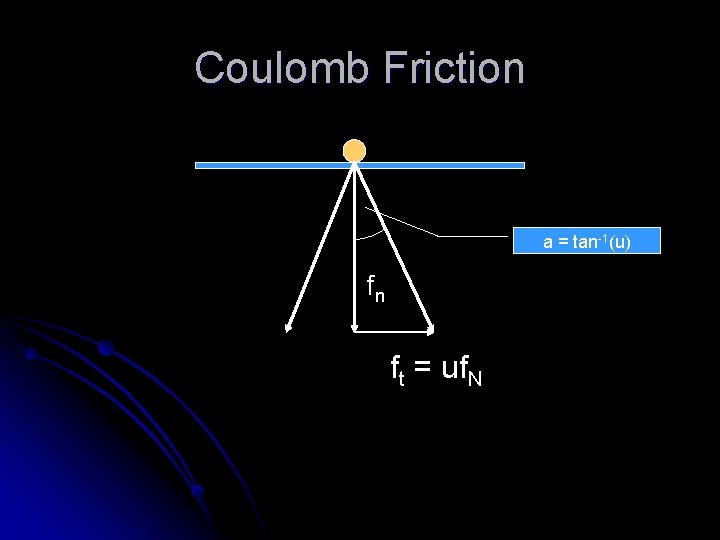
Coulomb Friction a = tan-1(u) fn ft = uf. N

DLR Hand l Sensor per each finger l l l 3 joint position sensors: 3 joint torque sensors: 3 motor position/speed sensors: 1 six-dimensional finger tip force torque sensor: 3 motor temperature sensors: 3 sensors for temperature compensation: integrated sensors